メネラウスの定理とチェバの定理の一般化
筆者は教科書や講義などで正式に射影幾何学を学んだことはありません。
論証・論理が不十分・不正確である可能性があるのでご留意ください。
前書き
メネラウスの定理とチェバの定理の双対性について書かれているwebサイトや書き込みを以前にいくつか見たことがあります。その中には二つの定理が双対であると書かれているものもありましたがそれは正確ではないと思います。それぞれの定理に現れる図形が双対の関係(に近い)というだけで、メネラウスの定理とチェバの定理が双対というわけではないということです。
双対は射影幾何で取り扱われるものです。メネラウスの定理やチェバの定理はユークリッド幾何を含むアフィン幾何の定理なのでそのままでは双対定理を考えることはできません。
そこで、この記事では、メネラウスの定理とチェバの定理を射影幾何の範疇へ一般化したうえで、それらの双対定理を考えてみようと思います。
定理の簡単なまとめ
最初にこの記事で紹介する定理の簡略版を図でおいておきます。複比を角括弧で表します。
 定理1
定理1
 定理2の系1
定理2の系1
 定理3
定理3
 定理4の系2
定理4の系2
実際のところ、以上の図がこの記事のほぼすべてです。
これらは通常のメネラウスの定理とチェバの定理を使えばユークリッド平面(あるいはアフィン平面)ではほぼ明らかですが、射影平面でも成り立つところにこの一般化の意味があると私は思います。
以下の本文では逆も成り立つことを示すためにわざと回りくどく書いています。
この記事について
この記事では、「複比」「斉次座標」「共線条件・共点条件」などの平面の射影幾何の基本事項は既知のものとして特に説明せず使います。
この記事は原則として射影平面で考えます。
(ユークリッド平面は無限遠点の集合[無限遠直線]を付け加えて射影平面になるようにすることができます。)
1直線上にある4点$P,Q,R,S$の複比($P,Q$に関する$R,S$の複比)を$[P,Q;R,S]$と書くことにします。
1点を通る4直線$k,l,m,n$の複比($k,l$に関する$m,n$の複比)を$[k,l;m,n]$と書くことにします。
基準となる三角形を$\triangle ABC$とし、基準点が$A(1,0,0),B(0,1,0),C(0,0,1)$となるように斉次座標系を設定します。(斉次座標系の単位点は任意に決めて構いません。)
この記事においてユークリッド平面における符号付き長さの比は$\overrightarrow{AP}$と$\overrightarrow{BP}$が同じ向きのときに正としています。$\overrightarrow{AP}$と$\overrightarrow{PB}$の向きで符号を決める場合は正負が逆になるので注意してください。
一般化されたメネラウスの定理とその双対定理
メネラウスの定理の射影平面への一般化
メネラウスの定理を射影平面で使える形に一般化することを考えます。
まず、射影平面では長さは定義されないため複比に置き換えます。ユークリッド平面において、一直線上にある3点が作る2つの有向線分の符号付きの長さの比は、その直線上にある無限遠点を含めた4点の複比に一致することを利用します。
また、純粋な射影幾何では無限遠直線を特別視する必要もないため、一般の直線で考えます。
すると、次のような一般化が考えられます。
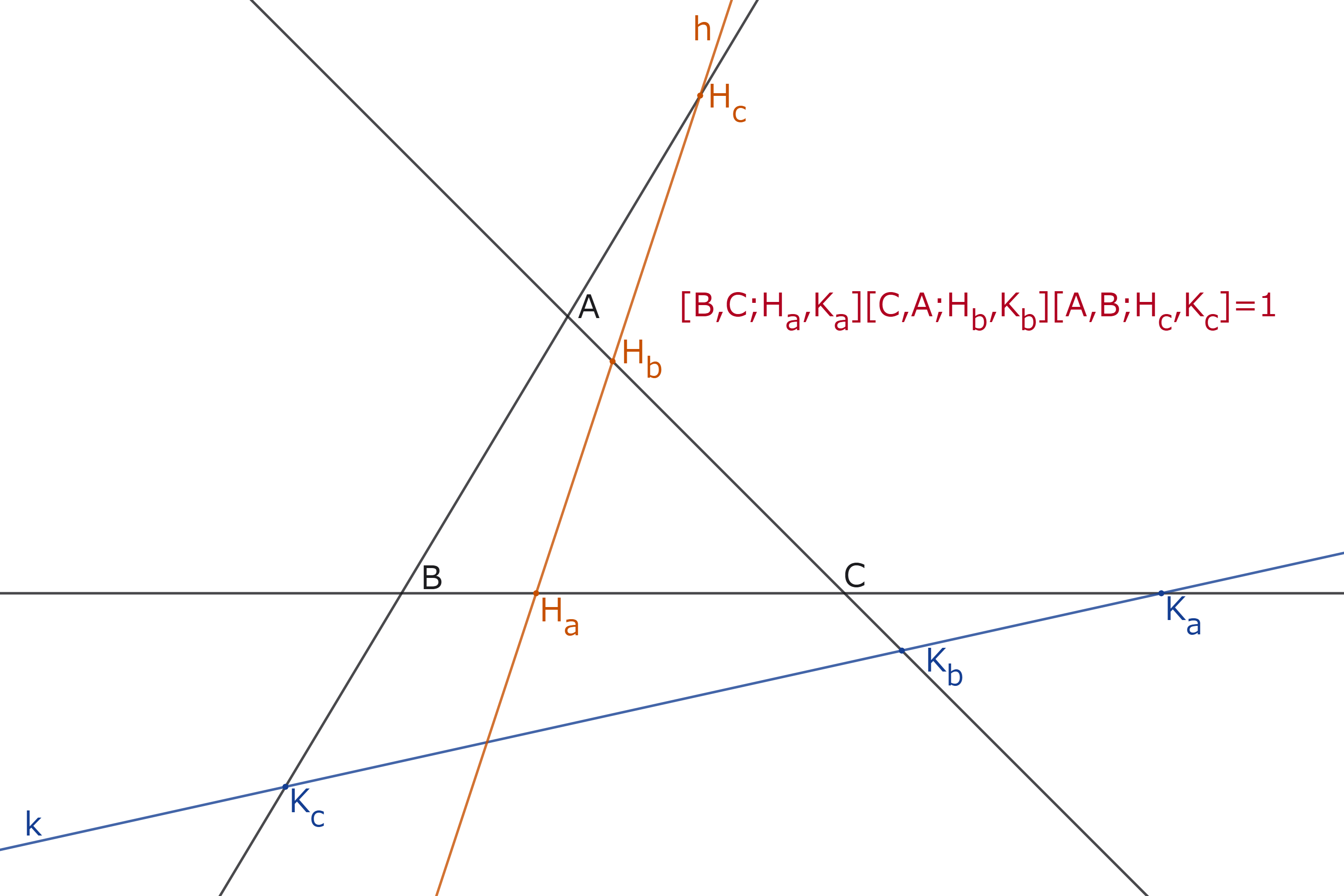
射影平面上に$\triangle ABC$があり、点$A,B,C$を通らない直線$k$がある。
直線$k$と直線$BC,CA,AB$の交点をそれぞれ$K_a,K_b,K_c$とおく。
直線$BC$上に点$B,C$と異なる点$P$があり、直線$CA$上に点$C,A$と異なる点$Q$があり、直線$AB$上に点$A,B$と異なる点$R$がある。
このとき、次の[i],[ii]は同値である。
- 3点$P,Q,R$が一直線上にある。
- $[B,C;P,K_a][C,A;Q,K_b][A,B;R,K_c]=1$
 定理1
定理1
ユークリッド平面の場合、tmにおける直線$k$として無限遠直線を選ぶと、[ii]に現れる複比が符号付き長さ比になるので通常のメネラウスの定理が得られます。
ユークリッド平面においては、[ii]の式が2つのメネラウスの定理の式を辺々割ったものになっているので証明は容易です。
以下では射影平面における証明を(2通りの方法で)行います。
直線$QR$と$BC$の交点を$P'$とすると、条件[i]は次のようになる。
- 3点$P,Q,R$が一直線上にある。
$\Leftrightarrow\ P$と$P'$が一致する。
$\Leftrightarrow\ [B,C;P,K_a]=[B,C;P',K_a]$
以下、直線$k,BC,QR$が一点で交わるかどうかで場合分けする。
◇直線$k,BC,QR$が一点で交わるとき。
このとき$K_a$と$P'$が一致するので$\,[B,C;P',K_a]=1\,$である。…①
また、$K_a$を中心とする配景写像を考えると$\,[A,B;R,K_c]=[A,C;Q,K_b]\,$が成り立つ。…②
ここで複比の性質より$\,\displaystyle [A,C;Q,K_b]=\frac{1}{[C,A;Q,K_b]}\,$なので、②は
$\,[C,A;Q,K_b][A,B;R,K_c]=1\,$となる。…②'
①,②'より、条件[ii]は次のようになる。
\begin{align}
\quad&\ [B,C;P,K_a][C,A;Q,K_b][A,B;R,K_c]=1 \\
&\Leftrightarrow\ [B,C;P,K_a]=1 \\
&\Leftrightarrow\ [B,C;P,K_a]=[B,C;P',K_a]
\end{align}
◇直線$k,BC,QR$が一点で交わらないとき。
直線$k$と$QR$の交点を$O$とし、直線$OA$と$BC$の交点を$S$とおく。
$O$を中心とする配景写像により$\,[C,A;Q,K_b]=[C,S;P',K_a]\,$および$\,[A,B;R,K_c]=[S,B;P',K_a]\,$が成り立つ。…③,④
また、一直線上にある5点が作る3つの複比に関する恒等式により、$[B,C;P',K_a][C,S;P',K_a][S,B;P',K_a]=1$となる。…⑤
③,④,⑤より、条件[ii]は次のようになる。
\begin{align}
\quad&\ [B,C;P,K_a][C,A;Q,K_b][A,B;R,K_c]=1 \\
&\Leftrightarrow\ [B,C;P,K_a][C,S;P',K_a][S,B;P',K_a]=1 \\
&\Leftrightarrow\ [B,C;P,K_a]\frac{1}{[B,C;P',K_a]}=1 \\
&\Leftrightarrow\ [B,C;P,K_a]=[B,C;P',K_a]
\end{align}
◇◇よって、直線$k,BC,QR$が一点で交わるときも一点で交わらないときも、条件[i]と[ii]は同値であることがわかった。
基準点が$A(1,0,0),B(0,1,0),C(0,0,1)$となる斉次座標系で考える。
直線$BC$の式は$\,x=0\,$,直線$CA$の式は$\,y=0\,$,直線$AB$の式は$\,z=0\,$となる。
直線$k$の式が$\,k_1x+k_2y+k_3z=0\,$であるとする。
直線$k$は点$A,B,C$を通らないので$\,k_1\neq0,\,k_2\neq0,\,k_3\neq0\,$である。
このとき、$K_a(0,k_3,-k_2),\,K_b(-k_3,0,k_1),\,K_c(k_2,-k_1,0)$となる。
点$P$は直線$BC$上にあるのでその座標は$(0,p_2,p_3)$と書ける。ただし$\,p_2\neq0,\,p_3\neq0\,$である。
点$Q$は直線$CA$上にあるのでその座標は$(q_1,0,q_3)$と書ける。ただし$\,q_1\neq0,\,q_3\neq0\,$である。
点$R$は直線$AB$上にあるのでその座標は$(r_1,r_2,0)$と書ける。ただし$\,r_1\neq0,\,r_2\neq0\,$である。
斉次座標による複比の計算により、
$\displaystyle [B,C;P,K_a]=\frac{p_3}{p_2}\cdot\frac{k_3}{-k_2},\quad[C,A;Q,K_b]=\frac{q_1}{q_3}\cdot\frac{k_1}{-k_3},\quad[A,B;R,K_c]=\frac{r_2}{r_1}\cdot\frac{k_2}{-k_1}$
となる。
ここで[i][ii]の条件を考えると次のようになる。
- 3点$P,Q,R$が一直線上にある。
$\Leftrightarrow\ \mdet{0&q_1&r_1\\p_2&0&r_2\\p_3&q_3&0}=0$
$\Leftrightarrow\ p_2q_3r_1+p_3q_1r_2=0$ - $[B,C;P,K_a][C,A;Q,K_b][A,B;R,K_c]=1$
$\Leftrightarrow\ \displaystyle \frac{p_3}{p_2}\cdot\frac{k_3}{-k_2}\cdot\frac{q_1}{q_3}\cdot\frac{k_1}{-k_3}\cdot\frac{r_2}{r_1}\cdot\frac{k_2}{-k_1}=1$
$\Leftrightarrow\ p_2q_3r_1+p_3q_1r_2=0$
よって[i]と[ii]は同値である。
tmの双対
射影平面で成り立つ定理が得られたので、その双対定理も成り立ちます。
射影平面上に$\triangle ABC$があり、直線$BC,CA,AB$上にない点$D$がある。
点$A$を通り$AC,AB$と異なる直線$l$があり、点$B$を通り$BA,BC$と異なる直線$m$があり、点$C$を通り$CB,CA$と異なる直線$n$がある。
このとき、次の[i],[ii]は同値である。
- 3直線$l,m,n$が一点で交わる。
- $[AC,AB;l,AD][BA,BC;m,BD][CB,CA;n,CD]=1$
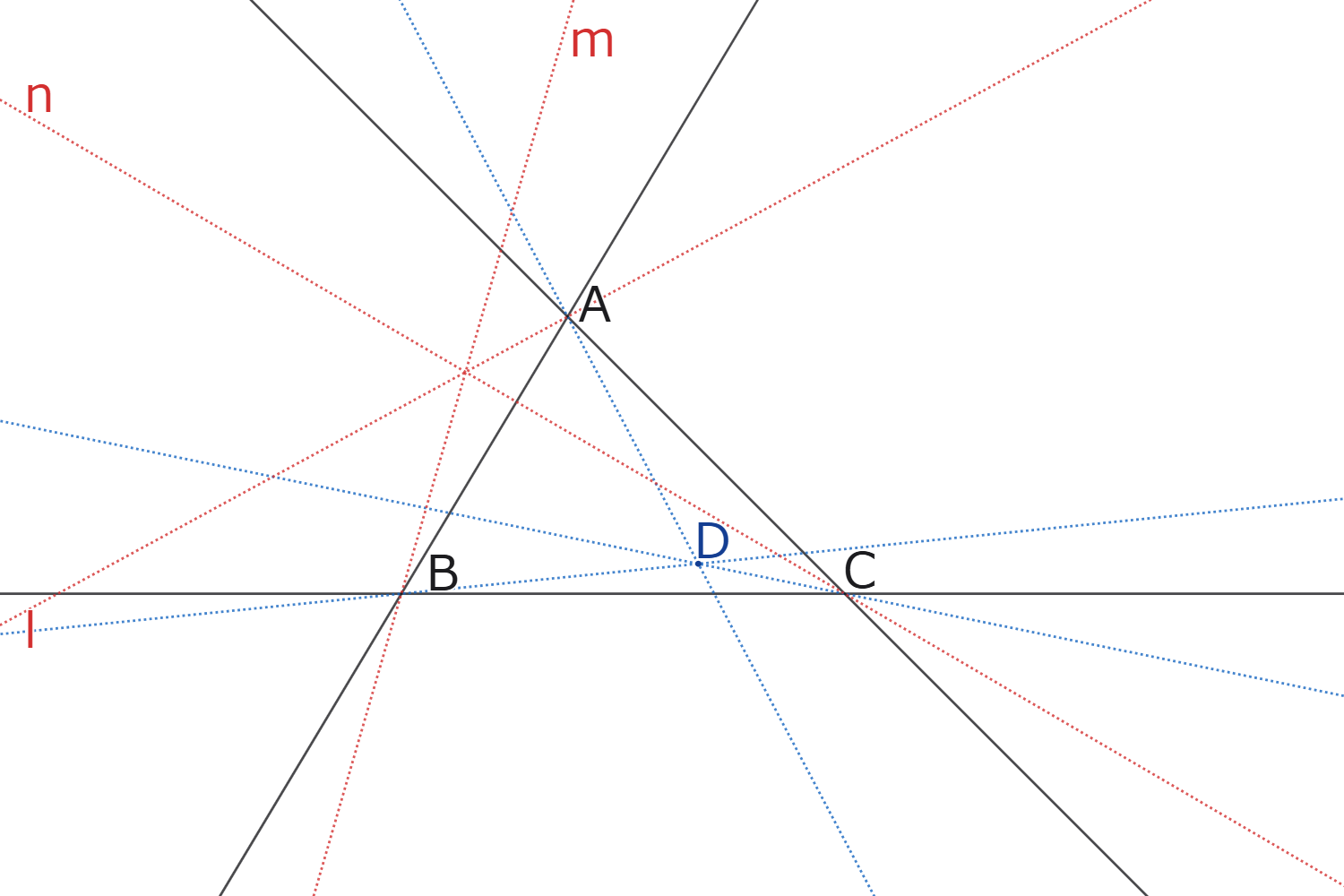 定理2
定理2
tmの双対なので、双対原理により真である。
注:双対であることがわかりにくいという方は次の囲みに書いたdtmの別表現とtmを比べてみてください。
射影平面上に3直線$a,b,c$を辺とする三角形があり、直線$a,b,c$上にない点$D$がある。
直線$b,c$の交点と点$D$を結ぶ直線を$d_a$,直線$c,a$の交点と点$D$を結ぶ直線を$d_b$,直線$a,b$の交点と点$D$を結ぶ直線を$d_c$とおく。
直線$b,c$の交点を通り$b,c$と異なる直線$l$があり、直線$c,a$の交点を通り$c,a$と異なる直線$m$があり、直線$a,b$の交点を通り$a,b$と異なる直線$n$がある。
このとき、次の[i],[ii]は同値である。
- 3直線$l,m,n$が一点で交わる。
- $[b,c;l,d_a][c,a;m,d_b][a,b;n,d_c]=1$
また、dtmがいえると次の系が簡単に示せます。
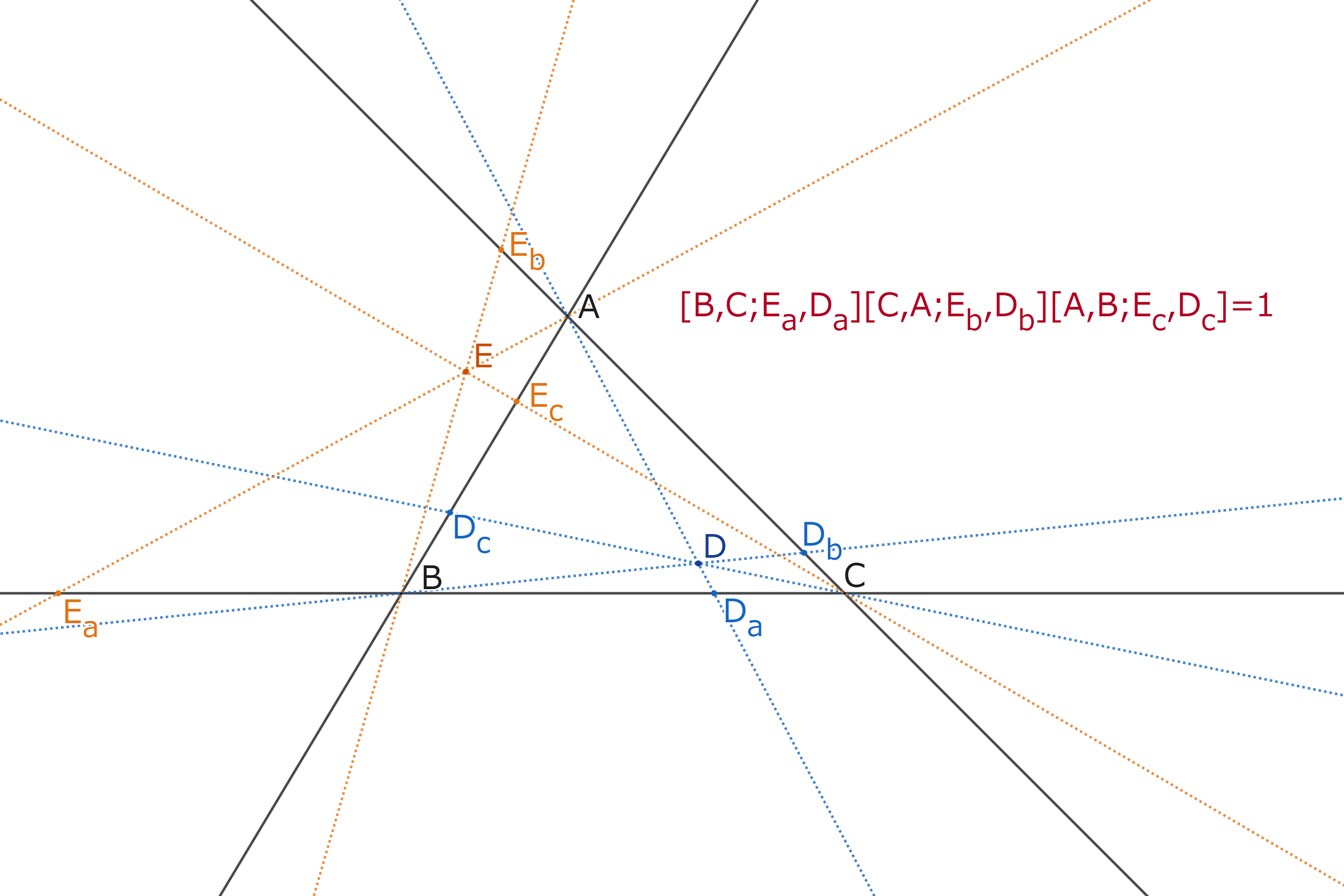
射影平面上に$\triangle ABC$があり、直線$BC,CA,AB$上にない点$D$がある。
直線$AD,BC$の交点を$D_a$,直線$BD,CA$の交点を$D_b$,直線$CD,AB$の交点を$D_c$とする。
直線$BC$上に点$B,C$と異なる点$P$があり、直線$CA$上に点$C,A$と異なる点$Q$があり、直線$AB$上に点$A,B$と異なる点$R$がある。
このとき、次の[i],[ii],[iii]は同値である。
- 3直線$AP,BQ,CR$が一点で交わる。
- $[AC,AB;AP,AD][BA,BC;BQ,BD][CB,CA;CR,CD]=1$
- $[B,C;P,D_a][C,A;Q,D_b][A,B;R,D_c]=1$
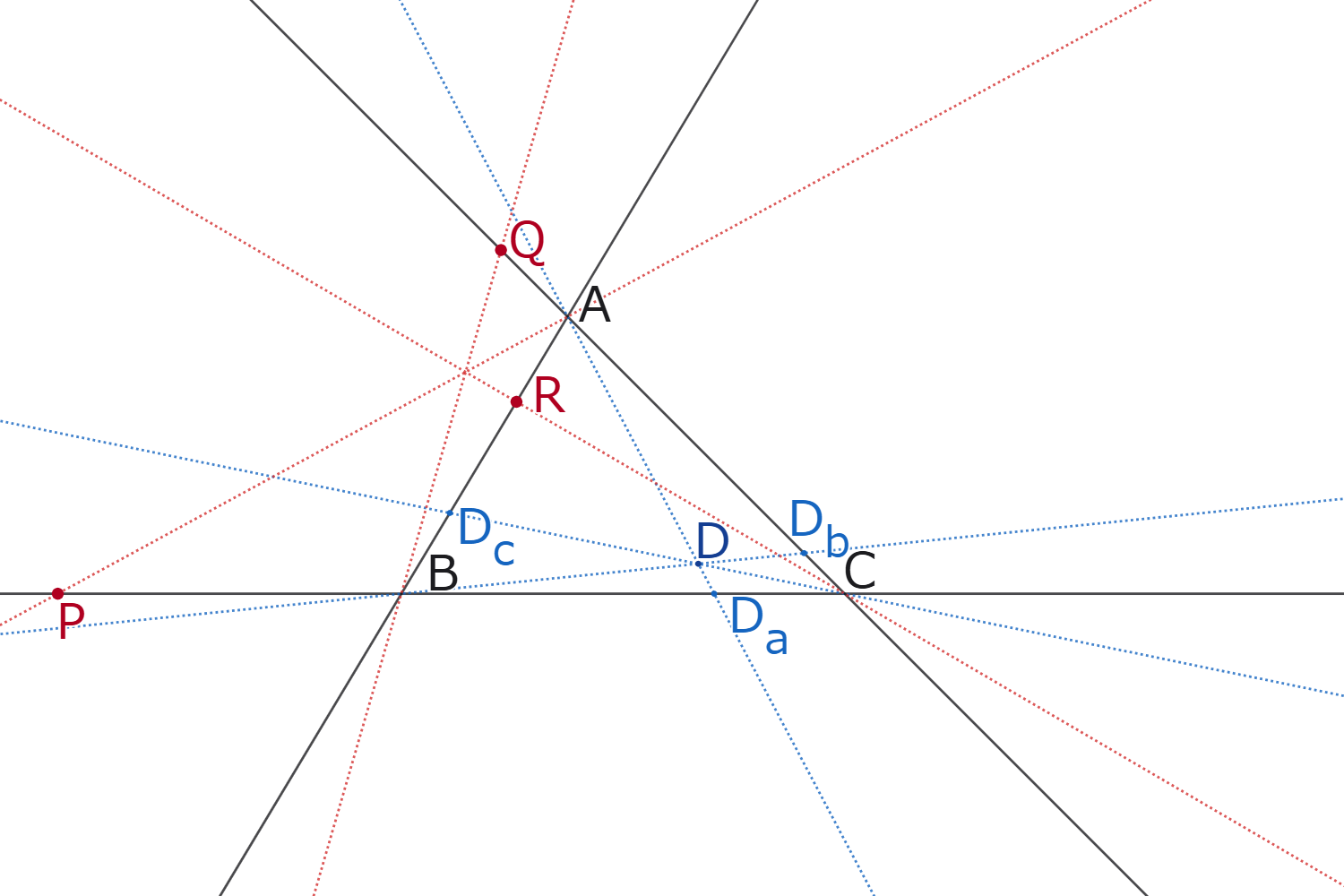 定理2 系1
定理2 系1
ユークリッド平面においては、[iii]の式が2つのチェバの定理の式を辺々割ったものになっています。
dtmにおける直線$l,m,n$をそれぞれ$AP,BQ,CR$にすれば[i]と[ii]が同値であることがわかる。
また、
$\displaystyle [AC,AB;AP,AD]=[AC,AB;AP,AD_a]=[C,B;P,D_a]=\frac{1}{[B,C;P,D_a]}$
であり、同様に
$\displaystyle [BA,BC;BQ,BD]=\frac{1}{[C,A;Q,D_b]},\quad [CB,CA;CR,CD]=\frac{1}{[A,B;R,D_c]}$
であるので、[ii]の式の両辺の逆数を取ることにより[iii]と同値であることがわかる。
ユークリッド平面の場合、定理2系1における点$D$として$\triangle ABC$の重心を選ぶと、$D_a,D_b,D_c$が各辺の中点となり[iii]に現れる複比が符号付き長さ比を$-1$倍したものになるので、通常のチェバの定理が得られます。
一般化されたチェバの定理とその双対定理
チェバの定理の射影平面への一般化
チェバの定理を射影平面で使える形に一般化することを考えます。
まず、射影平面では長さは定義されないため複比に置き換えます。ユークリッド平面において、一直線上にある3点が作る2つの有向線分の符号付きの長さの比は、その直線上にある無限遠点を含めた4点の複比に一致することを利用します。
また、純粋な射影幾何では無限遠直線を特別視する必要もないため、一般の直線で考えます。
すると、次のような一般化が考えられます。
射影平面上に$\triangle ABC$があり、点$A,B,C$を通らない直線$k$がある。
直線$k$と直線$BC,CA,AB$の交点をそれぞれ$K_a,K_b,K_c$とおく。
直線$BC$上に点$B,C$と異なる点$P$があり、直線$CA$上に点$C,A$と異なる点$Q$があり、直線$AB$上に点$A,B$と異なる点$R$がある。
このとき、次の[i],[ii]は同値である。
- 3直線$AP,BQ,CR$が一点で交わる。
- $[B,C;P,K_a][C,A;Q,K_b][A,B;R,K_c]=-1$
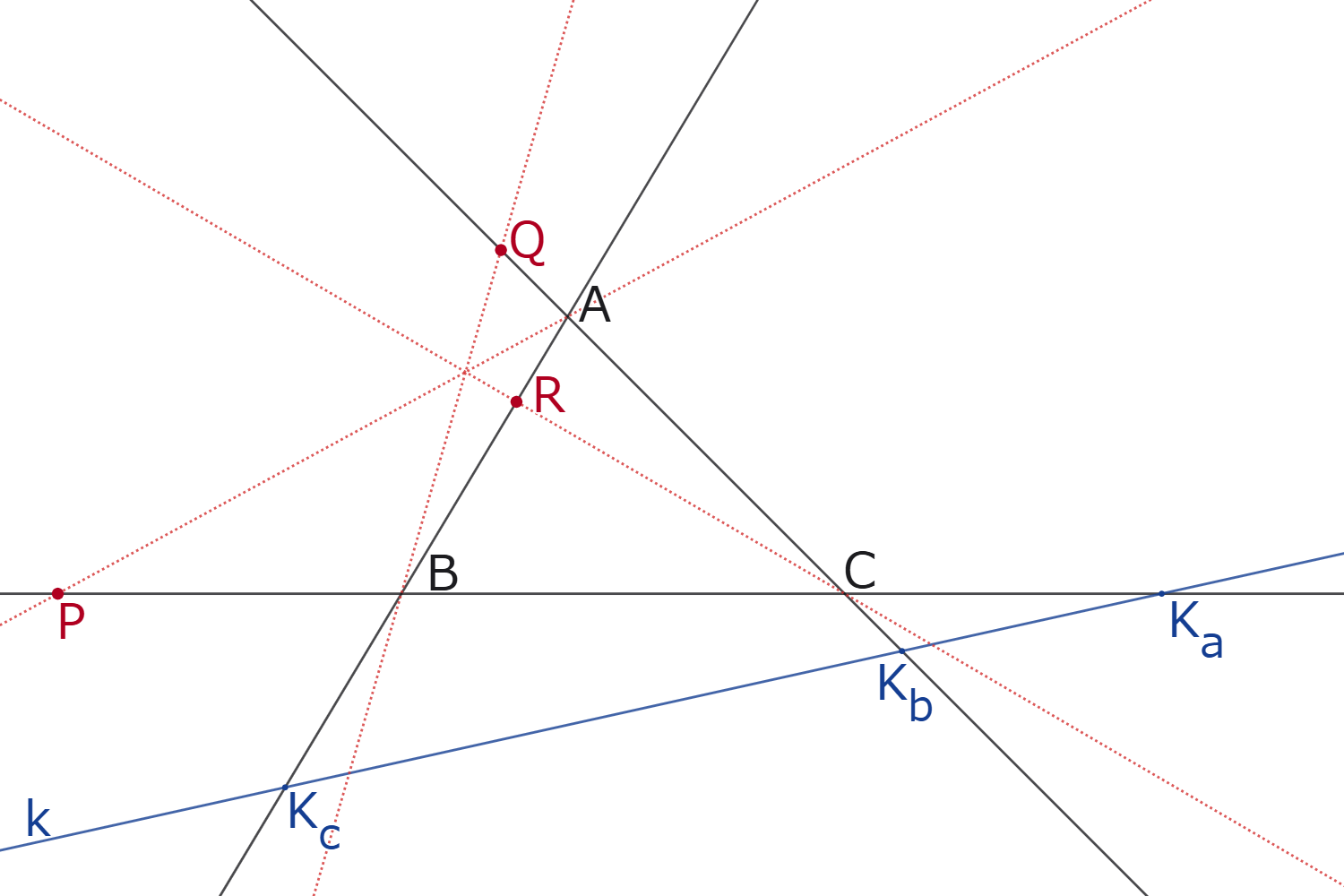 定理3
定理3
ユークリッド平面の場合、tcにおける直線$k$として無限遠直線を選ぶと、[ii]に現れる複比が符号付き長さ比になるので通常のチェバの定理が得られます。
ユークリッド平面においては、[ii]の式がチェバの定理の式とメネラウスの定理の式を辺々割ったものになっているので証明は容易です。
以下では射影平面における証明を(2通りの方法で)行います。
直線$BQ$と$CR$の交点を$T$とし、直線$AT$と$BC,QR$の交点をそれぞれ$P^*,U$とする。
また、直線$QR$と$BC$の交点を$P'$とする。
$T$を中心とする配景写像を考えると$\,[B,C,P^*,P']=[Q,R;U,P']\,$が成り立つ。…Ⅰ
$A$を中心とする配景写像を考えると$\,[B,C,P^*,P']=[R,Q;U,P']\,$が成り立つ。…Ⅱ
複比の性質より$\,[Q,R;U,P'][R,Q;U,P']=1\,$なので、Ⅰ,Ⅱの辺々を掛け合わせると
$\,[B,C,P^*,P']^2=1\,$となる。
ここで、$P'$と$P^*$が一致することはないので$\,[B,C,P^*,P']\neq1\,$より$\,[B,C,P^*,P']=-1\,$である。…Ⅲ
次に、一直線上にある5点が作る3つの複比に関する恒等式により$[B,C,P^*,P'][B,C;P',K_a][B,C;K_a,P^*]=1$である。…Ⅳ
また、複比の性質より$[B,C;P^*,K_a][B,C;K_a,P^*]=1$となる。…Ⅴ
Ⅲ,Ⅳ,Ⅴより、$[B,C;P^*,K_a]=-[B,C;P',K_a]$が成り立つ。…Ⅵ
Ⅵより、条件[i]は次のようになる。
- 3直線$AP,BQ,CR$が一点で交わる。
$\Leftrightarrow\ AP$と$AP^*$が一致する。
$\Leftrightarrow\ P$と$P^*$が一致する。
$\Leftrightarrow\ [B,C;P,K_a]=[B,C;P^*,K_a]$
$\Leftrightarrow\ [B,C;P,K_a]=-[B,C;P',K_a]$
以下、直線$k,BC,QR$が一点で交わるかどうかで場合分けする。
◇直線$k,BC,QR$が一点で交わるとき。
このとき$K_a$と$P'$が一致するので$\,[B,C;P',K_a]=1\,$である。…①
また、$K_a$を中心とする配景写像を考えると$\,[A,B;R,K_c]=[A,C;Q,K_b]\,$が成り立つ。…②
ここで複比の性質より$\,\displaystyle [A,C;Q,K_b]=\frac{1}{[C,A;Q,K_b]}\,$なので、②は
$\,[C,A;Q,K_b][A,B;R,K_c]=1\,$となる。…②'
①,②'より、条件[ii]は次のようになる。
\begin{align}
\quad&\ [B,C;P,K_a][C,A;Q,K_b][A,B;R,K_c]=-1 \\
&\Leftrightarrow\ [B,C;P,K_a]=-1 \\
&\Leftrightarrow\ [B,C;P,K_a]=-[B,C;P',K_a]
\end{align}
◇直線$k,BC,QR$が一点で交わらないとき。
直線$k$と$QR$の交点を$O$とし、直線$OA$と$BC$の交点を$S$とおく。
$O$を中心とする配景写像により$\,[C,A;Q,K_b]=[C,S;P',K_a]\,$および$\,[A,B;R,K_c]=[S,B;P',K_a]\,$が成り立つ。…③,④
また、一直線上にある5点が作る3つの複比に関する恒等式により、$[B,C;P',K_a][C,S;P',K_a][S,B;P',K_a]=1$となる。…⑤
③,④,⑤より、条件[ii]は次のようになる。
\begin{align}
\quad&\ [B,C;P,K_a][C,A;Q,K_b][A,B;R,K_c]=-1 \\
&\Leftrightarrow\ [B,C;P,K_a][C,S;P',K_a][S,B;P',K_a]=-1 \\
&\Leftrightarrow\ [B,C;P,K_a]\frac{1}{[B,C;P',K_a]}=-1 \\
&\Leftrightarrow\ [B,C;P,K_a]=-[B,C;P',K_a]
\end{align}
◇◇よって、直線$k,BC,QR$が一点で交わるときも一点で交わらないときも、条件[i]と[ii]は同値であることがわかった。
基準点が$A(1,0,0),B(0,1,0),C(0,0,1)$となる斉次座標系で考える。
直線$BC$の式は$\,x=0\,$,直線$CA$の式は$\,y=0\,$,直線$AB$の式は$\,z=0\,$となる。
直線$k$の式が$\,k_1x+k_2y+k_3z=0\,$であるとする。
直線$k$は点$A,B,C$を通らないので$\,k_1\neq0,\,k_2\neq0,\,k_3\neq0\,$である。
このとき、$K_a(0,k_3,-k_2),\,K_b(-k_3,0,k_1),\,K_c(k_2,-k_1,0)$となる。
点$P$は直線$BC$上にあるのでその座標は$(0,p_2,p_3)$と書ける。ただし$\,p_2\neq0,\,p_3\neq0\,$である。
点$Q$は直線$CA$上にあるのでその座標は$(q_1,0,q_3)$と書ける。ただし$\,q_1\neq0,\,q_3\neq0\,$である。
点$R$は直線$AB$上にあるのでその座標は$(r_1,r_2,0)$と書ける。ただし$\,r_1\neq0,\,r_2\neq0\,$である。
直線$AP$の式は$\,p_3y-p_2z=0\,$となり、直線$BQ$の式は$\,q_1z-q_3x=0\,$となり、直線$CR$の式は$\,r_2x-r_1y=0\,$となる。
斉次座標による複比の計算により、
$\displaystyle [B,C;P,K_a]=\frac{p_3}{p_2}\cdot\frac{k_3}{-k_2},\quad[C,A;Q,K_b]=\frac{q_1}{q_3}\cdot\frac{k_1}{-k_3},\quad[A,B;R,K_c]=\frac{r_2}{r_1}\cdot\frac{k_2}{-k_1}$
となる。
ここで[i][ii]の条件を考えると次のようになる。
- 3直線$AP,BQ,CR$が一点で交わる。
$\Leftrightarrow\ \mdet{0&p_3&-p_2\\-q_3&0&q_1\\r_2&-r_1&0}=0$
$\Leftrightarrow\ -p_2q_3r_1+p_3q_1r_2=0$ - $[B,C;P,K_a][C,A;Q,K_b][A,B;R,K_c]=-1$
$\Leftrightarrow\ \displaystyle \frac{p_3}{p_2}\cdot\frac{k_3}{-k_2}\cdot\frac{q_1}{q_3}\cdot\frac{k_1}{-k_3}\cdot\frac{r_2}{r_1}\cdot\frac{k_2}{-k_1}=-1$
$\Leftrightarrow\ -p_2q_3r_1+p_3q_1r_2=0$
よって[i]と[ii]は同値である。
tcの双対
射影平面で成り立つ定理が得られたので、その双対定理も成り立ちます。
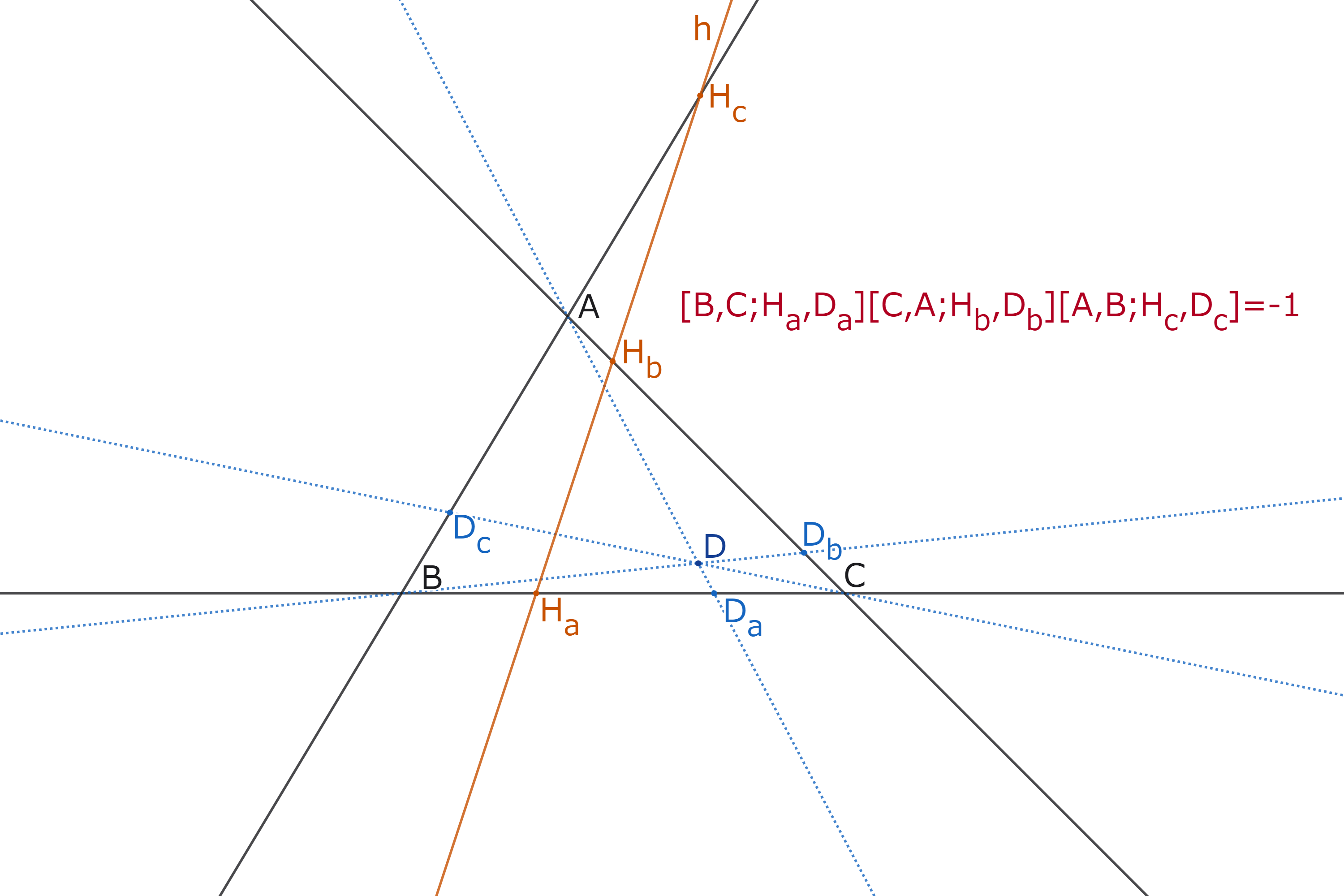
射影平面上に$\triangle ABC$があり、直線$BC,CA,AB$上にない点$D$がある。
点$A$を通り$AC,AB$と異なる直線$l$があり、点$B$を通り$BA,BC$と異なる直線$m$があり、点$C$を通り$CB,CA$と異なる直線$n$がある。
このとき、次の[i],[ii]は同値である。
- $l$と$BC$の交点,$m$と$CA$の交点,$n$と$AB$の交点が一直線上にある。
- $[AC,AB;l,AD][BA,BC;m,BD][CB,CA;n,CD]=-1$
 定理4
定理4
tcの双対なので、双対原理により真である。
注:双対であることがわかりにくいという方は次の囲みに書いたdtcの別表現とtcを比べてみてください。
射影平面上に3直線$a,b,c$を辺とする三角形があり、直線$a,b,c$上にない点$D$がある。
直線$b,c$の交点と点$D$を結ぶ直線を$d_a$,直線$c,a$の交点と点$D$を結ぶ直線を$d_b$,直線$a,b$の交点と点$D$を結ぶ直線を$d_c$とおく。
直線$b,c$の交点を通り$b,c$と異なる直線$l$があり、直線$c,a$の交点を通り$c,a$と異なる直線$m$があり、直線$a,b$の交点を通り$a,b$と異なる直線$n$がある。
このとき、次の[i],[ii]は同値である。
- $l$と$a$の交点,$m$と$b$の交点,$n$と$c$の交点が一直線上にある。
- $[b,c;l,d_a][c,a;m,d_b][a,b;n,d_c]=-1$
また、dtcがいえると次の系が簡単に示せます。
射影平面上に$\triangle ABC$があり、直線$BC,CA,AB$上にない点$D$がある。
直線$AD,BC$の交点を$D_a$,直線$BD,CA$の交点を$D_b$,直線$CD,AB$の交点を$D_c$とする。
直線$BC$上に点$B,C$と異なる点$P$があり、直線$CA$上に点$C,A$と異なる点$Q$があり、直線$AB$上に点$A,B$と異なる点$R$がある。
このとき、次の[i],[ii],[iii]は同値である。
- 3点$P,Q,R$が一直線上にある。
- $[AC,AB;AP,AD][BA,BC;BQ,BD][CB,CA;CR,CD]=-1$
- $[B,C;P,D_a][C,A;Q,D_b][A,B;R,D_c]=-1$
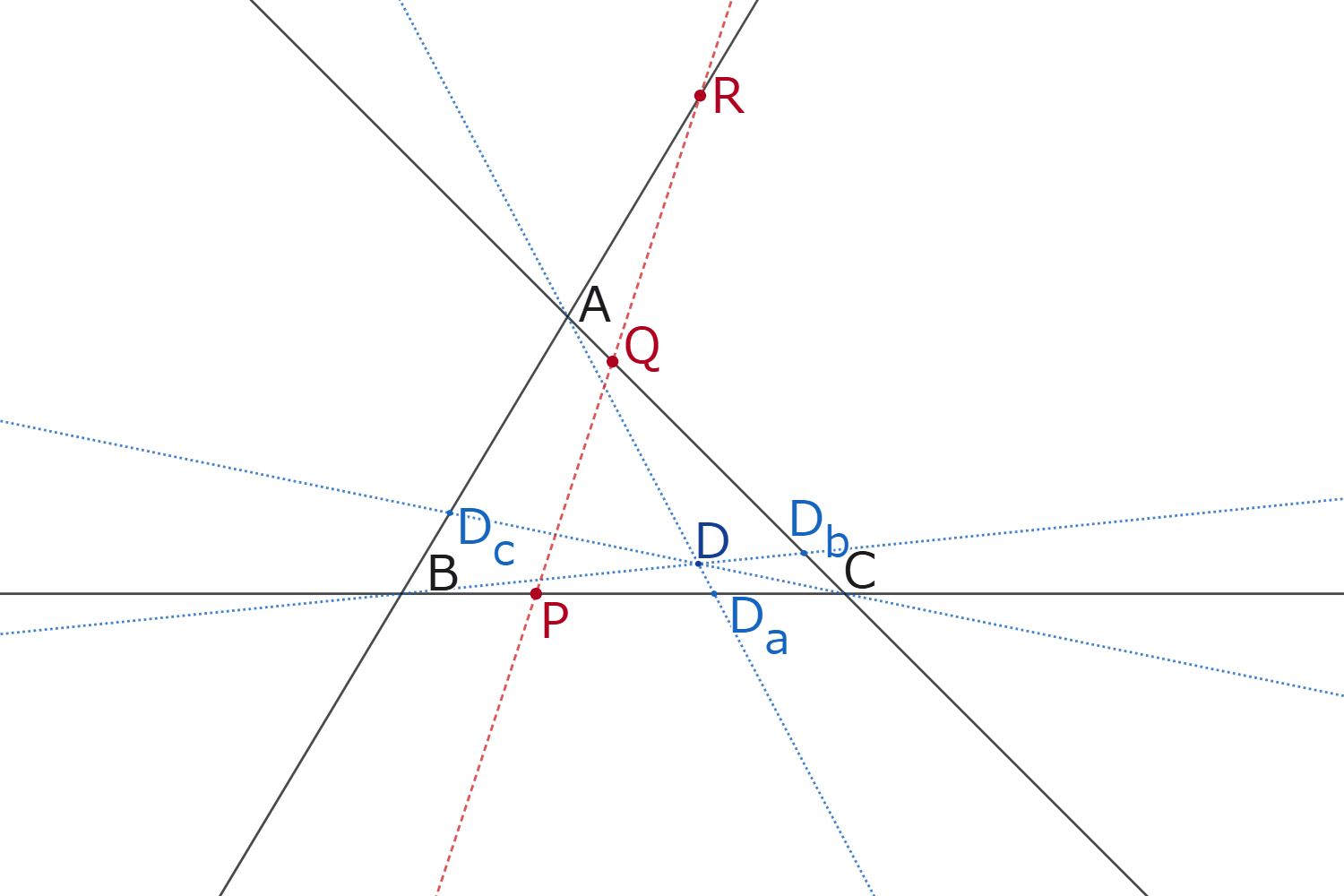 定理4 系2
定理4 系2
ユークリッド平面においては、[iii]の式がメネラウスの定理の式とチェバの定理の式を辺々割ったものになっています。
dtcにおける直線$l,m,n$をそれぞれ$AP,BQ,CR$にすれば[i]と[ii]が同値であることがわかる。
また、
$\displaystyle [AC,AB;AP,AD]=[AC,AB;AP,AD_a]=[C,B;P,D_a]=\frac{1}{[B,C;P,D_a]}$
であり、同様に
$\displaystyle [BA,BC;BQ,BD]=\frac{1}{[C,A;Q,D_b]},\quad [CB,CA;CR,CD]=\frac{1}{[A,B;R,D_c]}$
であるので、[ii]の式の両辺の逆数を取ることにより[iii]と同値であることがわかる。
ユークリッド平面の場合、定理4系2における点$D$として$\triangle ABC$の重心を選ぶと、$D_a,D_b,D_c$が各辺の中点となり[iii]に現れる複比が符号付き長さ比を$-1$倍したものになるので、通常のメネラウスの定理が得られます。
後書き
冒頭に置いた簡単なまとめの図はそれぞれの定理や系の[i]$\Rightarrow$[ii],[iii]を表しています。
その内容を言葉で簡単にまとめると次のようになります。
- 一般化されたメネラウスの定理およびその双対定理…「三角形と2直線」あるいは「三角形と2点」が与えられたときにできる3つの複比の積が「$+1$」になる。
- 一般化されたチェバの定理およびその双対定理…「三角形と1直線と1点」が与えられたときにできる3つの複比の積が「$-1$」になる。
この二つの間は、「三線極線・三線極点」の関係や「調和点列・調和線束」と複比に関する性質によって密接に関係しているのですが、私は簡潔に説明する自信がないので書くことはやめておきます。
(ただ、tcの証明その1の前半部分に二つの定理の関係性が多分に現れているので、そこを見れば何となくはつかめると思います。)