級数のweight減少に関するヒューリスティックな話

こんにちは、受験勉強を終えたitouです。ようやく好き放題数学ができるようになってMZVを勉強し始めました。
で、ネットを漁って数式を探してたらこんなのを見つけました。
Ozonumさんのポスト
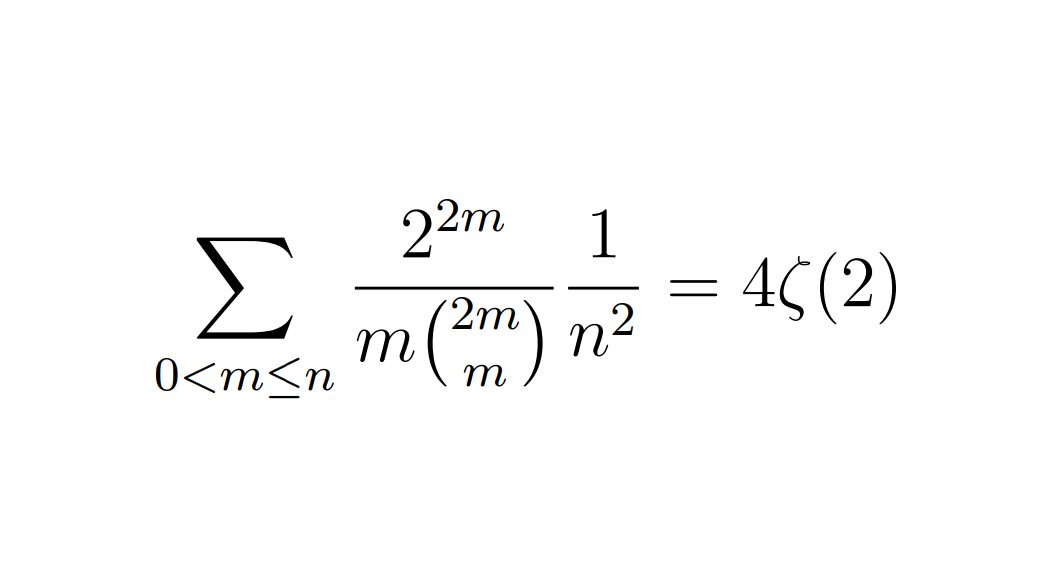数式１

Ozonumさんも言っていますが、左辺の級数のweightは3なのに、右辺は２です。つまりweightが下がってるわけですが、これはなぜでしょうか？

weightの概念の整理

そもそもweightとはMZVに対して定義される概念で、

\begin{multline} \zeta(\mathbf k):=\sum_{0< m_a< m_{a-1}<…< m_1}{\frac{1}{m_1^{k_{1}} m_2^{k_{2}}…m_a^{k_{a}}}} \end{multline}
（この記事ではインデックスは左向き）
における$wt=k_1+k_2+…+k_a$のことを指します。しかし、多くの場合MZV以外にもこの概念が通用するわけです。感覚的ですが、次のようなルールに則っているように思います。

ルール①$log(x)$や$\sqrt{x}$は$wt=1、\pi^n$は$wt=n$。
ルール②級数表示の中で、二項係数${ 2n \choose n }$や${ 3n \choose n }$、指数関数$2^{2n}$などは$wt=0$
ルール③級数表示の中で、分数次数が$-n$なら$wt=n$。複数のローカル変数について和を取る場合は、全次数$-n$として$wt=n$
ルール④指数法則同様、$wt=a,wt=b$の２つの数の積のweightは$a+b$

これらルールは多くの場合について成立します。たとえば アカデミック後進国ニッポンさんの記事 を見てください。

本題

唐突ですが、ある級数に対し、その有限和を考えます。まずＭＺＶに対しては多重調和和を
\begin{multline} \zeta_N(\mathbf k):=\sum_{0< m_a< m_{a-1}<…< m_1< N}{\frac{1}{m_1^{k_{1}} m_2^{k_{2}}…m_a^{k_{a}}}} \end{multline}
とし、
\begin{multline} \Delta a_n:=a_{n+1}-a_n \end{multline}
とします。

\begin{multline} \Delta \zeta_N(k:\mathbf k)=\frac{1}{N^k} \zeta_N(\mathbf k) \end{multline}
がすぐに分かります。特に、
\begin{multline} \Delta \zeta_N(k)=\frac{1}{N^k} \end{multline}
です。ここで、$ N^k\Delta \zeta_N(k)=1$より自明な漸化式、
\begin{multline} (N+1)^k\Delta \zeta_{N+1}(k)=N^k\Delta \zeta_N(k) \end{multline}
が従います。これより$\Delta\zeta_N(k_1,k_2)$は
\begin{multline} (N+1)^{k_2}\{(N+2)^{k_1}\Delta \zeta_{N+2}(k_1)-(N+1)^{k_1}\Delta \zeta_{N+1}(k_1)\}=N^{k_2}\{(N+1)^{k_1}\Delta \zeta_{N+1}(k_1)-N^{k_1}\Delta \zeta_{N}(k_1)\} \end{multline}

という３項間漸化式を満たします。つまり、$\zeta_N(k_1,k_2)$は４項間漸化式を満たします。同様に帰納的に、$\zeta_N(k_1,k_2,…k_n)$は$(n+2) $項間漸化式を満たします。また、各項には$(k_1+k_2+…k_n)$次の多項式がかけられています。

～～～～～ここからヒューリスティックな話～～～～～

$wt=k,dep=n$の多重調和和が$(n+2)$項間、各項に$(k_1+k_2+…k_n)$次の多項式が乗じられた漸化式を満たすなら、これを逆に、一般の級数に対してweightとdepthの定義とするのはどうでしょうか？つまり、

※$N$未満までで打ち切るとは、たとえば$0< m_1\leq m_2< m_3$を渡る級数なら、$0< m_1\leq m_2< m_3< N$での部分和を取ることです。

（例２は らららさん に教えてもらいました。weightの概念の整理の項で述べたルールではこの級数のweightは０ですが、この定義では１となります。）

weight減少のルール

この定義でうまくいくぞ！と思って冒頭の級数にも同じことをします。

\begin{multline} \sum_{0< m\leq n}\frac{1}{{ n^2 m\beta_m} }=4\zeta(2) \end{multline}
左辺の部分和を$S_N$として、
\begin{multline} \begin{split} \Delta S_N&=\frac{1}{N^2}\sum_{0< m\leq N}\frac{1}{m\beta_m}\\ \Delta N^2\Delta S_N&=\frac{1}{(N+1)\beta_{N+1}}\\ \end{split} \end{multline}
より、自明な漸化式$(N+\frac{3}{2})\Delta (N+1)^2 \Delta S_{N+1}=(N+1)\Delta N^2 \Delta S_{N}$
が従う。$\Delta N^2\Delta S_N=(N+1)^2(S_{N+2}-S_{N+1})-N^2(S_{N+1}-S_{N})$なので、weightは３、depthは２

…うまくいってない！

$wt=2$となってほしいのに、３になってしまいました。これを解消するために天下りですが、次のルールを導入します。

これがどこから出てきたのか説明します。

$\sum_{m>0}\frac{1}{(m)_a}=\frac{1}{(a-1)(a-1)!}(a\ne1)$を用意します。
部分和$S_N$は自明な漸化式$(N+a)\Delta S_{N+1}=N\Delta S_N$を満たします。この級数の右辺は有理数なので、これのweightは０としたいのです。また、多項式中の$N$と$\Delta S_N$の$N$はずれていてもいいので、$ (N+a+b)\Delta S_{N+1}=(N+b) \Delta S_{N}(a,b\in \mathbb{R} ,a\ne1)$に対応する級数のweightを０と定めます。そして、$\Delta $はweightには関係せず、$N$の$k$次多項式をかけるとweightが$k$下がる（これはMZVの例で確かめた）ことを適応したのです。

実際、このルールを導入すると、
冒頭の級数について
$(N+\frac{3}{2})\Delta (N+1)^2 \Delta S_{N+1}=(N+1)\Delta N^2 \Delta S_{N}$より$a=1/2,b=1$で$\Delta N^2 \Delta S_{N}$のweightが０で、$N^2$がかけられているので、$wt=2$となり、右辺のweightと一致します。

考察

漸化式を使ってweightの一般的定義を導入してみました。厳密な議論は全然ですが…今回導入したルール以外にもweightが減少する場合があるかもしれないので、今後はそのあたりが課題ですね。そもそも有限級数に漸化式を使おうという発想は、（もともとこういうタイプの漸化式に興味があったのですが）便利さんの例の論文をみて私も有限和関連の面白いことをしたいなあと思った所からです。

謝辞

ここまで読んで下さりありがとうございました。誤植誤り等指摘お願いします。

追記（2024/3/26）
・例１の級数が間違っていたので訂正
・以下の式（$k\geq 2$）についてはweight0とならない（weight減少は起こる）ので、成果が得られるまで削除
\begin{multline} (N+a+b)^kS'_{N+1}=(N+b)^k S'_{N}(a,b\in \mathbb{R} ,a\ne1) \end{multline}