Taylor展開の証明と例
Taylor展開（1変数）
証明
$I$を開区間，$g:I\to\mathbb{R}$を$C^{1}$級関数とする．
このとき，任意の$a,x\in I$に対して
$$ g(x)=g(a)+\int_{a}^{x}g'(t)\,dt$$
が成り立つ．
略．
$k$を正の整数，$I$を開区間，$f:I\to\mathbb{R}$を$C^{k}$級関数とする．
このとき，任意の$a,x\in I$に対して
$$ f(x)=\sum_{n=0}^{k-1}\frac{f^{(n)}(a)}{n!}(x-a)^{n}+\frac{(x-a)^k}{(k-1)!}\int_{0}^{1}(1-t)^{k-1}f^{(k)}(tx+(1-t)a)\,dt$$
が成り立つ．
次の関数$g:[0,1]\to\mathbb{R}$
$$ g(t):=(1-t)^{k-1}f^{(k-1)}(tx+(1-t)a) \qquad (t\in[0,1])$$
は$C^{1}$級（正確には，$[0,1]$を含むある開区間上の$C^{1}$級関数に拡張可能）であり
$$
g'(t)=
\begin{cases}
(x-a)f'(tx+(1-t)a) & (k=1), \\
-(k-1)(1-t)^{k-2}f^{(k-1)}(tx+(1-t)a)+(1-t)^{k-1}(x-a)f^{(k)}(tx+(1-t)a) & (k\ge 2)
\end{cases}
\qquad (t\in[0,1])$$
が成り立つ．
- $k=1$の場合，$g(0)=f(a)$と$g(1)=f(x)$に注意すれば，微分積分学の基本定理より
\begin{align*} f(x)&=g(1) \\ &=g(0)+\int_{0}^{1}g'(t)\,dt \\ &=f(a)+(x-a)\int_{0}^{1}f'(tx+(1-t)a)\,dt. \end{align*} - $k\ge 2$の場合，$g(0)=f^{(k-1)}(a)$と$g(1)=0$に注意すれば，微分積分学の基本定理と帰納法の仮定より
\begin{align*} f(x) &=\sum_{n=0}^{k-2}\frac{f^{(n)}(a)}{n!}(x-a)^{n}+\frac{(x-a)^{k-1}}{(k-2)!}\int_{0}^{1}(1-t)^{k-2}f^{(k-1)}(tx+(1-t)a)\,dt \\ &=\sum_{n=0}^{k-1}\frac{f^{(n)}(a)}{n!}(x-a)^{n}-\frac{f^{(k-1)}(a)}{(k-1)!}(x-a)^{k-1}+\frac{(x-a)^{k-1}}{(k-2)!}\int_{0}^{1}(1-t)^{k-2}f^{(k-1)}(tx+(1-t)a)\,dt \\ &=\sum_{n=0}^{k-1}\frac{f^{(n)}(a)}{n!}(x-a)^{n}+\frac{(x-a)^{k-1}}{(k-1)!}\bigg(g(1)-g(0)+\int_{0}^{1}(k-1)(1-t)^{k-2}f^{(k-1)}(tx+(1-t)a)\,dt\bigg) \\ &=\sum_{n=0}^{k-1}\frac{f^{(n)}(a)}{n!}(x-a)^{n}+\frac{(x-a)^{k-1}}{(k-1)!}\int_{0}^{1}\bigg(g'(t)+(k-1)(1-t)^{k-2}f^{(k-1)}(tx+(1-t)a)\bigg)\,dt \\ &=\sum_{n=0}^{k-1}\frac{f^{(n)}(a)}{n!}(x-a)^{n}+\frac{(x-a)^{k-1}}{(k-1)!}\int_{0}^{1}(1-t)^{k-1}(x-a)f^{(k)}(tx+(1-t)a)\,dt \\ &=\sum_{n=0}^{k-1}\frac{f^{(n)}(a)}{n!}(x-a)^{n}+\frac{(x-a)^{k}}{(k-1)!}\int_{0}^{1}(1-t)^{k-1}f^{(k)}(tx+(1-t)a)\,dt. \end{align*}
例１：指数関数
任意の正の整数$k$と$x\in\mathbb{R}$に対して
$$ \color{red} e^x=\sum_{n=0}^{k-1}\frac{1}{n!}x^{n}+\frac{x^k}{(k-1)!}\int_{0}^{1}(1-t)^{k-1}e^{tx}\,dt$$
が成り立つ．
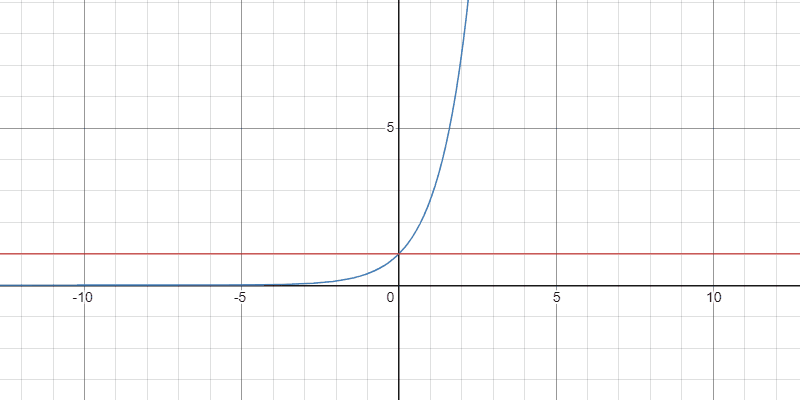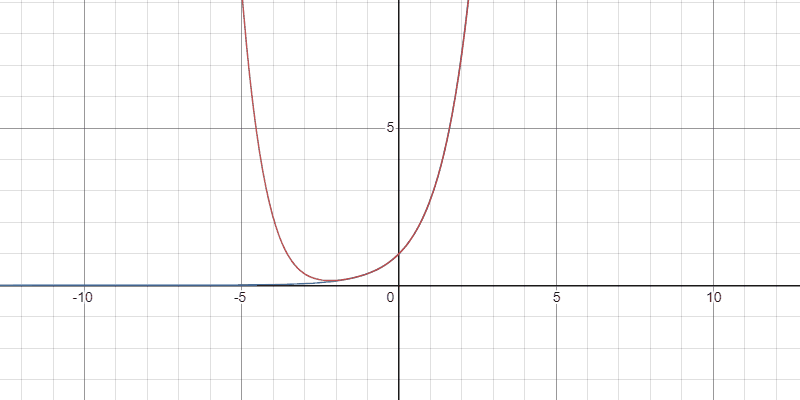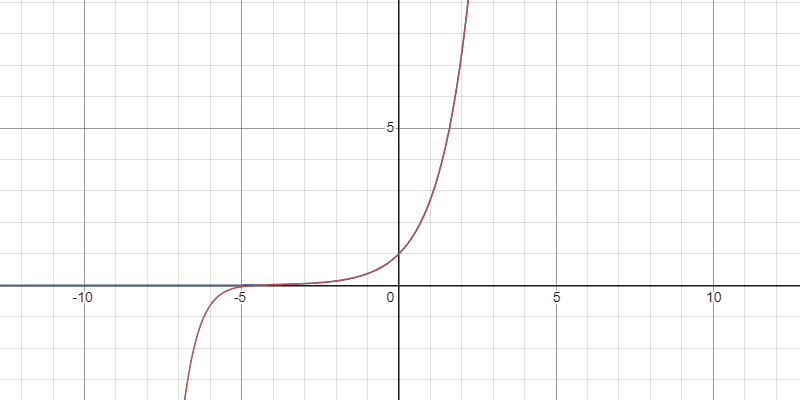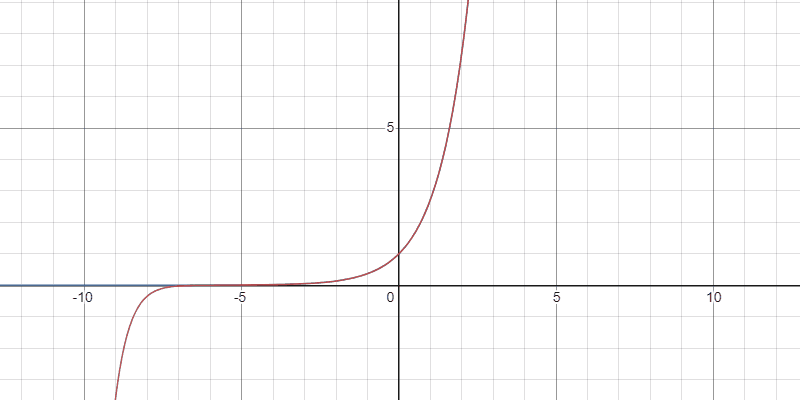Taylor多項式の収束の様子
- $x>0$のとき，任意の正の整数$k$に対して次式が成り立つ．
\begin{align*} e^{x}&< \sum_{n=0}^{k-1}\frac{1}{n!}x^{n}. \end{align*} - $x<0$のとき，任意の正の整数$\ell$に対して次式が成り立つ．
\begin{align*} \sum_{n=0}^{2\ell-1}\frac{1}{n!}x^{n}< e^{x}<\sum_{n=0}^{2\ell-2}\frac{1}{n!}x^{n}. \end{align*}
$$ \int_{0}^{1}(1-t)^{k-1}e^{tx}\,dt>0$$
が成り立つから，あとは$x^k$の符号を見ればよい．
任意の$x\in\mathbb{R}$に対して，次式が成り立つ：
\begin{align*}
e^{x}&=\sum_{n=0}^{\infty}\frac{1}{n!}x^{n}.
\end{align*}
$$ \bigg|\frac{x^k}{(k-1)!}\int_{0}^{1}(1-t)^{k-1}e^{tx}\,dt\bigg|\le \frac{|x|^k}{(k-1)!}e^{x}\to 0 \qquad (k\to\infty)$$
となる．
$e$は無理数である．
もし$e$が有理数であれば，互いに素な正の整数$k,\ell$を用いて$e=\ell/k$と表せる．このとき$e^x$のTaylor展開に$x=1$を代入した
\begin{align*}
e&=\sum_{n=0}^{k}\frac{1}{n!}+\frac{1}{k!}\int_{0}^{1}(1-t)^{k}e^{t}\,dt
\end{align*}
より
\begin{align*}
\int_{0}^{1}(1-t)^{k}e^{t}\,dt&=(k-1)!\ell-\sum_{n=0}^{k}\frac{k!}{n!}
\end{align*}
が成り立つ．この右辺が整数であるのに対して，左辺については
\begin{align*}
0<\int_{0}^{1}(1-t)^{k}e^{t}\,dt&\le \int_{0}^{1}(1-t)e^t\,dt=e-2<1
\end{align*}
となり整数でないから矛盾．
例２：余弦関数
任意の正の整数$k$と$x\in\mathbb{R}$に対して
$$ \color{red} \cos(x)=\sum_{n=0}^{k-1}\frac{(-1)^{n}}{(2n)!}x^{2n}+\frac{(-1)^{k}x^{2k-1}}{(2k-2)!}\int_{0}^{1}(1-t)^{2k-2}\sin(tx)\,dt$$
が成り立つ．
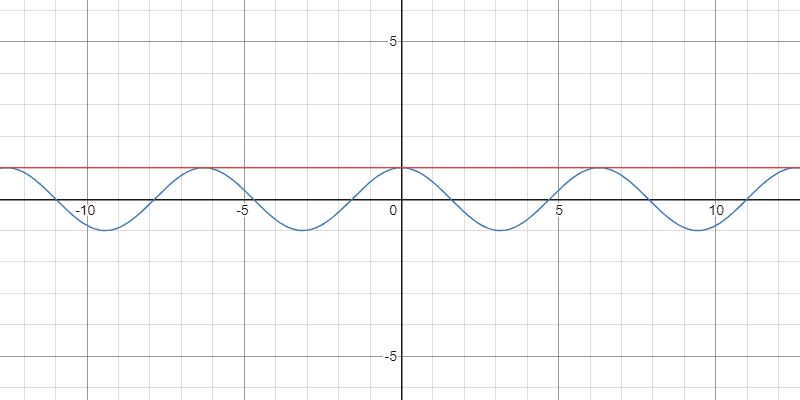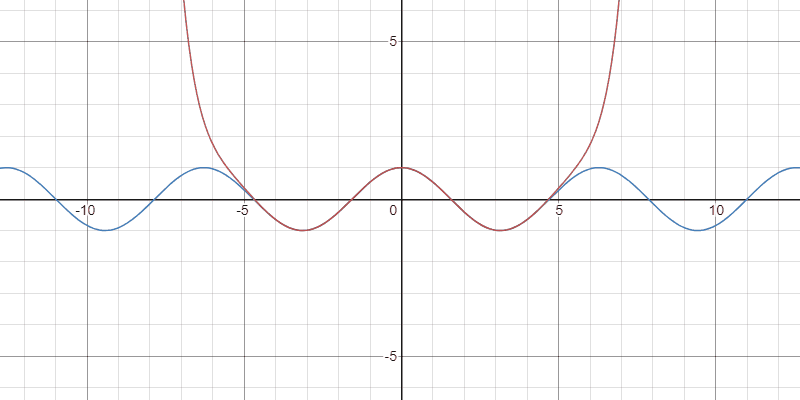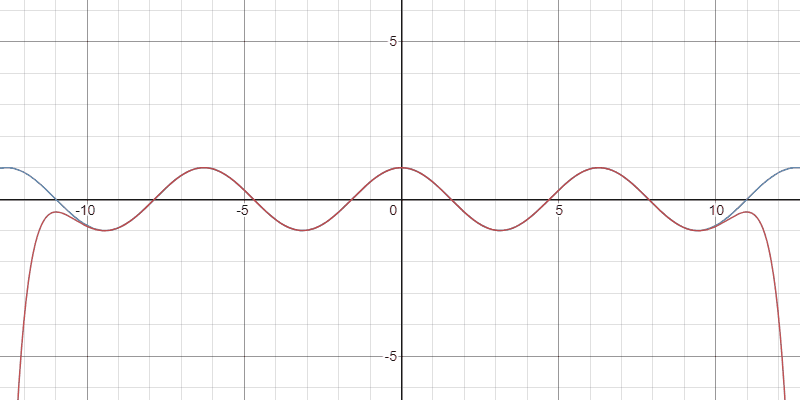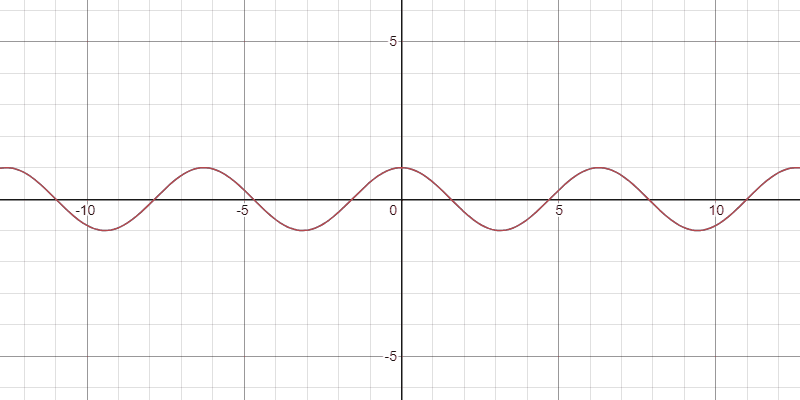Taylor多項式の収束の様子
$x>0$のとき，（関数$t\mapsto \sin(tx)$の周期の半分を）$L:=\pi/x$とおくと，任意の単調減少連続関数$g:\mathbb{R}\to[0,\infty)$と整数$m$に対して
\begin{align*}
\int_{(2m-2)L}^{2mL}g(t)\sin(tx)\,dt
&\ge0
\end{align*}
が成り立つ．
$\sin(tx)$の符号に注意して評価すると
\begin{align*}
\int_{(2m-2)L}^{2mL}g(t)\sin(tx)\,dt
&\ge \int_{(2m-2)L}^{(2m-1)L}g(t)\sin(tx)\,dt+\int_{(2m-1)L}^{2mL}g(t)\sin(tx)\,dt \\
&\ge\int_{(2m-2)L}^{(2m-1)L}g((2m-1)L)\sin(tx)\,dt+\int_{(2m-1)L}^{2mL}g((2m-1)L)\sin(tx)\,dt \\
&=g((2m-1)L)\int_{(2m-2)L}^{2mL}\sin(tx)\,dt \\
&=0.
\end{align*}
任意の正の整数$\ell$と$x\in\mathbb{R}$に対して，次式が成り立つ：
$$ \sum_{n=0}^{2\ell-1}\frac{(-1)^{n}}{(2n)!}x^{2n}\le\cos(x)\le\sum_{n=0}^{2\ell-2}\frac{(-1)^{n}}{(2n)!}x^{2n}.$$
任意の$x\in\mathbb{R}$に対して，次式が成り立つ：
\begin{align*}
\cos(x)&=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n)!}x^{2n}.
\end{align*}
$$ \bigg|\frac{(-1)^{k}x^{2k-1}}{(2k-2)!}\int_{0}^{1}(1-t)^{2k-2}\sin(tx)\,dt\bigg|\le \frac{|x|^{2k-1}}{(2k-2)!}\to 0 \qquad (k\to\infty)$$
となる．
$\cos(1)$は無理数である．
もし$\cos(1)$が有理数であれば，互いに素な正の整数$k,\ell$を用いて$\cos(1)=\ell/k$と表せる．このとき$\cos(x)$のTaylor展開に$x=1$を代入した
\begin{align*}
\cos(1)=\sum_{n=0}^{k}\frac{(-1)^{n}}{(2n)!}+\frac{(-1)^{k+1}}{(2k)!}\int_{0}^{1}(1-t)^{2k}\sin(t)\,dt
\end{align*}
より
\begin{align*}
\int_{0}^{1}(1-t)^{2k}\sin(t)\,dt&=(-1)^{k+1}\bigg(\frac{(2k)!\ell}{k}-\sum_{n=0}^{k}\frac{(2k)!(-1)^n}{(2n)!}\bigg)
\end{align*}
が成り立つ．この右辺が整数であるのに対して，左辺については
\begin{align*}
0<\int_{0}^{1}(1-t)^{2k}\sin(t)\,dt<1
\end{align*}
となり整数でないから矛盾．
例３：正弦関数
任意の正の整数$k$と$x\in\mathbb{R}$に対して
$$ \color{red} \sin(x)=\sum_{n=0}^{k-1}\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}+\frac{(-1)^{k}x^{2k}}{(2k-1)!}\int_{0}^{1}(1-t)^{2k-1}\sin(tx)\,dt$$
が成り立つ．
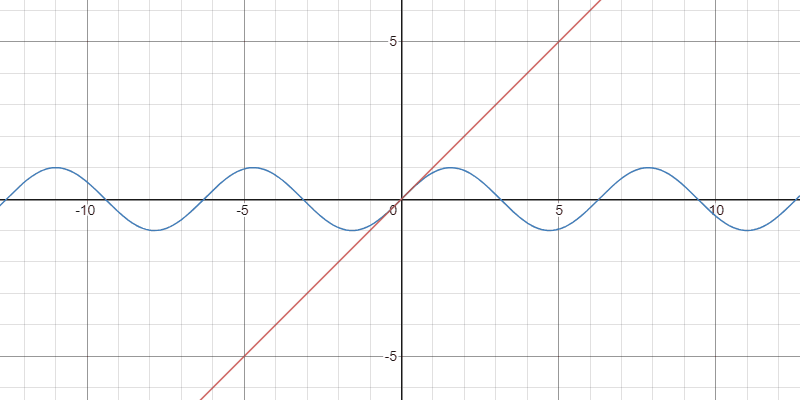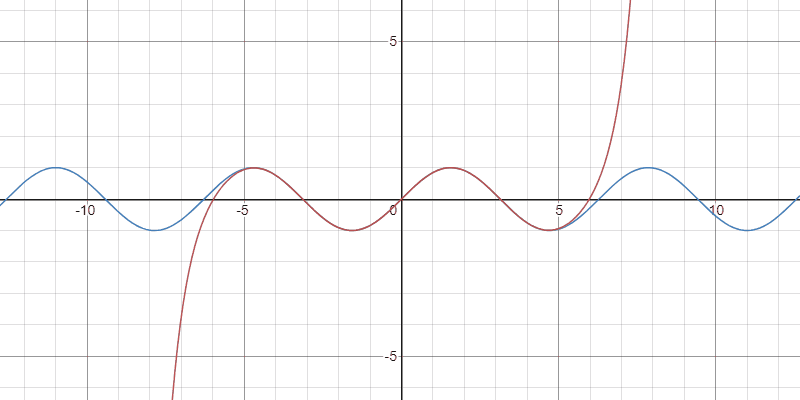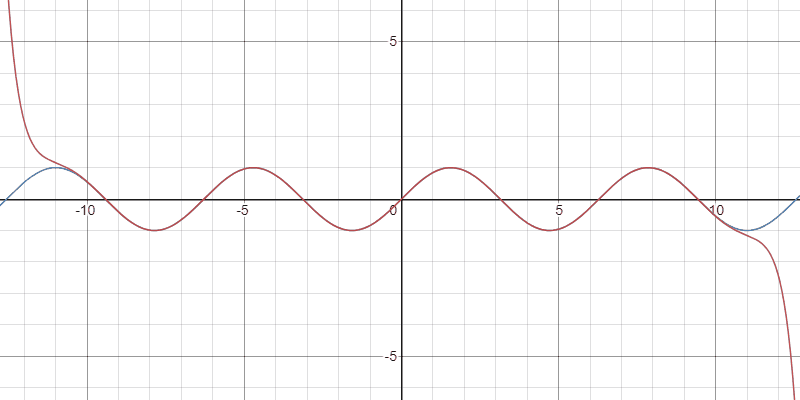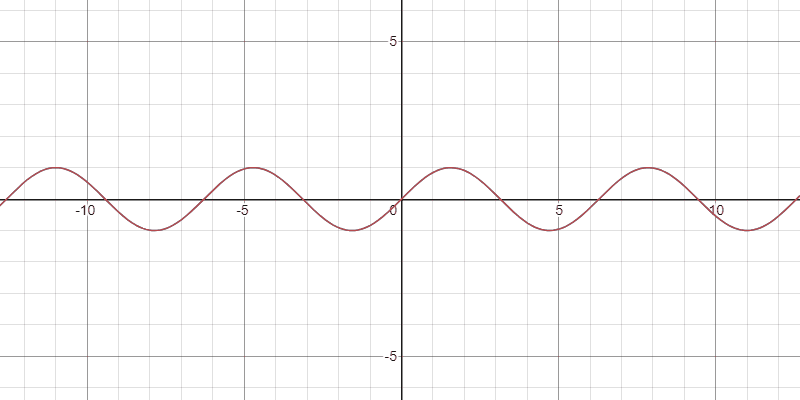Taylor多項式の収束の様子
$x>0$のとき，任意の正の整数$\ell$に対して次式が成り立つ：
$$ \sum_{n=0}^{2\ell-1}\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}\le\sin(x)\le\sum_{n=0}^{2\ell-2}\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}.$$
（もちろん，$x<0$のときは逆向きの不等式が成り立つ．）
$L:=\pi/x$とおき，関数$g(t):=\max\{(1-t)^{2k-1},0\}$に対して$\cos$のときにも使った補題を使うと，Taylor展開の剰余項について
\begin{align*}
\int_{0}^{1}(1-t)^{2k-1}\sin(tx)\,dt
&=\sum_{m=1}^{\infty}\int_{(2m-2)L}^{2mL}g(t)\sin(tx)\,dt
\ge 0
\end{align*}
となるから，あとは$(-1)^k$の符号を見ればよい．
任意の$x\in\mathbb{R}$に対して，次式が成り立つ：
\begin{align*}
\sin(x)&=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}.
\end{align*}
$$ \bigg|\frac{(-1)^{k}x^{2k}}{(2k-1)!}\int_{0}^{1}(1-t)^{2k-1}\sin(tx)\,dt\bigg|\le \frac{|x|^{2k}}{(2k-1)!}\to 0 \qquad (k\to\infty)$$
となる．
$\sin(1)$は無理数である．
もし$\sin(1)$が有理数であれば，互いに素な正の整数$k,\ell$を用いて$\sin(1)=\ell/k$と表せる．このとき$\sin(x)$のTaylor展開に$x=1$を代入した
\begin{align*}
\sin(1)=\sum_{n=0}^{k}\frac{(-1)^{n}}{(2n+1)!}+\frac{(-1)^{k+1}}{(2k+1)!}\int_{0}^{1}(1-t)^{2k+1}\sin(t)\,dt
\end{align*}
より
\begin{align*}
\int_{0}^{1}(1-t)^{2k+1}\sin(t)\,dt&=(-1)^{k+1}\bigg(\frac{(2k+1)!\ell}{k}-\sum_{n=0}^{k}\frac{(2k+1)!(-1)^n}{(2n+1)!}\bigg)
\end{align*}
が成り立つ．この右辺が整数であるのに対して，左辺については
\begin{align*}
0<\int_{0}^{1}(1-t)^{2k+1}\sin(t)\,dt<1
\end{align*}
となり整数でないから矛盾．
例４：対数関数
$2$以上の任意の整数$k$と$x\in(-1,\infty)$に対して
$$ \color{red} \log(1+x)=\sum_{n=1}^{k-1}\frac{(-1)^{n-1}}{n}x^{n}+(-1)^{k-1}x^{k}\int_{0}^{1}(1-t)^{k-1}(tx+1)^{-k}\,dt$$
が成り立つ．
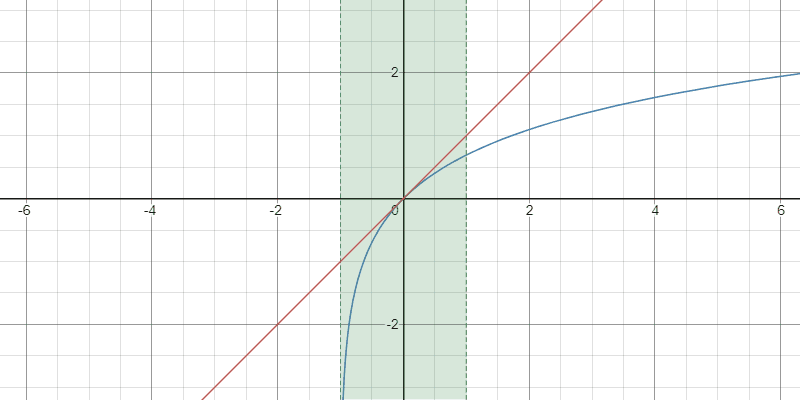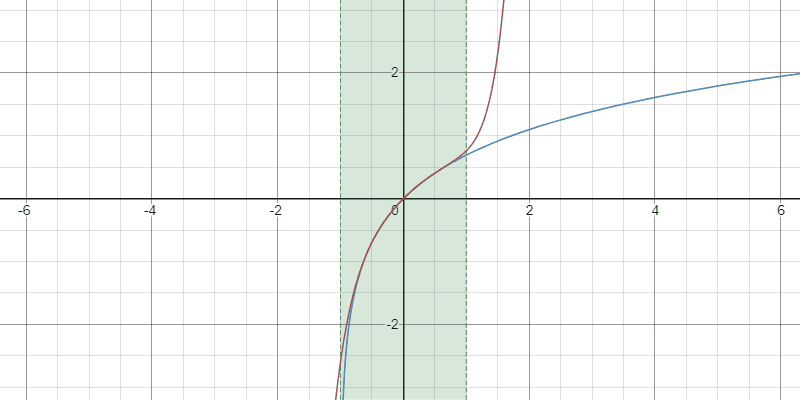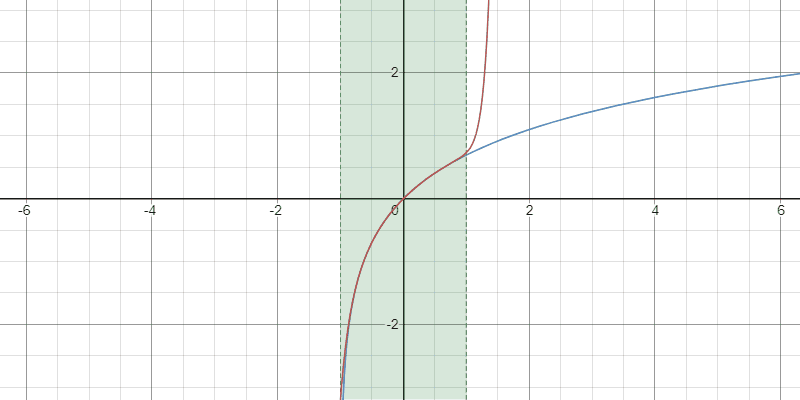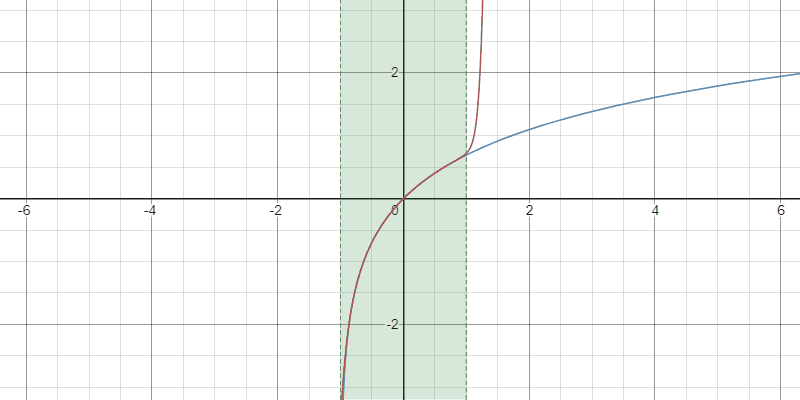Taylor多項式の収束の様子
$$\log(2)=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}.$$
十分小さい任意の$\varepsilon>0$に対して，Taylor展開の剰余項を
\begin{align*}
\bigg|(-1)^{k-1}\int_0^1 (1-t)^{k-1}(t+1)^{-k}\,dt\bigg|
&\le \int_{0}^{\varepsilon}1\,dt+\int_{\varepsilon}^{1}(1-\varepsilon)^{k-1}(\varepsilon+1)^{-k}\,dt \\
&=\varepsilon+\bigg(\frac{1-\varepsilon}{1+\varepsilon}\bigg)^k
\end{align*}
と評価すれば
\begin{align*}
\limsup_{k\to\infty}\bigg|(-1)^{k-1}\int_0^1 (1-t)^{k-1}(t+1)^{-k}\,dt\bigg|\le\varepsilon
\end{align*}
となり，$\varepsilon$の任意性より剰余項は$k\to\infty$のとき$0$に収束する．
Taylor展開 (多変数)
表記が簡単なので，多重指数の記法を使う．
$\Omega$を$\mathbb{R}^d$の開集合とする．
- $\mathbb{N}^d$の元を多重指数という．
- 多重指数$\alpha\in\mathbb{N}^d$と$x\in\mathbb{R}^d$に対して，次のように書く．
\begin{align*} \alpha!&:=\alpha_1!\cdots\alpha_d!, \\ |\alpha|&:=\alpha_1+\cdots+\alpha_d,\\ x^\alpha&:=x_1^{\alpha_1}\cdots x_d^{\alpha_d}. \end{align*} - 多重指数$\alpha\in\mathbb{N}^d$と$C^{|\alpha|}$級関数$f:\Omega\to\mathbb{R}$に対して，
$$ D^\alpha f:=\partial_1^{\alpha_1}\cdots\partial_d^{\alpha_d}f$$
と書く（$f$の$|\alpha|$階までの偏導関数は偏微分の順番に依らないことに注意）．
$k$を正の整数，$\Omega$を$\mathbb{R}^d$の開集合，$f:\Omega\to\mathbb{R}$を$C^{k}$級関数とする．
このとき，任意の$a,x\in\Omega$に対して，$a,x$を結ぶ線分が$\Omega$に含まれていれば
$$ f(x)=\sum_{|\alpha|< k}\frac{D^{\alpha}f(a)}{\alpha!}(x-a)^{\alpha}+k\sum_{|\alpha|=k}\frac{(x-a)^{\alpha}}{\alpha!}\int_{0}^{1}(1-t)^{k-1}D^{\alpha}f(tx+(1-t)a)\,dt$$
が成り立つ．
1変数関数$g:[0,1]\to\mathbb{R}$を
$$ g(t):=f(tx+(1-t)a) \qquad (t\in[0,1])$$
で定めると，$g$は$C^k$級だから1変数関数のTaylor展開より
$$ g(1)=\sum_{n=0}^{k-1}\frac{g^{(n)}(0)}{n!}+\frac{1}{(k-1)!}\int_{0}^{1}(1-t)^{k-1}g^{(k)}(t)\,dt$$
が成り立つ．この式に$g(1)=f(x)$と
$$ g^{(n)}(t)=\sum_{|\alpha|=n}\frac{n!}{\alpha!}(x-a)^{\alpha}D^{\alpha}f(tx+(1-t)a) \qquad (n=0,1,\ldots,k)$$
を代入すれば所望の等式を得る．
$$ f(x)=f(a)+\langle\nabla f(a),x-a\rangle+\int_0^1(1-t)\langle \nabla^2f(tx+(1-t)a)(x-a),x-a\rangle\,dt.$$
ここで，$\nabla^2f(\xi):=(\partial_{i}\partial_{j}f(\xi))_{d\times d}$は$f$のHessian matrixとした．
この記事を高評価した人
この記事に送られたバッジ
投稿者
