競技積分を始めよう　(駒場理数アドカレ 11/17)

私は 駒場理数サークル というものに所属しており、そこでアドカレが企画されました。これはその11/17分の記事です。

はじめに

高校数学の数学Ⅲ（数Ⅲ）での一つの大きなジャンルである、積分。数Ⅲの積分においても、King's Propertyやワイエルシュトラス置換など様々なテクニックを用いて問題を解くことがありますが、数3の積分は物足りない!　と感じたことがあるのではないでしょうか。今回の記事で取り扱う積分は、そんな高校数学を超えた積分であり、そこでは多彩なテクニック、公式、そして発想を用いて一見複雑怪奇な積分の閉じた形式を求める必要が生じます。
そこが個人的には積分の重要な魅力だと思うのですが、私の所感はおいて、そのような積分を解けるようになるにはどうすれば良いのか、つまり高校範囲を超えた積分(以降競技積分と呼称)に馴染みのない方向けの指南がこの記事の目的です。
私自身まだまだ学習中であり、そのような人間がこういう類の文章を書くのは少し気が引けますが、積分erをもっと増やしたい、積分の楽しさを知ってほしいという一心でなるべく丁寧に書いていこうと思っています。

目次

やや記事が長くなるので、目次から読みたい章を選んで読まれるのが良いと思います。

問題を見たときに考えること

この章では、積分を解く際に頻繁に用いるテクニックを紹介します。次の章では、実際に私が直近解いた問題を例示して、その時私がどのような思考をしながら積分を解いていったのかを視覚化します。それを通じて、問題を見たときに考えることを体系化することを目的とします（※これは、かなり受験数学的、あるいは競技数学的な考え方だと思います。積分は必ずしも定まった解法があるとは限らず、実際私が普段扱うものはそういったたぐいのものではあるのですが、問題を解くという点に今回は特化します）。
用いる公式、定理は後で一覧として記載するので、見知らぬ式や定理を使っていても、その式自身よりかは、どのような自体に遭遇してその公式を使うという選択を採ったのか、という点に注目すると良いと思います。とはいえ、最低限必要な公式は先に挙げておきます。また、よく用いる特殊関数も先に挙げておきます。なお、先に述べたような数Ⅲでの積分公式は既知のものとします。

積分を解く際によく用いる公式

\begin{align} &\sum_{n=0}^{\infty}x^n=\frac{1}{1-x} \quad (|X|<1) \\ &\sum_{n=0}^{\infty}\binom{a}{n}x^n=(1-x)^a,\binom{a}{n}=\frac{a(a+1)(a+2)\cdots(a+n-1)}{n!}\\ &e^{i\theta}=\cos\theta+i\sin\theta \\ &\ln(z)=\ln(|z|)+i\arg(z) \end{align}

特殊関数

まだまだ必要な公式はありますが、いったんこれくらいに留めておきます。最初はこれほど覚えないといけないのか、と圧倒されるかもしれませんが、積分をいくつも解いているうちにだんだんと染みついてきますし、また使うたびに調べても問題ありません(私も三角関数の部分分数展開などはあやふやで、毎回Wikipediaで調べています)。
次の章で、実際に問題を挙げて、どのように積分を解いていくかを解説したいと思います。

テクニック1 級数に直す

最初は$\ln x=t$と置換してみたり、$1/(1-x)$で部分積分したりと数３で習った手法を試してみましょう。やってみると分かりますが、そこからの手が思い浮かびません。そこで打開策として、先ほどのよく使う公式で挙げた幾何級数の和の公式
$$\frac{1}{1-X}=\sum_{n=0}^{\infty}X^n\quad(|X|<1)$$
を用いてみます。ここで、当の積分は$x=1$を積分区間に含んでおり、上の公式は$|x|<1$を必要とすることから適用できないのではないか、と考える人がいると思います。それは尤もな疑問ですが、いったん措いておきます。また、ひとまず無限和と積分の交換も認めます。
\begin{align} \int_{0}^{1}\frac{\ln x}{1-x}\d x=\int_{0}^{1}\ln x\cdot\qty(\frac{1}{1-x})\d x&=\int_{0}^{1}\ln x\sum_{n=0}^{\infty}x^n\d x \\ &=\sum_{n=0}^{\infty}\int_{0}^{1}x^n\ln x\d x \end{align}
これで、積分を無限級数として表すことが出来ました。複雑なままでは、と思うかもしれませんが、無限級数の項である積分をよく見てみると、これは$\ln x$で部分積分をすると、解けることが分かります。どういうことかというと、
\begin{align} \int_{0}^{1}x^n\ln x\d x&=\int_{0}^{1}\qty(\frac{x^{n+1}}{n+1})'\ln x\d x \\ &=\lim_{\varepsilon\to0+}\qty[{\frac{x^{n+1}}{n+1}}\ln x]^{1}_{\varepsilon}-\frac{1}{n+1}\int_{0}^{1}x^{n+1}\qty(\ln x)'\d x \\ &=0-\frac{1}{n+1}\int_{0}^{1}x^n\d x =-\frac{1}{(n+1)^2}\qty[{x^{n+1}}]_{0}^{1}=-\frac{1}{(n+1)^2} \end{align}
これをもとの式に代入しましょう。すると、
\begin{align} \int_{0}^{1}\frac{\ln x}{1-x}\d x=\sum_{n=0}^{\infty}\frac{-1}{(n+1)^2}=-\sum_{n=1}^{\infty}\frac1{n^2}=-\frac{\pi^2}{6} \end{align}
最後の等号は、リーマンゼータ関数の特殊値を用いました。
これで、無事に問題１の解が得られましたね。このように、いくつかの積分は、被積分関数の一部をTaylor展開し、無限級数として表したのちに、級数の項であるそれぞれの積分を求めて、最後に得られた級数を計算するという手法が有効です。注意点としては、必ずしも得られた級数が既知のものであるとは限らないこと、及び、どの部分を展開するかを選ぶには経験を必要とすること、です。次の例を考えてみます。

展開するべきものとしては、$\frac1{1+x^2}=\sum_{n=0}^{\infty}(-1)^nx^{2n}$または$\ln(1+x)=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}x^n}{n}$が考えられますが、実はそのどちらもあまりいい手段ではありません。というのも、級数に展開したあとの各項の積分が、なかなか綺麗に求められないためです(試してみてください)。このように、級数に直す方法が使えないことも数多くあります。
私の場合は、積分を見てまず最初に試すテクニックであり、解ける場合もたまにあるが難しい積分だとほとんど通用しない、という印象です。とはいえ、かなり使いやすいテクニックで、初心者でも簡単にいろいろな積分の問題を解くことが出来ます。高校範囲を超えた積分が解ける感動も大きいと思うので、以下に示す例題をぜひ解いてみてください。

テクニック2 ファインマントリック

問題１の被積分関数の逆数が被積分関数となっている問題です。これは、どの部分も級数展開できそうにないですね($\ln x$の逆数の級数展開もあるにはありますが、非常に複雑で実用性に乏しいです)。この問題は、実はファインマントリックと呼ばれるテクニックが使えます。YouTubeでFeynmann's trickなどと検索すれば動画が山ほど出てくるので、これも初心者の問題としては非常に潤沢な題材です。ファインマントリックとは、厳密性を無視してざっくり言うと、以下のようなものです。

主張としては、インテグラルと微分を交換できる、というものです。これをどのように積分を用いるかというと、与えられた積分の被積分関数にうまいこと新たな変数を導入し、その積分全体を導入した変数を引数とする関数とみなします。そしてその変数で微分することで積分を簡単な(閉じた形を求められる)ものとし、積分を解いたのちに両辺を導入した変数で積分して元の形を復元する、という方法です。
言葉よりも実際の使い方を見たほうが分かりやすいので、問題2を解きつつ説明します。
突然ですが、以下のように見ます。
$$\int_{0}^{1}\frac{x-1}{\ln x}\d x=\left.{\int_{0}^{1}\frac{x^{\alpha}-1}{\ln x}\d x}\right|_{\alpha=1}$$
(右の縦線は$\alpha=1$を代入するという意味)
後にも述べますが、ファインマントリックを使う上で一番の難所がこの、どのように変数を導入するか？という点です。何も知らない状態からこれを思いつくのは至難の業、あるいは不可能ですし、知らないとできるはずがない導入の仕方をすることもあります。なので、いったんどうしてこのように置くのか、という点には目をつむっていただきたいです。
$$I(\alpha)=\int_{0}^{1}\frac{x^{\alpha}-1}{\ln x}\d x$$
とすると、求める積分は$I(1)$です。両辺を$\alpha$で微分すると、
\begin{align} I'(\alpha)=\int_{0}^{1}\dv{}{\alpha}\frac{x^{\alpha}-1}{\ln x}\d x &=\int_{0}^{1}\frac{x^{\alpha}\cdot \ln x}{\ln x}\d x \\ &=\int_{0}^{1}x^{\alpha}\d x=\frac{1}{\alpha+1} \end{align}
よって、
$$I'(\alpha)=\frac1{\alpha+1}$$
両辺を積分することで、
$$I(\alpha)=\ln(\alpha+1)+C\quad(C=const.)$$
となります。最後にこの積分定数$C$を決めましょう。もとの$I(\alpha)$の定義式において$\alpha=0$を代入してみます。すると、
\begin{align} I(0)&=\ln(1+0)+C=C \\ &=\int_{0}^{1}\frac{x^0-1}{\ln x}\d x=\int_{0}^{1}\frac{0}{\ln x}\d x=0 \\ \therefore C=0 \end{align}
よって$I(\alpha)=\ln(\alpha+1)$であることが分かり、ここに$\alpha=1$を代入することで、
$$\int_{0}^{1}\frac{x-1}{\ln x}\d x=I(1)=\ln 2$$
が求まりました。
新たな変数を導入して積分自体を関数とみなし、元の積分をその関数の特殊値とみなすという考えは、私自身初めて知った時衝撃的でした。被積分関数が到底積分できそうにない時でも、上手く変数を導入してから微分すると実は綺麗な形になってしまう、という点も非常に面白いです。先に言った通り、ファインマントリックを扱った動画はYouTube上に数多あるので、それらを視聴するのがこのテクニックの習得に役立つと思います。
注意点としては、強調したように変数導入についてです。適当に追加したのではうまくいかないことが多く、経験が何よりであると言えます。例えば、問題2はなぜあのように導入したのかというと、$x^{\alpha}$という項を$\alpha$で微分することで分母の$\ln x$を消せるからですが、これはなかなか初見では思いつけません。また、上手く変数を導入し、微分後の積分が求められたとしても、その$I'(\alpha)$の積分自身が解けない、なんてことも起きたりします。がしかし、よくある変数導入としては、
\begin{align} &\frac{x-1}{\ln x}\to \frac{x^{\alpha}-1}{\ln x}\\ &\frac{\ln(x)}{x}\to\frac{\ln(\alpha+x)}x \\ &\frac{1}{x}\to\frac{e^{\alpha x}-1}{x} \\ &\frac{\sin x}{x}\to \frac{\sin(\alpha x)}{x} \end{align}
などでしょうか。いずれも、$\alpha$で微分すると良い形になることが分かると思います。最後に例題を載せます。どのように変数を導入するか、試行錯誤しながら考えてみてください。

テクニック 3 パラメータでの微分

テクニック4で積分にパラメータを導入しました。このパラメータの利用方法として、一回微分して積分を簡単にする以外にも、微分をする前の関数を求めてしまい、そこから微分をして微分係数を見ることで$\ln x$などが入った積分の計算に利用できる場合があります。例えば、例題の積分について、少し変形をすることで、
\begin{align} \int_{0}^{1}\frac{\ln x}{\sqrt{1-x^3}}\d x &= \frac19\int_{0}^{1}\frac{\ln y}{y^{\frac23}\sqrt{1-y}}\d y \quad (y=x^3) \\ &=\frac19\int_{0}^{1}y^{-\frac23}(1-y)^{-\frac12}\ln y\d y \end{align}
となることから、直ちにこの積分がベータ関数の微分形であることが、すなわち
\begin{align} \int_{0}^{1}\frac{\ln x }{\sqrt{1-x^3}}\d x = \frac19\left.\dfrac{\partial }{\partial s}{\int_{0}^{1}y^s(1-y)^{-\frac12}} \d y\right|_{s=-\frac23} \end{align}
と表せることが分かると思います。ベータ関数はガンマ関数との関係式を持ち、ガンマ関数の微分(厳密には対数微分)はディガンマ関数で表せることから、元の問題の解はディガンマ関数の特殊値で表せそうなことが分かりますね。そこまで予想したところで、実際に計算してみます。
\begin{align} \left.\dfrac{\partial }{\partial s}{\int_{0}^{1}y^s(1-y)^{-\frac12}} \d y\right|_{s=-\frac23}&=\left.\dfrac{\partial }{\partial s}B\qty(s+1,\frac12)\right|_{s=-\frac23} \\ &=\left.{\frac{\Gamma(s+1)\Gamma(\frac12)}{\Gamma(s+\frac32)}}\right|_{s=-\frac23}\\ &=\left. \frac{\Gamma(s+1)\Gamma(\frac12)\left[\psi(s+1)-\psi(s+\frac32)\right]}{\Gamma(s+\frac32)}\right|_{s=-\frac23} \\ &=\frac{\Gamma(\frac13)\Gamma(\frac12)(\psi(\frac13)-\psi(\frac56))}{\Gamma(\frac56)} \end{align}
ディガンマ関数の差の積分表示
$$\psi(x)-\psi(y)=\int_{0}^{1}\frac{t^{y-1}-t^{x-1}}{1-t}\d t$$を用いて計算をすると、
\begin{align} \psi\qty(\frac13)-\psi\qty(\frac56)=2\ln 2-\frac{2\sqrt 3}{3}\pi \end{align}
となります(計算練習)。また、ガンマ関数の方にも相反公式や倍角公式を用いて整理することで、
\begin{align} \int_{0}^{1}\frac{\ln x}{\sqrt{1-x^3}}\d x =\frac{\Gamma^3(\frac13)}{3\sqrt[3]{2}\sqrt3 \pi }\qty(\ln2 - \frac{\pi}{\sqrt{3}}) \end{align}
と閉じた形が得られます。
先にも少し言及しましたが、$\ln x$のべき乗が被積分関数にある場合はこのテクニックで解ける場合が多くあります。また、初等関数の積分で、このテクニックを用いずとも計算で気はするものの、パラメータでの微分を繰り返すことで計算が簡単になるような積分も偶に出会うことがある気がします。
注意点などはテクニック3と同じなので割愛

テクニック 4 複素数の導入

一部の問題は、被積分関数を複素関数の実部または虚部であるものとしてみると見通しが良くなることがあります。上の積分を解きます。先ほどの級数展開のテクニックを踏まえると、積分区間で$|\cos^4 x|\le 1$であることから級数展開を用いることを考えるかもしれません。いったんそれを試してみましょう。
\begin{align} \int_{0}^{\frac\pi 2}\ln(1+\cos^4x)\d x=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\int_{0}^{\frac\pi2}\cos^{4n}x\d x \end{align}
さて、数３の受験数学で典型とも言えるウォリス積分というものがあります。

($\beta_n$という略記はかなりマイナーなようですが、これを用いるとスッキリするので使います。)
よって、$n\to2n$として、
$$\int_{0}^{\frac\pi2}\ln(1+\cos^4 x)\d x=\frac\pi2\sum_{n=1}^{\infty}\frac{(-1)^{n-1}\beta_{2n}}{n}$$
……級数にはできましたが、ここから詰まってしまいます。頑張ってこの級数を解くことも非常に興味深い問題なのですが、今回は複素関数を導入することで楽に解きましょう。
「積分を解く際によく用いる公式」の小見出しで挙げた通り、$\Re \ln(a+ib)=\frac12\ln(a^2+b^2)\quad a,b\in\mathbb{R}$です。これを利用して、
\begin{align} \int_{0}^{\frac\pi2}\ln(1+\cos^4 x)\d x&=2\Re\int_{0}^{\frac\pi2}\ln(1+i\cos^2x)\d x \\ &=2\Re\sum_{n=1}^{\infty}\frac{(-1)^{n-1}i^n}{n}\int_{0}^{\frac\pi2}\qty(\cos x)^{2n}\d x \\ &=-\pi\Re\sum_{n=1}^{\infty}\frac{(-i)^n}{n}\beta_n \end{align}
となります(テクニック１も用いました)。さっきの級数と大して違いがないように見えますが、$\beta$の添え字が$2n$から$n$になっています。実はこの差がかなり重要なのですが、ひとまずこの級数を求めることとしましょう。
$$f(x)=\sum_{n=1}^{\infty}\frac{\beta_n}{n}x^n$$とします。求める級数は$-\pi \Re f(-i)$です。分母の$n$が邪魔なので、両辺を$x $で微分すると、
$$f'(x)=\sum_{n=1}^{\infty}\beta_nx^{n-1}$$
となります。
実は、$\binom{-\frac12}{n}=(-1)^n\beta_n$が成り立ちます(計算練習)。これと「積分を解く際によく用いる公式」で挙げた一般化二項定理を用いると、
\begin{align} \sum_{n=0}^{\infty}\beta_nx^{2n}=\sum_{n=0}^{\infty}\binom{-\frac12}{n}(-x^2)^{n}=(1+x^2)^{-\frac12}=\frac{1}{\sqrt{1-x^2}} \end{align}
となります。大分$f'(x)$の級数表示に近づいてきましたが、やや異なっているので調整をすると、
$$f'(x)=\frac{\frac{1}{\sqrt{1-x}}-1}{x}$$
と表せることが分かります(計算練習)。よって、
\begin{align} f(x)=\int_{0}^{x}f'(t)\d t=\int_{0}^{x}\frac{\frac1{\sqrt{1-t}}-1}{t}\d t=2\ln\qty(\frac{2}{1+\sqrt{1-x}}) \end{align}
となります(この積分自体は数３の知識で解けるので割愛)。
以上より、問題３の解は、
\begin{align} \int_{0}^{\frac\pi2}\ln(1+\cos^4x)\d x=-\pi \Re f(-i)&=-2\pi \Re \ln\qty(\frac2{1+\sqrt{1+i}}) \\ & =-2\pi\Re\qty({\ln 2-\ln(1+2^{\frac14}e^{\frac{\pi i}{8}})}) \\ &=\pi\ln\qty(\frac{1+\sqrt2+\sqrt2\sqrt{1+\sqrt2}}{4}) \end{align}
と閉じた解が得られました。
問題が良くなく、複素関数として見ることの恩恵が少し分かりにくいのかもしれませんが、刺さるときは著しく刺さります。注意点としては、複素関数は多価性があることが多いので、どの枝を選ぶかを十分に吟味する必要があることくらいでしょうか。あとは、ファインマントリックと同様ですが、どのような時に有効かが少し慣れないと見えてこないことです。最後に例題を挙げます。

テクニック 5 留数定理

気持ちいいアレです。留数定理、あるいはコーシーの積分定理を正しく用いようとすると複素関数論の知識をある程度学ばないといけないのですが、積分を解くだけだったらほとんど気にしなくて大丈夫じゃないかなと思います。複素積分は詳しくは説明しません。
さて、この積分を特にあたって、まずは級数展開を考えましょう。
\begin{align} \int_{-\infty}^{\infty}\frac{\cosh(s x)}{\cosh(\pi x)}\d x&=4\sum_{n=0}^{\infty}(-1)^n\int_{0}^{\infty}e^{-(2n+1)\pi x}\cosh(sx)\d x \\ &=4\sum_{n=0}^{\infty}\frac{(-1)^n(2n+1)\pi}{(2n+1)^2\pi^2-s^2} \end{align}
一応ここからもディガンマ関数の級数表示や相反公式を用いることで計算できるのですが、やや面倒です。そこで、複素積分を用いてこの積分を計算することを考えてみましょう。
$f(z)=\frac{\cosh(s z)}{\cosh(\pi z)}$とし、積分経路を
$$-R,R,R+i,-R+i\text{の４点を頂点とする長方形の辺}$$
Desmosで作成
とします。この長方形の領域内部の正則でない点は$z=\frac i2$で、そこで1位の単純極となります。
よって、$$\int_{\sum_{i}\Gamma_i}f(z)\d z=2\pi i\Res_{z=\frac i 2}f(z)=2\pi i\lim_{z\to\frac i2}\frac{\cosh(s z)(z-\frac i2)}{\cosh(\pi z)}=2\cos(\frac s2)$$
\begin{align} &\int_{\Gamma_1}f(z)\d z=\int_{-R}^{R}\frac{\cosh(sz)}{\cosh(\pi z)}\d z \\ &\int_{\Gamma_3}f(z)\d z=\int_{R}^{-R}\frac{\cosh(s(z+i))}{\cosh(\pi(z+i))}\d z=\int_{-R}^{R}\frac{\cosh(sz)\cosh(si)+\sinh(sz)\sinh(si)}{\cosh(\pi z)}\d z=\cos(s)\int_{-R}^{R}\frac{\cosh(sz)}{\cosh(\pi z)} \\ &\int_{\Gamma_2}f(z)\d z,\int_{\Gamma_4}f(z)\d z\longrightarrow0\quad(R\to \infty) \end{align}
であるので、$R\to\infty$のとき、
\begin{align} \int_{-\infty}^{\infty}\frac{\cosh(sz)}{\cosh(\pi z)}\d z=\frac{2\cos(\frac s2)}{1+\cos(s)}=\frac{1}{\cos(\frac s2)} \end{align}
と求まりました。(気持ちいい！)
また、初めのアプローチで級数展開を行っていたので、ここから逆に
$$\frac{1}{\cos x}=2\sum_{n=0}^{\infty}\frac{\left(n+\frac{1}{2}\right)\left(-1\right)^{n}\pi}{\left(n+\frac{1}{2}\right)^{2}\pi^{2}-x^{2}}$$という副産物も得られます(三角関数の部分分数展開)。

留数定理は積分を解く上で非常に強力なツールなのですが、ここまでのテクニックを見てきて分かる通り、万能というわけではありません。積分経路を選ぶ上での工夫が求められます。
例えば、今回の場合、$\cosh$の周期性から、$\Gamma_1,\Gamma_3$の積分が定数倍の関係になり、また$\Gamma_2,\Gamma_4$の積分が$R\to\infty$の極限で0に収束することから、留数を見るだけで良くなりました。複素積分で頻繁に見る経路では、例えば上半平面での半円経路などがありますが、今回の場合難があります(そもそも、被積分関数$f(z)$は$|f(x+iy)|$の$y\to\infty$で有界ではありませんし、$(\mathbb{Z}+\frac12)i$に極を持つため留数の和が級数のようになります)。コーシーの積分定理によれば、正則な領域内を動くのであれば積分経路は自在に取れるのですが、人間が手で計算するうえで扱いやすい経路を見つけることが求められます。
Pochhammer積分路の図 / ベータ関数のポッホハマー積分路を用いた積分表示（ガンマ関数論・複素積分）( https://mamekebi-science.com/math/spetialfunction/beta-pochhammer/ )より引用
また、積分計算を留数計算に落とし込むにあたり、一部の経路での積分値が0に収束する必要があるので、求めたい積分の積分区間が有限だと使えない場合が多いように思われます。
どのテクニックも同じ結論に終始していますが、経験が大事になります。
とはいえ複素積分はこういった積分求値のテクニックに限らずとも大変有用な手法であり、例えばアーベルプラナの和公式などは複素積分の強力さを示す例です。
あえて経路選択のアイデアを述べるとすれば、
①被積分関数に虚数方向の(擬)周期性がある場合は長方形経路
②積分区間が$[0,2\pi],[0,\pi]$の場合は$z=e^{i\theta}$として円周経路
③被積分関数の分母が$\pi^2+\varphi(x)^2$の形になっている場合は$(\varphi(x)+\pi i)(\varphi(x)-\pi i)$と分解して長方形経路
くらいかな、と思います。
経路選択の他にも注意点はあり、例えば$\ln z$など分岐点を含むような関数を積分する場合は分枝切断をする必要があるのですが、それはこの記事でつたない解説をするよりは、しっかりとした複素解析の本が数多あるのでそちらを参考にしてください。これ以上込み入った話をすると記事を書いた人間の知識の浅さが露呈しそうなので止めておきます。

テクニック6 特殊関数

体感ですが、普段解く積分の７割くらいは特殊関数の特殊値に帰着すると思っています。また、専門的な知識を要する積分も大体が特殊関数の理論が要となっているのではないでしょうか。
・ガンマ関数
・ポリガンマ関数
・リーマンゼータ関数
・ディリクレベータ関数
・多重対数関数(ポリログ)
・フルウィッツのゼータ関数
・クラウゼン関数
・楕円積分
・ベッセル関数
・超幾何関数
これらの特殊値や関係式などを都度用いて解いていきます。また、級数表示のあるような特殊関数の場合は、テクニック1(積分を級数にする)との合わせ技もかなりの頻度で行われます。このテクニックはこれまでのものとは趣向が異なり、知識勝負です。
では問題を解いていきましょう。
これはあまり特殊関数とは関係ないのですが、ポアソン核(Poission Kernel)というものがあり、
$$\sum_{n=0}^{\infty}r^ne^{ni\theta}=\frac{1-re^{-i\theta}}{1+r^2-2r\cos\theta}\quad(|r|<1)$$
が成り立ちます。よく見ると、今回の分母は$r=-\frac12$とした場合のポアソン核になっていることが分かります。そのため、
\begin{align} \int_{0}^{\pi}\frac{\theta^2}{5+4\cos \theta}\d \theta&=\int_{0}^{\pi}\theta^{2}\left(\frac{2}{3}\sum_{n=0}^{\infty}\left(-\frac{1}{2}\right)^{n}\cos\left(n\theta\right)-\frac{1}{3}\right)\d\theta \\ &=\frac{2}{3}\sum_{n=1}^{\infty}\left(-\frac{1}{2}\right)^{n}\int_{0}^{\pi}\theta^{2}\cos\left(n\theta\right)\d\theta-\frac{\pi^{3}}{9}\\ &=-\frac{4\pi}{3}\sum_{n=1}^{\infty}\frac{1}{2^nn^{2}}-\frac{\pi^{3}}{9} \end{align}
となります。ただし$\theta^2\cos(n\theta)$の積分は部分積分を行っています。
ここで最後の級数として$\displaystyle \sum_{n=1}^{\infty}\frac{1}{2^nn^2}$というものが出てきました。これは多重対数関数
\begin{align} \operatorname{Li}_s(z)=\sum_{n=1}^{\infty}\frac{z^n}{n^s} \end{align}
の$s=2,z=\frac12$とした場合の値であり、実は$\operatorname{Li}_{2}(z)$には、$\operatorname{Li}_2(z)+\operatorname{Li}_2(1-z)=\frac{\pi^2}{6}-\ln (z)\ln (1-z)$という相反公式があるので、ここに$z=\frac12$を代入することで、
\begin{align} &2\operatorname{Li}_2\qty(\frac12)=\frac{\pi^2}{6}-\ln^2(2) \\ &\therefore \operatorname{Li}_2\qty(\frac12)=\frac{\pi^2}{12}-\frac{\ln^2 2}{2} \end{align}
となります。よって、元の積分の解は
\begin{align} \int_{0}^{\pi}\frac{\theta^2}{5+4\cos\theta}\d \theta=\frac{2\pi}{3}\ln^{2}2-\frac{2\pi^{3}}{9} \end{align}
と分かりました。この解説を見て、「なんだかよくわからないうちに色々な言葉が出てきて混乱した」という感想を抱いたかもしれませんが、特殊関数を用いる積分は大体こういう調子で、ナゾの関数が○○として定義されて、その関数は△△という関係式を満たし、また特殊値は××な形が多い気がします。それぞれの特殊関数は当然深い理論や洞察すべき特性を持っているのでしょうが、積分を解くために特殊値を「借りる」だけであれば、ただ覚えるだけの話です。
ところで、今回の問題は$\operatorname{Li}_2\qty(\frac12)$が閉じた表現を持っていたので良かったのですが、積分を解いていると、ある特殊関数に特定の引数を代入した値(例えば$\ln(\Gamma(\frac13))$など)が積分の解になることもしばしばあります。元の特殊関数は級数か、あるいは積分などで定義されているわけで、言ってしまえば積分を別の積分で表しただけともみなせてしまう。そのことに不満がある、あるいは、積分を解いたことにはならないのではないか、と感じる方もいるかもしれません。
私も以前はそう思っていたのですが、これは初等関数に限っても類似の事象は起きているわけです。例えば二次方程式$ax^2+bx+c=0,a\ne 0$は有理数解を持つこともありますし、無理数解、虚数解を持つこともあります。有理数と無理数とには大きな隔たりがありますが、これらの解は全て解の公式($a,b,c$を変数とする二価関数)を用いると統一的に表せます。つまり、ここで扱うような積分についても、それぞれの積分は特殊関数という「解の公式」のようなものを用いることで統一的に表現できる、ということが大切で、その「解の公式」から出てくる値が初等的か否かはそこまで気にする必要はないのでは、というのが私の結論です。同じ疑問を抱いている方の一助になればと私なりの考えを示しておきました。

テクニック7 その他

ここまでさまざまなテクニックを用いてきましたが、当然ながら積分の問題はなにか定まったテクニックを用いれば必ず解けるというようなものではなく、問題個別の解法やテクニックも存在します。例えば上の積分は Ahmed's integral と呼ばれる積分ですが、非常に技巧的な計算を要します(解法はリンク先を参照してください。ちなみに、難しい定積分などにはよく人名がついています)
またほかにも、 Glasser's master theorem や Lobachevsky integral formula などの積分公式が存在し、統一的な参照先はなかなかないのではないでしょうか。そういった公式を知る手段としては、YouTube,X,MSEなどで積分の問題に関する投稿を見るか、あるいはMathlogや個人ブログ(特に まめけびさんのサイト はおすすめです)でもある程度記事として情報がまとまっているのを参照することになるでしょう。このあたりの話題については、本記事の最後でも触れます。

実践

さて、おおまかなテクニックの紹介は終わったので、この章では私が最近解いた積分の問題を例に挙げて、どのように解いていったのかを思考過程も踏まえてなるべく正確に視覚化していきたいと思います。問題には、 KBHM さんが作成した 積分問題集2 から取り上げます。この問題集は、そこそこの難易度のものから高難易度のものまで多様な積分が集められており、またこの記事で紹介したテクニックを使える積分がたくさん含まれているので、ぜひ取り組んでみてください。

問題①

上下ともに$\arctan x$の項があり、積分区間も$[0,\infty)$であることからtan置換が使えそうです。しかし、上の積分は$\ln^2(1+x^2)$という項があり、tan置換をすると対数三角関数が出現し一筋縄ではいかなそうだったので、まずは下の積分に注力しました。
$\arctan \frac1x = \frac\pi 2-\arctan x\quad (0\le x)$という関係に注意すると、
\begin{align} I_2=2\int_{0}^{\frac\pi2}\frac{\qty(\frac\pi2-x)x^2}{\sin(2x)}\d x \end{align}
という形になります。
$$\int_{0}^{\frac\pi2}\frac{x^n}{\sin x}\d x$$という形の積分は、$\ln(\tan(\frac x2))$で部分積分を行ってからFourier展開をすることで一般に計算が可能なのですが、$I_2$の積分の分母にある$\sin 2x$は$x\to \frac\pi 2-x$という置換$^1$を行っても形が変わらないので、King Propertyを用いて、元の式と足し合わせる$^2$ことで少し分子を簡略化できるのではないか、と考えました。
\begin{align} I_2\overset{1}{=}2\int_{0}^{\frac\pi2}\frac{x(\frac\pi2-x)^2}{\sin(2(\frac\pi2-x))}\d x&=2\int_{0}^{\frac\pi2}\frac{x(\frac\pi2-x)^2}{\sin (2x)}\d x \\ &\overset{2}{=}\int_{0}^{\frac\pi 2}\frac{x(\frac\pi2-x)^2+(\frac\pi2-x)x^2}{\sin(2x)}\d x \\ &=\frac{\pi}{2}\int_{0}^{\frac\pi2}\frac{x(\frac\pi2-x)}{\sin(2x)}\d x \\ &=\frac{\pi}{8}\int_{0}^{\frac\pi2}\frac{x(\pi -x)}{\sin x}\d x \end{align}
予想通り分子の次数を減らすことが出来ました。ここからは部分積分$^3$をして、Fourier展開を考えれば$^4$難なく計算できそうです。
\begin{align} \frac\pi8\int_{0}^{\frac\pi2}\frac{x(\pi -x)}{\sin x}\d x&\overset{3}{=}-\frac\pi8\int_{0}^{\frac\pi2}(\pi -2x)\ln(\tan(\frac x2))\d x \\ &\overset{\text{※}_1}{=}-\frac\pi4\int_{0}^{\frac\pi2}(\pi - 2x)\ln(\tan x )\d x \\ &\overset{}{=}-\frac{\pi }{2}\int_{0}^{\frac\pi2}x\ln(\cot x)\d x \quad\qty(x\to \frac\pi2 -x) \\ &\overset{4}{=}-\pi\sum_{n=0}^{\infty}\frac{1}{2n+1}\int_{0}^{\frac \pi 2}x\cos(2(2n+1)x)\d x \\ &\overset{}{=}\frac\pi2\sum_{n=0}^{\infty}\frac{1}{(2n+1)^3} \quad\qty(\text{$\cos$で部分積分})\\ &\overset{}{=}\frac{7\pi }{16}\zeta(3)　\quad\qty({\sum_{n=0}^{\infty}\frac{1}{(2n+1)^3}=\sum_{n=1}^{\infty}\frac{1}{n^3}-\sum_{n=1}^{\infty}\frac{1}{(2n)^3}=\frac{7}{8}\zeta(3)}) \end{align}
ただし、$\text{※$_1$}$の変形は
\begin{align} \int_{0}^{\frac\pi2}(\pi -2x)\ln(\tan(\frac x2))\d x&=2\int_{0}^{\frac\pi4}(\pi-4 x)\ln(\tan x)\d x \\ &=2\int_{0}^{\frac\pi 4}(\pi -2x)\ln(\tan x)\d x-2\int_{0}^{\frac\pi 4}2x\ln(\tan x)\d x \\ &=2\int_{0}^{\frac\pi 4}(\pi -2x)\ln(\tan x)\d x-2\int_{\frac\pi 4}^{\frac\pi 2}2\qty(\frac\pi2-x)\ln(\tan (\frac\pi2-x))\d x \\ &=2\qty(\int_{0}^{\frac\pi4}+\int_{\frac\pi4}^{\frac\pi2})(\pi-2x )\ln(\tan x)\d x \\ &=2\int_{0}^{\frac\pi2}(\pi-2x )\ln(\tan x)\d x \end{align}
です。(この変形は最初から思いついたわけではなく、数値的に成り立ちそうだったために後から証明を与えました)
これで$I_2$の計算が行えました。次に$I_1$の計算に取り掛かりたいと思います。依然として$\ln^2(1+x^2)$という項が不穏で、$I_2$の方法を用いても計算できるかもしれませんが、分子の次数も下げられない以上非常に重い計算が待っているように思います。そこで、今度は$\tan$を置換するのではなく、級数展開に持ち込むことでどうにかなるのではないか、と思いました。
\begin{align} \arctan x=\sum_{n=0}^{\infty}\frac{1}{(2n+1\beta_n)}\frac{x^{2n+1}}{(1+x^2)^{n+1}}\quad\qty(x\in \mathbb{R},\beta_n=\frac{\binom{2n}{n}}{2^{2n}}) \end{align}
この$arctan$の級数展開は収束半径が∞で、今回の積分範囲の条件に合致します。また、項に出てくる$1+x^2$という部分と、元の積分の$\ln^2(1+x^2)$を見ると、テクニック4のパラメータでの微分ではないかと予想しました。実際に代入して計算してみると、
\begin{align} I_1&=\int_{0}^{\infty}\frac{\arctan \frac1x\ln^2(1+x^2)}{x}\d x \\ &=\sum_{n=0}^{\infty}\frac{1}{(2n+1)\beta_n}\int_{0}^{\infty}\frac{\ln^2(1+x^2)}{(1+x^2)^{n+1}}\d x \\ &=\sum_{n=0}^{\infty}\frac{1}{(2n+1)\beta_n}\left.{\dfrac{\partial^2}{\partial s^2}\int_{0}^{\infty}\frac{1}{(1+x^2)^s}}\d x\right|_{s=n+1} \\ &=\frac12\sum_{n=0}^{\infty}\frac{1}{(2n+1)\beta_n}\left.\dv{^2}{s^2}\frac{\Gamma(s-\frac12)\Gamma(\frac12)}{\Gamma(s)}\right|_{s=n;1} \\ &=\frac12\sum_{n=0}^{\infty}\frac{\Gamma(\frac12)\Gamma(n+\frac12)}{(2n+1)\beta_n\Gamma(n+1)}\left[{\left({\psi\qty(n+\frac12)-\psi(n+1)}\right)^2-\left(\psi_1\qty(n+\frac12)-\psi_1(n+1)\right)}\right] \end{align}
ここまできて、少し手が止まりました。というのも、ディガンマ関数やトリガンマ関数を引数に持つ、オイラー和に類似した級数となったからです。ガンマの方は、幸いなことに分母の$\beta_n$と打ち消して綺麗になるのですが、分子のディガンマ関数たちは厄介です。そこで、ポリガンマ関数の差の積分表示を利用することで、元の積分を別の積分の和として表してしまおうと思いました。これは一見すると前進していないように思われますが、物は試しです。
\begin{align} \psi\qty(n+\frac12)-\psi(n+1)&=\int_{0}^{1}\frac{x^n-x^{n-\frac12}}{1-x}\d x \\ &=-2\int_{0}^{1}\frac{x^{2n}}{1+x}\d x \\ \psi_1\qty(n+\frac12)-\psi_1(n+1)&=-4\int_{0}^{1}\frac{x^{2n}}{1+x}\ln x\d x \end{align}
これを用いると、
\begin{align} &\frac12\sum_{n=0}^{\infty}\frac{\Gamma(\frac12)\Gamma(n+\frac12)}{(2n+1)\beta_n\Gamma(n+1)}\left[{\left({\psi\qty(n+\frac12)-\psi(n+1)}\right)^2-\left(\psi_1\qty(n+\frac12)-\psi_1(n+1)\right)}\right] \\ &=\frac{\pi}{2} \sum_{n \ge 0} \frac{1}{2n+1} \left[ \left( -2 \int_0^1 \frac{x^{2n}}{1+x} \d x \right)^2 + 4 \int_0^1 \frac{x^{2n} \ln x}{1+x} \d x \right] \\ &= 2\pi \int_0^1 \int_0^1 \frac{\operatorname{artanh}(xy)}{xy(1+x)(1+y)} \d x \d y - 2\pi \int_0^1 \frac{\operatorname{artanh}(x) \ln x}{x(1+x)} \d x \\ &= 2\pi \int_0^1 \frac{1}{y} \int_0^y \frac{\operatorname{artanh}(x)}{x(x+y)} \d x \d y - 2\pi \int_0^1 \frac{\operatorname{artanh} x \ln x}{1-x} \d x \\ &= 2\pi \int_0^1 \operatorname{artanh}(x) \int_x^1 \left( \frac{1}{y(1+y)} - \frac{1}{x+y} \right) \d y \d x - 2\pi \int_0^1 \frac{\operatorname{artanh} x \ln x}{1-x} \d x \\ &= 2\pi \int_0^1 \frac{\operatorname{artanh}(x) \ln\left(\frac{(1+x)^2}{4x}\right)}{x(1-x)} \d x - 2\pi \int_0^1 \frac{\operatorname{artanh} x \ln x}{1-x} \d x \\ &= \pi \int_0^1 \frac{\ln(1-x^2) \ln(x)}{x} \d x - 2\pi \int_0^1 \frac{\operatorname{artanh} x \ln x}{1-x} \d x \\ &= \pi \int_0^1 \frac{\ln(1-x) \ln x}{x} \d x + \pi \int_0^1 \frac{\ln(1+x) \ln x}{x} \d x - \pi \int_0^1 \frac{\ln(1+x) \ln x}{1-x} \d x + \pi \int_0^1 \frac{\ln(1-x) \ln x}{1-x} \d x - 2\pi \int_0^1 \frac{\operatorname{artanh} x \ln x}{1-x} \d x \\ &= 2\pi \int_0^1 \frac{\ln(1-x) \ln x}{x} \d x + \pi \int_0^1 \frac{\ln(1+x) \ln x}{x} \d x + \pi \int_0^1 \frac{\ln(1+x) \ln x}{1-x} \d x - 2\pi \int_0^1 \frac{\ln(1-x) \ln x}{x} \d x　\\ &= 3\pi \int_0^1 \frac{\ln(1-x) \ln x}{x} \d x + \pi \int_0^1 \frac{\ln(1+x) \ln x}{x} \d x \end{align}
(それぞれの変形はここで解説するにはスペースを取りすぎるので省略します。読者への課題ともいう)
重積分を経由して、非常に似通った形の積分が2つ出てきました。確かに問題は解決していないのですが、最初の積分からずいぶん簡単な形になったようです。そしてここまでくればもう計算できることは確信でき、それは$\ln(1-x),\ln(1+x)$に対してテクニック1の級数に変形するを用いればよいわけです。
\begin{align} & 3\pi \int_0^1 \frac{\ln(1-x) \ln x}{x} \d x + \pi \int_0^1 \frac{\ln(1+x) \ln x}{x} \d x \\ &=-3\pi\sum_{n=1}^{\infty}\frac{1}{n}\int_{0}^{1}x^{n}\frac{\ln x}{x}\d x+\pi \sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\int_{0}^{1}x^n\frac{\ln x}{x}\d x\\ &=3\pi\sum_{n=1}^{\infty}\frac{1}{n^3}+\pi\sum_{n=1}^{\infty}\frac{(-1)^n}{n^3} \\ &=3\pi\zeta(3)-\frac{3\pi}{4}\zeta(3)=\frac{9\pi}{4}\zeta(3) \end{align}
計算できました！.....やや回り道をしたように思いますが、実際に私が解いた時の思考を再現しているので最適最速な回答では決してありません。最終的に答えが得られるならば、どんな方法だろうと構わないのです。

かなり圧倒される見た目ですね。答えの$\ln \ln$という項がかなり怪しく見えました。というのも、積分の解として$\ln$が合成されたものは滅多に見ないからです。さらにそのたまに見る場合というのも、大抵は$\ln^{\alpha}$とパラメータをとったものだったり、留数定理の利用だったりしたので、今回の積分もそのような方向で解けるのではないでしょうか。
ひとまずは$\varphi$などで表されている部分を数字に直してしまいます。
\begin{align} &\int_{0}^{\frac\pi2}\frac{\ln(x^2+\ln^2(\cos x))}{1+\frac{\overline{\varphi}^2-1}{\overline{\varphi}^2+1}\cos(2x)}\d x=\frac{\varphi-\overline{\varphi}}{2}\pi\ln\ln\varphi \\ \Longleftrightarrow &\int_{0}^{\frac\pi2}\frac{\ln(x^2+\ln^2(\cos x))}{1-\frac{1}{\sqrt5}\cos(2x)}\d x=\frac{\sqrt5}{2}\pi\ln\ln\varphi \end{align}
$\ln(x^2+\ln^2(\cos x))$という項が厄介そうです。そのため、テクニック4,5をここで活用します。まず、$\ln(x^2+\ln^2(\cos x))=2\Re\ln(\ln\frac{1+e^{2ix}}{2})$です。また、$\ln$という項は中身を底とする指数関数としてパラメータを取ると上手くいくことが多いので、パラメータの微分と見て$\ln\ln(\frac{1+e^{2ix}}{2})=\left.\qty(\ln (\frac{1+e^{2ix}}{2}))^s\right|_{s=0}$とします。
これを踏まえると、元の積分は、
\begin{align} J=\int_{0}^{\frac\pi2}\frac{\ln(x^2+\ln^2(\cos x))}{1-\frac{1}{\sqrt5}\cos(2x)}\d x=2\Re\left.\dfrac{\partial}{\partial s}\int_{0}^{\frac\pi2}\frac{\qty(\ln(\frac{1+e^{2ix}}{2}))^s}{1-\frac{1}{2\sqrt{5}}(e^{2ix}+e^{-2ix})}\d x\right|_{s=0} \end{align}
$e^{2ix}$は明らかに単位円周上の複素積分を思わせるので、分母にある$\cos$もそれにふさわしい形に変形しておきました。
$$I(s)=2\int_{0}^{\frac\pi2}\frac{\qty(\ln(\frac{1+e^{2ix}}{2}))^s}{1-\frac{1}{2\sqrt{5}}(e^{2ix}+e^{-2ix})}\d x=\int_{0}^{\pi}\frac{\qty(\ln(\frac{1+e^{ix}}{2}))^s}{1-\frac{1}{2\sqrt{5}}(e^{ix}+e^{-ix})}\d x$$
とします。
$e^{ix}=z$とした複素積分を考えたいのですが、$ie^{ix}dx=dz$であることから、余分に$e^{ix}$が出てきてしまうのを相殺するため、$I(s)$の分母に$e^{ix}$を掛けておき、それを複素積分の際の被積分関数とします。すなわち、
\begin{align} g(z,s)=\frac{\qty(\ln(\frac{1+z}{2}))^s}{z\qty({1-\frac{1}{2\sqrt5}(z+\frac1z)})} \end{align}
とし、図のように積分経路を取ります。

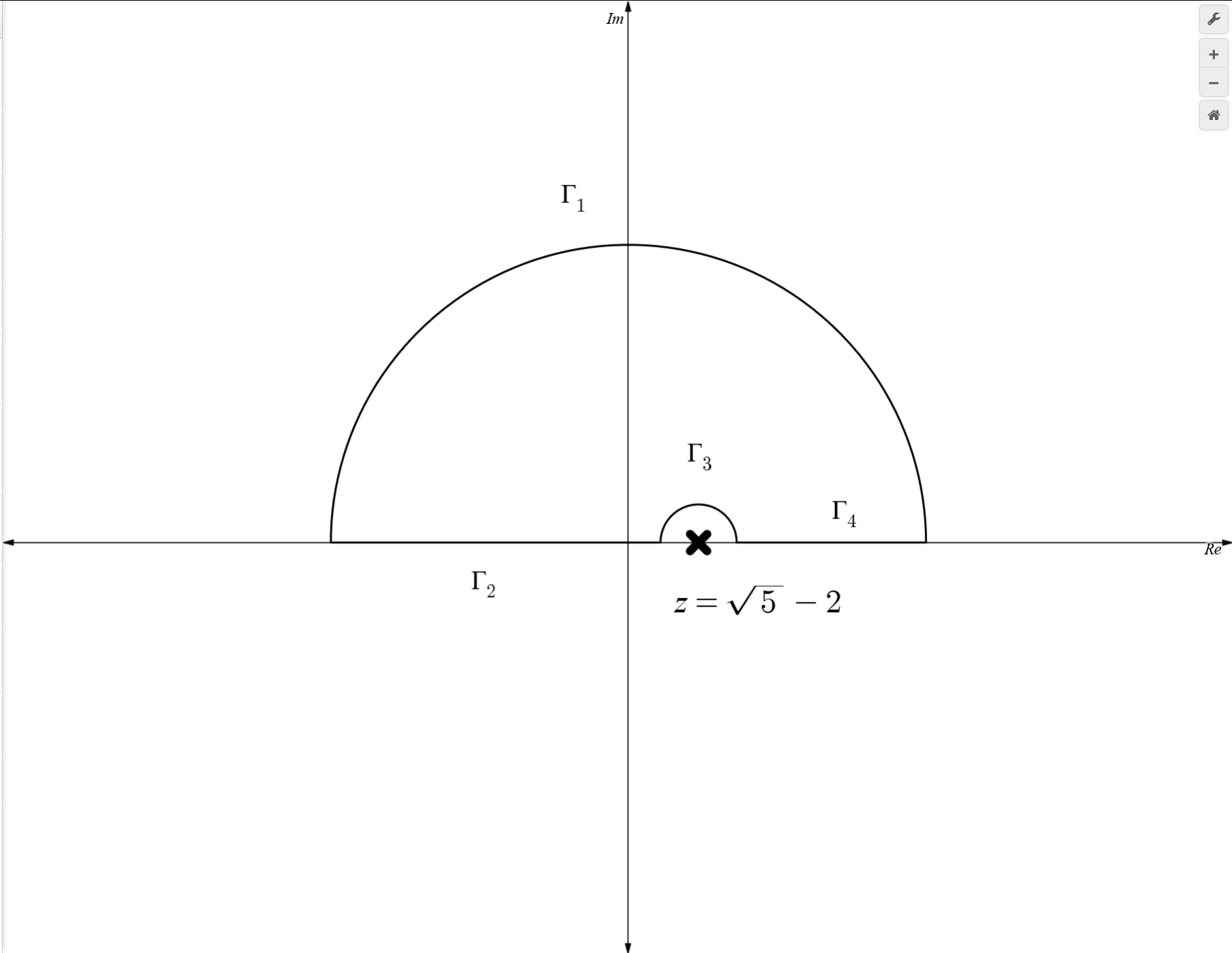
$g(z,s)$は$z=\sqrt{5}-2$に一位の極を持っています。そのため、実軸を動いていく際にその周りを半径$\varepsilon$の小円弧でぐるりと迂回する形で経路を取ります。
ちなみに$\ln(\frac{1+z}{2})$は多価性があるのですが、分枝切断を$z\in(-\infty,-1]$で行っており、今回の積分経路はそれを跨いでいないので問題ありません。ここで$\varepsilon\to0+$の極限を取ると、
\begin{align} &\int_{\Gamma_1}g(z,s)\d z=\int_{0}^{\pi}\frac{\qty(\ln(\frac{1+e^{i\theta}}{2}))^s}{e^{i\theta}\qty(1-\frac{1}{2\sqrt5}\qty(e^{i\theta}+e^{-i\theta}))}ie^{i\theta}\d \theta=iI(s) \\ &\int_{\Gamma_2+\Gamma_4}g(z,s)\d z=\PV\int_{-1}^{1}\frac{\qty(\ln(\frac{1+z}{2}))^s}{z(1-\frac{1}{2\sqrt5}(z+\frac1z))}\d z \\ &\int_{\Gamma_3}g(z,s)\d z=-\frac{1}{2}2\pi i\Res(g(z,s),z=\sqrt5-2)=-\frac{i\pi\sqrt5}{2}\ln(\frac{-1+\sqrt5}{2})^s \end{align}
のようになります。$\Gamma_3$の積分が留数の$-\frac{1}{2}$となっているのは、半周だけ時計回りに回っているためです。よって、
\begin{align} I(s)=i\left[-2\sqrt5\PV\int_{-1}^{1}\frac{\ln(\frac{1+x}{2})^s}{(x-\sqrt5)^2-4}\d x-\frac{i\sqrt5\pi}{2}\ln(\frac{\sqrt5-1}{2})^s\right] \end{align}
です。そもそもの積分は$\Re\dv{I}{s}\left.\right|_{s=0}$でしたので、
\begin{align} J&=\Re\left[-2\sqrt5 i\PV\int_{-1}^{1}\frac{\ln(\ln(\frac{1+x}{2}))}{(x-\sqrt5)^2-4}\d x+\frac{\pi\sqrt5}{2}\ln\ln(\frac{\sqrt5-1}{2})\right] \\ &=\Re\left[\frac{\sqrt5 i}{2}\PV\int_{0}^{1}\frac{\ln\ln x}{x-\frac1\varphi}\d x-\frac{\sqrt5 i}{2}\int_0^{1}\frac{\ln\ln x}{x-\varphi^2}\d x\right]+\frac{\sqrt5 \pi}{2}\ln\ln{\frac1\varphi} \end{align}
です。ただし二つ目の等号では、$(x-\sqrt5)^2-4$を因数分解し、二つの積分に分解し(部分分数分解)たあとに、$\frac{x+1}{2}\to x$の置換をしました。ここで$\ln \ln x$の実部を考えると、$0< x<1$において$\ln x<0$より、$\ln \ln x=i\pi +\ln\ln\frac1x$となります。よって$\Re\ln\ln x=-\pi$と厄介だった$\ln \ln $の部分が消えてしまいました。以上から、
\begin{align} J&=\frac{\sqrt5\pi}{2}\ln\ln\varphi-\frac{\sqrt5 \pi}{2}\PV\int_{0}^{1}\frac{1}{x-\frac1\varphi}\d x+\frac{\sqrt5\pi}{2}\int_{0}^{1}\frac{1}{x-\varphi^2}\d x \\ &=\frac{\sqrt5\pi}{2}\ln\ln\varphi+\frac{\sqrt5\pi}{2}\ln(\frac{\varphi^2}{\varphi^2-1}\cdot\frac{1}{\varphi-1}) \\ &=\frac{\sqrt5\pi}{2}\ln\ln\varphi \end{align}
となります。ただしコーシーの主値積分に関しては、今回の場合$x=\frac1\varphi$の前後で積分を分け、極限を取ればよいです。$\ln\ln x$を含む積分が、実部を取ることで完全に無視できるのは非常に大きいですね。最初から予期していたわけではありませんでしたが、運よくこのアプローチで求めることが出来ました。

多重対数関数が出てきています。多重対数関数は級数展開の形がかなりシンプルな形をしているので、級数展開をすれば計算できそうです。しかし、今回の場合は引数が$1-x^2$となってしまっているので、$\sqrt{1-x^2}\to x$の置換を行い(これは、三角関数に直すと$\sin \theta\to \cos\theta$の置換をすることに相当しています)、そのあとに級数展開をします。
\begin{align} K&=\int_{0}^{1}\frac{\operatorname{Li}_2(1-x^2)}{1-x^2}\d x \\ &=\int_{0}^1\frac{\operatorname{Li}_2(x^2)}{x\sqrt{1-x^2}}\d x \\ &=\sum_{n=1}^{\infty}\frac{1}{n^2}\int_{0}^{1}\frac{x^{2n-1}}{\sqrt{1-x^2}}\d x \\ &=\sum_{n=1}^{\infty}\frac{1}{n^2(2n-1)\beta_{n-1}} \\ &=\frac12\sum_{n=1}^{\infty}\frac{1}{n^3\beta_n} \end{align}
途中でウォリス積分、あるいはベータ関数とガンマ関数の関係式を用いています。また最後の等号では$\beta_n$の漸化式から計算しています。上手くついていけなかった方は、$\beta_n=\frac{\binom{2n}{n}}{2^{2n}}$という関係式から全てをガンマ関数に直して逐次計算していけばこうなることは分かると思います。
さて、積分を級数にでき、さらに比較的性質が良い級数となっています。というのも、分母に$n$がつらなる級数は、ある級数表示をされる関数に$\int\frac1x$という演算を複数回適用することで得られるからです。また、$\arcsin^2x$の級数展開を思い出すと、今回の級数に非常に近い形をしていることに気が付きます。
\begin{align} \arcsin^2x=\frac12\sum_{n=1}^{\infty}\frac{1}{n^2\beta_n}x^{2n} \end{align}
でした。よって、
\begin{align} \frac{1}{2}\sum_{n=1}^{\infty}\frac{1}{n^3\beta_n}&=\frac12\sum_{n=1}^{\infty}\frac{1}{n^2\beta_n}\int_{0}^{1}\frac{x^n}{x}\d x \\ &=\int_{0}^{1}\frac{\arcsin(\sqrt x)^2}{x}\d x \\ &=2\int_{0}^{1}\frac{\arcsin^2 x}{x}\d x \quad(\sqrt x\to x) \\ &=2\int_{0}^{\frac\pi2}x^2\cot x\d x \quad(\arcsin x \to x) \\ &=-4\int_{0}^{\frac\pi2}x\ln(\sin x)\d x\\ &=-4\int_{0}^{\frac\pi2}x\ln(2\sin x)\d x +\frac{\pi^2}2\ln2 \end{align}
となります。$x \ln (\text{三角関数})$という形は問題①でも出てきましたね。この形はFourier展開をして部分積分をすることで級数にできます。ちなみになぜ$\ln$の引数に$2$を加えているかというと、
\begin{align} \ln(2\sin x)=-\sum_{n=1}^{\infty}\frac{\cos(2nx)}{n} \end{align}
とスッキリするからです。よって、
\begin{align} K&=-4\int_{0}^{\frac\pi2}x\ln(2\sin x)\d x +\frac{\pi^2}2\ln2 \\ &=4\sum_{n=1}^{\infty}\frac1n\int_{0}^{\frac\pi2}x\cos(2nx)\d x+\frac{\pi^2}{2}\ln 2 \\ &=\sum_{n=1}^{\infty}\frac{(-1)^n-1}{n^3}+\frac{\pi^2}2\ln 2 \\ &=\frac{\pi^2}{2}\ln2-\frac74\zeta(3) \end{align}
計算できました。積分→級数→積分→級数と変形して何度も同じところをいったりきたり、全然進展していないように見えると思いますが、この行程で段々と見知った形の積分や級数に帰着させていっています。
もっと簡単な解法はあるかもしれませんが、小さなステップを着実に踏んでいき、未知の形を既知に落としていくことで確実に正解に近づくことが出来る場合が多いです。この考え方は問題①、②に共通している解き方でもあるため、積分を解く上で唯一の万能なテクニックといえるかもしれないです。

たった３問のみでしたが、私が積分を解く時にどのような考えで計算をしていくのか、少しでも伝わったでしょうか。この解法を見て、「まどろっこしい」「ああやればもっと簡単に解けるんじゃないか」と感じた方は、競技積分のセンスがあるのでぜひ始めてください。皮肉ではなく、もっと積分界隈が盛り上がればいいな～という思いもあってこの記事を書いたので、積分erを歓迎しています。
ここに挙げた例題は積分の中でもそこそこの難易度に位置するので、まずは各テクニックに設けた演習問題を解いてみて、楽しいなと感じた方はさらに難しい積分にチャレンジしてみると良いと思います。

積分フローチャート

(あとで)

最後に

厳密性をかなぐり捨てて、積分の魅力を伝えることを意識してこの記事を書いたのですが、「積分って面白い！」と思っていただけたでしょうか？　数Ⅲの積分も面白くはあるのですが、高校生の頃の私はいささか物足りなく感じていました。そこから高校範囲を超えた積分の多様でカオスな世界の入り口に触れ、今では四六時中、寝るとき以外は大体積分をしています。非常に複雑な被積分関数が変数変換や変形を繰り返し適用することで見知った形になり、答えが求まることに快感を覚え、また技巧的な解法に圧倒されると同時に他の積分にも適用できないかと考えることもあります。何より、問題を解こうと試行錯誤している時間は知的活動の最たるもので、かけがえのない時間です。SNSやショート動画にうつつを抜かして今日も時間を無駄にしてしまった...と鬱々としているそこのあなた、ぜひこの記事を機に積分を始めてみませんか？　積分が得意になって有用なことはあまりありませんが、ハマると夢中になれる趣味だと思います。

おまけ　よく使う公式・定理集

積分計算、特に非自明な定積分の閉じた解の導出において強力な武器となる主要な公式、定理、テクニックをまとめます。

1. 級数展開・無限積・和公式

基本的な関数のMaclaurin展開

\begin{align} e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \end{align}
($|x| \le 1, x \neq -1$):
\begin{align} \ln(1+x) = \sum_{n=1}^\infty \frac{(-1)^{n-1}}{n} x^n \end{align}
($\alpha \in \mathbb{C}$ , $|x| < 1$):
\begin{align} (1+x)^\alpha = \sum_{n=0}^\infty \binom{\alpha}{n} x^n \end{align}
($|x| < 1$):
\begin{align} \frac{1}{(1-x)^k} = \sum_{n=0}^\infty \binom{n+k-1}{k-1} x^n \end{align}
\begin{align} \arctan(x) = \sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{2n+1} \end{align}
\begin{align} \arcsin(x) = \sum_{n=0}^\infty \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1} = \sum_{n=0}^\infty \frac{\binom{2n}{n}}{4^n (2n+1)} x^{2n+1} \end{align}
\begin{align} (\arcsin x)^2 = \frac{1}{2} \sum_{n=1}^\infty \frac{(2x)^{2n}}{n^2 \binom{2n}{n}} \end{align}
\begin{align} \operatorname{artanh}(x) = \frac{1}{2} \ln\left(\frac{1+x}{1-x}\right) = \sum_{n=0}^\infty \frac{x^{2n+1}}{2n+1} \end{align}

Eulerによるarctanの級数

\begin{align} \arctan(x) = \sum_{n=0}^{\infty} \frac{2^{2n} (n!)^2}{(2n+1)!} \frac{x^{2n+1}}{(1+x^2)^{n+1}} \end{align}

三角・双曲線関数の級数展開（Bernoulli数 $B_n$, Euler数 $E_n$）

\begin{align} \cot(x) = \frac{1}{x} - \sum_{n=1}^\infty \frac{4^n |B_{2n}|}{(2n)!} x^{2n-1} \end{align}
\begin{align} \tan(x) = \sum_{n=1}^\infty \frac{4^n (4^n-1) |B_{2n}|}{(2n)!} x^{2n-1} \end{align}
\begin{align} \sec(x) = \sum_{n=0}^\infty \frac{(-1)^n E_{2n}}{(2n)!} x^{2n} \end{align}
\begin{align} \csc(x) = \frac{1}{x} + \sum_{n=1}^\infty \frac{(2^{2n}-2) |B_{2n}|}{(2n)!} x^{2n-1} \end{align}

部分分数展開 (Mittag-Leffler Expansion)

\begin{align} \pi \cot(\pi z) = \frac{1}{z} + \sum_{n=1}^\infty \frac{2z}{z^2 - n^2} \end{align}
\begin{align} \frac{\pi}{\sin(\pi z)} = \frac{1}{z} + \sum_{n=1}^\infty \frac{(-1)^n 2z}{z^2 - n^2} \end{align}
\begin{align} \frac{\pi^2}{\sin^2(\pi z)} = \sum_{n=-\infty}^\infty \frac{1}{(z-n)^2} \end{align}

無限積展開 (Weierstrass Factorization)

\begin{align} \frac{\sin(\pi z)}{\pi z} = \prod_{n=1}^\infty \left( 1 - \frac{z^2}{n^2} \right) \end{align}
\begin{align} \cos(\pi z) = \prod_{n=1}^\infty \left( 1 - \frac{4z^2}{(2n-1)^2} \right) \end{align}
\begin{align} \frac{1}{\Gamma(z)} = z e^{\gamma z} \prod_{n=1}^\infty \left( 1 + \frac{z}{n} \right) e^{-z/n} \end{align}

Euler-Maclaurinの和公式 (Euler-Maclaurin Formula)

\begin{align} \sum_{k=m}^n f(k) \approx \int_m^n f(x) \d x + \frac{f(m)+f(n)}{2} + \sum_{k=1}^{\lfloor p/2 \rfloor} \frac{B_{2k}}{(2k)!} (f^{(2k-1)}(n) - f^{(2k-1)}(m)) \end{align}

2. Fourier展開 (Fourier Series)

複素Fourier級数

周期 $T$ の関数 $f(t)$：
\begin{align} f(t) = \sum_{n=-\infty}^\infty c_n e^{i n \omega_0 t} \quad (\omega_0 = 2\pi/T) \end{align}
\begin{align} c_n = \frac{1}{T} \int_{-T/2}^{T/2} f(t) e^{-i n \omega_0 t} \d t \end{align}

展開例（周期 $2\pi$）

のこぎり波 $f(x) = x$ ($-\pi < x < \pi$):
\begin{align} f(x) = 2 \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} \sin(nx) \end{align}
$f(x) = x^2$ ($-\pi < x < \pi$):
\begin{align} f(x) = \frac{\pi^2}{3} + 4 \sum_{n=1}^\infty \frac{(-1)^n}{n^2} \cos(nx) \end{align}
Poisson核 ($0 \le r < 1$):
\begin{align} P_r(\theta) = \frac{1-r^2}{1-2r\cos\theta+r^2} = \sum_{n=-\infty}^\infty r^{|n|} e^{i n \theta} \end{align}

特殊関数の展開例

Clausen関数 (周期 $2\pi$):
\begin{align} \operatorname{Cl}_2(\theta) = \sum_{n=1}^\infty \frac{\sin(n\theta)}{n^2} \end{align}
\begin{align} \operatorname{Cl}_{2m}(\theta) = \sum_{n=1}^\infty \frac{\sin(n\theta)}{n^{2m}} \end{align}
\begin{align} \operatorname{Cl}_{2m+1}(\theta) = \sum_{n=1}^\infty \frac{\cos(n\theta)}{n^{2m+1}} \end{align}
対数正弦・余弦 (Log-sine/cosine) ($0 < x < 2\pi$):
\begin{align} \ln\left(2\sin\frac{x}{2}\right) = - \sum_{n=1}^\infty \frac{\cos(nx)}{n} \end{align}
($-\pi < x < \pi$):
\begin{align} \ln\left(2\cos\frac{x}{2}\right) = \sum_{n=1}^\infty \frac{(-1)^{n-1}}{n} \cos(nx) \end{align}
($0 < x < 1$):
\begin{align} \ln(\sin(\pi x)) = -\ln 2 - \sum_{n=1}^\infty \frac{\cos(2\pi n x)}{n} \end{align}
Bernoulli多項式 (周期 $1$, $0 \le x \le 1$):
\begin{align} B_n(x) = - \frac{n!}{(2\pi i)^n} \sum_{k \neq 0} \frac{e^{2\pi i k x}}{k^n} \end{align}
\begin{align} B_{2m}(x) = 2(-1)^{m+1} (2m)! \sum_{k=1}^\infty \frac{\cos(2\pi k x)}{(2\pi k)^{2m}} \end{align}
\begin{align} B_{2m+1}(x) = 2(-1)^{m+1} (2m+1)! \sum_{k=1}^\infty \frac{\sin(2\pi k x)}{(2\pi k)^{2m+1}} \end{align}

3. 積分変換 (Integral Transforms)

Fourier変換 (Fourier Transform)

\begin{align} \mathcal{F}[f](\xi) = \hat{f}(\xi) = \int_{-\infty}^\infty f(x) e^{-i \xi x} \d x \end{align}
反転公式:
\begin{align} f(x) = \frac{1}{2\pi} \int_{-\infty}^\infty \hat{f}(\xi) e^{i \xi x} \d \xi \end{align}
Plancherelの定理:
\begin{align} \int_{-\infty}^\infty |f(x)|^2 \d x = \frac{1}{2\pi} \int_{-\infty}^\infty |\hat{f}(\xi)|^2 \d \xi \end{align}

Laplace変換 (Laplace Transform)

\begin{align} \mathcal{L}[f](s) = F(s) = \int_0^\infty f(t) e^{-st} \d t \end{align}

Maz's Identity ($F(s)=\mathcal{L}[f](s), G(s)=\mathcal{L}[g](s)$):
\begin{align} \int_{0}^{\infty} F(x) g(x) \d x = \int_{0}^{\infty} f(x) G(x) \d x \end{align}

Mellin変換 (Mellin Transform)

\begin{align} \mathcal{M}[f](s) = \phi(s) = \int_0^\infty f(x) x^{s-1} \d x \end{align}
反転公式:
\begin{align} f(x) = \frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty} \phi(s) x^{-s} \d s \end{align}

4. 解析学の重要定理

留数定理 (Residue Theorem)

\begin{align} \oint_C f(z) \d z = 2\pi i \sum_{k} \operatorname{Res}(f, a_k) \end{align}

Poissonの和公式 (Poisson Summation Formula)

\begin{align} \sum_{n=-\infty}^\infty f(n) = \sum_{k=-\infty}^\infty \hat{f}(k) \end{align}

Abel-Planaの和公式 (Abel-Plana Formula)

\begin{align} \sum_{n=0}^\infty f(n) = \int_0^\infty f(x) \d x + \frac{f(0)}{2} + i \int_0^\infty \frac{f(iy) - f(-iy)}{e^{2\pi y} - 1} \d y \end{align}

5. 調和数 (Harmonic Numbers)

定義

\begin{align} H_n = \sum_{k=1}^n \frac{1}{k} \end{align}

積分表示

\begin{align} H_n = \int_0^1 \frac{1-x^n}{1-x} \d x \end{align}

母関数

\begin{align} \sum_{n=1}^\infty H_n z^n = \frac{-\ln(1-z)}{1-z} \end{align}

Digamma関数との関係

\begin{align} H_n = \psi(n+1) + \gamma \end{align}

6. 特殊関数と関連公式

Gamma関数 (Gamma Function)

Eulerの積分表示 ($\operatorname{Re}(z) > 0$):
\begin{align} \Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \d t \end{align}
相反公式:
\begin{align} \Gamma(z)\Gamma(1-z) = \frac{\pi}{\sin(\pi z)} \end{align}
Raabeの公式 ($a \ge 0$):
\begin{align} \int_a^{a+1} \ln \Gamma(z) \d z = \frac{1}{2} \ln(2\pi) + a \ln a - a \end{align}

Beta関数 (Beta Function)

第一種Euler積分:
\begin{align} B(x, y) = \int_0^1 t^{x-1} (1-t)^{y-1} \d t = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)} \end{align}
三角関数表示:
\begin{align} B(x, y) = 2 \int_0^{\pi/2} (\sin \theta)^{2x-1} (\cos \theta)^{2y-1} \d \theta \end{align}
無限区間での表示:
\begin{align} B(x, y) = \int_0^\infty \frac{t^{x-1}}{(1+t)^{x+y}} \d t \end{align}

Digamma関数とPolygamma関数

定義:
\begin{align} \psi(z) = \frac{d}{dz} \ln \Gamma(z) = \frac{\Gamma'(z)}{\Gamma(z)} \end{align}
積分表示:
\begin{align} \psi(z) = \int_0^\infty \left( \frac{e^{-t}}{t} - \frac{e^{-zt}}{1-e^{-t}} \right) \d t \end{align}
差の積分表示:
\begin{align} \psi(x) - \psi(y) = \int_0^\infty \frac{e^{-yt} - e^{-xt}}{1-e^{-t}} \d t \end{align}

Riemannゼータ関数 (Riemann Zeta Function)

積分表示:
\begin{align} \zeta(s) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{x^{s-1}}{e^x-1} \d x \end{align}

多重対数関数 (Polylogarithm)

定義:
\begin{align} \operatorname{Li}_s(z) = \sum_{k=1}^\infty \frac{z^k}{k^s} \end{align}
関係式:
\begin{align} \int_0^z \frac{\operatorname{Li}_s(t)}{t} \d t = \operatorname{Li}_{s+1}(z) \end{align}

指数積分 (Exponential Integral)

\begin{align} E_1(x) = \int_x^\infty \frac{e^{-t}}{t} \d t \end{align}
\begin{align} \operatorname{Ei}(x) = \text{p.v.} \int_{-\infty}^x \frac{e^t}{t} \d t \end{align}

対数積分 (Logarithmic Integral)

\begin{align} \operatorname{li}(x) = \int_0^x \frac{\d t}{\ln t} \end{align}

三角積分 (Trigonometric Integrals)

\begin{align} \operatorname{Si}(x) = \int_0^x \frac{\sin t}{t} \d t \end{align}
\begin{align} \operatorname{Ci}(x) = -\int_x^\infty \frac{\cos t}{t} \d t \end{align}

7. 楕円積分 (Elliptic Integrals)

パラメータ $k$ は母数 (modulus)、$\phi$ は振幅 (amplitude) を表す。

第一種不完全楕円積分

\begin{align} F(\phi, k) = \int_0^\phi \frac{\d \theta}{\sqrt{1-k^2 \sin^2 \theta}} \end{align}

第一種完全楕円積分

\begin{align} K(k) = F\left(\frac{\pi}{2}, k\right) = \int_0^{\pi/2} \frac{\d \theta}{\sqrt{1-k^2 \sin^2 \theta}} \end{align}

第二種不完全楕円積分

\begin{align} E(\phi, k) = \int_0^\phi \sqrt{1-k^2 \sin^2 \theta} \d \theta \end{align}

第二種完全楕円積分

\begin{align} E(k) = E\left(\frac{\pi}{2}, k\right) = \int_0^{\pi/2} \sqrt{1-k^2 \sin^2 \theta} \d \theta \end{align}

第三種不完全楕円積分 (特性 $n$)

\begin{align} \Pi(n; \phi, k) = \int_0^\phi \frac{\d \theta}{(1-n \sin^2 \theta) \sqrt{1-k^2 \sin^2 \theta}} \end{align}

特殊値・関係式

Legendreの恒等式 ($k' = \sqrt{1-k^2}$ は補母数):
\begin{align} K(k)E(k') + E(k)K(k') - K(k)K(k') = \frac{\pi}{2} \end{align}
基本値:
\begin{align} K(0) = \frac{\pi}{2}, \quad E(0) = \frac{\pi}{2} \end{align}
\begin{align} K(1) = \infty, \quad E(1) = 1 \end{align}
特異母数 (Lemniscate):
\begin{align} K\left(\frac{1}{\sqrt{2}}\right) = \frac{\Gamma(1/4)^2}{4\sqrt{\pi}} \end{align}

8. 主要な数学定数

Euler-Mascheroni定数 $\gamma$

\begin{align} \gamma = \lim_{n \to \infty} \left( \sum_{k=1}^n \frac{1}{k} - \ln n \right) = - \psi(1) \end{align}
\begin{align} \gamma = \int_0^\infty \left( \frac{1}{e^t-1} - \frac{1}{t e^t} \right) \d t \end{align}

Apéryの定数 $\zeta(3)$

\begin{align} \zeta(3) = \sum_{n=1}^\infty \frac{1}{n^3} = \frac{1}{2} \int_0^1 \int_0^1 \frac{-\ln(xy)}{1-xy} \d x \d y \end{align}

Catalanの定数 $G$

\begin{align} G = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^2} = \int_0^1 \frac{\arctan x}{x} \d x \end{align}

9. 種々の積分公式とテクニック

Leibnizの積分法則 (Feynman's Technique)

\begin{align} \frac{d}{dt} \int_{a(t)}^{b(t)} f(x, t) \d x = f(b(t), t) \frac{db}{dt} - f(a(t), t) \frac{da}{dt} + \int_{a(t)}^{b(t)} \frac{\partial}{\partial t} f(x, t) \d x \end{align}

Frullaniの積分 (Frullani Integral)

$f(0)$ と $f(\infty) = \lim_{x\to\infty} f(x)$ が存在するとき：
\begin{align} \int_0^\infty \frac{f(ax) - f(bx)}{x} \d x = (f(0) - f(\infty)) \ln \frac{b}{a} \end{align}

Glasser's Master Theorem

\begin{align} \int_{-\infty}^\infty f\left(x - \frac{a}{x}\right) \d x = \int_{-\infty}^\infty f(y) \d y \end{align}

Ramanujan's Master Theorem

$f(x) = \sum_{k=0}^\infty \frac{\phi(k)}{k!} (-x)^k$ のとき：
\begin{align} \int_0^\infty x^{s-1} f(x) \d x = \Gamma(s) \phi(-s) \end{align}

Lobachevskyの積分公式

$f(x)$ が連続関数で、$f(x+\pi) = f(x)$ と $f(\pi-x) = f(x)$ を満たすとき：
\begin{align} \int_0^\infty \frac{\sin x}{x} f(x) \d x = \int_0^{\pi/2} f(x) \d x \end{align}