PCP定理とその証明 (証明概要編)

248

本記事は

の続きで, PCP定理の証明の全体像を説明します. 細かい解析などは後の記事で行います. この分野を専門的に学ぶ必要がない限りは本記事まで把握していれば良いと思います. 「エクスパンダー性がどのように効いてくるのか？」などについては以降の記事を読む必要があります.

PCP定理

ある定数$c>0,k\in\mathbb{N}$, 多項式$p\colon\Nat\to\Nat$, 有限集合$\Sigma_0$と, 与えられた2-CSPのインスタンス$\mathcal{C}$を以下の性質を満たす別の2-CSPのインスタンス$\mathcal{C}'$に変換する多項式時間アルゴリズムが存在する: 任意の2-CSPインスタンス$\mathcal{C}$に対し,

$\UNSAT(\mathcal{C})=0 \Rightarrow \mathrm{UNSAT}(\mathcal{C}')=0$
$\mathrm{UNSAT}(\mathcal{C})>0 \Rightarrow \mathrm{UNSAT}(\mathcal{C}')\geq c$
$\mathcal{C}$の変数の個数を$n$とすると, $\mathcal{C}'$の変数の個数は高々$p(n)$.
$\mathcal{C}'$のアルファベットは$\Sigma_0$.

簡単な復習

これまで, 2-CSPに対して制約グラフと呼ばれる概念を定義しました.

2-CSPの制約グラフ(前回の記事の定義2の再掲)

以下を満たす$G=((V,E),\Sigma,\mathcal{C})$を制約グラフと呼ぶ:

$(V,E)$は構造グラフと呼ばれる無向グラフであり, $V$は変数の集合に対応する. 頂点集合$V$は$V=\{v_1,\dots,v_n\}$などと番号付けされており, それに基づいて順序が定まっている.
$\Sigma$は有限集合であり, アルファベットと呼ばれる. 変数には$\Sigma$の要素が代入される.
各辺$e\in E$には制約と呼ばれる集合$c(e)\subseteq \Sigma\times \Sigma$が対応しており, $(a,b)\in\Sigma\times\Sigma$が$(a,b)\in c(e)$を満たすとき, $(a,b)$は制約$c(e)$を満たすという.

関数$\sigma\colon V\to \Sigma$を割当といい,
$$ \UNSAT(G,\sigma)=\frac{|\{uv\in E\colon (\sigma(u),\sigma(v))\not\in c(uv)\}|}{|E|} $$
を割当$\sigma$によって充足されない制約の割合とし, $\UNSAT(G)=\min\{\UNSAT(G,\sigma)\colon \sigma\in \Sigma^V\}$とする. ここで$\{u,v\}$は$u$が$v$よりも($V$上の順序の意味で)前にあり$(\sigma(u),\sigma(v))$を順序対として扱っている.

制約グラフ$G = ((V,E),\Sigma,\mathcal{C})$のサイズを
$$ \mathrm{size}(G) = |V|+|E| $$
で定めます ($\Sigma$と$\mathcal{C}$には依存しません).

ステップ1ではUNSATの値をさほど変えずに構造グラフを正則エクスパンダーに変換できることを示しました.

(前回の記事の定理4の再掲)

ある定数$\lambda<1,d\in\Nat,c>0,\beta>0$が存在して, 任意の制約グラフ$G=((V,E),\Sigma,\mathcal{C})$が与えられたときに以下の性質を満たす制約グラフ$G'=((V',E'),\Sigma,\mathcal{C}')$を出力する決定的多項式時間アルゴリズムが存在する:

$(V',E')$は自己ループを持つ$d$-正則な$\lambda$-エクスパンダー.
$|V'|\leq c|E|$.
$\UNSAT(G)\geq \UNSAT(G')\geq \beta\cdot \UNSAT(G)$.

以後, 簡単のためにグラフに対する諸概念を制約グラフに対して当てはめて呼びます. 例えば「$d$-正則制約グラフ」と言った場合, その構造グラフ$(V,E)$の正則性を意味します.

UNSATの倍化

定理1はUNSATの値を倍化するという次の定理から証明できます.

ある有限集合$\Sigma_0$が存在して次が成り立つ: 任意のアルファベット$\Sigma$に対してある二つの定数$c>0,0<\alpha<1$が存在して, 与えられた制約グラフ$G=((V,E),\Sigma,\mathcal{C})$に対して多項式時間で別の制約グラフ$G'=((V',E'),\Sigma_0,\mathcal{C}')$が構成できて以下の三つの条件を満たす:

$\mathrm{size}(G') \le c\cdot \mathrm{size}(G)$
$\mathrm{UNSAT}(G)=0$ならば$\mathrm{UNSAT}(G')=0$
$\mathrm{UNSAT}(G') \ge \min(\alpha, 2\cdot \mathrm{UNSAT}(G)))$

端的に言えば, 制約グラフをUNSAT値を倍になるよう効率的に変換できるという定理です. 充足不能な制約グラフ$G$は常に$\mathrm{UNSAT}(G) \ge 1/|E|$が成り立つので, ギャップ増幅定理を$O(\log(|E|))$回だけ適用すれば$\mathrm{UNSAT}(G)\ge \alpha$にできます.

(定理3を仮定した上で定理1を証明)

与えられた2-CSPのインスタンスを表す制約グラフ$G$に対して定理3を$i$回適用して得られる制約グラフを$G_i$とする. すなわち, $G_0=G$とし, $G_i$に定理3を適用して構成される制約グラフを$G_{i+1}$と定義する.

各$G_i$はアルファベット$\Sigma_0$上の2-CSPであり, $\UNSAT(G_i) \ge \min(2^i/|E|,\alpha)$なので, $i = \lceil \log_2(|E|) \rceil$に対して$\UNSAT(G_i) \ge \alpha$となります. この定数$\alpha$はアルファベット$\Sigma_0$にのみ依存するのでuniversal constantとすることができる.　また, $\mathrm{size}(G_i) \le c^i\cdot \mathrm{size}(G) \le \mathrm{poly}(\mathrm{size}(G))$である.
従ってこの$G_i$に対応する2-CSPは定理1の主張を確かに満たす.

定理3の証明は次の三つの構成要素からなります:

構造グラフをスパースかつエクスパンダーにする
ギャップ増幅
アルファベット削減

前回の記事では一つ目について解説しました. 本記事では残りの二つについて解説します.

ギャップ増幅補題

定理3の証明へのチャレンジとして, 次の方針を考えてみます.

方針: アルファベットの増大

アルファベットサイズを(元の制約グラフのサイズに依存して)十分大きくすることが許されるならば, ギャップ増幅は容易です. 元の制約グラフを$G=((V,E),\Sigma,\mathcal{C})$とします. $G'=((V,E'),\Sigma',\mathcal{C}')$を以下で定めます:

変換後のグラフ$(V,E')$を$V$上の完全グラフとします.
変換後のアルファベットを$\Sigma'=\Sigma^V$とします. 割り当て$\sigma \colon V \to \Sigma'$と頂点$u\in V$に対し, $\sigma(u) \in \Sigma'$は関数$\sigma(u) \colon V \to \Sigma$とみなします.
変換後の制約$\mathcal{C}'$を定義します. 割り当て$\sigma \colon V \to \Sigma'$は次の条件を満たすとき, $G'$の辺$e=\{u,v\}$における制約を満たすとします: 関数として$\sigma(u)=\sigma(v)$であり, さらに$\sigma(u)\colon V \to \Sigma$は元の制約グラフの$\mathcal{C}$の全ての制約を満たす.

元の制約グラフ$G$が$\UNSAT(G)=0$ならば, その充足割り当てを使って$G'$の充足割り当てが構成できるため$\UNSAT(G')=0$です. 一方で$\UNSAT(G)>0$ならば, どの割り当てを使っても全ての辺が充足されないため$\UNSAT(G')=1$となります. 完全グラフに変換する方法は確かにギャップを増幅しています.

しかしこの構成は定理3の証明にはなりえません. というのも, この構成によって得られる制約グラフのアルファベット$\Sigma'=\Sigma^V$はその要素数が元のグラフに依存してしまうからです. 定理3では, 元のグラフが如何に大きくても同じアルファベット$\Sigma_0$上の制約グラフに変換することが要請されていることに注意が必要です.

制約グラフの冪乗

ギャップ増幅ではグラフの冪乗と呼ばれる操作によって与えられる制約グラフを考えます. 一般にグラフの冪乗と言えばそのグラフの隣接行列の冪乗を指す概念です. グラフ$G = (V,E)$および$\ell\in \mathbb{Z}_{\ge 0}$に対し, $\ell+1$個の頂点からなる列$(u_0,u_1,\dots,u_\ell)$は全ての$u_i,u_{i+1}$が辺をなすときに$u_0$から$u_\ell$への$\ell$-ウォークと呼び, 特に二頂点$u_0,u_\ell$をそれぞれ始点,終点と呼びます. ここでは$(u_0,\dots,u_\ell)$は順序付きのタプルですが, グラフは無向グラフなので順序を反転させたタプル$(u_\ell,\dots,u_0)$もまた$u_\ell$から$u_0$への$\ell$-ウォークになっています.

冪乗グラフ$G^\ell$とは全ての長さ$\ell$のウォークの端点間に辺を追加して得られるグラフです. 同じ二頂点間に長さ$t$のウォークが二通り以上存在する場合はその個数(逆向きのウォークは数えない)分だけ多重辺にします. 元のグラフ$G$が$d$-正則ならば$G^\ell$は$d^\ell$-正則です (ここでは多重辺はその分だけ次数をカウントしているため, 隣接点がちょうど$d^\ell$個あるわけではないことに注意).
グラフ!FORMULA[124][36833][0]と!FORMULA[125][35453837][0]の例. 太線は2本の多重辺を持つことを意味する. グラフ$G$と$G^2$の例. 太線は2本の多重辺を持つことを意味する.

制約グラフに対する冪乗操作を定めるためにいくつか準備をします. $d$-正則な制約グラフ$G$を考え, その頂点集合$V$に番号付けをして$V=\{v_1,\dots,v_n\}$とし, $V$に全順序をつけます (このときの順序はどのようなものでも構いません). このとき, 各頂点$u$の隣接点集合$N_G(u)$にも頂点番号に基づいて順序が定まります. こうすることで, 頂点$u$の$j$番目の隣接点を定めることができます. 同様に$G^\ell$に対しても$u$の隣接頂点集合$N_{G^\ell}(u)$に順序がつきます.

次の定義がこの記事(ひいてはDinur PCPの理解)における最も重要な概念ですので, 長いですが確実に理解しましょう.

(制約グラフの冪乗)

$d$-正則な制約グラフ$G=((V,E),\Sigma,\mathcal{C})$と$t\in \Nat$に対し, 制約グラフ$G^t = ((V,E'),\Sigma',\mathcal{C}')$を以下で定義する:

グラフ$(V,E')$は冪乗$(V,E')=(V,E)^t$で定める. 記法の単純化のため, 以下では$\Gamma(u) = N_{G^{\lceil t/2 \rceil}}(u)$とする.
アルファベット$\Sigma'$は$\Sigma' = \Sigma^{d^{\lceil t/2 \rceil}}$. 割り当て$\vec{\sigma}\colon V\to \Sigma'$に対し, 各$\vec{\sigma}(u)=(a_1,\dots,a_{d^{\lceil t/2 \rceil}})\in \Sigma^{d^{\lceil t/2 \rceil}}$を関数$\vec{\sigma}(u)\colon \Gamma(u) \to \Sigma$に対応させる. この関数は$\Gamma(u)$の$i$番目の頂点に$a_i \in \Sigma$を割り当てる関数である. なお, $i>|\Gamma(u)|$に対して$a_i$はこの対応関係に影響しないので, 一対一対応関係ではない. 頂点$v \in \Gamma(u)$に割り当てられた値を$\vec{\sigma}(u)_v$とし, これを$u$の$v$に対する意見と呼ぶ.
$G'$の各辺$e'=\{u,v\} \in E'$の制約は, 二頂点$u,v$の値$a,b \in \Sigma'$が次の条件を満たすかつその時に限り, $(a,b)$は$e'$の制約を満たすとする: 任意の$\{\tilde{u},\tilde{v}\}\in E$を満たす$\tilde{u} \in \Gamma(u), \tilde{v} \in \Gamma(v)$に対し, $(a_{\tilde{u}}, b_{\tilde{v}}) \in \Sigma^2$が元のグラフの制約$c(\{\tilde{u},\tilde{v}\})$を満たす.

初見だとイメージがわかりずらいかもしれませんが, 次の図が参考になると思います.
頂点!FORMULA[169][38259][0]に割り当てられた値!FORMULA[170][37639][0]は!FORMULA[171][-404021683][0]の各頂点に!FORMULA[172][838988151][0]の元を割り当てる関数とみなす (上). それぞれ頂点!FORMULA[173][36778281][0]を中心とした距離!FORMULA[174][-1912477639][0]にある二つの円を考え, それらの間にある!FORMULA[175][36833][0]の辺に対応する制約を全て満たしていれば, !FORMULA[176][-1173451986][0]は!FORMULA[177][-393664998][0]に対応する制約を満たす. 頂点$u$に割り当てられた値$a$は$\Gamma(u)=N_{G^{\lceil t/2 \rceil}}(u)$の各頂点に$\Sigma$の元を割り当てる関数とみなす (上). それぞれ頂点$u,v$を中心とした距離$\lceil t/2 \rceil$にある二つの円を考え, それらの間にある$G$の辺に対応する制約を全て満たしていれば, $(a,b)$は$e'=\{u,v\}$に対応する制約を満たす.

$G^t$の辺$e=\{u,v\}$は長さ$t$のウォークの端点であり, 制約$\mathcal{C}'$の構成では半径$\lceil t/2 \rceil$の円を考えているので, 必ず二つの円は(幾何的な意味での)交わりを持ちます. しかし一般に円上の二点の間に必ずしも辺があるとは限りません(その場合は辺$e'$は任意の割り当てで充足されると定義します).

実際には, 前処理として補題2を適用して構造グラフを自己ループ付きのエクスパンダーに変換してから冪乗操作を行います. 従って(長さ$\lceil t/2\rceil$のウォークは自己ループもとりうるので)実際には長さ$\lceil t/2 \rceil$以下のウォークを全て考えるため, 円上でというよりは球上の頂点を考える方がイメージとしては適切です.

元の制約グラフが$\UNSAT(G)=0$ならば, $\UNSAT(G^t)=0$です. 実際, $G$の充足割り当ての一つを$\sigma\colon V \to \Sigma$としたときに, $\vec{\sigma}(u)_v = \sigma(v)$なる任意の$\vec{\sigma}$を考えると球内の任意の二頂点間の元の制約が満たされるため, $\UNSAT(G^t)=0$となることがわかります.

では$\UNSAT(G)>0$であった時はどうなるでしょうか? 元の制約グラフ$G$が自己ループを持つ正則エクスパンダーならば$\UNSAT(G^t)$が増幅することが示せます.

(ギャップ増幅補題)

$\lambda,d,|\Sigma|$を任意の定数とする. これら三つのみに依存するある定数$\beta=\beta(\lambda,d,|\Sigma|)>0$が存在して以下が成り立つ: $d$-正則$\lambda$-エクスパンダーである任意の制約グラフ$G=((V,E),\Sigma,\mathcal{C})$に対し,
$$ \UNSAT(G^t) \ge \beta\sqrt{t}\cdot \min\left( \UNSAT(G), \frac{1}{t} \right). $$

アルファベット削減

パラメータ$t\in\Nat$を$2/\beta$くらいにとっておけば補題4より$\UNSAT(G^t)\ge 2\UNSAT(G)$となります. 一見するとこれで定理3を示せていそうに見えますが,　$G^t$のアルファベット$\Sigma'$はその要素数が元のアルファベット$\Sigma$に依存してしまうため証明になっていません. そこでアルファベットサイズを$G$に依存しない定数まで削減する必要があります. このパートをアルファベット削減(alphabet reduction)と言います.

(アルファベット削減補題)

あるアルファベット$\Sigma_0$と二つの定数$\beta,c>0$が存在して次が成り立つ:
任意の制約グラフ$G=((V,E),\Sigma,\mathcal{C})$を多項式時間で別の制約グラフ$G'=((V',E'),\Sigma_0,\mathcal{C}')$に変換できて$G'$は以下を満たす:

$\mathrm{size}(G') \le c\cdot \mathrm{size}(G)$.
$\beta\cdot \UNSAT(G) \le \UNSAT(G') \le \UNSAT(G)$

ここではアルファベット$\Sigma_0$と定数$\beta,c$は与えられた制約グラフ$G$に依存しないことに注意してください.
補題5は当時すでに知られていた手法から(専門家にとっては)容易に証明できる内容なのですが, その証明には誤り訂正符号やassignment tester (PCP of proxity) といった概念を要するので初学者にとっては厳しい道のりになるでしょう.

各種補題の仮定の下でのPCP定理の証明

エクスパンダー化(補題2), ギャップ増幅補題(補題4), アルファベット削減補題(補題5)の仮定の下で定理3を証明します. 定理3がPCP定理(定理1)を導出することは既に示してありますので, これらの補題からPCP定理が導出できます.

(補題2,4,5$\Rightarrow$定理3)

与えられた制約グラフを$G = ((V,E),\Sigma,\mathcal{C})$とする.
下図のように補題2,4,5をこの順に適用して制約グラフを変換していく.
ギャップ増幅補題を適用する際のパラメータ$t$はあとで適切に設定する.
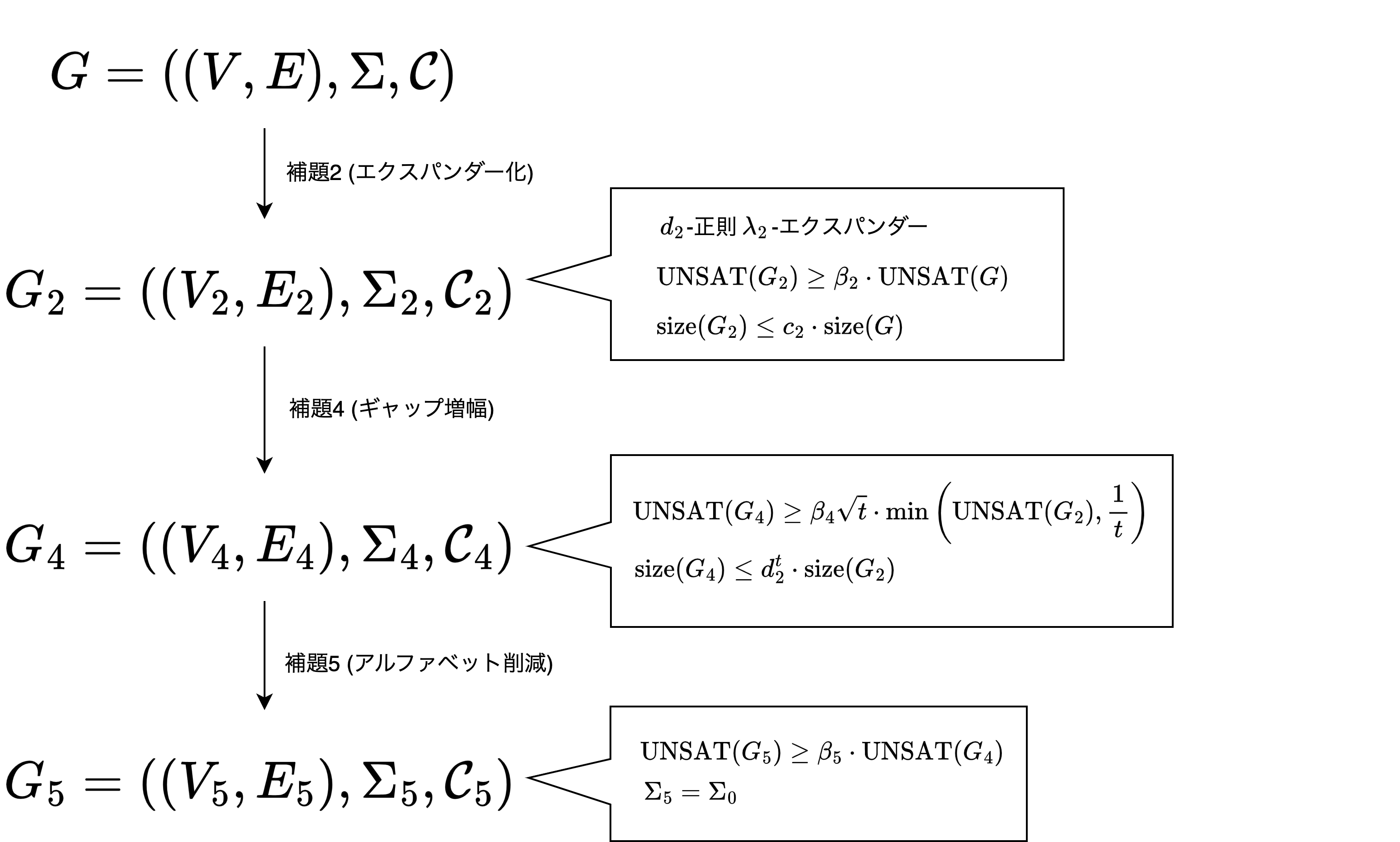補題2,4,5を適用して制約グラフを変換していく.
この一連の変換では, $\UNSAT(G)=0$ならば$\UNSAT(G_5)=0$であることは容易に確認できます.
ギャップ増幅補題(補題4)を適用する際, パラメータ$t$を$t = \frac{4}{(\beta_5\beta_4\beta_2)^2}$とすると, 最終的に得られる制約グラフ$G_5$は
\begin{align*} \UNSAT(G_5) &\ge \beta_5\cdot \UNSAT(G_4) \\ &\ge \beta_5\cdot \beta_4 \sqrt{t} \cdot \min\left( \UNSAT(G_2),\frac{1}{t} \right) \\ &\ge \beta_5\cdot \beta_4 \sqrt{t} \cdot \min\left( \beta_2\UNSAT(G),\frac{1}{t} \right) \\ & \ge 2\min\left( \UNSAT(G),\frac{1}{t} \right) \end{align*}
となる. 従って, $\alpha = 2/t$とすれば定理3の$\UNSAT(G')$に関する主張を満たすことになる. なお, 各パラメータの従属関係を図示すると以下となる:
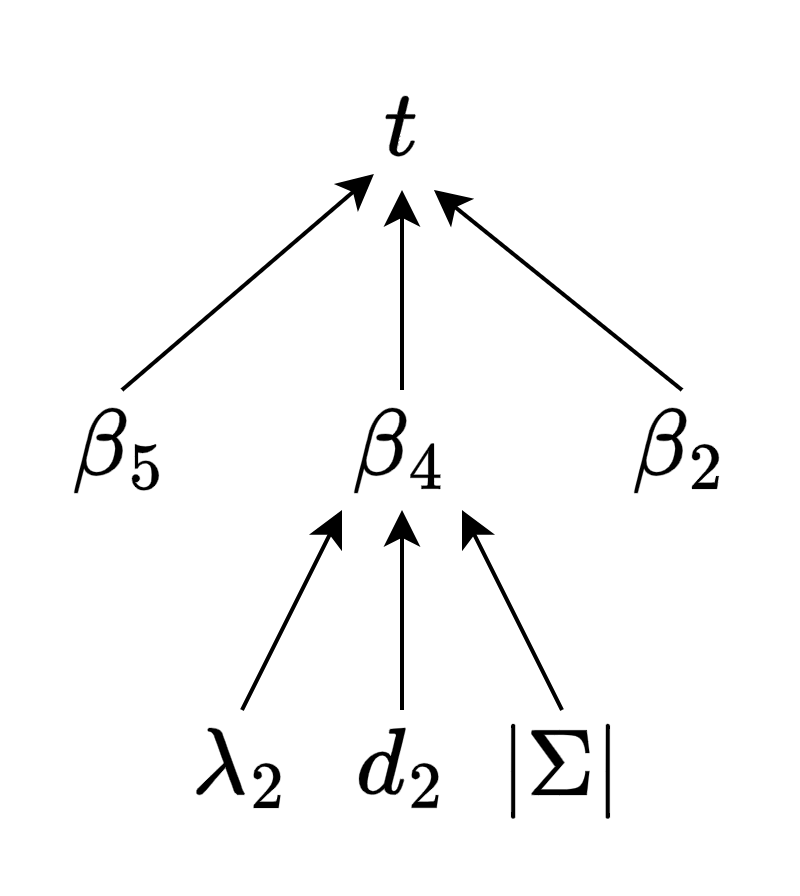パラメータの従属関係
ここで, $|\Sigma|$は与えられた制約グラフのアルファベットサイズであるものの, それ以外の$\beta_5,\lambda_2,\beta_2,d_2$は他の何にも依存しないuniversal constantです. サイズに関しても
\begin{align*} \mathrm{size}(G_5) &\le c_5 \cdot \mathrm{size}(G_4) \\ &\le c_5d_2^t \cdot \mathrm{size}(G_2) \\ &\le c_2c_5d_2^t \cdot \mathrm{size}(G) \end{align*}
となり, $c_2,c_5$はuniversal constantであり, $t$は$|\Sigma|$にのみ依存する.