森田『代数概論』第Ⅱ章 例4.2を理解しよう① 内部自己同型と部分群の共役
今回は群論についてのお話です。初学者向けの内容ですが、群の定義や部分群、準同型といったごく初歩的な概念、素数位数の群は巡回群であるなどの初歩的な事実については知っているものとします。
森田『代数概論』の第Ⅱ章 例4.2
群論において、以下の事実があります。
$p,q$ を素数とし、$p>q$, $q \nmid (p-1)$とする。このとき位数$pq$の群はアーベル群である。
この事実について、『代数概論』(森田康夫 著) の第Ⅱ章 例4.2 に以下のような証明が載っています。が、私が初めてこれを読んだときは、全く理解できませんでした。
以下、$N_G(P)$で$P$の$G$における正規化群を表します(正規化群の定義は後ほど紹介します)。
$p,q$を$p>q$なる素数とし、$G$を位数$pq$の有限群とする。このときシローの定理より、$G$はシロー$p$-部分群$P$を含む。$G\supset N_G(P) \supset P$かつ$[G:P]=q$は素数であるから、$N_G(P)=G$または$N_G(P)=P$となる。ところが、シローの定理より、$P$と共役な$G$の部分群の個数$[G:N_G(P)]$は$kp+1$の形であり、$1$でなければ$p$より大である。よって$[G:N_G(P)]=1$だから、$N_G(P)=G$となり、$P$は$G$の正規部分群となる。
$G$のシロー$q$-部分群を$Q$とする。$P \triangleleft G$より$PQ$は$G$の部分群となり、位数が$pq$の倍数だから、$PQ=G$となる。また位数の関係より$P \cap Q = \{1\}$となるから、$G$は$P$の$Q$による半直積となる。
$P \triangleleft G$だから、$Q$は$P$に内部自己同型写像で作用している。ところが$P \simeq \mathbb Z/p \mathbb Z$であるから、$\mathrm{Aut}(P)$は位数$p-1$の群である。したがって、$q$が$p-1$を割り切らないなら、$\mathrm{Aut}(P)$の部分群で$Q$の準同型像となり得るのは$\{1\}$のみである。したがって、$q\nmid (p-1)$なら$Q$は$P$の上に自明に($\mathrm{id}_P$として)作用し、$P$の元と$Q$の元は可換となる。よって、$q \nmid (p-1)$なら$G=PQ$は位数$pq$のアーベル群となる。
初見では、最初の方にいきなり$N_G(P)$が出てきた時点で「もう分からん」となりました(早)。$N_G(P)$の定義は字面だけは知っていましたが、この文脈との繋がりが分かりませんでした。他にも、この証明には慣れていないと読み取りにくい箇所がけっこうあると思います(私だけじゃないですよね……?)。
だいぶ後になって、この証明を理解することができました。その上、この証明がわりと自然な発想で得られるものだということが分かりました。というわけで、このシリーズでは上の証明を理解し、またいかに「自然」なのかを学んでいきたいと思います。
余談ですが、先日 OMC Proxima Technology杯 の予選に参加しました。そこで群論の問題が出たのですが、参加者の皆様の感想を眺めていると、部分群の個数を求める問題が解けなかった、という声がちらほらありました。私はなんとか解いたのですが、なぜ解けたのかを考えたところ、上の例を理解した経験があったのが1つの要因だったのかなと思いました。これがこの記事を書こうと思ったきっかけです。
シリーズは全4回の予定です。
第1回(今回)は第一段落を読むための準備で、第2回で第一段落を、第3回で第二段落を、第4回で第三段落を解説します。
内部自己同型
まずは基本的な概念から見ていきましょう。
$G$を群とし、$a \in G$を任意の元とする。このとき写像$I_a : G \to G$を
$$ I_a(x)=axa^{-1}$$
で定め、これを$a$の定める内部自己同型という。
内部自己同型は、その名の通り同型写像です。
$G$を群、$a \in G$を任意の元とする。任意の$x,y\in G$に対し、
$$ I_a(x)I_a(y)= axa^{-1} aya^{-1} = axya^{-1} = I_a(xy)$$
より、$I_a$は準同型。
また、$a^{-1}$の定める内部自己同型$I_{a^{-1}}$は$I_a$の逆写像となる。実際、任意の$x \in G$に対し
$$ I_a(I_{a^{-1}}(x)) = I_a(a^{-1}xa)=aa^{-1}xaa^{-1}=x,$$
$$ I_{a^{-1}}(I_a(x)) = I_{a^{-1}}(axa^{-1})=a^{-1}axa^{-1}a=x$$
となる。よって、$I_a$は同型写像である。
内部自己同型は「見方を変える」ようなイメージです。
例えば$4$次対称群$S_4$において、$I_{(34)}((123))$を計算してみます。$(34)^{-1}=(34)$なので、
$$ I_{(34)}((123)) = (34)(123)(34) = (124)$$
となり、ちょうど$3$と$4$のラベルを付け替える操作になっていることが見て取れます。一般に、$n$次対称群$S_n$における内部自己同型はラベルの付け替えになることが知られています。
あと、行列の対角化も似たような話ですね。
部分群の共役
内部自己同型で部分群を移すことを考えます。$G$を群、$H$を$G$の部分群、$a \in G$を任意の元とすると、
$$ I_a(H) = aHa^{-1}$$
です。$I_a$は同型写像だったので、$aHa^{-1}$も部分群で、しかも$H$と同型です。
群$G$の部分群$H_1,H_2$が共役であるとは、ある$a\in G$が存在して
$$ H_2 = aH_1a^{-1}$$
が成り立つことを言う。
上で見た通り、2つの部分群が共役ならば同型です。しかし、同型であっても共役とは限りません。
4次対称群$S_4$において、部分群$H_1=\{ \mathrm{id},(12) \}$と$H_2=\{ \mathrm{id},(12)(34) \}$は同型だが、ラベルの付け替えで移り合わないので、共役ではない。
よって、共役は同型よりも強い条件となっています。
正規部分群について
ここで、正規部分群について復習します。
群$G$の部分群$N$が正規部分群であるとは、任意の$a\in G$に対し
$$ N=aNa^{-1}$$
が成り立つことを言う。
言い換えれば、$N$が正規部分群であるとは、$N$と共役な部分群が$N$自身しかないということですね。
群$G$の部分群$N$について、
$$\begin{aligned}
N \text{ が } G \text{ の正規部分群} &\Longleftrightarrow \text{任意の } a \in G \text{ に対して } N=aNa^{-1}\\
&\Longleftrightarrow N \text{ と共役な } G \text{ の部分群が } N \text{ 自身しかない }
\end{aligned}$$
実はこの命題、結構重要です。
有限群の構造を調べる際、正規部分群が見つかれば大きな手がかりになります。そして、正規部分群を見つけるためによく使われる手法の1つが「ある部分群$H$と共役な部分群を数えてみたら1つしかなかった。よって$H$は正規部分群である」というものなのです。
といっても、共役な部分群の個数なんてどうやって数えれば良いのでしょうか?その手助けをしてくれるのが、以下で述べる正規化群と、次回扱うシローの定理です。
共役な部分群の個数
$G$を有限群とし、$H$をその部分群とします。$H$と共役な部分群について考えるため、次のような写像を考えます。
$$ \begin{matrix}
G & \to & \{H \text{ と共役な部分群}\}\\
a & \mapsto & aHa^{-1}
\end{matrix}$$
なお、$\{H \text{ と共役な部分群}\}$という集合には演算が入っていないので、この写像は(群準同型などではなく)単なる集合としての写像です。
つまりこれはある種の「群作用」を考えているわけですが、ここではできるだけ予備知識を少なくしたいため、群作用に関する用語は明示的には使わずに進めたいと思います。
どの部分群に移るかによって、$G$を分割することができます。
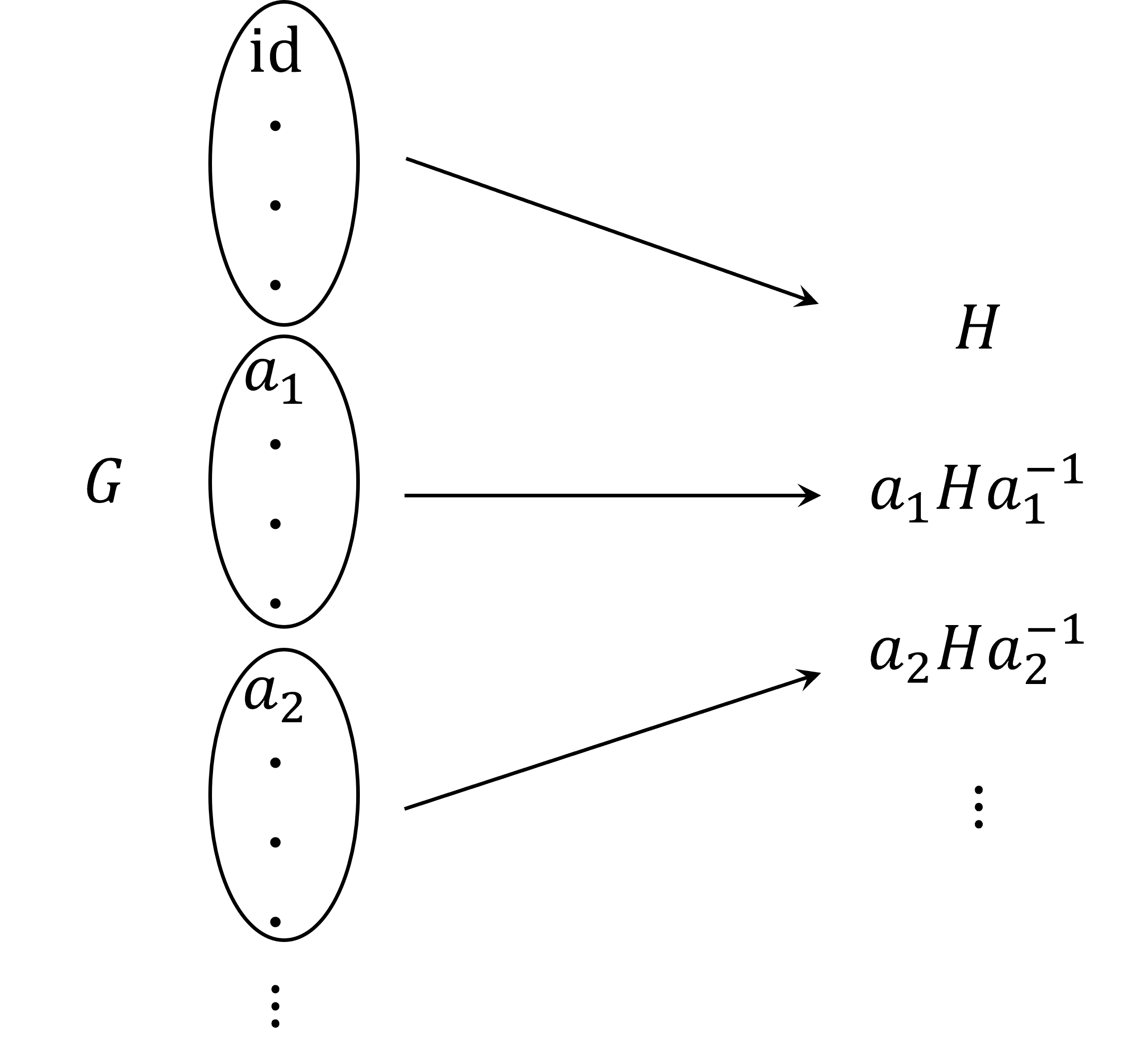
記号を使うとごちゃごちゃしちゃいそうなので、図でごり押そうと思います。
ここで、重要な事実があります。それは、上のように分割されたそれぞれの集合は、すべて要素の個数が等しいということです。以下、このことについて見ていきます。
正規化群
まず、$H$を動かさない、すなわち$aHa^{-1}=H$を満たす$a$に着目します。
群$G$とその部分群$H$に対し
$$ N_G(H) = \{ a \in G \ | \ aHa^{-1} = H \}$$
と定め、これを$H$の$G$における正規化群という。
基本的な性質を見ていきます。
$N_G(H)$は$G$の部分群である。
$a,b \in N_G(H)$とすると、
$$ abH(ab)^{-1} = a(bHb^{-1})a^{-1} = aHa^{-1} = H$$
$$ 1 H 1^{-1} = H$$
$$ a^{-1}Ha = a^{-1}(aHa^{-1})a = H$$
より$ab, 1,a^{-1} \in N_G(H)$である。よって、$N_g(H)$は$G$の部分群である。
$H \subset N_G(H)$が成り立つ。
任意の$h \in H$ に対し、$hHh^{-1} = H$であるから$h \in N_G(H)$.
あらためて図を書くと、こんな感じです。
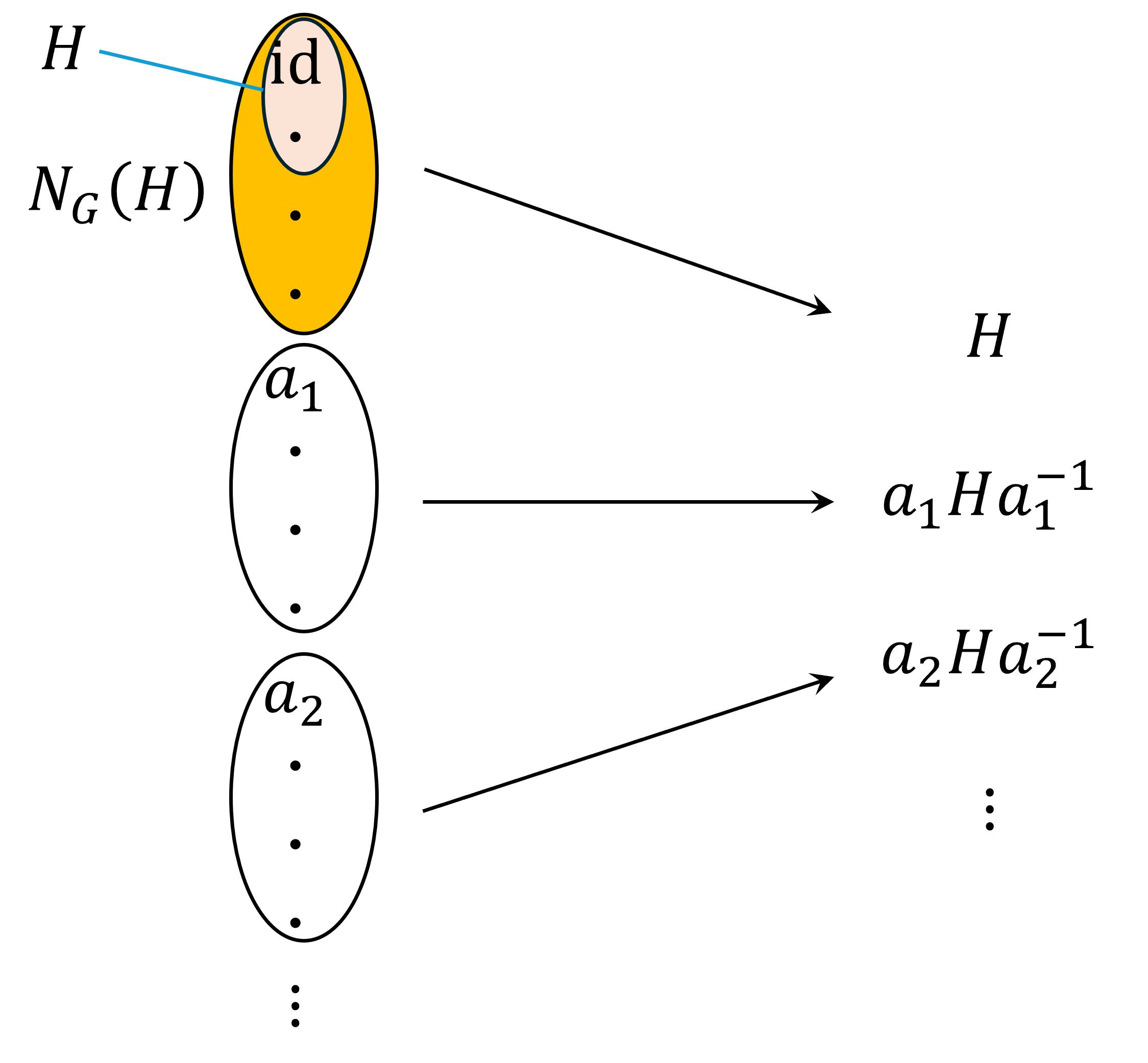
「正規化群」という名前については、$H$が$N_G(H)$の正規部分群になること、また、そのような性質(すなわち、$H$を含む$G$の部分群$K$であって$H$が$K$の正規部分群になる)を持つ群の中で最大のものが$N_G(H)$であることから来ているのだと思います。
次に、ある$a \in G$を固定し、
$$ aHa^{-1} = bHb^{-1}$$
を満たす$b$について考えます。
$$ \begin{aligned}
aHa^{-1} = bHb^{-1} &\Longleftrightarrow H=a^{-1}bHb^{-1}a\\
&\Longleftrightarrow H=(a^{-1}b)H(a^{-1}b)^{-1}\\
&\Longleftrightarrow a^{-1}b \in N_G(H)\\
&\Longleftrightarrow b \in aN_G(H)
\end{aligned}$$
より、
$aHa^{-1} = bHb^{-1}$を満たす$b$全体の集合は、$aN_G(H)$に等しい。
となります。図で見ると、
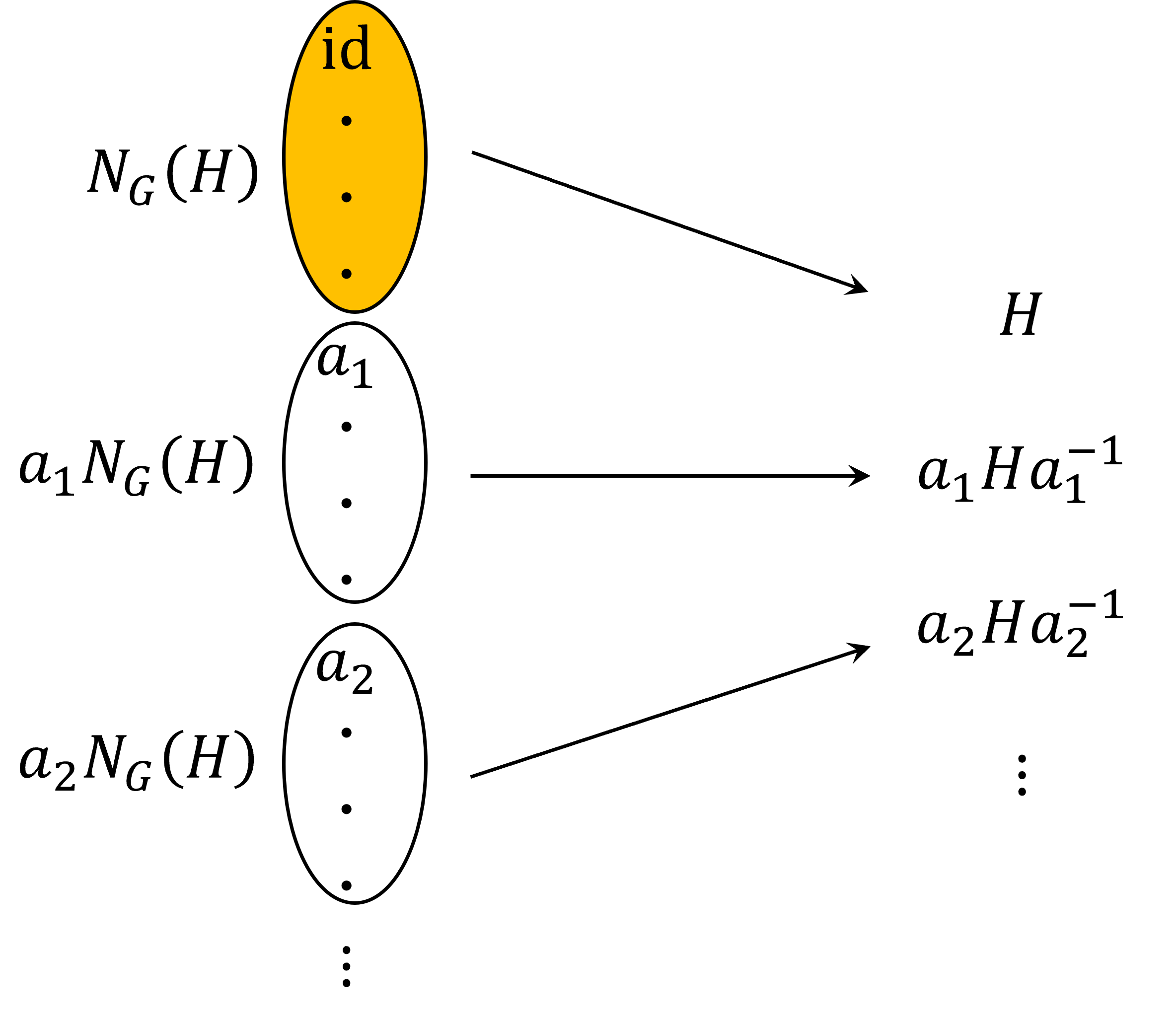
という感じです。
任意の$a\in G$に対して$|aN_G(H)| = |N_G(H)|$なので、分割されたそれぞれの集合はすべて要素の個数が等しいことが確かめられました。
これにより、次が得られます。
有限群$G$において、部分群$H$と共役な部分群の個数は$\disp \frac {|G|}{|N_G(H)|}$, すなわち指数$[G : N_G(H)]$に等しい。
これが、共役な部分群の個数を数える1つの手がかりとなります。
一般には$N_G(H)$の位数や指数を求めるのも簡単ではありませんが、すぐに分かることもあります。
先ほど見たように$H \subset N_G(H)$が成り立つので、$|N_G(H)|$は$|H|$の倍数です。したがって、
群$G$において、部分群$H$と共役な部分群の個数は指数$[G : H]$の約数である。
が従います。
今回はここまでとします。
次回はシローの定理について解説し、『代数概論』の例の第一段落を見ていきます。