文献あり

「Melid Geometry Contest - 2nd」の公式解説

こんにちは．Melidです．
2025年12月23日から同月26日にかけて純粋幾何のコンテスト(Melid Geometry Contest - 2nd)を開催させていただきました．
本記事ではその問題の公式解説を掲載します．

問題

以下，特に記載が無い限り，「$XY$」で「直線$XY$」，「円$XYZ$」で「三角形$XYZ$の外接円」を表す．

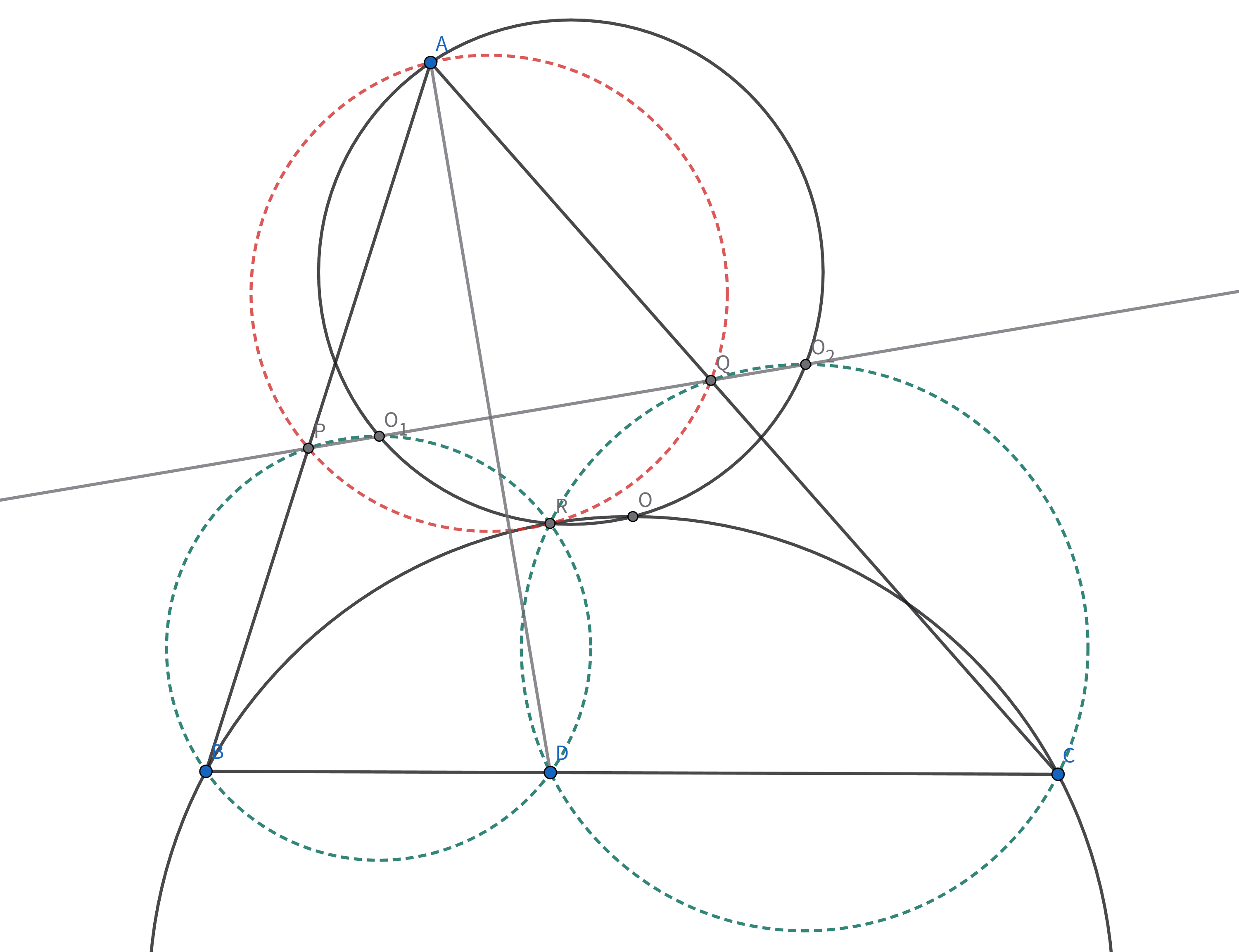
三角形$ABC$において，$D$を$BC$上の$B，C$と異なる点とし，三角形$ABC，ABD，ACD$の外心をそれぞれ$O，O_{1}，O_{2}$とする．$O_{1}O_{2}$と$AB，AC$の交点をそれぞれ$P，Q$とし，円$OO_{1}O_{2}$と円$OBC$の交点を$R(\ne O)$とするとき，$∠PRO_{1}=∠QRO_{2}$を示せ．

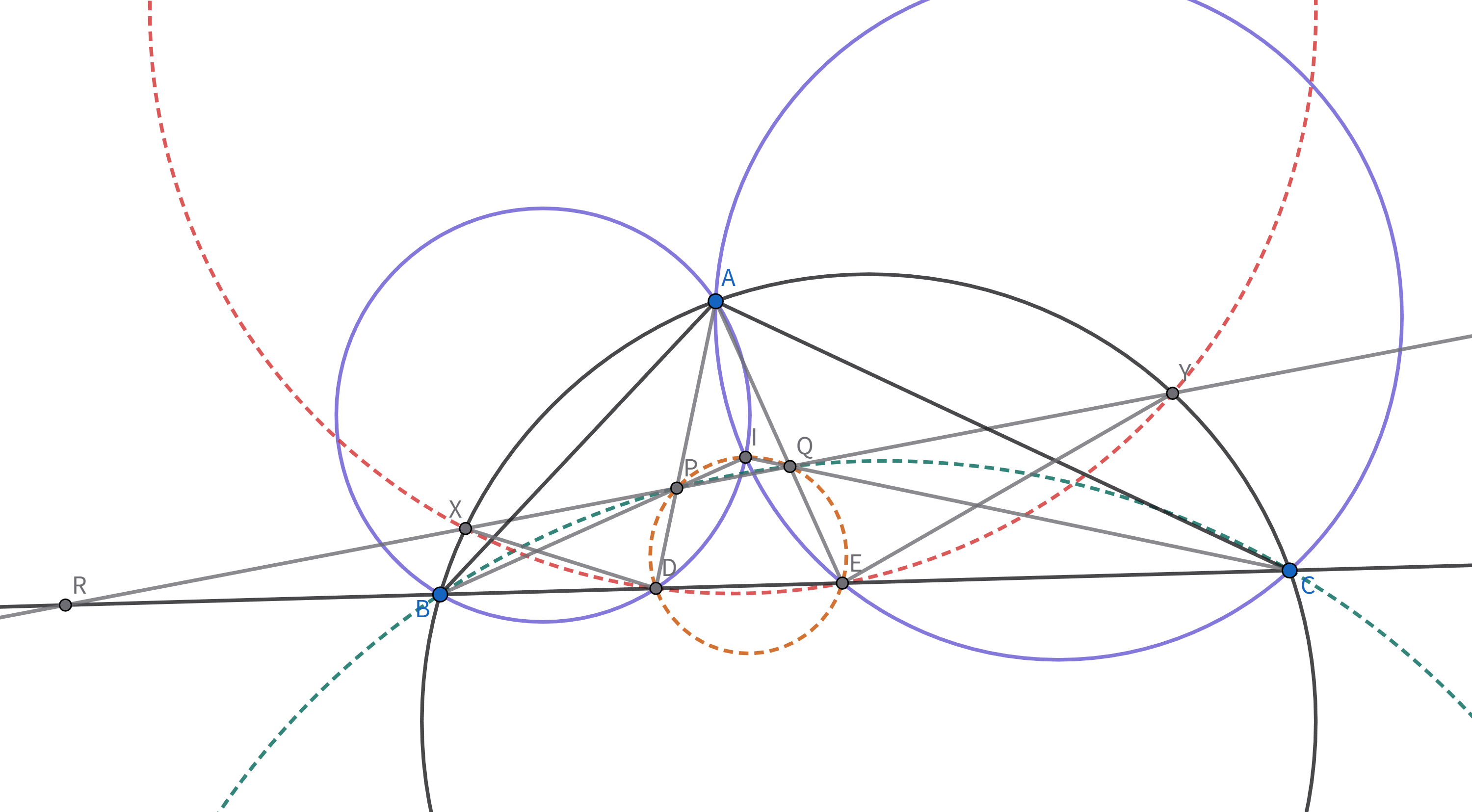
$∠A>90^{\circ}$を満たす不等辺三角形$ABC$において，その内心を$I$とし，円$ABI，ACI$と$BC$の交点をそれぞれ$D(\ne B)，E(\ne C)$とする．$AD$と$BI$の交点を$P$，$AE$と$CI$の交点を$Q$とし，$PQ$と円$ABC$の2つの交点を$X，Y$とする．このとき，$∠XDA=∠YEA$を示せ．

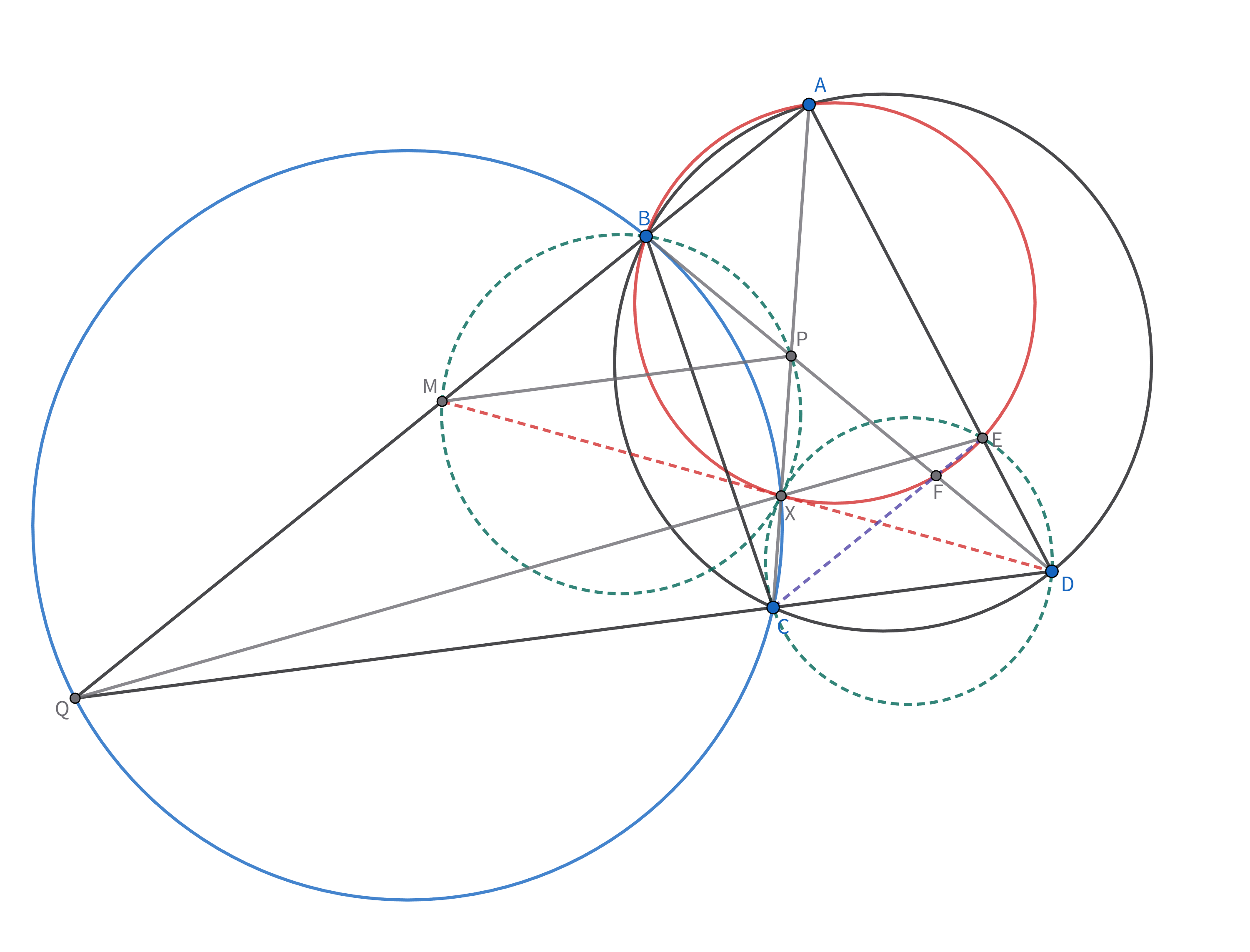
円に内接する四角形$ABCD$において，$AC$と$BD$の交点を$P$，$AB$と$CD$の交点を$Q$とする．円$QBC$と$AC$の交点を$X(\ne C)$とし，線分$AQ$の中点を$M$とする．$AD=BD，PA=PC$であるとき，$DM$と円$ABX$は接することを示せ．

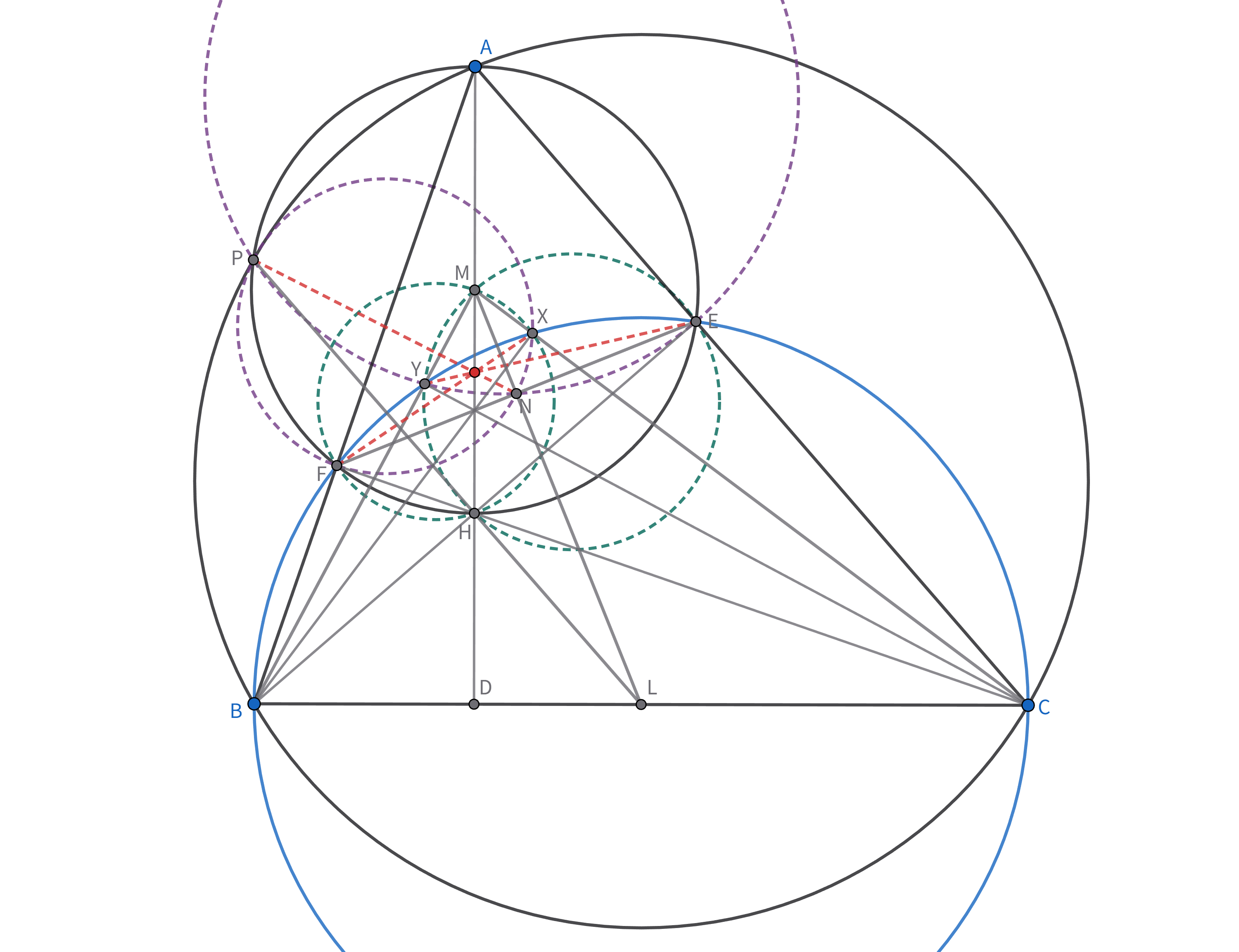
直角三角形でない不等辺三角形$ABC$において，$B，C$から$AC，AB$に下ろした垂線の足をそれぞれ$E，F$とし，円$AEF$の中心を$M$，円$ABC$と円$AEF$が再び交わる点を$P$とする．線分$EF$の中点を$N$とし，$B，C$から$MC，MB$に下ろした垂線の足をそれぞれ$X，Y$とするとき，$AM，EY，FX，PN$は一点で交わることを示せ．

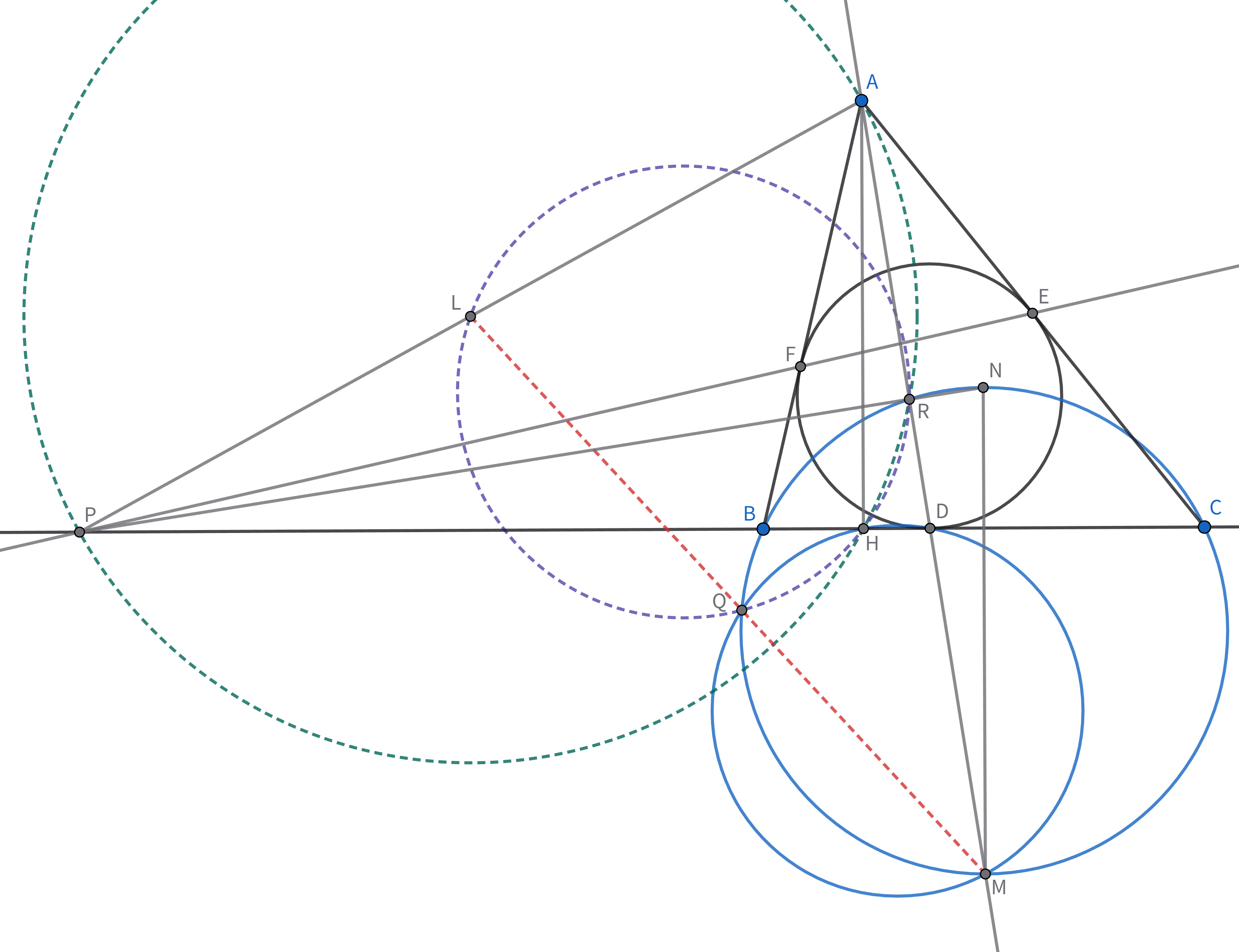
直角三角形でない不等辺三角形$ABC$において，その内接円と$BC，CA，AB$の接点をそれぞれ$D，E，F$とし，$A$から$BC$に下ろした垂線の足を$H$とする．$BC$と$EF$の交点を$P$とし，$AD$上に$BM=CM$を満たすように点$M$をとる．円$BCM$と円$DHM$の交点を$Q(\ne M)$とするとき，$MQ$は線分$AP$の中点を通ることを示せ．

難易度はJMO本戦1～3番級を想定しています．

解説

問題1

$\measuredangle ADB=\measuredangle ADC$より$\measuredangle AO_{1}B=\measuredangle AO_{2}C$であるため，$\triangle AO_{1}B\sim\triangle AO_{2}C$である．回転相似を考えて，$\triangle ABC\sim\triangle AO_{1}O_{2}$であるから，$\measuredangle O_{1}AO_{2}=\measuredangle BAC$．また，$OO_{1}\perp AB，OO_{2}\perp AC$より，$\measuredangle O_{1}OO_{2}=\measuredangle BAC$であるので，前の議論と併せて$A，O_{1}，O，O_{2}$は共円である．
$O_{1}O_{2}$は$AD$の垂直二等分線であるため，$\measuredangle O_{1}PA=90^{\circ}-\measuredangle PAD=\measuredangle BDO_{1}$より，$O_{1}，P，B，D$は共円．さらに，$2\measuredangle ABC=\measuredangle AO_{1}D=\measuredangle AOC$であるから，$\triangle AO_{1}D\sim\triangle AOC$．回転相似を考えて，$\triangle AO_{1}O\sim\triangle ADC$であるから，$\measuredangle O_{1}RB=\measuredangle O_{1}RO+\measuredangle ORB=\measuredangle O_{1}AO+\measuredangle OCB=\measuredangle DAC+(90^{\circ}-\measuredangle BAC)=90^{\circ}+\measuredangle DAB=\measuredangle O_{1}PB$より，$O_{1}，P，B，R$は共円．すなわち，$O_{1}，P，B，D，R$は共円である．同様に$O_{2}，Q，C，D，R$も共円であり，Miquel点の性質から$A，P，R，Q$の共円も従う．
よって，$\measuredangle PRQ=\measuredangle PAQ=\measuredangle O_{1}AO_{2}=\measuredangle O_{1}RO_{2}$より示された．$\square$

問題2

$PQ$と$BC$の交点を$R$とする．$I$は弧$AID$及び弧$AIE$の中点であるため，shooting lemmaより$IP\times IB=IA^{2}=IQ\times IC$となり，$P，B，C，Q$の共円が従う．また，$\angle IQP=\angle IBC=\angle IDP$より，$I，P，D，Q$は共円．同様にして$I，P，E，Q$の共円を得られるため，$I，P，D，E，Q$は共円である．よって，$RX\times RY=RB\times RC=RP\times RQ=RD\times RE$より$X，D，E，Y$も共円である．従って，$\measuredangle XDA=\measuredangle BDA-\measuredangle BDX=\measuredangle EQP-\measuredangle EYX=\measuredangle AEY$より示された．$\square$

問題3

$AD$と$QX$の交点を$E$とし，円$ABX$と$BD$の交点を$F(\ne B)$とする．$\angle BAE=\angle BCQ=\angle BXQ$より，$A，B，X，F，E$は共円である．shooting lemmaより$BD$と円$BQC$は接するため，$BP\times PF=AP\times PX=PC\times PX=BP^{2}$より，$BP=PF$である．すなわち，四角形$ABCF$は平行四辺形であり，これと四角形$ABFE$が等脚台形であることを併せて，$C，F，E$の共線が従う．また，$\angle AMP=\angle AQC=\angle BXP$より，$B，M，X，P$は共円である．さらに，Miquel点の性質より$X，C，D，E$も共円であるので，$\angle MXP=\angle ABP=\angle DAB=\angle DEC=\angle DXC$より，$M，X，D$は共線である．よって，$\angle BXM=\angle BPM=\angle BDC=\angle BAX$より示された．$\square$

問題4

$A$から$BC$に下ろした垂線の足を$D$，線分$BC$の中点を$L$とし，$\triangle ABC$の垂心を$H$とする．$B，F，Y，X，E，C$は共円である．$E，H，D，C$及び$M，Y，D，C$はそれぞれ共円なので，$BY\times BM=BD\times BC=BH\times BE$より，$M，Y，H，E$は共円である．同様に，$M，X，H，F$は共円であるので，円$MYHE，MXHF，XYFE$に根軸定理を適用して，$MH，FX，EY$は共点である．
また，Newton–Gauss線を考えて，$M，N，L$は共線である．有名事実から$P，H，L$は共線であり，$LE，LF$は円$AEF$と接する．従って，円$XYFE$で円$MYHE，MXHF$を反転して，$N，Y，P，E$及び$N，X，P，F$は共円であることが得られる．円$NYPE，NXPF，XYFE$に根軸定理を適用して，$PN，FX，EY$は共点であるので，前の議論と併せて示された．$\square$

問題5

線分$AP$の中点を$L$，円$BCM$における$M$の対蹠点を$N$とし，$AM$と円$BCM$の交点を$R(\ne M)$とする．$AD，BE，CF$は一点($\triangle ABC$のGergonne点)で交わるため，$(B,C;D,P)=-1$である．$RD$は$\angle BRC$を二等分するので，Apollonius円を考えて，$\angle PRD=90^{\circ}$である．すなわち，$A，P，H，R$は$AP$を直径とする円上にある．$\measuredangle RQH=\measuredangle RQM-\measuredangle HQM=\measuredangle RNM-\measuredangle HDR=2\measuredangle RDH=2\measuredangle RAH=\measuredangle RLH$より，$L，Q，H，R$は共円である．従って，$\measuredangle LQR=\measuredangle LHR=90^{\circ}-\measuredangle RAH=\measuredangle HDR=\measuredangle MNR=\measuredangle MQR$より示された．$\square$