大学数学基礎解説

【構造力学】断面二次モーメントについての話

積分

構造力学の授業で，断面二次モーメントに関する定理が出てきました．その証明をします．

まずは定義

断面二次モーメント

$I_{x} = \int y^{2} d A$

ここで， $d A = B d y$ で， $B$ は $x$ 軸方向に平行な幅です．
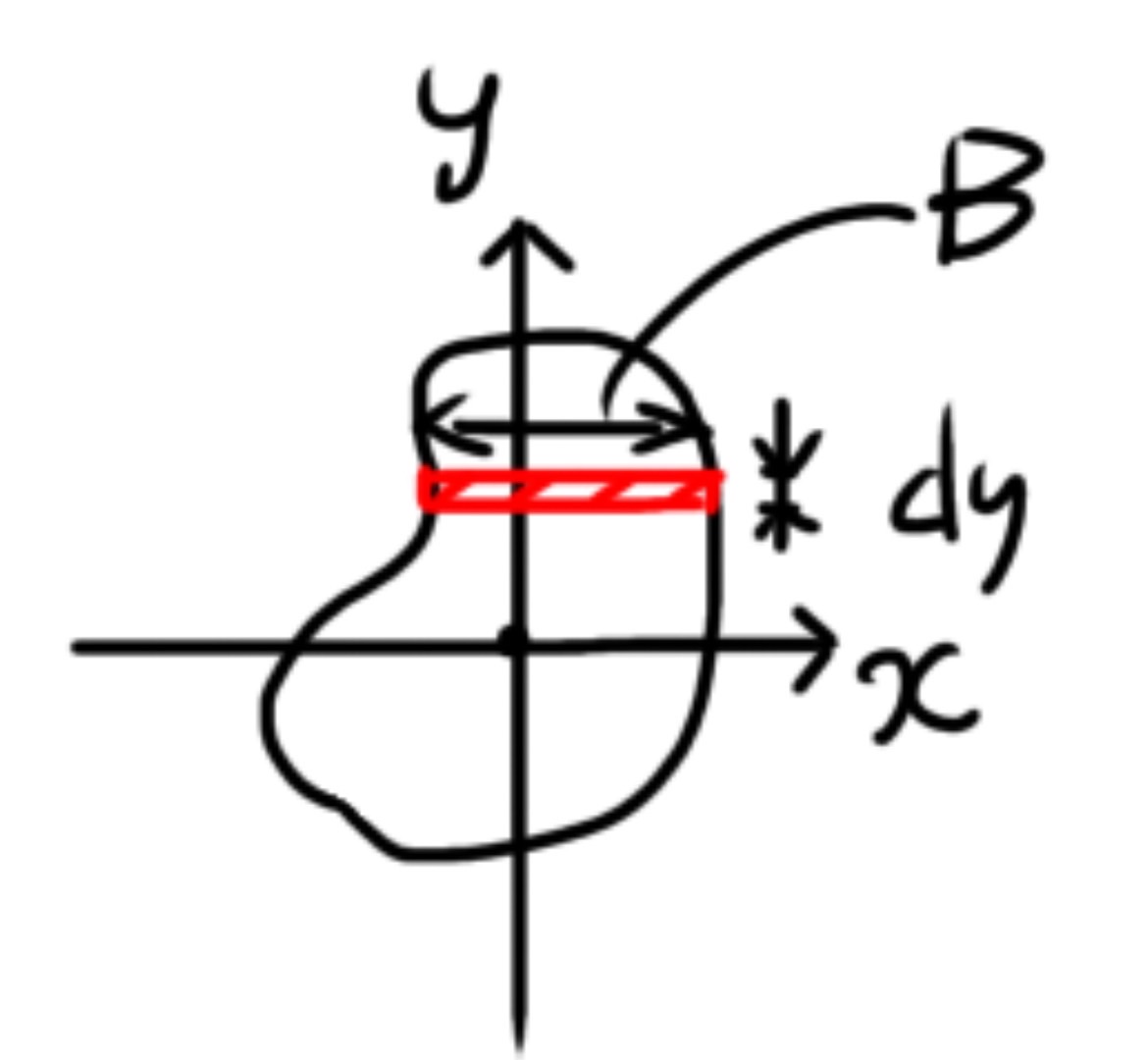微小断面

断面二次モーメントの和についての定理

$I_{x} + I_{y} = I_{X} + I_{Y}$
重心を通り直行する2軸における断面二次モーメントの和は，その軸の取り方に依らず一定である．

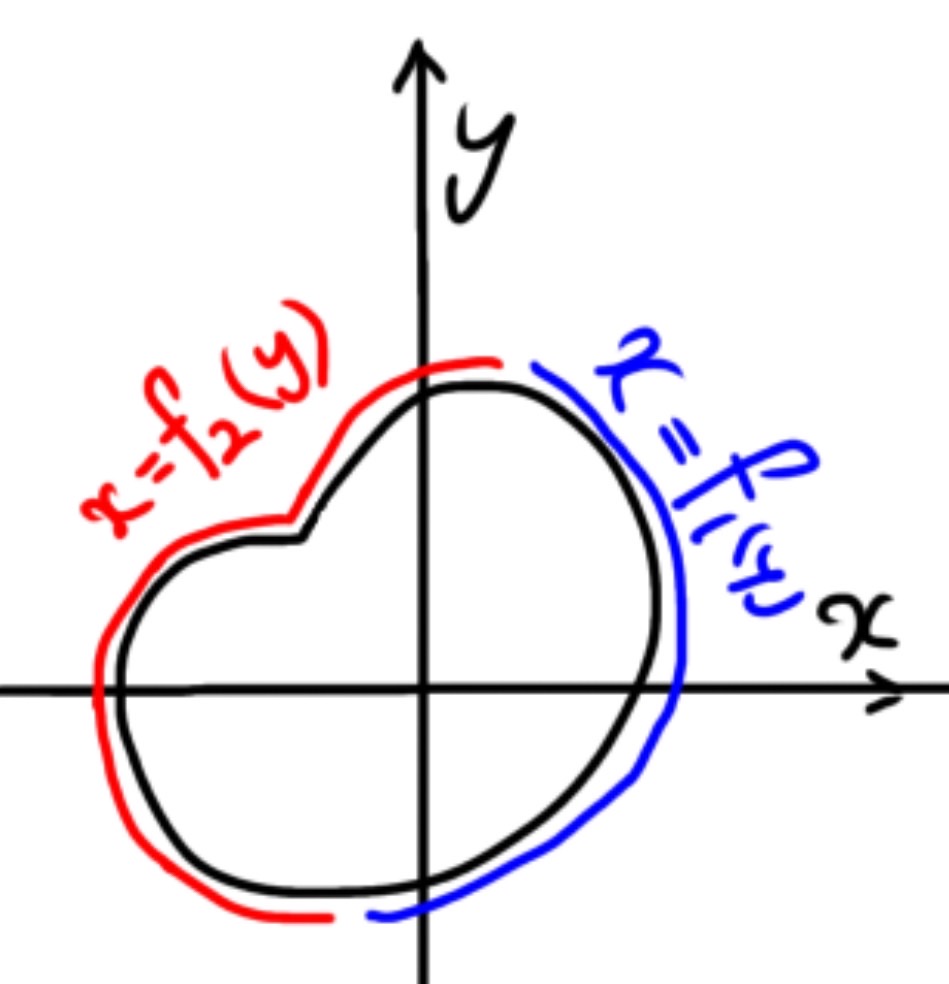f_1とf_2の説明
$\begin{array}{rcl} I_{x} & = & \int y^{2} d A \\ = & \int_{a}^{b} y^{2} (f_{1} (y) - f_{2} (y)) d y \\ = & \int_{a}^{b} y^{2} \int_{f_{2} (y)}^{f_{1} (y)} d x d y \\ = & \iint_{D} y^{2} d D \end{array}$
故に，
$\begin{array}{rcl} I_{x} + I_{y} & = & \iint_{D} (x^{2} + y^{2}) d D \\ = & \int_{0}^{2 π} \int_{0}^{r (θ)} r^{3} d r d θ (x \mapsto r \cos θ, y \mapsto r \sin θ) \\ = & \int_{0}^{2 π} \frac{1}{4} (r (θ))^{4} d θ \end{array}$
$r (θ + 2 π) = r (θ)$ とし， $X Y$ 座標が $x y$ 座標に対し $α$ だけ傾いていて，
$\begin{array}{rcl} I_{x} + I_{y} - I_{X} - I_{Y} & = & \int_{0}^{2 π} \frac{1}{4} (r (θ))^{4} d θ - \int_{α}^{2 π + α} \frac{1}{4} (r (θ))^{4} d θ \\ = & \int_{0}^{α} \frac{1}{4} (r (θ))^{4} d θ - \int_{2 π}^{2 π + α} \frac{1}{4} (r (θ))^{4} d θ \\ = & 0 (第二項を 2 π + θ \mapsto θ と置換) \end{array}$

具体的な計算で確認してみましょう．

一辺

a

の正方形の断面二次モーメント

$I_{x} = I_{y} = I_{X} = I_{Y} = \frac{a^{4}}{12}$
$X Y$ 座標は45度傾けたものとします．

$\begin{array}{rcl} I_{x} & = & \int y^{2} d A \\ = & \int_{- \frac{a}{2}}^{\frac{a}{2}} y^{2} a d y \\ = & \frac{a^{4}}{12} \\ I_{X} & = & \int Y^{2} d A \\ = & 4 \int_{0}^{\frac{a}{\sqrt{2}}} Y^{2} (\frac{a}{\sqrt{2}} - Y) d Y \\ = & a^{4} B (3, 2) (Y \mapsto \frac{a}{\sqrt{2}} Y) \\ = & \frac{a^{4}}{12} \end{array}$
beta関数を使いました．