東大院試04-A5

問題

考察

$\lambda=0$なら，初等的な微分積分の議論で行けるのになぁ．．．
$$\int_{-\infty}^\infty\frac{e^x}{1+e^{3x}}dx=\int_0^\infty\frac{1}{1+t^3}dt$$
となり，あとは（かなり面倒ではあるが）頑張ればいける．このことから，この問題は（多分）かなり面倒くさそうであることが分かる．

解答

$$f(z)=e^{i\lambda z}\frac{e^z}{1+e^{3z}}=\frac{e^{(i\lambda+1)z}}{1+e^{3z}}$$
を考える．まずはこの関数の極を求める．
$$1+e^{3z}=0$$を解いて，$\displaystyle z=(\frac{1}{3}+2k)\pi i$（$k\in\mathbb{Z}$）が特異点の候補であることが分かる．分子が指数関数で，$0$にならないことを考えると，これらは次数$1$の極であることが分かる．
積分路として，

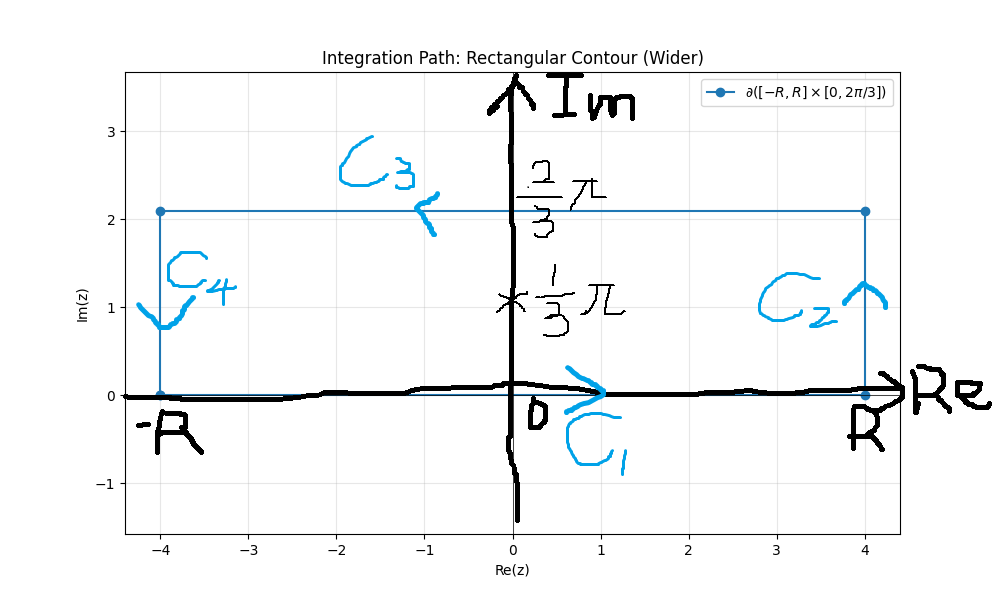
というものをとると，上手くいく．なぜ$\dfrac{2}{3}\pi i$を通るようにするかは後でわかる．
　$C_1$については，
$$\int_{C_1}f(z)dz=\int_{-R}^Rf(x)dx$$
　$C_2$については$z=R+it$（$t:0\rightarrow\dfrac{2}{3}\pi$）とパラメータ付けして，
$$\left|\int_{C_2}f(z)dz\right|=\left|\int_0^{\frac{2}{3}\pi}\frac{e^{(i\lambda +1)(R+it)}}{1+e^{3(R+it)}}dt\right|\leq\frac{2}{3}\pi e^{3\pi|\lambda|/2}\frac{e^R}{e^{3R}-1}\rightarrow0\,(R\rightarrow\infty)$$
とわかる．途中で$|a+b|\ge|a|-|b|$を使う．
　$C_4$については$z=-R+it$（$t:\dfrac{2}{3}\pi\rightarrow0$）とパラメータ付けして，
$$\left|\int_{C_4}f(z)dz\right|=\left|\int_0^{\frac{2}{3}\pi}\frac{e^{(i\lambda +1)(-R+it)}}{1+e^{3(-R+it)}}dt\right|\leq\frac{2}{3}\pi e^{3\pi|\lambda|/2}\frac{e^{-R}}{1-e^{-3R}}\rightarrow0\,(R\rightarrow\infty)$$
とわかる．
　$C_3$については，
$$\int_R^{-R}\frac{e^{(i\lambda+1)(x+2\pi i/3)}}{1+e^{3(x+2\pi i/3)}}dx=-e^{(2\pi i/3)(i\lambda+1)}\int_{-R}^R\frac{e^{(i\lambda+1)}}{1+e^{3x}}dx$$
となってくれる！（こうなってくれるので$\dfrac{2}{3}\pi$を通るように積分路を考えた．）
　さて，留数を求める．
$$\text{Res}\left(f(z),z=\dfrac{\pi}{3}i\right)=-e^{(\pi i/3)(i\lambda+1)}\frac{1}{3}$$
となるので，
$$ \int_{-\infty}^\infty\frac{e^{(i\lambda+1)}}{1+e^{3x}}dx=\frac{2\pi i e^{(\pi i/3)(i\lambda +1)}}{3(e^{(2\pi i/3)(i\lambda +1)}-1)}$$

　これの実部を求めればよい．分子を簡単にすると，
$$2\pi e^{-\lambda\pi/3}(-\sin\dfrac{\pi}{3}+i\cos\dfrac{\pi}{3}).$$
分母を簡単にすると，
$$3\{(e^{-(2\pi\lambda/3)}\cos\frac{2\pi}{3}-1)+ie^{-(2\pi\lambda/3)}\sin \frac{2\pi}{3}\}$$
よって，
$$\int_{-\infty}^\infty\cos(\lambda x)\frac{e^x}{1+e^{3x}}dx=\frac{4\pi(e^{-\pi\lambda}+e^{-\lambda\pi/3})}{\sqrt{3}\{(e^{-(2\pi\lambda/3)}+2)^2+3e^{-(4\pi\lambda/3)}\}}$$
となる．計算がエグイです．