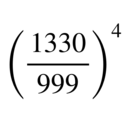二重指数(フェルマー数)が入った級数の和

問題

$$\sum_{n=0}^{\infty}\frac{2^n}{2^{2^n}+1}=\frac{1}{2+1}+\frac{2}{2^2+1}+\frac{4}{2^4+1}+\cdots=?$$

どーなるでしょーか？
この級数は分母がフェルマー数(二重指数)でめっちゃ収束が速いので、最初の数項を計算すれば収束値は予測できるのですが、ちゃんとその値に収束することを示せますか？

投稿日：2023年12月16日

更新日：2023年12月16日

この記事を高評価した人

高評価したユーザはいません

バッジはありません。

3506

数学科でもないしロクな大学受かったわけでもないしガッコーのお勉強なんかむしろサボりまくってるけれどちょっと面白い話がしたかっただけの一般人です。

コメントはありません。

読み込み中