T-DEMO Show 2025の3.の解法について
立見鶏と申します．今回も初等幾何の問題の自分なりの答案を残しておきます．「の」が多すぎて幸先が不安ですね．
T-DEMO Show 2025という初等幾何のコンテストがX上で開催されていました．
こちら
から確認できるはず．今回はこちらの第三問についてです．
と言っても．こちらのコンテスト（と言うよりは匿氏が主催のコンテスト）には模範解答がMathlog上に記事として残されております．本コンテストについても
こちら
に公式の解答がいくつかの別解つきで載せられております．すぐに読まずに，まずは自分の手で解いてみることをお勧めいたします．第一問は中学生の知識で十分で，良い演習問題となるはずです．
公式解説に主催者の解答，testerの別解，参加者の別解があるのに，いまさら何を……と思われるかもしれません．ごもっとも．少し経路の違う答案になりそうなので一応記事にしておこうか程度のものなのと，こんな大変なことをしなくても解ける想定解をちゃんと理解しようという反面教師的なものです．分量も計算も多い答案なので，流し読みを推奨．
まずは問題の紹介から．
問題3．
共軸な3円$\omega_0,\omega_1,\omega_2$があり，円$\omega_0$は円$\omega_1$を，円$\omega_1$は円$\omega_2$を，それぞれ内部に含みます．円$\omega_0$に内接する四角形$ABCD$において，2点$A,C$を結ぶ円弧$\gamma_1,\gamma_2,\gamma_3,\gamma_4$と，2点$B,D$を結ぶ円弧$\delta_1,\delta_2,\delta_3,\delta_4$が，各々この順に並んでいます．これら8本の円弧がすべて異なり，いずれも円$\omega_1$または円$\omega_2$に接するとき，以下の4円がすべて存在することを示してください．
円弧$\gamma_1,\gamma_2,\delta_1,\delta_2$のすべてに接する円．
円弧$\gamma_1,\gamma_2,\delta_3,\delta_4$のすべてに接する円．
円弧$\gamma_3,\gamma_4,\delta_1,\delta_2$のすべてに接する円．
円弧$\gamma_3,\gamma_4,\delta_3,\delta_4$のすべてに接する円．
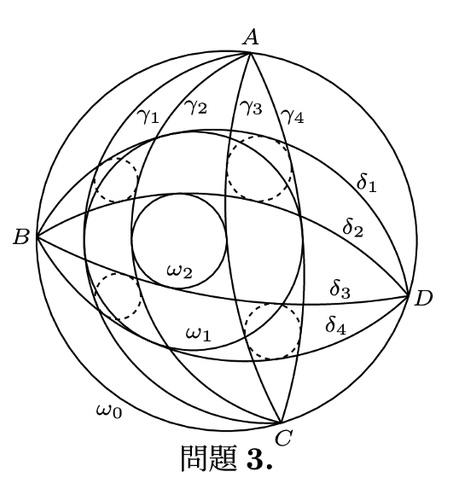本当に成り立つの……？？
問題の図中に直線が一切現れず，円弧と接するという条件だけで構成されている問題です．このままだと自由度が高すぎるので，まずは共軸について噛み砕いておきます．
包含関係にある双曲型円束は適当な反転によって同一中心円に移る
有識者の方々には明らかではあるが，念のため証明を．
共軸な3円$\omega_0,\omega_1,\omega_2$の中心を順に$O_0,O_1,O_2$とする．共軸よりある直線が存在しその直線上の点から3円への方べきが等しいことから，3点$O_0,O_1,O_2$は同一直線上でこの直線と垂直である．この直線と直線$O_0O_1$の交点を点$P$とし，点$P$から円$\omega_k$に引いた接線の接点を$A_k$とする．$PA_k$の長さは全て等しいので，$A_k$全てを通る円と直線$O_0O_1$の交点を下図のように点$Q,R$とする．
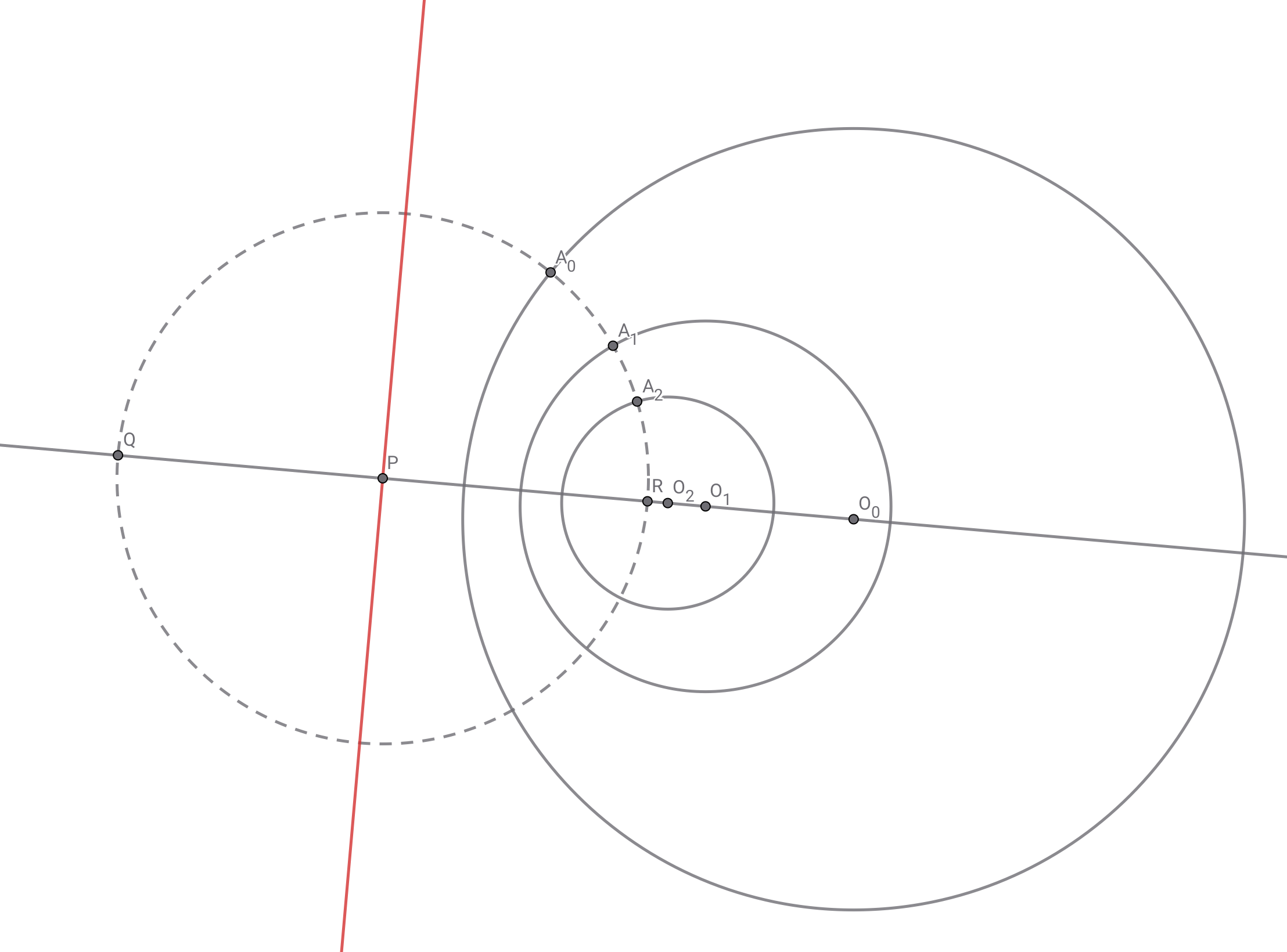
直線$QR$と円$\omega_0$の交点を$B_0,C_0$とする．（$Q,B_0,R,C_0$がこの順に並ぶように定める）
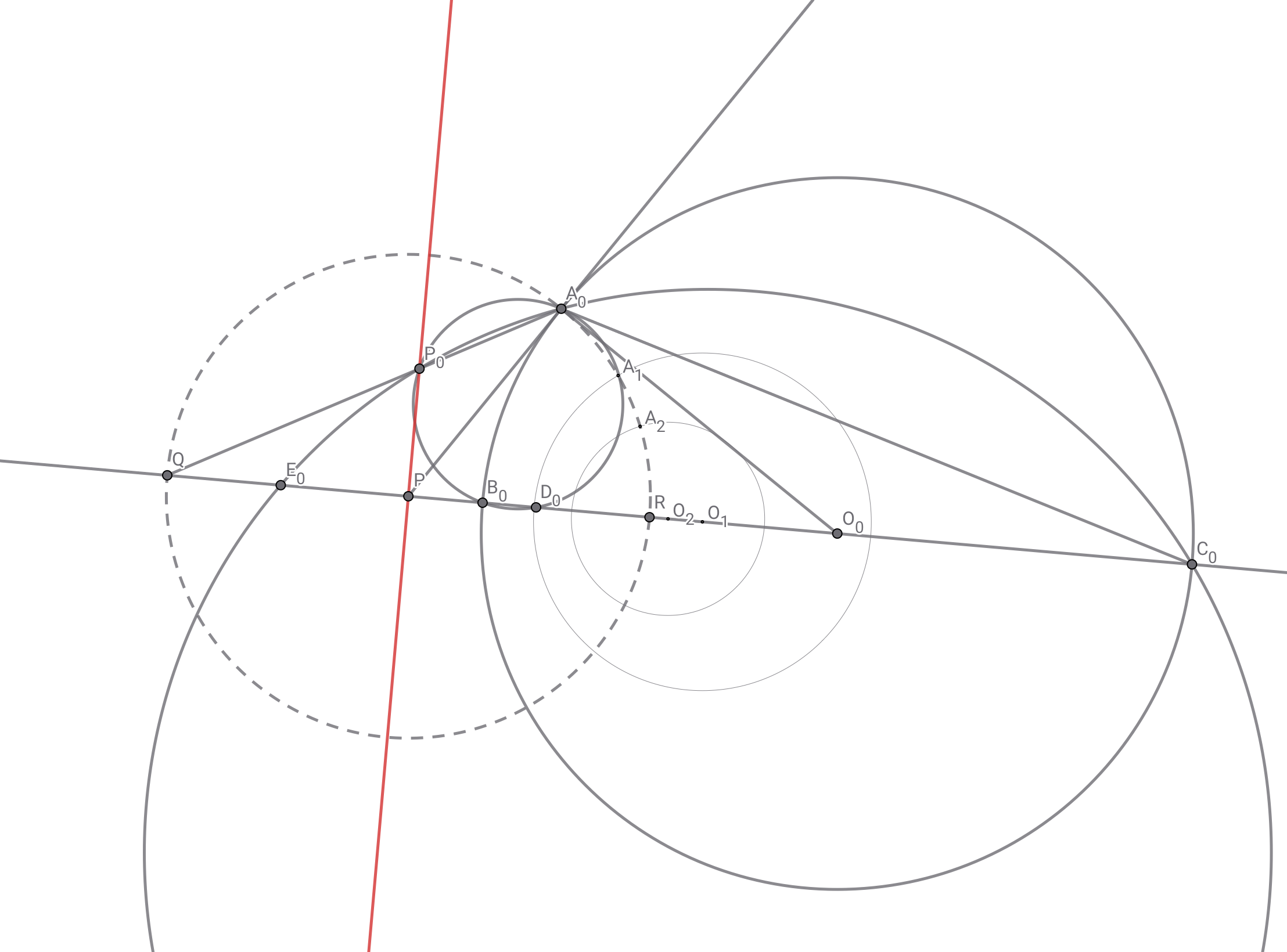
点$Q$を中心とする反転で点$P$が点$R$に移るものを考える．点$A_0$は直線$QA_0$と点$P$を通り直線$QR$に垂直な直線の交点と交わり，この点を$P_0$とする．またこの反転によって点$B_0,C_0$が移る点を$D_0,E_0$とする．
$\angle P_0D_0Q=\angle P_0A_0B_0=\angle P_0A_0P+\angle PA_0B_0=\angle A_0QP+\angle PC_0A_0$
$=\angle P_0E_0C_0$より$PD_0=PE_0$から円$\omega_0$をこの反転で移した円の中心は点$P$と一致する．これは円$\omega_1,\omega_2$でも同様である． ⬛︎
これを用いて元の問題を少し簡単にしましょう．なお公式解説と同様に，示すべき円は一つで十分なことにも留意しておきます．
問題3.改
点$O$を中心とする円$\omega_0,\omega_1,\omega_2$はこの順に大きいとします．円$\omega_0$に内接する四角形$ABCD$があり直線$AC$と$BD$の交点を$P$とします．円$\omega_1$上に点$E,G$を，円$\omega_2$上に点$F,H$を
$\cdot$3点$O,F,E$が同一直線上．
$\cdot$3点$O,H,G$が同一直線上．
$\cdot$三角形$ACE, BDG$の外接円が共に円$\omega_1$に接する．（この二円を順に$\gamma_1,\delta_1$とし，この二円の中心を順に$X_1,Y_1$としておく）
$\cdot$三角形$ACF, BDH$の外接円が共に円$\omega_2$に接する．（この二円を順に$\gamma_2,\delta_2$とし，この二円の中心を順に$X_2,Y_2$としておく）
を満たすようにとります．
このとき，三角形$ACE,ACF,BDG,BDH$の外接円全てと接する円が存在することを示してください．
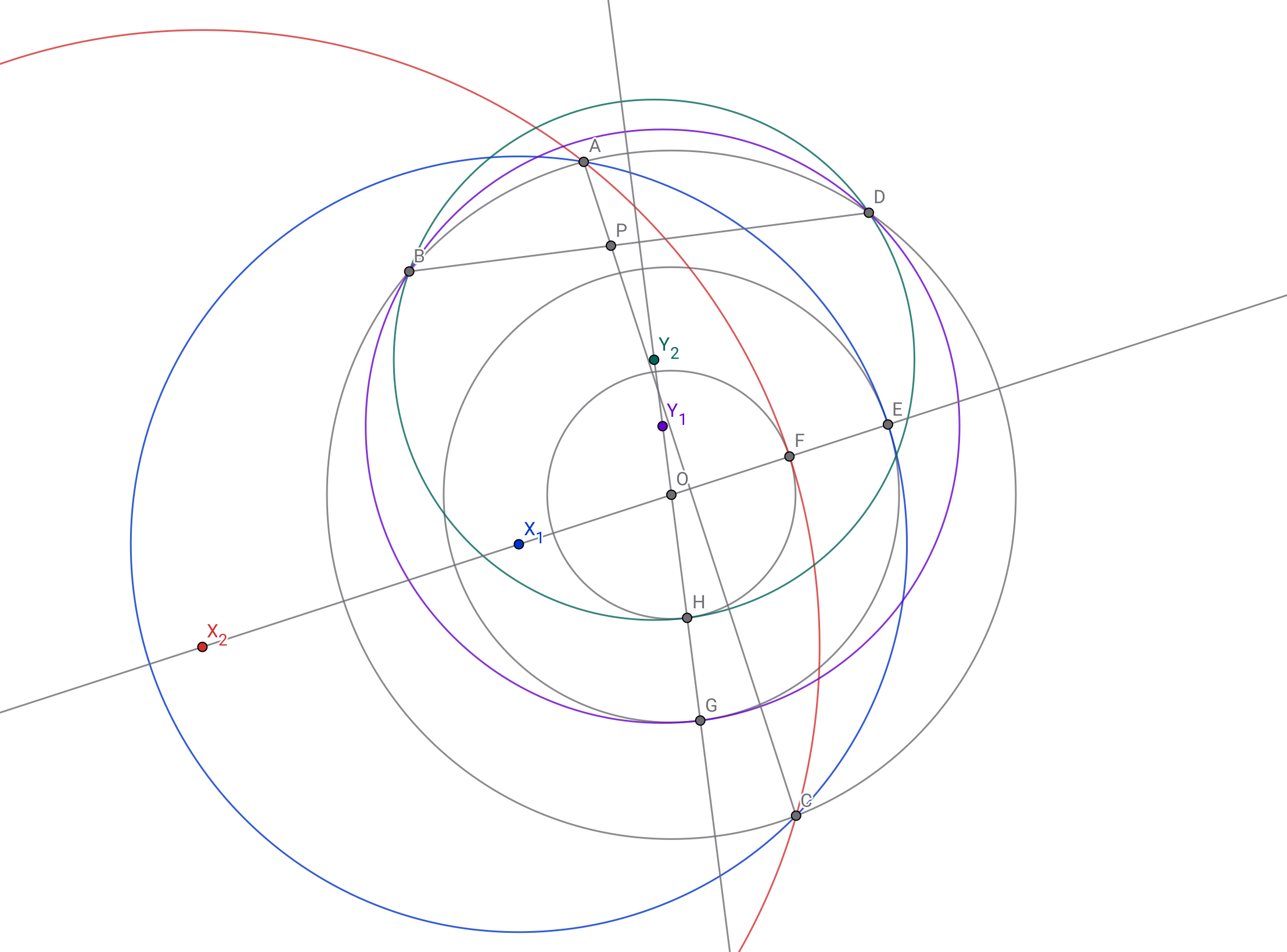少し簡単にしたとて……
ここでさらに補助点を6つ追加しておきましょう．2円に接する円を考える上で頻出の点なので自然に思い浮かぶと思われます．
円$\gamma_1,\gamma_2,\delta_1,\delta_2$の半径の長さを順に$r_1,r_2,s_1,s_2$とする．
$\cdot$線分$X_2Y_2$を$r_2:s_2$に外分する点を$I$
$\cdot$線分$X_1Y_1$を$r_1:s_1$に外分する点を$J$
$\cdot$線分$X_1X_2$を$r_1:r_2$に内分する点を$K$
$\cdot$線分$Y_1Y_2$を$s_1:s_2$に内分する点を$L$
$\cdot$線分$X_2Y_1$を$r_2:s_1$に内分する点を$M$
$\cdot$線分$X_1Y_2$を$r_1:s_2$に内分する点を$N$
とすると，6点$I,J,K,L,M,N$は同一直線上．
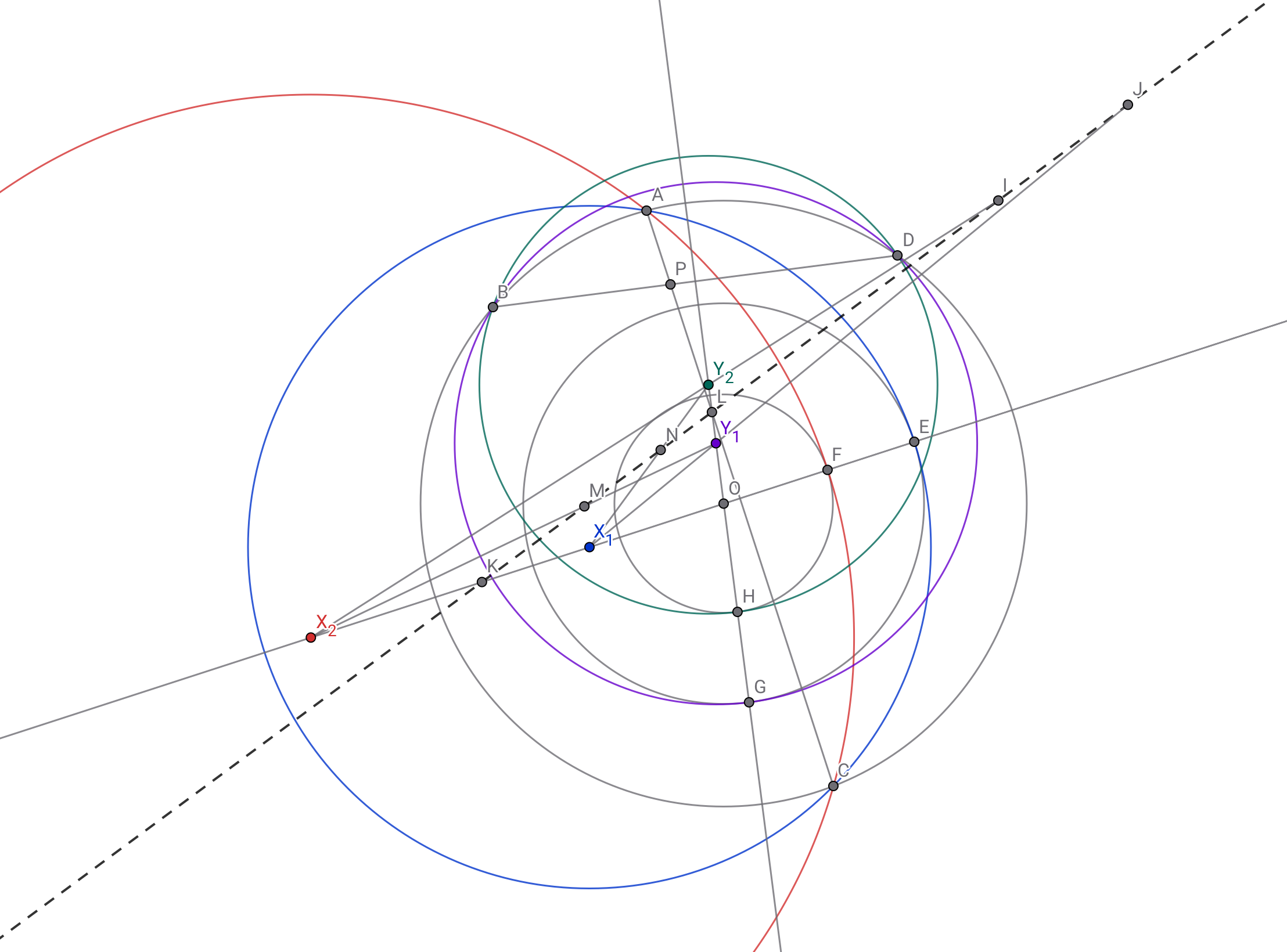転線の上に並ぶことを示したい
今回定義した点が重要であることは，例えば点$I$については円$\gamma_2$と$\delta_2$の両方に外接する円について，これらの円との接点を結ぶ直線が点$I$を通ることから雰囲気がわかるかと思われます．（というかこれが示されるのなら，そこから先は公式解説の方針と同様の考察で行けるのではと言う気も……）
$\dfrac{JY_1}{X_1J}\cdot\dfrac{MX_2}{Y_1M}\cdot\dfrac{KX_1}{X_2K}=\dfrac{s_1}{r_1}\cdot\dfrac{r_2}{s_1}\cdot\dfrac{r_1}{r_2}=1$
よりメネラウスの定理の逆から3点$J,M,K$は同一直線上．同様に3点$J,N,L$と$I,L,M$と$I,N,K$もそれぞれ同一直線上になる．
また$\dfrac{FO}{X_2F}\cdot\dfrac{HY_2}{OH}\cdot\dfrac{IX_2}{Y_2I}=1$より3点$I,F,H$は同一直線上にあり，同様に3点$J,E,G$も同一直線上にあることがわかる．
直線$AF$が円$\omega_0$と再び交わる点を$A'$とし，直線$OX_2$と点$A$を通り$AF$に垂直な直線，点$A'$を通り$AF$に垂直な直線の交点を順に$F_1,F_2$とする．
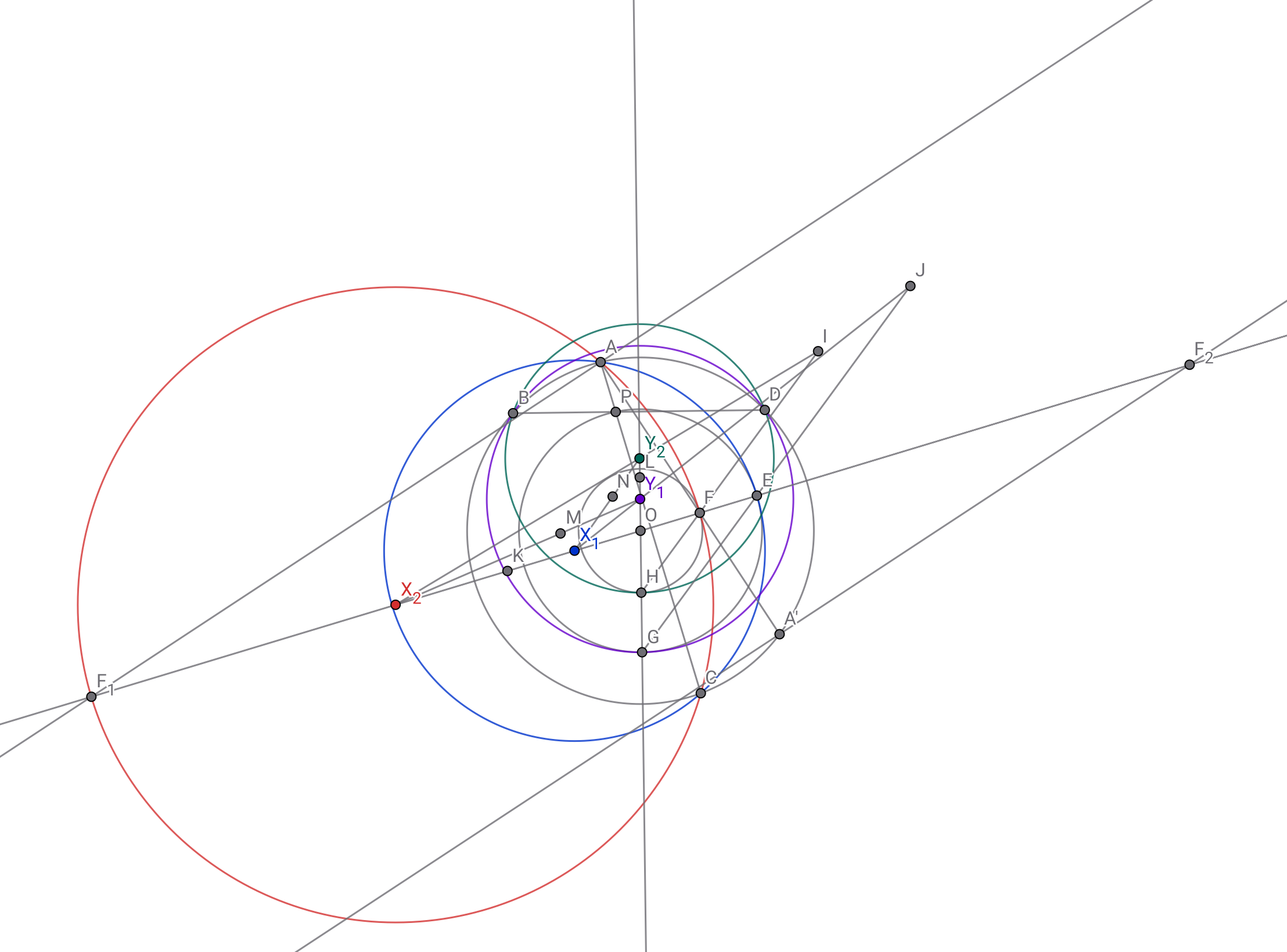急に外に広がる
$OA=OA'$より$OF_1=OF_2$となり，$FF_2=OF_2-OF=OF_1-OF=2OX_2$から$2OX_2=FF_2=FF_1\cdot\dfrac{A'F}{AF}=\dfrac{2FX_2}{AF^2}\cdot AF\cdot A'F$となり$OX_2=\dfrac{FX_2}{AF^2}\cdot (OA^2-OF^2)$が導かれる．同様の議論から$OY_2=\dfrac{HY_2}{BH^2}\cdot (OB^2-OH^2)$が言える．
ここでメネラウスの定理から$\dfrac{IF}{HI}\cdot\dfrac{X_2O}{FX_2}\cdot\dfrac{Y_2H}{OY_2}=1$であり，上記を代入して$\dfrac{IF}{HI}=\dfrac{AF^2}{BH^2}$がわかる．
また直線$AC$に関して点$E$と対称な点を$E'$とすれば，角度追跡及び相似から$FA^2=FK\cdot FE'$となり，直線$AC$に関して点$F$と対称な点を$F'$とすれば，$AF^2-AO^2=OF\cdot OF'=OF\cdot(EF'-OE)=OF\cdot(FE'-OE)$であり$OK=FK-OF=\dfrac{FA^2-FE'\cdot OF}{FE'}=\dfrac{AO^2-OE\cdot OF}{FE'}$が導かれる．
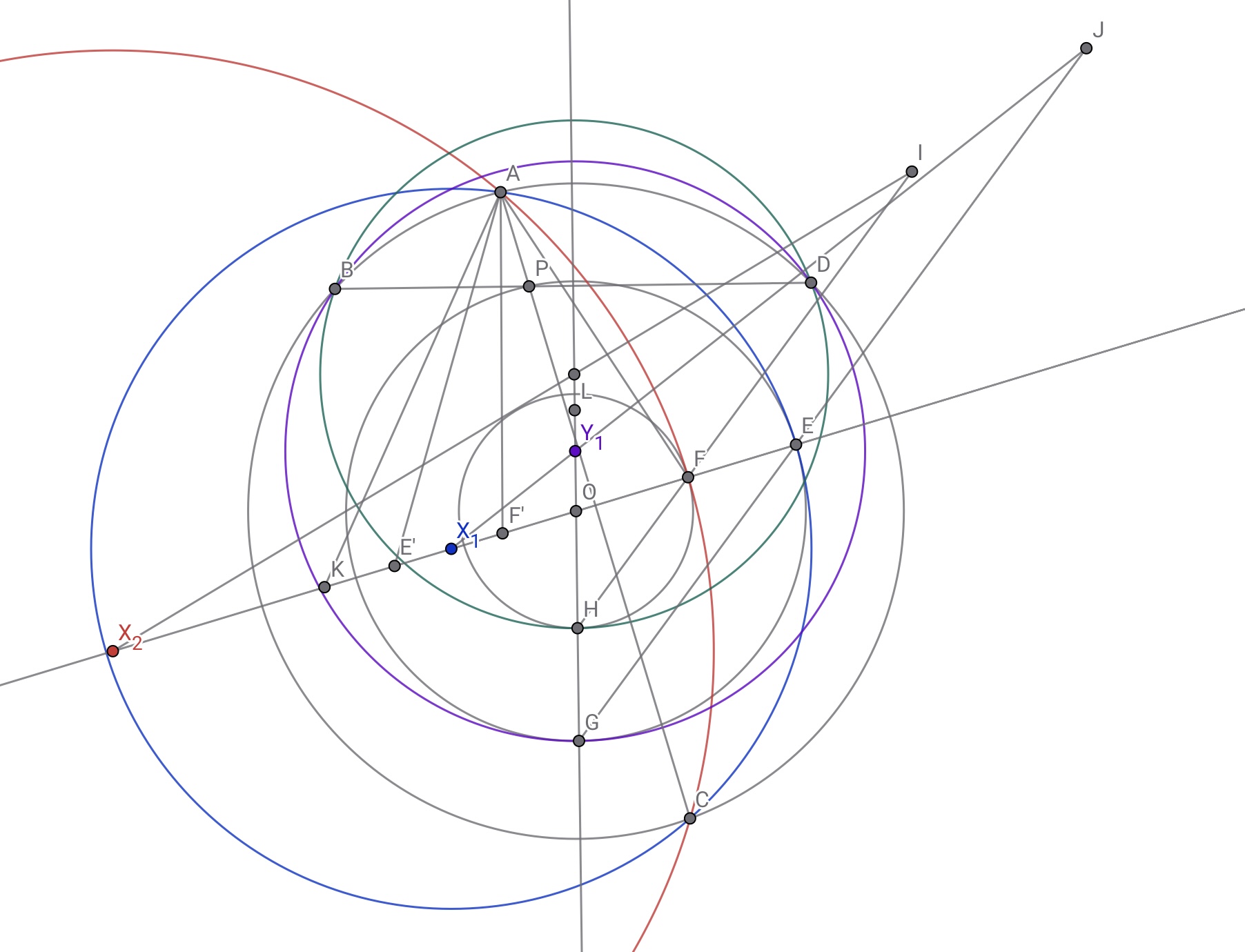図はゴチャついているがやってることはシンプル
直線$BD$に関して点$G$と対称な点を$G'$とすれば同様の計算から$BH^2=HL\cdot HG', OL=\dfrac{BO^2-OG\cdot OH}{HG'}$となるので
$\dfrac{IF}{HI}\cdot\dfrac{KO}{FK}\cdot\dfrac{LH}{OL}=1$がわかる．したがってメネラウスの定理の逆より3点$I,K,L$は同一直線上である．以上から6点$I,J,K,L,M,N$は同一直線上． ■
さらに問題を解きほぐしていく前に，以下の補題を示しておきます．次に何をするかわかりやすくする意味も込めて．
三角形$ABC$において角$ABC$の二等分線と辺$BC$の交点を$D$とし，点$B,C,D$を中心として点$A$を通る円を順に$\Omega_B, \Omega_C, \Omega_D$とする．円$\Omega_D$上に点$P$をとると$\dfrac{Pow_{\Omega_B}(P)}{Pow_{\Omega_C}(P)}=\dfrac{AB}{AC}$が成り立つ．
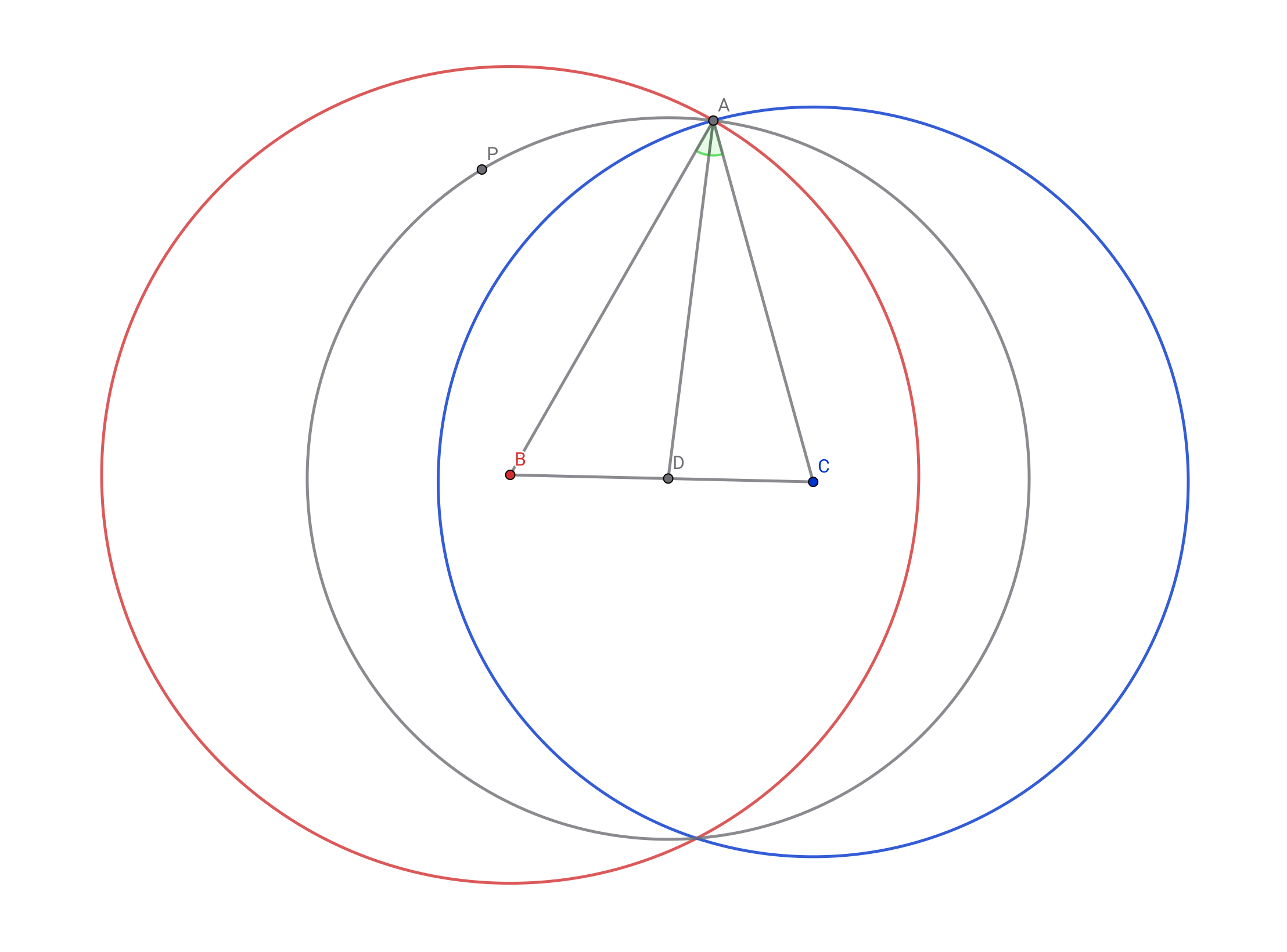名前がついていそうな気もする
直線$BC$に関して点$A$と対称な点を$E$とする．点$A$における円$\Omega_D$の接線が円$\Omega_B, \Omega_C$と再び交わる点を順に$X,Y$とし，直線$AP$が円$\Omega_B, \Omega_C$と再び交わる点を順に$Q,R$とする．角度追跡から三角形$EPA, EQX, ERY$は相似なので，三角形$EQP$と$EXA$は相似であり三角形$ERP$と$EYA$も相似である．また三角形$BXA$と$CAY$も相似なので
$\dfrac{Pow_{\Omega_B}(P)}{Pow_{\Omega_C}(P)}=\dfrac{PA\cdot PQ}{PA\cdot PR}=\dfrac{AX\cdot EP}{EA}\cdot\dfrac{EA}{AY\cdot EP}=\dfrac{AX}{AY}=\dfrac{AB}{AC}$ ■
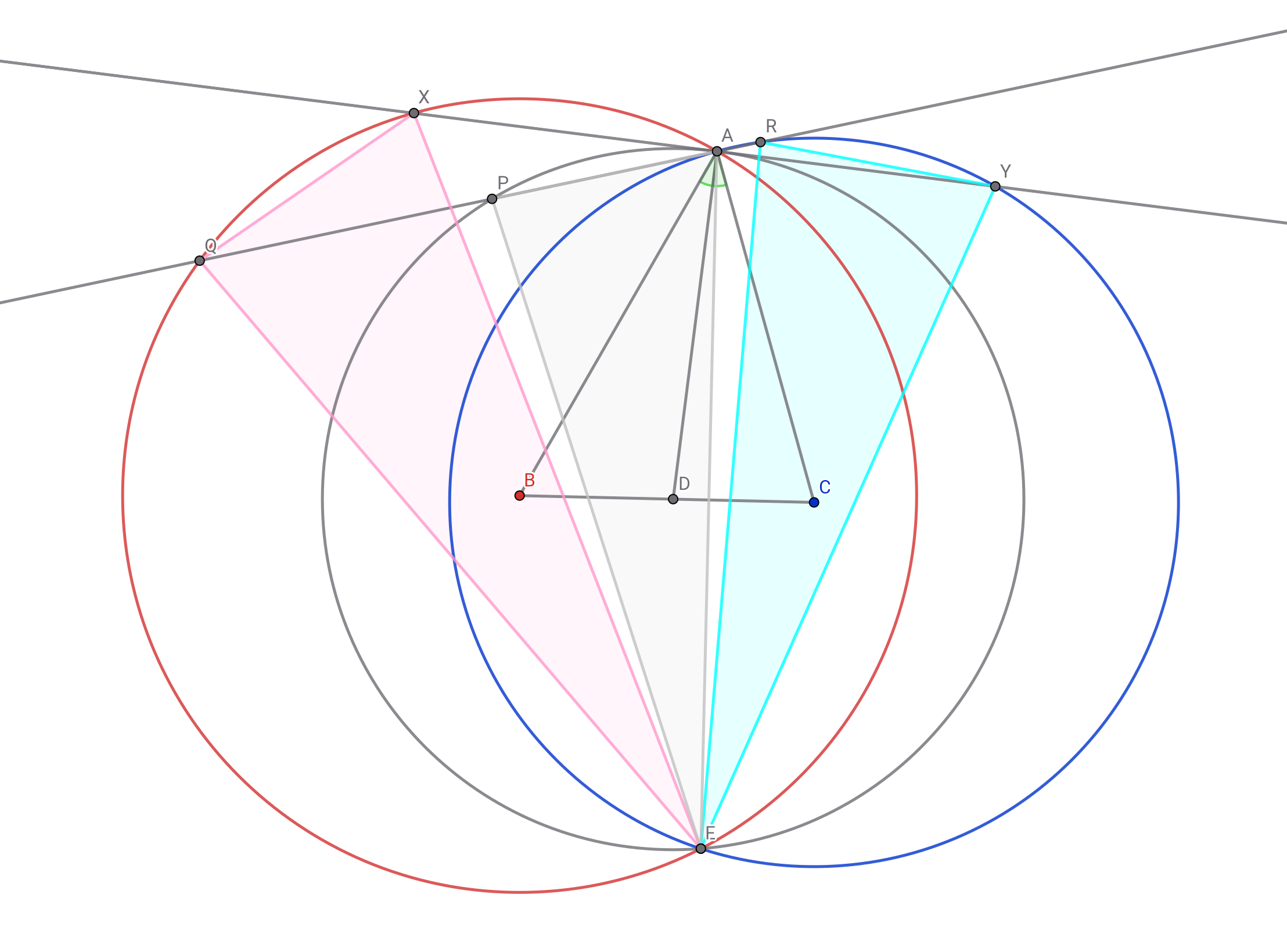The 構図
さらに補題に対する理解を深めます．
補題3の図において，点$P$を中心とする反転により円$\Omega_B, \Omega_C$が移る2円は半径が等しい．
直線$PB$と円$\Omega_B$の交点を$F,G$とし，直線$PC$と円$\Omega_C$の交点を$H,I$とする．下図のようであったとすると（正確性を厳密にするなら有向性を付与するべきだが）
$\Omega_B$を半径$r$の円で反転した後の円の半径$r_B$は
$r_B=\dfrac{r^2}{PF}+\dfrac{r^2}{PG}=\dfrac{r^2FG}{PF\cdot PG}=\dfrac{2r^2AB}{Pow_{\Omega_B}(P)}$
$\Omega_C$を半径$r$の円で反転した後の円の半径$r_C$は
$r_C=\dfrac{r^2}{PH}-\dfrac{r^2}{PI}=\dfrac{r^2HI}{PH\cdot PI}=\dfrac{2r^2AC}{Pow_{\Omega_C}(P)}$
補題3よりこの2つは等しい． ⬛︎
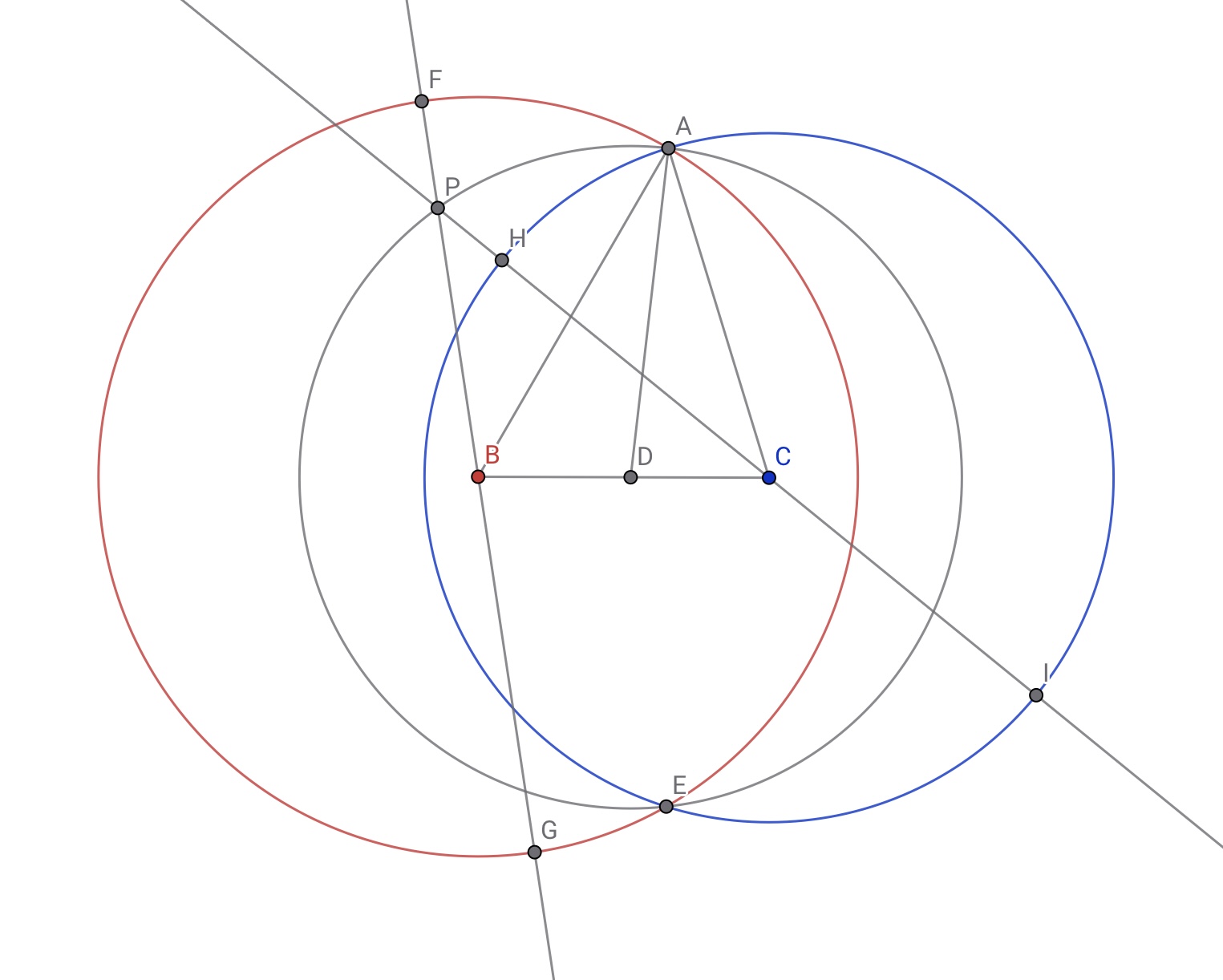力技
これらの補題を適用する前に問題の図に対する理解を深めておきましょう．
4円$\gamma_1,\gamma_2,\delta_1,\delta_2$のうちの2円の根軸は全て点$P$を通る．
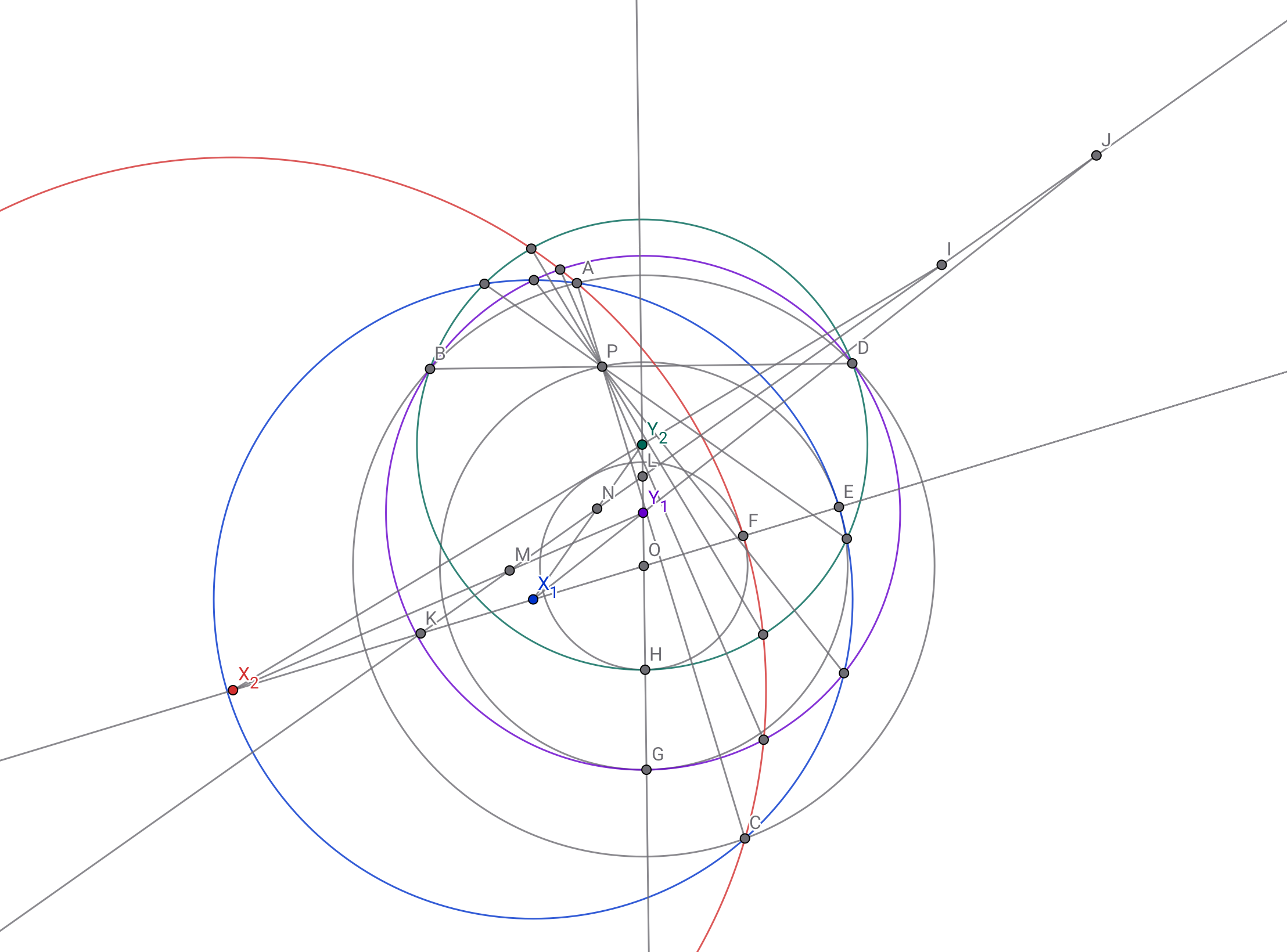渾身の……
円$\gamma_1$と$\gamma_2$，$\delta_1$と$\delta_2$の根軸はそれぞれ直線$AC,BD$なので明らか．
円$\gamma_i$と円$\delta_j$と円$\omega_0$について根心が点$P$となることから円$\gamma_i$と円$\delta_j$の根軸は点$P$を通る． ⬛︎
ある程度材料が揃ってきたので，今回の解法の中心部分の一つを提示していきます．仰々しく言いましたが内容は思いつきやすく示し方も一本道です．
$\cdot$点$I$を中心として，円$\gamma_2$と$\delta_2$の2交点を通る円
$\cdot$点$J$を中心として，円$\gamma_1$と$\delta_1$の2交点を通る円
$\cdot$点$K$を中心として，円$\gamma_1$と$\gamma_2$の2交点を通る円
$\cdot$点$L$を中心として，円$\delta_1$と$\delta_2$の2交点を通る円
$\cdot$点$M$を中心として，円$\gamma_2$と$\delta_1$の2交点を通る円
$\cdot$点$N$を中心として，円$\gamma_1$と$\delta_2$の2交点を通る円
の6円は全て同じ2点を通る．
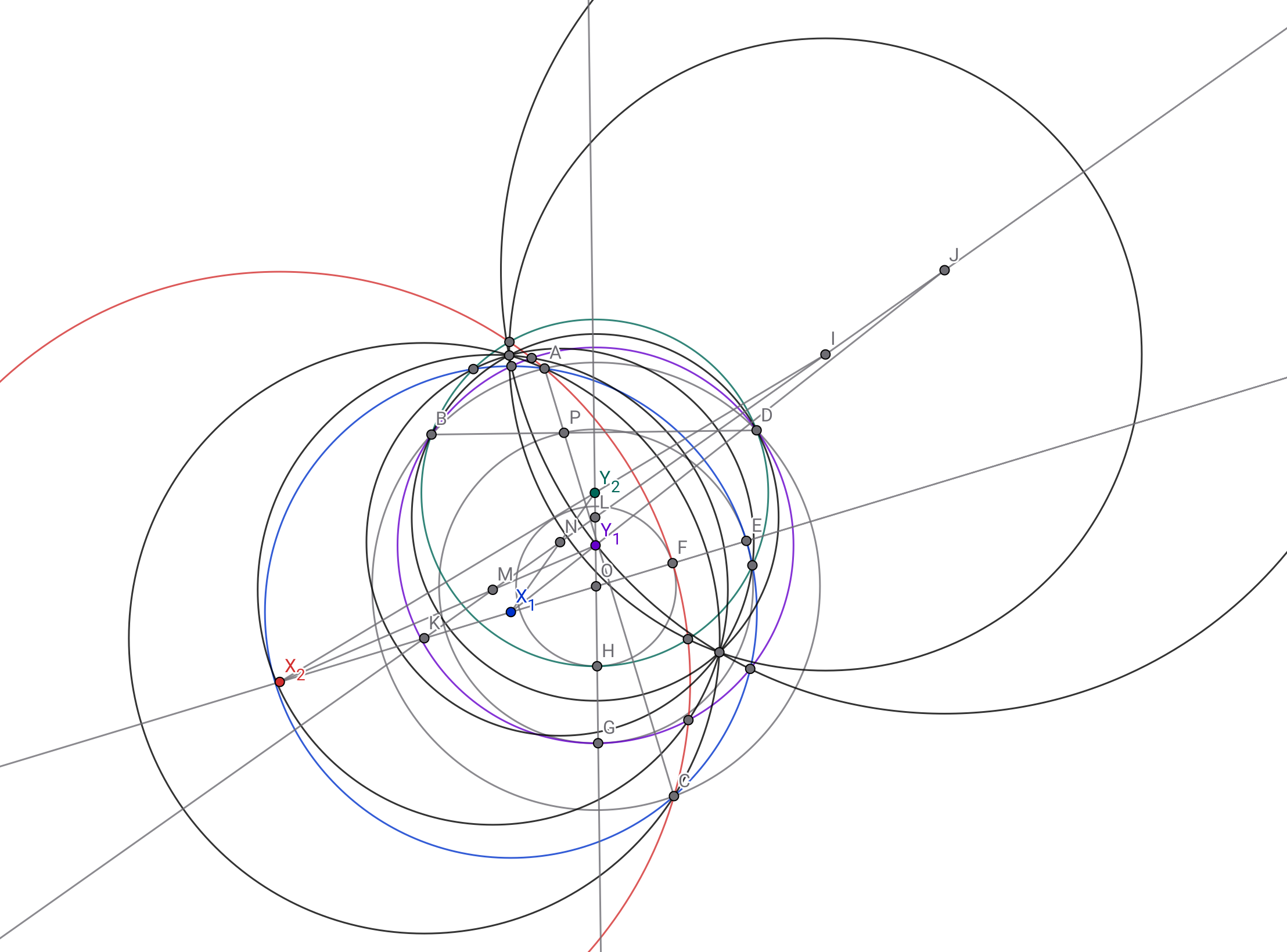円が……円が多すぎる……！
補題3のような円を作れるだけ作ってみよう，という安直な作図です．命題5の根心と命題2の直線の関係性をうまく使っていきましょう．
点$P$から直線$IJ$に下ろした垂線の脚を点$Q$とする．点$P$を通り直線$IJ$に垂直な直線上に異なる2点$R,S$を
$QR^2=QS^2=AP\cdot CP+QP^2$
を満たすようにとれば，$RP\cdot RS=AP\cdot CP$より$ARCS$は円に内接し，この円の中心は線分$AC,RS$それぞれの垂直二等分線の交点，すなわち点$K$となる．命題2で得られた共通弦全てで同様の議論ができ，件の6円は全て点$R,S$を通ることが言える． ⬛︎
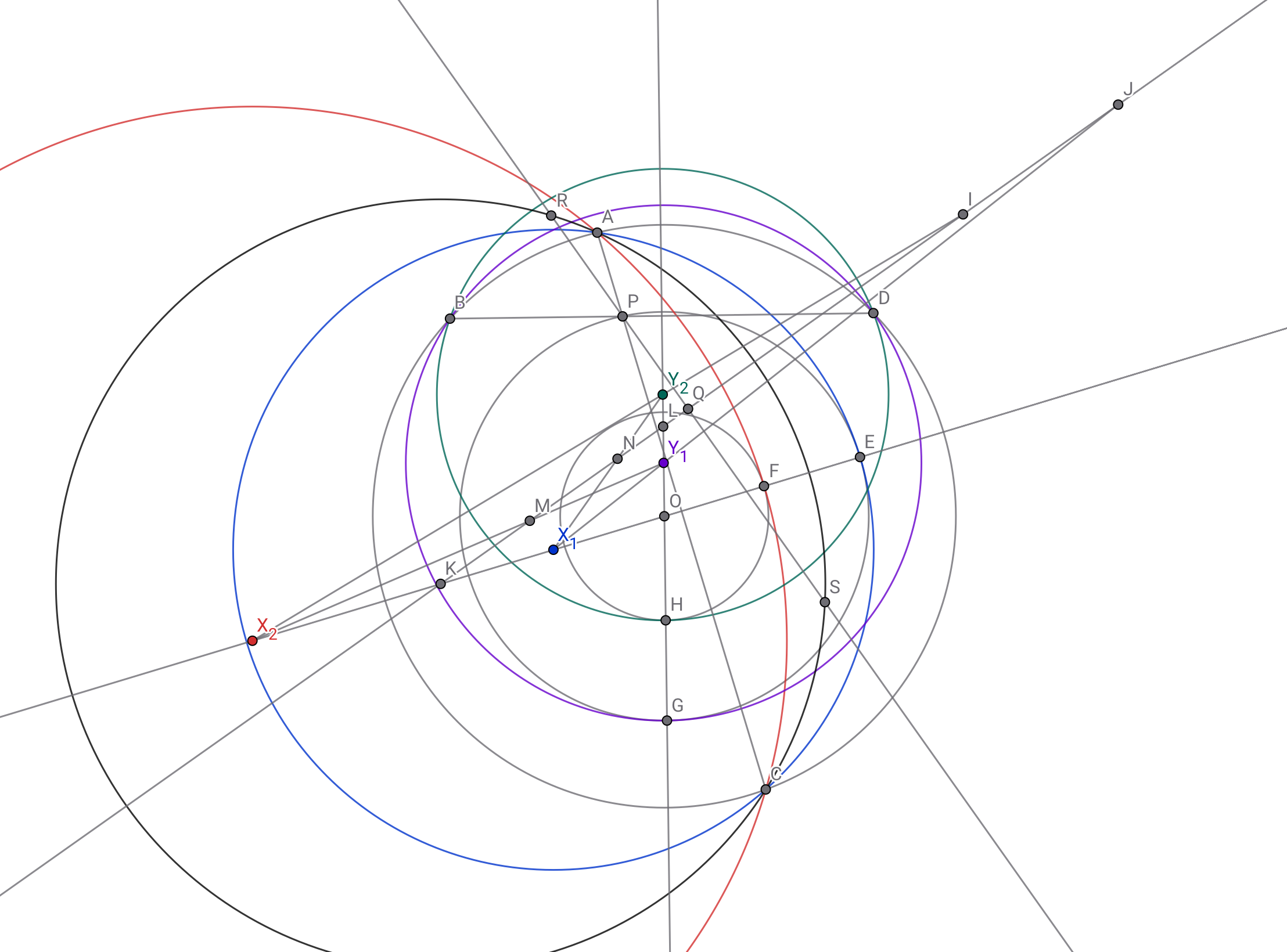同じことを6回確認するだけ
ここまでを合わせた命題を提示しておきます．
点$R$を中心とする反転により，円$\gamma_1,\gamma_2,\delta_1,\delta_2$は半径の等しい4円に移る．
証明は補題4を繰り返すことで終わるので割愛します．
さて，この反転により円$\gamma_1,\gamma_2,\delta_1,\delta_2$が特殊な関係になりました．もとのこの4円に接する円が存在するのであれば，反転を施した後の4円にも接する円が当然存在します．反転後の4円の中心と，この4円に接する円の中心との距離は全て「この4円に接する円の半径」±「反転後の4円の等しい半径」になるはずであり，逆に反転後の4円の中心が同一円周上にあることを示すことが出来れば$\gamma_1,\gamma_2,\delta_1,\delta_2$に接する円も構成できるので解決ということになります．
これに向けた第一歩目から．
点$R$を中心とする（適当な）反転で$\gamma_1,\gamma_2,\delta_1,\delta_2$が移った後の円の中心を順に$V_1,V_2,W_1,W_2$とすると
$RI//V_2W_2, RJ//V_1W_1, RK//V_1V_2,$
$RL//W_1W_2, RM//V_2W_1, RN//V_1W_2$
が成り立つ．
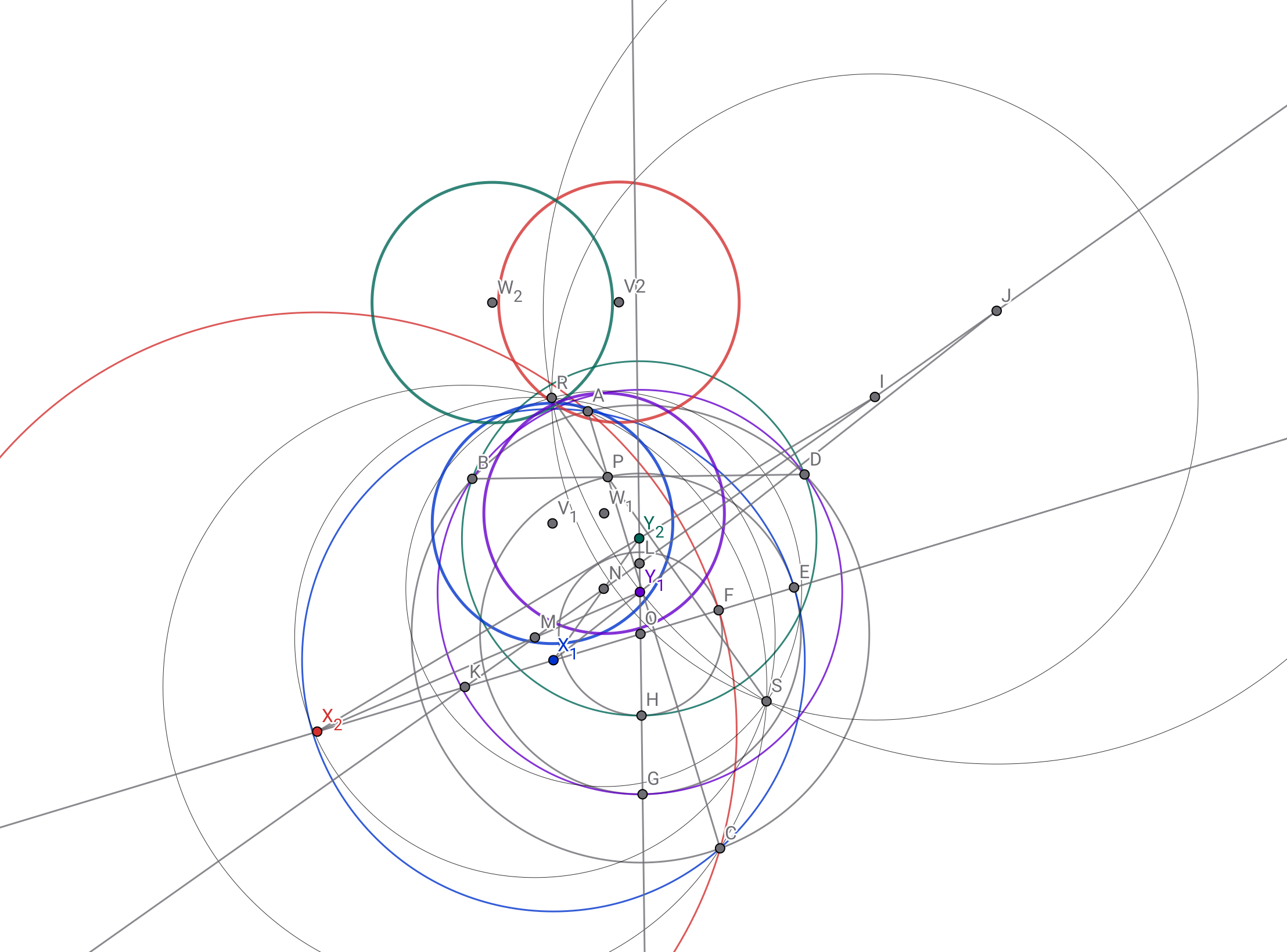求：図のセンス
$\angle ARC$の二等分線と直線$X_1X_2$の交点を$K’$とする．$K’$は円$RASC$上にあるため$KR=KK’$となり，直線$RK$は直線$KK’$を直線$RK’$に関して対称移動させた直線に平行となる．また，$V_1$を中心とする円と$V_2$を中心とする円の根軸は直線$AC$を直線$RK’$に関して対称移動させた直線と平行である．直線$KK’$と直線$AC$は垂直なので直線$RK$と上記の根軸も垂直となり，したがって直線$RK$と直線$V_1V_2$は平行となる．同様の議論で他の並行も示される． ⬛︎
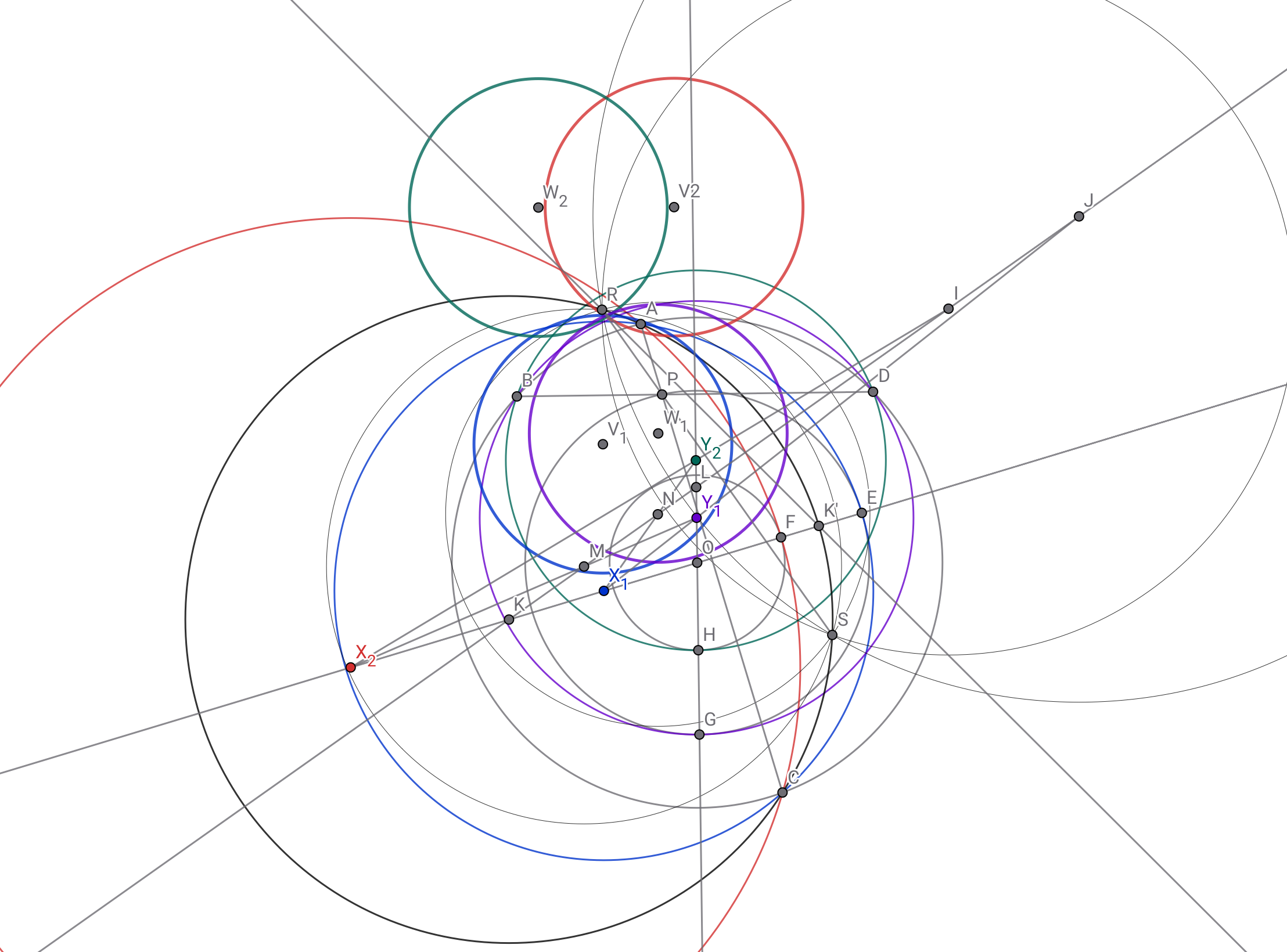同じことを繰り返せば……という常套句
$V_1V_2W_1W_2$の共円を角度から示す場合には直線$RI,RJ,RK,RL,RM,RN$について考えれば良いことがわかります．
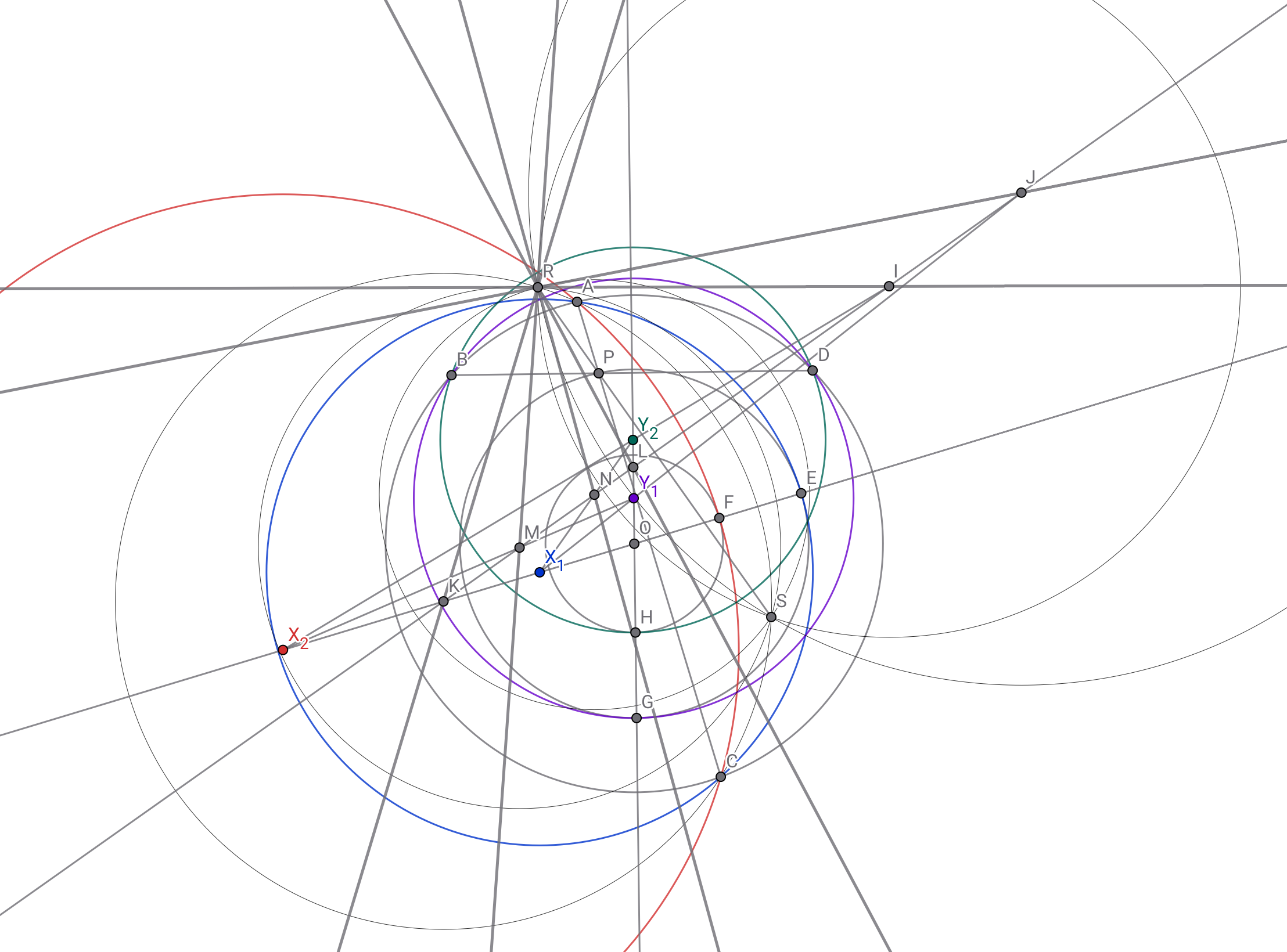射影幾何で捉えられるんだろうな，という思い
もっと言えば$\angle KRI+\angle LRJ=180\degree$が示されれば良いわけですが，その前にいくつかの有名知識を補題として提示させください．お願いします．この通りです．
三角形$ABC$の$\angle BAC$の内角二等分線と辺$BC$の交点を$D$，外角二等分線と直線$BC$の交点を$E$とすれば
$AD^2=AB\cdot AC-BD\cdot CD,AE^2=BE\cdot CE-AB\cdot AC$
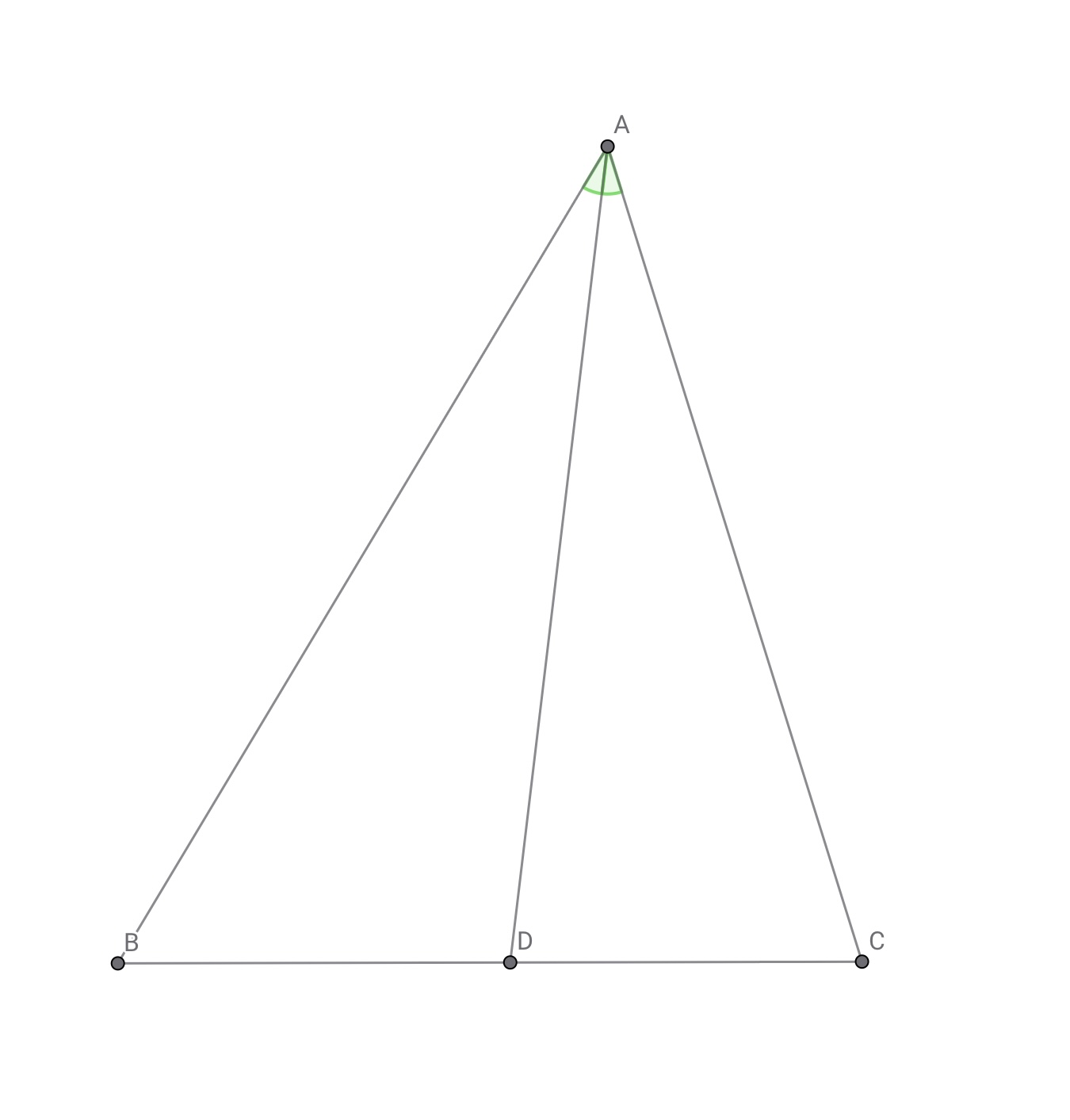
三角形$ABC$の内心を$I$，内接円と辺$BC$の接点を$D$とすれば
三角形$ABC$の面積を$[ABC]$で表すとすると
$[ABC]=BD\cdot CD\cdot cot\angle IAC$
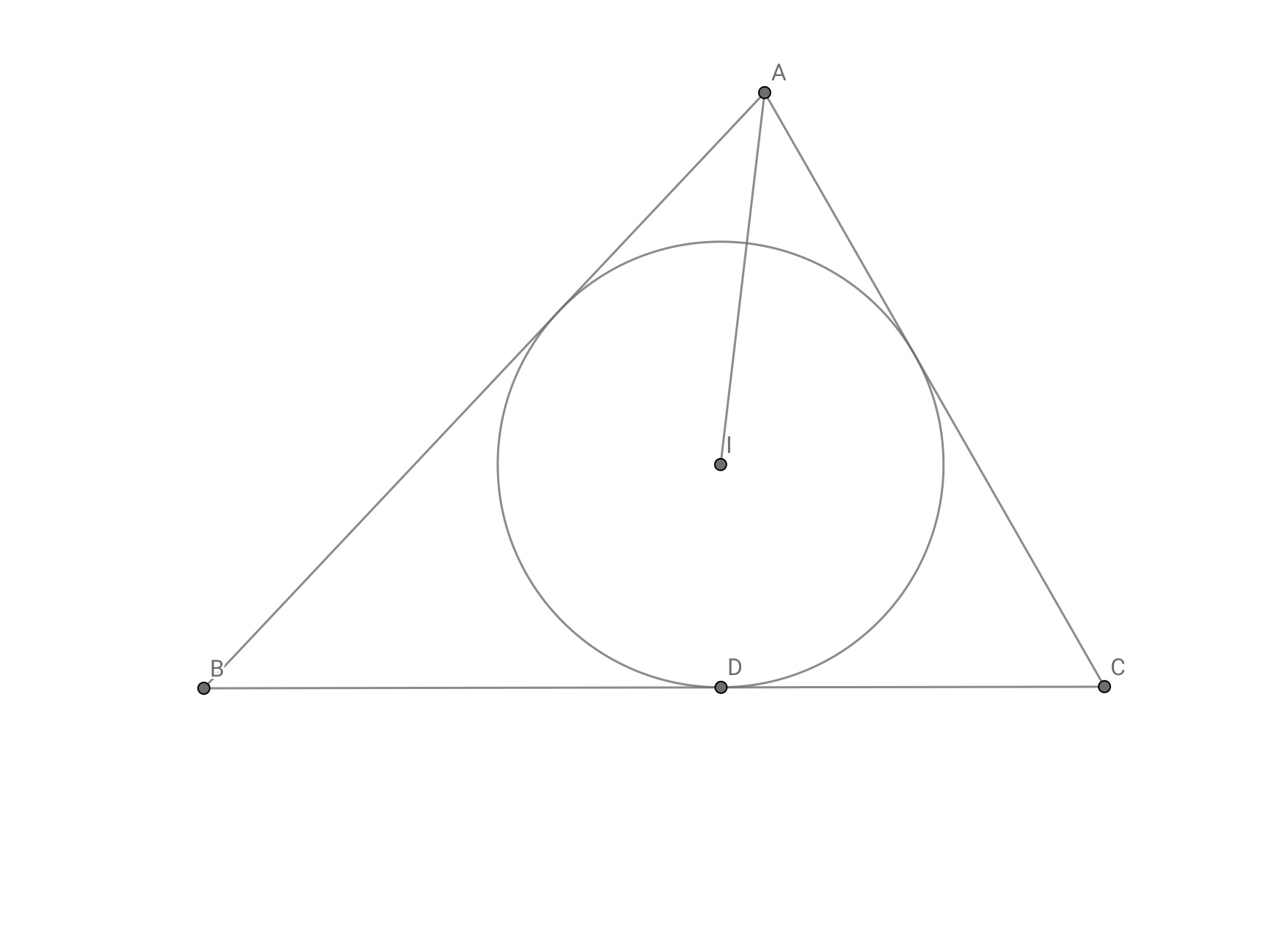
証明は読者の演習としたい，と言いたいだけです．ここで示した有名事実を用いて前哨戦となる共線関係を示しておきましょう．
線分$EF,GH$の中点を順に展開$U,V$とし，直線$X_1Y_1$と$X_2Y_2$の交点を$Z$とすれば，3点$U,V,Z$は同一直線上．
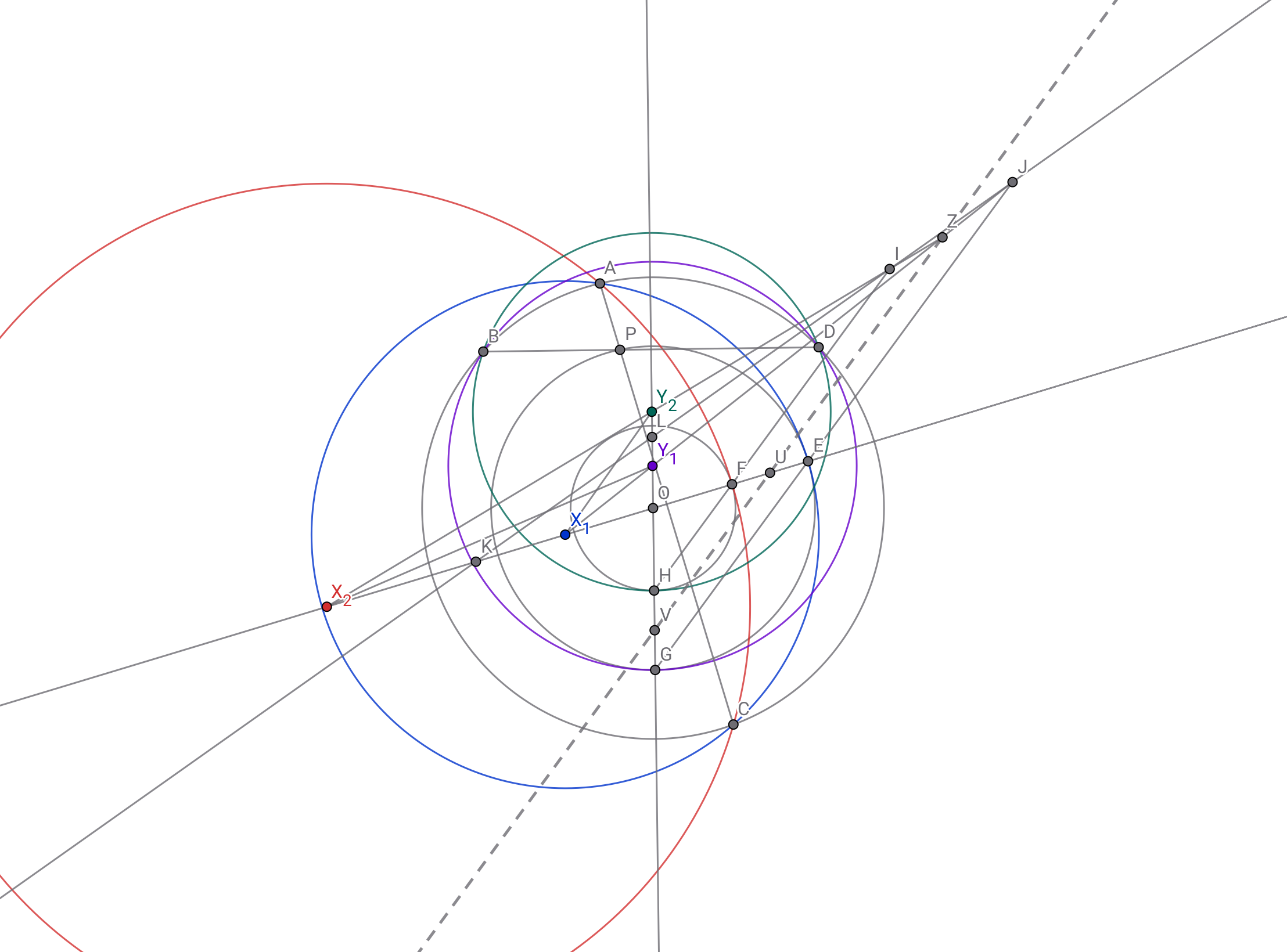中点がくると無限遠点を探したくなりがち
命題2の証明で用いた計算結果も登場します．
定義とメネラウスの定理から
$\dfrac{ZY_1}{X_1Z}\cdot\dfrac{Y_2O}{Y_1Y_2}\cdot\dfrac{X_2X_1}{OX_2}=1$であり
$\dfrac{ZY_1}{X_1Z}=\dfrac{OX_2}{OY_2}\cdot\dfrac{Y_1Y_2}{X_1X_2}=\dfrac{\frac{FX_2}{AF^2}}{\frac{HY_2}{BH^2}}\cdot\dfrac{Y_1Y_2}{X_1X_2}=\dfrac{BD\tan{\angle HBD}}{AC\tan{\angle FAC}}\cdot\dfrac{Y_1Y_2}{X_1X_2}$
$=\dfrac{[BY_1Y_2]\tan{\angle HBD}}{[AX_1X_2]\tan{\angle FAC}}=\dfrac{(BY_1+BY_2-Y_1Y_2)(BY_1-BY_2+Y_1Y_2)}{(AX_1+AX_2-X_1X_2)(AX_1-AX_2+X_1X_2)}$
$=\dfrac{(Y_1G+Y_2H-Y_1Y_2)GH}{(X_1E+X_2F-X_1X_2)EF}=\dfrac{2Y_1V}{2X_1U}$から
$\dfrac{ZY_1}{X_1Z}\cdot\dfrac{VO}{Y_1V}\cdot\dfrac{UX_1}{OU}$となるのでメネラウスの定理の逆から示される． ⬛︎
これらを使って先ほどの命題を示しましょう．
$\angle KRI+\angle LRJ=180\degree$が成り立つ．
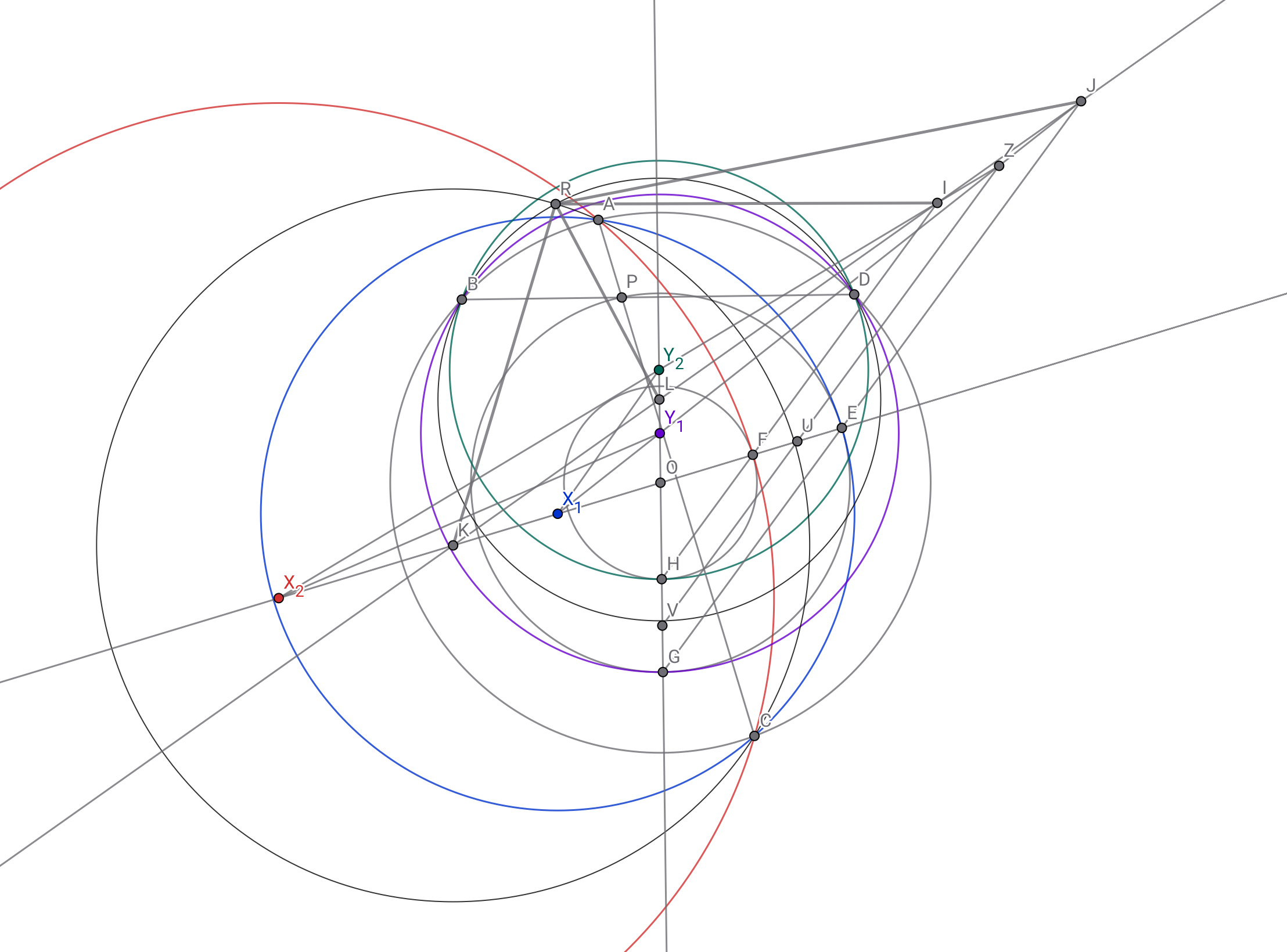△KRLと△KIJの外接円が接するという表現もあり
$X_1Y_2$と$X_2Y_1$の交点を$W$とする．
$HF//GE$より$\dfrac{IJ}{KI}=\dfrac{FE}{KF}, \dfrac{IJ}{LJ}=\dfrac{HG}{LG}$ なので
$\dfrac{LJ}{KI}=\dfrac{LG}{KF}=\dfrac{GY_1+Y_1L}{FX_2-X_2K}=\dfrac{GY_1+\frac{Y_1Y_2\cdot Y_1G}{Y_1G+Y_2H}}{FX_2-\frac{X_1X_2\cdot X_2F}{X_2F+X_1E}}$
$=\dfrac{GY_1}{FX_2}\cdot \dfrac{(X_1E+X_2F)(Y_1G+Y_2H+Y_1Y_2)}{(Y_1G+Y_2H)(X_1E+X_2F-X_1X_2)}$
$=\dfrac{GY_1}{FX_2}\cdot \dfrac{(X_1E+X_2F)Y_2V}{(Y_1G+Y_2H)X_1U}$
また補題9より
$RI^2=X_2I\cdot Y_2I-X_2F\cdot Y_2H=X_2Y_2^2\cdot\dfrac{X_2F\cdot Y_2H}{(X_2F-Y_2H)^2}-X_2F\cdot Y_2H$
$RJ^2=X_1Y_1^2\cdot\dfrac{X_1E\cdot Y_1G}{(X_1E-Y_1G)^2}-X_1E\cdot Y_1G$
$RK^2=X_2F\cdot X_1E-X_1X_2^2\cdot\dfrac{X_2F\cdot X_1E}{(X_2F+X_1E)^2}$
$RL^2=Y_1G\cdot Y_2H-Y_1Y_2^2\cdot\dfrac{Y_1G\cdot Y_2H}{(Y_1G+Y_2H)^2}$
したがって
$\dfrac{RJ^2RL^2}{RI^2RK^2}=\dfrac{Y_1G^2}{X_2F^2}\cdot\dfrac{(X_2F-Y_2H)^2(X_2F+X_1E)^2}{(X_1E-Y_1G)^2(Y_1G+Y_2H)^2}\cdot\dfrac{(X_1Y_1+X_1E-Y_1G)(X_1Y_1-X_1E+Y_1G)(Y_1G+Y_2H+Y_1Y_2)(Y_1G+Y_2H-Y_1Y_2)}{(X_2Y_2+X_2F-Y_2H)(X_2Y_2-X_2F+Y_2H)(X_2F+X_1E+X_1X_2)(X_2F+X_1E-X_1X_2)}$
$=\dfrac{Y_1G^2}{X_2F^2}\cdot\dfrac{(X_2F-Y_2H)^2(X_2F+X_1E)^2}{(X_1E-Y_1G)^2(Y_1G+Y_2H)^2}\cdot\dfrac{[OX_1Y_1]\cdot Y_2V\cdot Y_1V}{[OX_2Y_2]\cdot X_2U\cdot X_1U}\cdots ①$
ここで$\dfrac{Y_1G^2}{X_2F^2}\cdot\dfrac{(X_2F-Y_2H)^2(X_2F+X_1E)^2}{(X_1E-Y_1G)^2(Y_1G+Y_2H)^2}=\alpha$とおけば
$①=\alpha\cdot\dfrac{[OX_1Y_1]}{[OX_2Y_2]}\cdot\dfrac{ZY_2}{X_2Z}\cdot\dfrac{ZY_1}{X_1Z}=\alpha\cdot\dfrac{[OX_1Y_1][ZY_1Y_2]}{[OX_2Y_2][ZX_1X_2]}=\alpha\cdot\dfrac{(X_1O\cdot X_1Y_1)(Y_2Y_1\cdot Y_2Z)}{(Y_2O\cdot Y_2X_2)(X_1X_2\cdot X_1Z)}$
$=\alpha\cdot\dfrac{X_1O\cdot Y_2Y_1}{X_2X_1\cdot OY_2}\cdot\dfrac{Y_2Z\cdot X_1Y_1}{X_2Y_2\cdot ZX_1}=\alpha\cdot (\dfrac{WY_1}{X_2W})^2$
より
$\dfrac{KI}{LJ}\cdot\dfrac{RJ\cdot RL}{RI\cdot RK}=\dfrac{X_1U}{Y_2V}\cdot\dfrac{X_2F-Y_2H}{X_1E-Y_1G}\cdot\dfrac{WY_1}{X_2W}=\dfrac{X_1U}{Y_2V}\cdot\dfrac{X_2U-Y_2V}{X_1U-Y_1V}\cdot\dfrac{WY_1}{X_2W}$
$=\dfrac{X_1Z}{Y_1X_1}\cdot\dfrac{Y_2X_2}{ZY_2}\cdot\dfrac{WY_1}{X_2W}=1$
なので$\dfrac{LJ}{KI}=\dfrac{RJ\cdot RL}{RI\cdot RK}$
$\angle JRL=\angle IRK$だとすると$\angle IRJ=\angle KRL$となるがこれは成り立たず(議論は省略……)，$\angle KRI+\angle LRJ=180\degree$となる． ⬛︎
以上の議論をまとめると，元の問題が示されます．
煩雑な計算と愚直な議論に頼ればほぼ示せるのですが，やはり公式解説内のように見通しの良い議論を学びたいですね．
