【超フィルター論 ①】超フィルターによる位相空間の定義・自由なコンパクトハウスドルフ空間
【更新】
2025/08/10 続きを書いているためタイトルを変更
元タイトル:超フィルターによる位相空間論 ~「結局『位相空間』とは何なのか?」を根本から理解する考え方~
2025/10/11 全体的に修正
各章の概要
一章:超フィルターの全体が極限・連続と呼ぶにふさわしい構造を持つことを示します
二章:位相空間と超フィルターの関係を確認し、超フィルターのみを用いた位相空間の定義を与えます
三章:一章で定めた構造が集合の圏$\mathbf{Set}$からコンパクトハウスドルフ空間の圏$\mathbf{KH}$への自由関手であることを示します
1.超フィルターの基礎
1-1.超フィルターの定義・存在・特徴付け
この節では、有限交叉族を通して超フィルターの定義と特徴付けを行います。
$X:$集合$,\mathcal{B}$を$X$の部分集合の空でない族とする。
$\mathcal{B}$が有限交叉族である$\stackrel{\mathrm{def}}{ \Leftrightarrow }$任意の$A_1,A_2,\cdots,A_n\in\mathcal{B}$に対して$\bigcap\limits_{k=1}^nA_k\neq\varnothing $
$X:$無限集合に対して、$X$の補有限集合の全体$\{A\subset X\ |\ X \setminus A$が有限集合$\}$は有限交叉族です。
$(\because)A_1,A_2,\cdots,A_n$を$X$の補有限集合とする。
この時
$X\backslash(\bigcap\limits_{k=1}^nA_k)=\bigcup\limits_{k=1}^n(X\backslash A_k)$
は有限集合なので$\bigcap\limits_{k=1}^nA_k$は補有限集合である。
特に$\bigcap\limits_{k=1}^nA_k\neq\varnothing $である。$\square$
これを$X$のフレシェフィルターと呼びます。
名前の通り$X$のフレシェフィルターは$X$のフィルターになりますが、本記事ではフィルターには触れません。
$X:$集合$,\mathcal{U}$を$X$の有限交叉族とする。
$\mathcal{U}$が超フィルターである$\stackrel{\mathrm{def}}{ \Leftrightarrow }$任意の有限交叉族$\mathcal{B}$に対して$\mathcal{U}\subset\mathcal{B}$ならば$\mathcal{U}=\mathcal{B}$
と定める。
$X$の超フィルターの全体が成す集合を$\mathrm{Ult}(X)$と書く。
つまり超フィルターとは、Xの有限交叉族全体の包含関係についての極大元です。従って、異なる超フィルター同士は互いに包含関係にありません。
超フィルターはツォルンの補題によって存在が保証されます。
$X:$集合$,\mathcal{B}$を$X$の有限交叉族とする。
この時、$\mathcal{B}$を含む$X$の超フィルターが存在する。
$\mathbb{M}=\{\mathcal{C}:$有限交叉族$ \ | \ \mathcal{B}\subset\mathcal{C}\}$とし、包含関係を順序として順序集合とみなす。
$\mathbb{J}\subset\mathbb{M} $を空でない全順序部分集合とする。
$\mathcal{D}=\bigcup\limits_{\mathcal{C}\in\mathbb{J}}\mathcal{C}$とする。
この時$\mathcal{D}$は有限交叉族である。
$(\because)A_1,A_2,\cdots,A_n\in\mathcal{D}$を任意に取る。
$\mathcal{C_1},\mathcal{C_2},\cdots,\mathcal{C_n}\in\mathbb{J}$が存在して、任意の$i=1,2,\cdots,n$に対して$A_i\in\mathcal{C_i}$となる。
$\mathbb{J}$は包含関係について全順序なので、$\mathcal{C'}=max\{\mathcal{C_1},\mathcal{C_2},\cdots,\mathcal{C_n}\}$とすれば$A_1,A_2,\cdots,A_n\in\mathcal{C'}$となる。
$\mathcal{C'}$は有限交叉族なので$\bigcap\limits_{k=1}^nA_k\neq\varnothing $となる。
よって$\mathcal{D}$は有限交叉族である。
$\mathcal{D}$の定義により$\mathcal{D}$は$\mathbb{M}$に於ける$\mathbb{J}$の上界である。
従って$\mathbb{M}$は任意の空でない全順序部分集合が上界を持つので、ツォルンの補題により極大元を持つ。$\square$
$X$を無限集合とすると、フレシェフィルターを含む$X$の超フィルターが存在します。
フレシェフィルターを含む超フィルターを自由な超フィルターと呼びます。
なお自由な超フィルターは、ツォルンの補題によって存在が保障されるため、具体的に記述することができません。
また一般に無限集合$X$に対して、自由な超フィルターの全体の成す集合の濃度は$2^{2^X}$と等しくなります。(証明は6を参照)
つまり自由な超フィルターは十分にたくさん存在します。
超フィルターの特徴付けを行うため、先に簡単な補題を示します。
$X:$集合$,\mathcal{B}$を$X$の有限交叉族とする。
この時以下が成立する。
(1) $\mathcal{B}\cup\{X\}$は有限交叉族
(2) 任意の$A,A'\in\mathcal{B} $に対して$\mathcal{B}\cup\{A\cap A'\}$は有限交叉族
(3) 任意の$A,A'\subset X$に対して、$A\cup A'\in\mathcal{B}$ならば$\mathcal{B}\cup\{A\},\mathcal{B}\cup\{A'\}$の内いずれか片方は有限交叉族
- $C_1,C_2,\cdots,C_n\in\mathcal{B}$とすると
$(\bigcap\limits_{k=1}^nC_k)\cap X=\bigcap\limits_{k=1}^nC_k\neq\varnothing $
となるため$\mathcal{B}\cup\{X\}$は有限交叉族 - $C_1,C_2,\cdots,C_n\in\mathcal{B}$とすると$A,A'\in\mathcal{B} $により
$(\bigcap\limits_{k=1}^nC_k)\cap(A\cap A')\neq\varnothing $
となるため$\mathcal{B}\cup\{A\cap A'\}$は有限交叉族 - $A,A'\subset X$が存在して、$A\cup A'\in\mathcal{B}$かつ$\mathcal{B}\cup\{A\},\mathcal{B}\cup\{A'\}$のいずれも有限交叉族にならないと仮定する。
$\mathcal{B}\cup\{A\}$は有限交叉族でないので、$C_1,C_2,\cdots,C_n\in\mathcal{B}$が存在して$(\bigcap\limits_{k=1}^nC_k) \cap A=\varnothing $となる。
同様に$C'_1,C'_2,\cdots,C'_m\in\mathcal{B}$が存在して$(\bigcap\limits_{l=1}^mC'_l) \cap A'=\varnothing $となる。
この時
$(\bigcap\limits_{k=1}^nC_k)\cap (\bigcap\limits_{l=1}^mC'_l)\cap (A\cup A')\subset ((\bigcap\limits_{k=1}^nC_k)\cap A)\cup ((\bigcap\limits_{l=1}^mC'_l)\cap A')=\varnothing$
となり$\mathcal{B} $が有限交叉族であることに矛盾する。
従って$\mathcal{B}\cup\{A\},\mathcal{B}\cup\{A'\}$の内いずれか片方は有限交叉族である。$\square$
有限交叉族の包含関係ではなく、集合の演算のみを用いて超フィルターを定義すると以下のようになります。
$X:$集合$,\mathcal{U}$を$X$の部分集合の族とする。
この時、$\mathcal{U}$が超フィルターであることと、以下の四条件を満たすこととは互いに同値である。
(1) $\varnothing \notin\mathcal{U}$
(2) $X\in\mathcal{U}$
(3) 任意の$A,A'\in\mathcal{U} $に対して$ A\cap A'\in\mathcal{U}$
(4) 任意の$A,A'\subset X$に対して$ A\cup A'\in\mathcal{U} \Rightarrow A\in\mathcal{U}$または$A' \in\mathcal{U}$
$X:$集合$,\mathcal{U}$を$X$の超フィルターとする。
- $\mathcal{U}$は有限交叉族なので$\varnothing \notin\mathcal{U}$
- $\mathcal{U}\cup\{X\}$は有限交叉族で$\mathcal{U}\subset\mathcal{U}\cup\{X\}$なので$\mathcal{U}=\mathcal{U}\cup\{X\}$である。
従って$X\in\mathcal{U}\cup\{X\}=\mathcal{U}$ - $A,A'\in\mathcal{U} $とする。
$\mathcal{U}\cup\{A\cap A'\}$は有限交叉族で$\mathcal{U}\subset\mathcal{U}\cup\{A\cap A'\}$なので$\mathcal{U}=\mathcal{U}\cup\{A\cap A'\}$である。
従って$A\cap A'\in\mathcal{U}\cup\{A\cap A'\}=\mathcal{U}$ - $A,A'\subset X, A\cup A'\in\mathcal{U} $とする。
$\mathcal{U}\cup\{A\},\mathcal{U}\cup\{A'\}$の内いずれか片方は有限交叉族である。
$\mathcal{U}\cup\{A\}$が有限交叉族になるならば$\mathcal{U}\subset\mathcal{U}\cup\{A\}$なので$\mathcal{U}=\mathcal{U}\cup\{A\}$であるから$A\in\mathcal{U}\cup\{A\}=\mathcal{U}$となる。
同様に$\mathcal{U}\cup\{A'\}$が有限交叉族になるならば$A'\in\mathcal{U}$となる。$\square$
$X:$集合$,\mathcal{U}$を(1)(2)(3)(4)を満たす$X$の部分集合の族とする。
【$\mathcal{U}$が有限交叉族であること】
$A_1,A_2,\cdots,A_n\in\mathcal{U}$とする。
(3)と帰納法により$\bigcap\limits_{k=1}^nA_k\in\mathcal{U} $である。
(1)により$\bigcap\limits_{k=1}^nA_k\neq\varnothing $である。
従って$\mathcal{U}$は有限交叉族である。
【$\mathcal{U}$が超フィルターであること】
$\mathcal{B}$は有限交叉族$,\mathcal{U}\subset\mathcal{B}$とする。
$A\in\mathcal{B}$とする。
$A\cap A^c=\varnothing$で$\mathcal{B}$は有限交叉族なので$A^c\notin\mathcal{B}$である。
$A^c\notin\mathcal{B}, \mathcal{U}\subset\mathcal{B}$より$A^c\notin\mathcal{U}$である。
(2)により$A\cup A^c=X\in\mathcal{U}$なので、$A^c\notin\mathcal{U}$と(4)により$A\in\mathcal{U}$である。
従って$\mathcal{B}\subset\mathcal{U}$となり、$\mathcal{U}=\mathcal{B}$となるため$\mathcal{U}$は超フィルターである。$\square$
$X:$集合$,\mathcal{U}\in \mathrm{Ult}(X)$とすると、任意の$A\subset X$に対して$A\in\mathcal{U}$または$A^c\in\mathcal{U}$が成り立つ。
$A\subset X$とすると$A\cup A^c=X\in\mathcal{U}$となるため$A\in\mathcal{U}$または$A^c\in\mathcal{U}\square$
$X:$集合$,\mathcal{U}\in \mathrm{Ult}(X)$とする。
この時、任意の$B\subset X$に対して$^{\exists}A\in\mathcal{
U}\ s.t.\ A\subset B\Rightarrow B\in\mathcal{U}$が成り立つ。
$B\subset X,A\in\mathcal{U},A\subset B$とする。
$B^c\in\mathcal{U}$と仮定すると$\varnothing=A\cap B^c\in\mathcal{U}$となり矛盾するため$B^c\notin\mathcal{U}$である。
従って補題4により$B\in\mathcal{U}$である。$\square$
$X:$集合$,x\in X $に対して、
$\langle x \rangle_X \stackrel{\mathrm{def}}{=} \{A\subset X\ |\ x\in A\}$
と定めると、これは明らかに超フィルターになる。
$\langle x \rangle_X$を$x$の固有フィルターと呼ぶ。
なお$X$が有限集合の場合、$X$の超フィルターは固有フィルターのみです。
$X:$集合に対して$\langle\cdot\rangle_X:X\rightarrow \mathrm{Ult}(X)$は単射である。
$x,x'\in X,\langle x \rangle_X=\langle x'\rangle_X$とする。
$\{x\}\in\langle x \rangle_X=\langle x'\rangle_X$より$x'\in\{x\}\Leftrightarrow x=x'$となる。
従って$\langle\cdot\rangle_X$は単射である。$\square$
1-2.超フィルターの像
この節では写像$f:X\rightarrow Y$から写像$\mathrm{Ult}(f):\mathrm{Ult}(X)\rightarrow \mathrm{Ult}(Y)$を構成します。
$X,Y:$集合$,f:X\rightarrow Y,\mathcal{U}\in \mathrm{Ult}(X)$とする。
この時
$\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{U}\}=\{B\subset Y\ |\ ^{\exists}A\in\mathcal{U}\ s.t.\ f(A)\subset B\}\in \mathrm{Ult}(Y)$
が成り立つ。
ここで
$\mathrm{Ult}(f):\mathrm{Ult}(X)\rightarrow \mathrm{Ult}(Y):\mathcal{U}\mapsto\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{U}\}$
と定めて、$\mathrm{Ult}(f)(\mathcal{U})$を$\mathcal{U}$の$f$による像と呼ぶ。
【$f^{-1}(B)\in\mathcal{U}\Rightarrow^{\exists}A\in\mathcal{U}\ s.t.\ f(A)\subset B$】
$B\subset Y,f^{-1}(B)\in\mathcal{U}$とする。
この時$f(f^{-1}(B))\subset B$である。
【$f^{-1}(B)\in\mathcal{U}\Leftarrow^{\exists}A\in\mathcal{U}\ s.t.\ f(A)\subset B$】
$B\subset Y,A\in\mathcal{U},f(A)\subset B$とする。
この時$A\subset f^{-1}(f(A))\subset f^{-1}(B)$と補題4により$f^{-1}(B)\in\mathcal{U}$である。
【$\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{U}\}\in \mathrm{Ult}(Y)$】
$\mathcal{C}=\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{U}\}$と書く。
$\mathcal{C}$が命題3(1)-(4)を満たすことを示す。
- $f^{-1}(\varnothing)=\varnothing\notin\mathcal{U}$より$\varnothing\notin\mathcal{C}$
- $f^{-1}(Y)=X\in\mathcal{U}$より$Y\in\mathcal{C}$
- $B,B'\in\mathcal{C}$とする。
この時$f^{-1}(B\cap B')=f^{-1}(B)\cap f^{-1}(B')\in\mathcal{U}$となるため$B\cap B'\in\mathcal{C}$ - $B,B'\subset Y\ ,\ B\cup B'\in\mathcal{C}$とする。
この時$f^{-1}(B)\cup f^{-1}(B')=f^{-1}(B\cup B')\in\mathcal{U}$となるため
$f^{-1}(B)\in\mathcal{U}$または$f^{-1}(B')\in\mathcal{U}\Leftrightarrow B\in\mathcal{C}$または$B'\in\mathcal{C}$
以上により$\mathcal{C}=\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{U}\}\in \mathrm{Ult}(Y)$である。$\square$
$X,Y:$集合$,\ f:X\rightarrow Y$とします。
一般に$X$の部分集合の族$\mathcal{C}$に対して$Y$の部分集合の族を対応付ける方法には$\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{C}\}$と$\{f(A)\ |\ A\in\mathcal{C}\}$の二通りがあります。
当然$\mathcal{U}\in\mathrm{Ult}(X)$に対しても$\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{U}\}$と$\{f(A)\ |\ A\in\mathcal{U}\}$とを考える必要がありますが、定義4から$\{f(A)\ |\ A\in\mathcal{U}\}$を含む唯一の超フィルターが$\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{U}\}$であることが分かります。
またこれにより$\mathcal{U}\in \mathrm{Ult}(X),\ A\in\mathcal{U}$に対して$f(A)\in \mathrm{Ult}(f)(\mathcal{U})$であることが分かります。
$X,Y:$集合$,f:X\rightarrow Y$に対して$\mathrm{Ult}(f)\circ\langle \cdot\rangle_X=\langle\cdot\rangle_Y\circ f$が成り立つ。
$x\in X$とすると、任意の$B\subset Y$に対して
$B\in \mathrm{Ult}(f)(\langle x \rangle_X)\Leftrightarrow f^{-1}(B)\in\langle x \rangle_X\Leftrightarrow x\in f^{-1}(B)\Leftrightarrow f(x)\in B\Leftrightarrow B\in \langle f(x) \rangle_Y$
となるため$\mathrm{Ult}(f)(\langle x \rangle_X)=\langle f(x) \rangle_Y$である。
従って$\mathrm{Ult}(f)\circ\langle \cdot\rangle_X=\langle\cdot\rangle_Y\circ f$である。$\square$
$X:$集合に対して$\mathrm{Ult}(id_X)=id_{\mathrm{Ult}(X)}$が成り立つ。
任意の$A\subset X,\mathcal{U}\in \mathrm{Ult}(X)$に対して
$A\in \mathrm{Ult}(id_X)(\mathcal{U})\Leftrightarrow id_X^{-1}(A)\in\mathcal{U}\Leftrightarrow A\in id_{\mathrm{Ult}(X)}(\mathcal{U})$
となるため$\mathrm{Ult}(id_X)(\mathcal{U})=id_{\mathrm{Ult}(X)}(\mathcal{U})$である。
従って$\mathrm{Ult}(id_X)=id_{\mathrm{Ult}(X)}$である。$\square$
$X,Y:$集合$,f,g:X\rightarrow Y$とする。
この時$\mathrm{Ult}(f)=\mathrm{Ult}(g)$ならば$f=g$である。
任意の$x\in X$に対して命題7により
$\langle f(x)\rangle_Y=\mathrm{Ult}(f)(\langle x\rangle_X)=\mathrm{Ult}(g)(\langle x\rangle_X)=\langle g(x)\rangle_Y$
となるため命題6により$f(x)=g(x)$である。
従って$f=g$である。$\square$
$X,Y,Z:$集合$,f:X\rightarrow Y,g:Y\rightarrow Z$に対して$\mathrm{Ult}(g\circ f)=\mathrm{Ult}(g)\circ \mathrm{Ult}(f)$が成り立つ。
任意の$\mathcal{U}\in \mathrm{Ult}(X),C\subset Z$に対して
$C\in \mathrm{Ult}(g\circ f)(\mathcal{U})\Leftrightarrow (g\circ f)^{-1}(C)\in\mathcal{U}\Leftrightarrow f^{-1}(g^{-1}(C))\in\mathcal{U}\Leftrightarrow g^{-1}(C)\in \mathrm{Ult}(f)(\mathcal{U})\Leftrightarrow C\in \mathrm{Ult}(g)(\mathrm{Ult}(f)(\mathcal{U}))\Leftrightarrow C\in (\mathrm{Ult}(g)\circ \mathrm{Ult}(f))(\mathcal{U})$
となるため$\mathrm{Ult}(g\circ f)(\mathcal{U})=(\mathrm{Ult}(g)\circ \mathrm{Ult}(f))(\mathcal{U})$である。
従って$\mathrm{Ult}(g\circ f)=\mathrm{Ult}(g)\circ \mathrm{Ult}(f)$である。$\square$
$X,Y:$集合$,\ f:X\rightarrow Y$とする。
この時$\Im\mathrm{Ult}(f)=\{\mathcal{V}\in\mathrm{Ult}(Y)\ |\ \Im f\in\mathcal{V}\}$である。
特に$f:$全射$\Leftrightarrow\mathrm{Ult}(f):$全射である。
【$\Im\mathrm{Ult}(f)\subset\{\mathcal{V}\in\mathrm{Ult}(Y)\ |\ \Im f\in\mathcal{V}\}$】
$\mathcal{V}\in\Im\mathrm{Ult}(f)$とする。
$\mathcal{U}\in\mathrm{ult}(X)$が存在して$\mathrm{Ult}(f)(\mathcal{U})=\mathcal{V}$である。
この時$X\in\mathcal{U}$であるから$\Im f=f(X)\in\mathrm{Ult}(f)(\mathcal{U})=\mathcal{V}$である。
【$\Im\mathrm{Ult}(f)\supset\{\mathcal{V}\in\mathrm{Ult}(Y)\ |\ \Im f\in\mathcal{V}\}$】
$\mathcal{V}\in\mathrm{Ult}(Y),\ \Im f\in\mathcal{V}$とする。
任意の$B_1,B_2,\cdots,B_n\in\mathcal{V}$に対して、$\Im f\cap B_1\cap B_2\cap\cdots\cap B_n\neq\varnothing$であるから、$a\in X$が存在して$f(a)\in B_1\cap B_2\cap\cdots\cap B_n$となる。
この時$a\in f^{-1}(B_1)\cap f^{-1}(B_2)\cap\cdots\cap f^{-1}(B_n)$となるため、$\{f^{-1}(B)\ |\ B\in\mathcal{V}\}$は有限交叉族である。
従って命題1により$\{f^{-1}(B)\ |\ B\in\mathcal{V}\}$を含む$\mathcal{U}\in\mathrm{Ult}(X)$が存在する。
この時任意の$B\in\mathcal{V}$に対して$f^{-1}(B)\in\mathcal{U}\Leftrightarrow B\in\mathrm{Ult}(f)(\mathcal{U})$であるから$\mathcal{V}\subset\mathrm{Ult}(f)(\mathcal{U})$である。
従って超フィルターの極大性により$\mathcal{V}=\mathrm{Ult}(f)(\mathcal{U})\in\Im\mathrm{Ult}(f)$である。
【$f:$全射$\Rightarrow\mathrm{Ult}(f):$全射】
$f$が全射の時、$\Im f=Y$であるから$\Im\mathrm{Ult}(f)=\{\mathcal{V}\in\mathrm{Ult}(Y)\ |\ Y\in\mathcal{V}\}=\mathrm{Ult}(Y)$である。
従って$\mathrm{Ult}(f)$は全射である。
【$f:$全射$\Leftarrow\mathrm{Ult}(f):$全射】
対偶を示す。
$f$が全射でないとする。
$y\in Y\backslash\Im f$を取れば、$\Im f\notin\langle y\rangle_Y$であるから$\langle y\rangle_Y\notin\{\mathcal{V}\in\mathrm{Ult}(Y)\ |\ \Im f\in\mathcal{V}\}=\Im\mathrm{Ult}(f)$である。
従って$\mathrm{Ult}(f)$は全射ではない。$\square$
1-3.ニ重超フィルターの極限
集合$X$に対して$\mathrm{Ult}(\mathrm{Ult}(X))$を$\mathrm{Ult}^2(X)$と書き、$\mathrm{Ult}^2(X)$の元をニ重超フィルターと呼ぶ。
三重,四重,$\cdots$の超フィルターも同様に定義する。
同様に集合$X,Y$と写像$f:X\rightarrow Y$に対して$\mathrm{Ult}(\mathrm{Ult}(f))$を$\mathrm{Ult}^2(f)$と書き、$\mathbf{U}\in \mathrm{Ult}^2(X)$に対して$\mathrm{Ult}^2(f)(\mathbf{U})$を$\mathbf{U}$の像と呼ぶ。
三重,四重,$\cdots$の場合も同様に定義する。
見やすさのため、
- 二重超フィルターは$\mathbf{U},\mathbf{V},\mathbf{W}$
- 二重超フィルターの元は$\mathsf{A},\mathsf{B},\mathsf{C}$
- 超フィルターはこれまで通り$\mathcal{U},\mathcal{V},\mathcal{W}$
- 超フィルターの元はこれまで通り$A,B,C$
と、べき集合の階層ごとに使用するフォントと文字を固定します。
次に極限$\lim:\mathrm{Ult}^2(X)\rightarrow \mathrm{Ult}(X)$を定義します。
$X:$集合とする。
この時任意の$\mathbf{U}\in \mathrm{Ult}^2(X)$に対して
$\bigcup\limits_{\mathsf{A}\in\mathbf{U}}\bigcap\limits_{\mathcal{V}\in\mathsf{A}}\mathcal{V}(=\{B\subset X\ |\ ^{\exists}\mathsf{A}\in\mathbf{U}\ s.t.\ ^{\forall}\mathcal{V}\in\mathsf{A}\ ;\ B\in\mathcal{V}\})\in \mathrm{Ult}(X)$
が成り立つ。
この$\bigcup\limits_{\mathsf{A}\in\mathbf{U}}\bigcap\limits_{\mathcal{V}\in\mathsf{A}}\mathcal{V}$を$\lim \mathbf{U}$と書き$\mathbf{U}$の極限と呼ぶ。
$X:$集合$,\mathbf{U}\in \mathrm{Ult}^2(X)$とする。
$\lim\mathbf{U}$が命題3(1)-(4)を満たすことを示す。
- $\mathsf{A}\in\mathbf{U}$を任意に取る。
$\varnothing\notin\mathbf{U}$により$\mathsf{A}\neq\varnothing$なので、超フィルター$\mathcal{V}\in\mathsf{A}$が取れる。
この時$ \varnothing\notin\mathcal{V}$であるため$\varnothing\notin\lim\mathbf{U}$である。 - $\mathrm{Ult}(X)\in\mathbf{U}$である。
この時任意の$\mathcal{V}\in \mathrm{Ult}(X)$に対して$X\in\mathcal{V}$であるため$X\in\lim\mathbf{U}$である。 - $A,A'\in\lim\mathbf{U}$を任意に取る。
$\mathsf{B_0}\in\mathbf{U}$が存在して、任意の$\mathcal{V}\in\mathsf{B_0}$に対して$A'\in\mathcal{V}$となる。
$\mathsf{B'_0}\in\mathbf{U}$が存在して、任意の$\mathcal{V}\in\mathsf{B'_0}$に対して$A'\in\mathcal{V}$となる。
この時$\mathsf{B_0}\cap\mathsf{B'_0}\in\mathbf{U}$で、任意の$\mathcal{V}\in\mathsf{B_0}\cap\mathsf{B'_0}$に対して、$A,A'\in\mathcal{V}$より$A\cap A'\in\mathcal{V}$となる。
従って$A\cap A'\in\lim\mathbf{U}$である。 - $A,A'\subset X\ ,\ A\cup A'\in\lim\mathbf{U}$とする。
$\mathsf{B_0}\in\mathbf{U}$が存在して、任意の$\mathcal{V}\in\mathsf{B_0}$に対して$A\cup A'\in\mathcal{V}$となる。
この時任意の$\mathcal{V}\in\mathsf{B_0}$に対して$A\in\mathcal{V}$または$A' \in\mathcal{V}$であるから、
$\mathsf{C}=\{\mathcal{V}\in\mathsf{B_0}\ |\ A\in\mathcal{V}\},\mathsf{C'}=\{\mathcal{V}\in\mathsf{B_0}\ |\ A'\in\mathcal{V}\}$と定めれば、
$\mathsf{C}\cup\mathsf{C'}=\mathsf{B_0}\in\mathbf{U}$となるため$\mathsf{C}\in\mathbf{U}$または$\mathsf{C'}\in\mathbf{U}$である。
$\mathsf{C}\in\mathbf{U}$の場合、任意の$\mathcal{V}\in\mathsf{C}$に対して$A\in\mathcal{V}$となるため$A\in\lim\mathbf{U}$である。
同様にして$\mathsf{C'}\in\mathbf{U}$ならば$A'\in\lim\mathbf{U}$である。
以上により$\lim\mathbf{U}\in \mathrm{Ult}(X)$である。$\square$
この写像は78に於いて"compression operator"と呼ばれているものを超フィルターに制限したものです。また、910の"iterated limits of nets"の超フィルターに於ける対応物です。
"compression operator"がフィルター全体が成す順序集合上のネットに対する下極限であることから、本来であれば$\bigcup\limits_{\mathsf{A}\in\mathbf{U}}\bigcap\limits_{\mathcal{V}\in\mathsf{A}}\mathcal{V}$は「$\mathbf{U}$の下極限」と呼ぶべきですが、得られる値が超フィルター(すなわちフィルター全体が成す順序集合に於ける極大元)であることから「$\mathbf{U}$の極限」と呼んでいます。(そして実際に極限であることが本記事を通して示されます。)
$X:$集合に対して$\lim\circ \mathrm{Ult}(\langle\cdot\rangle_X)=id_{\mathrm{Ult}(X)}$が成り立つ。
$\mathcal{U}\in \mathrm{Ult}(X),A\in\lim \mathrm{Ult}(\langle\cdot\rangle_X)(\mathcal{U})$とする。
$\mathsf{B_0}\in \mathrm{Ult}(\langle\cdot\rangle_X)(\mathcal{U})$が存在して、任意の$\mathcal{V}\in\mathsf{B_0}$に対して$A\in\mathcal{V}$となる。
$\mathsf{B_0}\in \mathrm{Ult}(\langle\cdot\rangle_X)(\mathcal{U})\Leftrightarrow\langle\cdot\rangle_X^{-1}(\mathsf{B_0})\in\mathcal{U}$である。
$x\in\langle\cdot\rangle_X^{-1}(\mathsf{B_0})$とすると$\langle x\rangle_X\in\mathsf{B_0}$より$A\in\langle x\rangle_X\Leftrightarrow x\in A$となるため$\langle\cdot\rangle_X^{-1}(\mathsf{B_0})\subset A$である。
$\langle\cdot\rangle_X^{-1}(\mathsf{B_0})\in\mathcal{U}$と補題5により$A\in\mathcal{U}$である。
よって$\lim \mathrm{Ult}(\langle\cdot\rangle_X)(\mathcal{U})\subset\mathcal{U}$である。
超フィルターの極大性により$\lim \mathrm{Ult}(\langle\cdot\rangle_X)(\mathcal{U})=\mathcal{U}$である。
従って$\lim\circ \mathrm{Ult}(\langle\cdot\rangle_X)=id_{\mathrm{Ult}(X)}$である。$\square$
$X:$集合とすると$\lim\circ\langle\cdot\rangle_{\mathrm{Ult}(X)}=id_{\mathrm{Ult}(X)}$が成り立つ。
$\mathcal{U}\in \mathrm{Ult}(X),A\in\lim\langle\mathcal{U}\rangle_{\mathrm{Ult}(X)}$とする。
$\mathsf{B_0}\in\langle\mathcal{U}\rangle_{\mathrm{Ult}(X)}$が存在して、任意の$\mathcal{V}\in\mathsf{B_0}$に対して$A\in\mathcal{V}$となる。
$\mathsf{B_0}\in\langle\mathcal{U}\rangle_{\mathrm{Ult}(X)}\Leftrightarrow\mathcal{U}\in\mathcal{B_0}$であるため$A\in\mathcal{U}$である。
よって$\lim\langle\mathcal{U}\rangle_{\mathrm{Ult}(X)}\subset\mathcal{U}$である。
超フィルターの極大性により$\lim\langle\mathcal{U}\rangle_{\mathrm{Ult}(X)}=\mathcal{U}$である。
従って$\lim\circ\langle\cdot\rangle_{\mathrm{Ult}(X)}=id_{\mathrm{Ult}(X)}$である。$\square$
次の命題で見るように、$\mathrm{Ult}(f):\mathrm{Ult}(X)\rightarrow \mathrm{Ult}(Y)$は極限$\lim$に対して連続写像の様に振る舞います。
$X,Y:$集合$,f:X\rightarrow Y$に対して$\mathrm{Ult}(f)\circ\lim_X=\lim_Y\circ \mathrm{Ult}^2(f)$が成り立つ。
(ただし$\lim_X,\lim_Y$はそれぞれ$\mathrm{Ult}^2(X),\mathrm{Ult}^2(Y)$の極限)
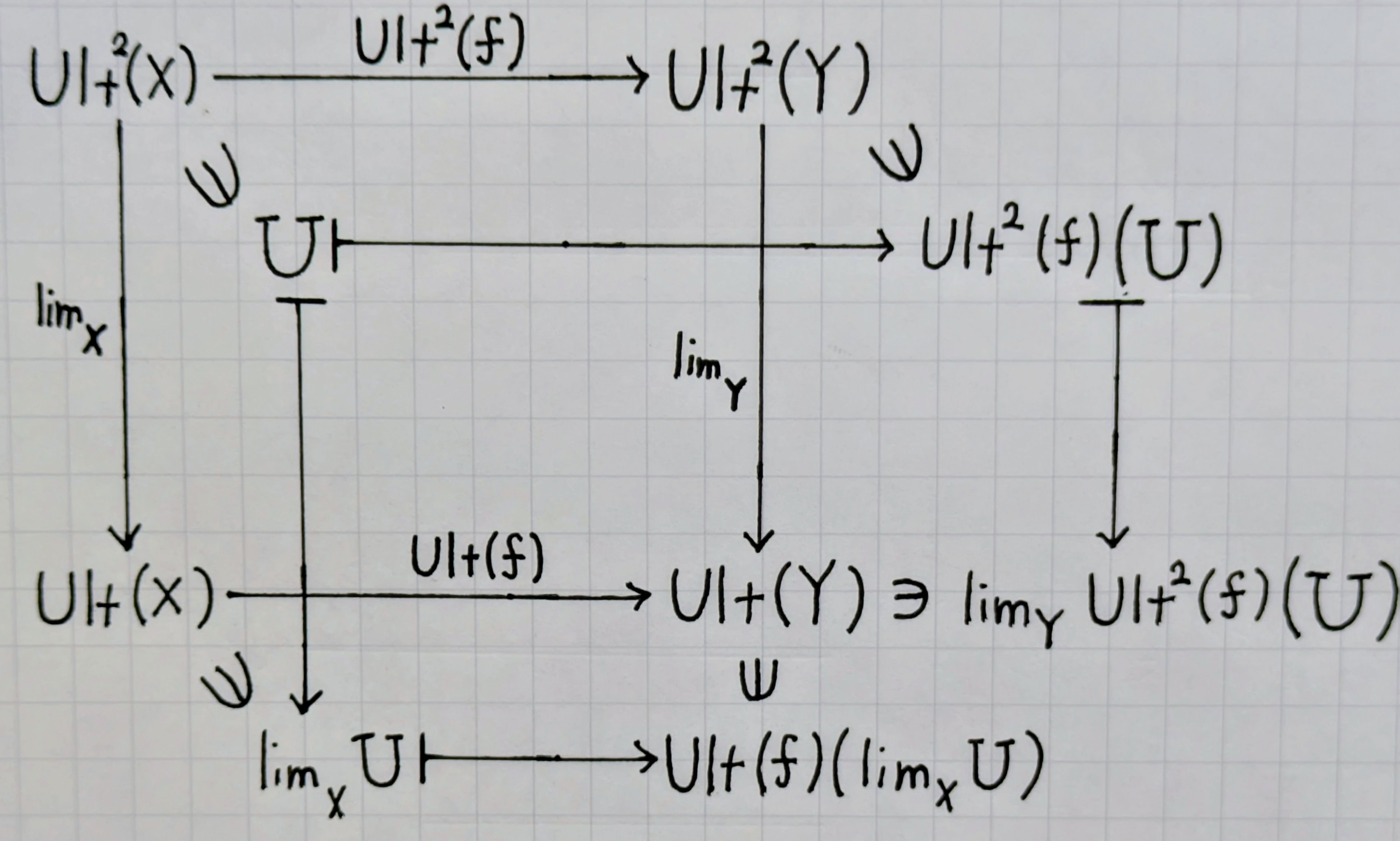 参考図
参考図
$\mathbf{U}\in \mathrm{Ult}^2(X)$を任意に取る。
$A\in \mathrm{Ult}(f)(\lim_X\mathbf{U})$とする。
$A\in \mathrm{Ult}(f)(\lim_X\mathbf{U})$より$f^{-1}(A)\in\lim_X\mathbf{U}$となるため、$\mathsf{B_0}\in\mathbf{U}$が存在して、任意の$\mathcal{V}\in\mathsf{B_0}$に対して$f^{-1}(A)\in\mathcal{V}$、すなわち$A\in \mathrm{Ult}(f)(\mathcal{V})$となる。
$\mathsf{B_0}\in\mathbf{U}$より$\mathrm{Ult}(f)(\mathsf{B_0})\in \mathrm{Ult}^2(f)(\mathbf{U})$である。
(ここで$\mathrm{Ult}(f)(\mathsf{B_0})$は写像$\mathrm{Ult}(f)$による$\mathsf{B_0}\subset \mathrm{Ult}(X)$の像である。)
$\mathcal{W}\in \mathrm{Ult}(f)(\mathsf{B_0})$を任意に取ると、$\mathcal{V}_\mathcal{W}\in \mathsf{B_0}$が存在して$\mathcal{W}=\mathrm{Ult}(f)(\mathcal{V}_\mathcal{W})\ni A$となる。
従って$A\in\lim_Y \mathrm{Ult}^2(f)(\mathbf{U})$となるため$\mathrm{Ult}(f)(\lim_X\mathbf{U})\subset\lim_Y \mathrm{Ult}^2(f)(\mathbf{U})$である。
超フィルターの極大性により$\mathrm{Ult}(f)(\lim_X\mathbf{U})=\lim_Y \mathrm{Ult}^2(f)(\mathbf{U})$である。
以上より任意の$\mathbf{U}\in \mathrm{Ult}^2(X)$に対して
$(\mathrm{Ult}(f)\circ\lim_X)(\mathbf{U})=(\lim_Y\circ \mathrm{Ult}^2(f))(\mathbf{U})$
が成り立つため$\mathrm{Ult}(f)\circ\lim_X=\lim_Y\circ \mathrm{Ult}^2(f)$である。$\square$
更に極限$\lim:\mathrm{Ult}^2(X)\rightarrow \mathrm{Ult}(X)$も、$\lim$自身に対して連続写像の様に振る舞います。
証明の流れは命題14と概ね同じです。
この命題でのみ
- 三重超フィルターは$\mathbf{U^{(3)}},\mathbf{V^{(3)}},\mathbf{W^{(3)}}$
- 三重超フィルターの元は$\mathsf{A^{(3)}},\mathsf{B^{(3)}},\mathsf{C^{(3)}}$
- $\mathrm{Ult}^3(X)$から$\mathrm{Ult}^2(X)$への極限は$\lim_{(2)}$
- 命題の対象となる極限は$\lim$
と記述します。その他はこれまで通りです。
$\lim$$\circ\lim_{(2)}=\lim\circ \mathrm{Ult}($$\lim$$)$が成り立つ。
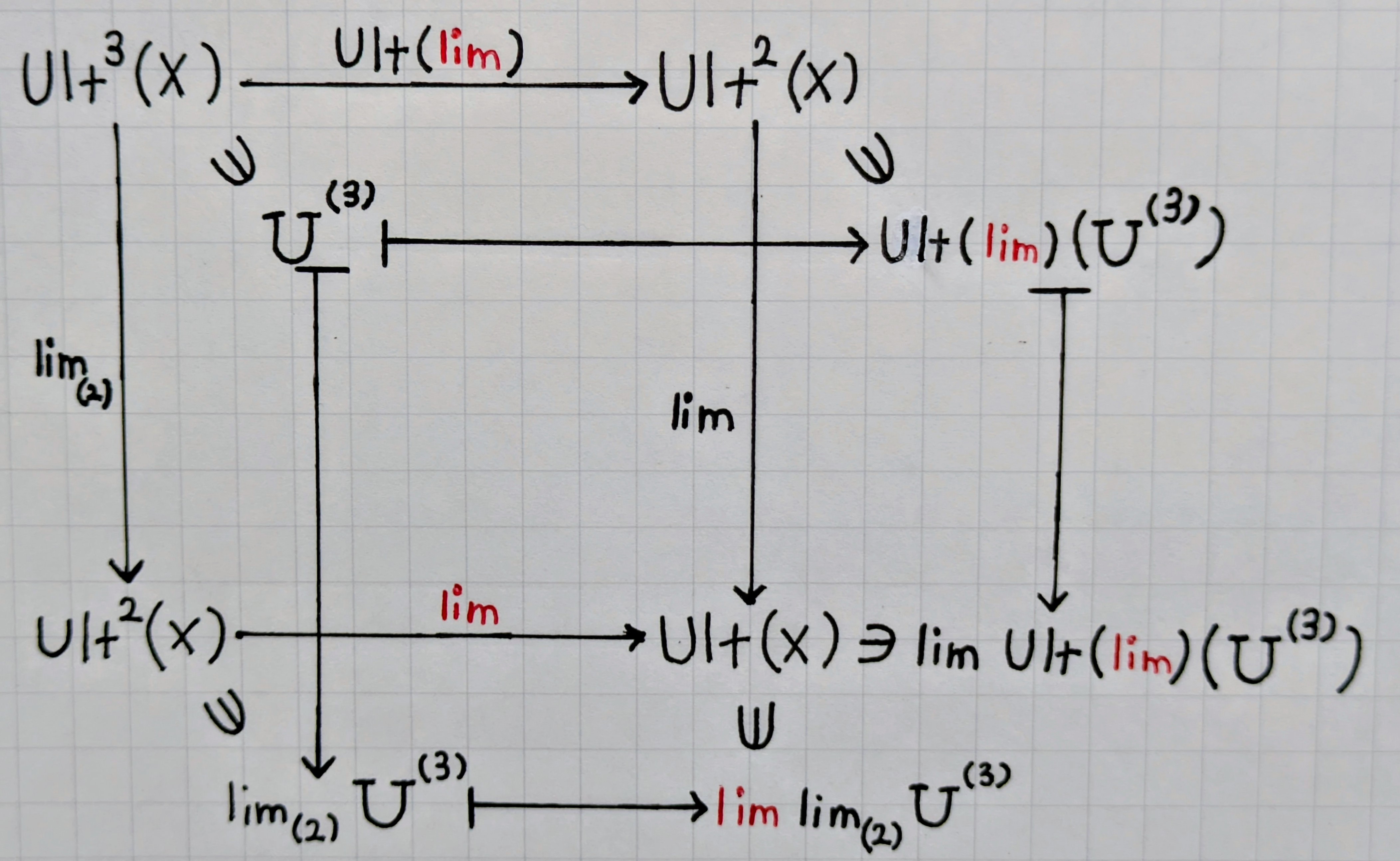 参考図
参考図
$X$を集合とし、$\mathbf{U^{(3)}}\in \mathrm{Ult}^3(X)$を任意に取る。
$A\in $$\lim$$\lim_{(2)}\mathbf{U^{(3)}}$とする。
$A\in $$\lim$$\lim_{(2)}\mathbf{U^{(3)}}$より$\mathsf{B_0}\in\lim_{(2)}\mathbf{U^{(3)}}$が存在して、任意の$\mathcal{V}\in\mathsf{B_0}$に対して$A\in\mathcal{V}$となる。
$\mathsf{B_0}\in\lim_{(2)}\mathbf{U^{(3)}}$より$\mathsf{C_0^{(3)}}\in\mathbf{U^{(3)}}$が存在して、任意の$\mathbf{W}\in\mathsf{C_0^{(3)}}$に対して$\mathsf{B_0}\in\mathbf{W}$となる。
$\mathsf{C_0^{(3)}}\in\mathbf{U^{(3)}}$より$\lim$$(\mathsf{C_0^{(3)}})\in \mathrm{Ult}($$\lim$$)(\mathbf{U^{(3)}})$である。
(ここで$\lim$$(\mathsf{C_0^{(3)}})$は写像$\lim$による$\mathsf{C_0^{(3)}}\subset \mathrm{Ult}^2(X)$の像である。)
$\mathcal{Z}\in$$\lim$$(\mathsf{C_0^{(3)}})$を任意に取る。
$\mathbf{W}_\mathcal{Z}\in\mathsf{C_0^{(3)}}$が存在して$\mathcal{Z}=$$\lim$$\mathbf{W}_\mathcal{Z}$となる。
この時$\mathsf{B_0}\in\mathbf{W}_\mathcal{Z}$で、任意の$\mathcal{V}\in\mathsf{B_0}$に対して$A\in\mathcal{V}$となるため、$A\in\lim\mathbf{W}_\mathcal{Z}=\mathcal{Z}$である。
従って$A\in\lim \mathrm{Ult}($$\lim$$)(\mathbf{U^{(3)}})$となるため
$\lim$$\lim_{(2)}\mathbf{U^{(3)}}\subset\lim \mathrm{Ult}($$\lim$$)(\mathbf{U^{(3)}})$である。
超フィルターの極大性により$\lim$$\lim_{(2)}\mathbf{U^{(3)}}=\lim \mathrm{Ult}($$\lim$$)(\mathbf{U^{(3)}})$である。
以上により任意の$\mathbf{U^{(3)}}\in \mathrm{Ult}^3(X)$に対して
$($$\lim$$\circ\lim_{(2)})(\mathbf{U^{(3)}})=(\lim\circ \mathrm{Ult}($$\lim$$))(\mathbf{U^{(3)}})$
が成り立つため$\lim$$\circ\lim_{(2)}=\lim\circ \mathrm{Ult}($$\lim$$)$である。$\square$
1章のまとめ
主な定義と命題の一覧は以下の通りです。
ここで$X,Y,Z$は集合$,f:X\rightarrow Y,g:Y\rightarrow Z$です。
定義
- $\mathcal{B}$を$X$の部分集合の空でない族とする。
$\mathcal{B}$が有限交叉族であるとは、任意の$A_1,A_2,\cdots,A_n\in\mathcal{B}$に対して$\bigcap\limits_{k=1}^nA_k\neq\varnothing$となることである。 - 超フィルターとは、包含関係について極大な有限交叉族のことである。
また、集合$X$の部分集合族$\mathcal{U}$が$X$の超フィルターであることは、単に以下の条件をすべて満たすこととしても定義できる。
①$\varnothing\notin\mathcal{U}$
②$X\in\mathcal{U}$
③$A,A'\in\mathcal{U}\Rightarrow A\cap A'\in\mathcal{U}$
④$A\cup A'\in\mathcal{U}\Rightarrow A\in\mathcal{U}$または$A'\in\mathcal{U}$
集合$X$の超フィルターの全体が成す集合を$\mathrm{Ult}(X)$と書く。 - $x\in X$に対し$\langle x \rangle_X=\{A\subset X\ |\ x\in A\}$と定め、これを$x$の固有フィルターと呼ぶ。
$\langle x \rangle_X\in\mathrm{Ult}(X)$である。 - $\mathcal{U}\in\mathrm{Ult}(X)$に対して$\mathrm{Ult}(f)(\mathcal{U})=\{B\subset Y\ |\ f^{-1}(B)\in\mathcal{U}\}$と定める。
$\mathrm{Ult}(f)(\mathcal{U})$を$\mathcal{U}$の$f$による像と呼ぶ。
$\mathrm{Ult}(f)(\mathcal{U})\in\mathrm{Ult}(Y)$である。 - $\mathbf{U}\in\mathrm{Ult}^2(X)$に対して$\lim \mathbf{U}=\bigcup\limits_{\mathsf{A}\in\mathbf{U}}\bigcap\limits_{\mathcal{V}\in\mathsf{A}}\mathcal{V}$と定める。
$B\subset X$に対して$B\in\lim\mathbf{U}\Leftrightarrow\mathsf{A}\in\mathbf{U}$が存在して、任意の$\mathcal{V}\in\mathsf{A}$に対して$B\in\mathcal{V}$である。
$\lim\mathbf{U}$を$\mathbf{U}$の極限と呼ぶ。
$\lim\mathbf{U}\in\mathrm{Ult}(X)$である。
命題
- 任意の有限交叉族$\mathcal{B}$に対して、$\mathcal{B}$を含む超フィルターが存在する。
- $\langle\cdot\rangle_X$は単射
- $\mathrm{Ult}$は写像について単射
- $\mathrm{Ult}(id_X)=id_{\mathrm{Ult}(X)}$
- $\mathrm{Ult}(g\circ f)=\mathrm{Ult}(g)\circ \mathrm{Ult}(f)$
- $\mathrm{Ult}(f)\circ\langle \cdot\rangle_X=\langle\cdot\rangle_Y\circ f$
- $\Im\mathrm{Ult}(f)=\{\mathcal{V}\in\mathrm{Ult}(Y)\ |\ \Im f\in\mathcal{V}\}$
特に$f:$全射$\Leftrightarrow\mathrm{Ult}(f):$全射 - $\mathrm{Ult}(f)\circ\lim=\lim\circ \mathrm{Ult}^2(f)$ ($\mathrm{Ult}(f)$の連続性)
- $\lim\circ \mathrm{Ult}(\langle\cdot\rangle_X)=\lim\circ\langle\cdot\rangle_{\mathrm{Ult}(X)}=id_{\mathrm{Ult}(X)}$ (自明な極限)
- $\lim\circ\lim=\lim\circ \mathrm{Ult}(\lim)$ ($\lim$の連続性)
2.超フィルターと位相空間
2-1.位相空間論の準備
本記事では閉包作用素・近傍系で位相空間を定義します。
辞書的に書き、定義の同値性は証明しません。このことについては3などをご参照ください。
$X:$集合とする。
$A\subset X$に対して$cl(A)\subset X$を対応させる操作が$X$の閉包作用素であるとは、以下の五条件を満たすことである。
(1) $cl(\varnothing)=\varnothing$
(2) 任意の$A\subset X$に対して$A\subset cl(A)$
(3) 任意の$A\subset X$に対して$cl(cl(A))\subset cl(A)$
(4) 任意の$A,B\subset{X}$に対して$A\subset B$ならば$cl(A)\subset cl(B)$
(5) 任意の$A,B\subset{X}$に対して$cl(A\cup B)\subset cl(A)\cup cl(B)$
集合$X$と$X$の閉包作用素$cl$の組$(X,cl)$を位相空間と呼ぶ。
また$(X,cl_X),(Y,cl_Y):$位相空間$,f:X\rightarrow Y$に対して、
$f$が連続写像$\stackrel{\mathrm{def}}{\Leftrightarrow}$任意の$A\subset X$に対して$f(cl_X(A))\subset cl_Y(f(A))$
で連続写像を定義する。
$X:$集合とする。
$x\in X$に対して$X$の部分集合の族$\mathcal{N}(x)$を対応させる操作が$X$の近傍系を定めるとは、以下の五条件を満たすことである。
(1) 任意の$x\in X$に対して$X\in\mathcal{N}(x)$
(2) 任意の$x\in X,\ A\in\mathcal{N}(x)$に対して$x\in A$
(3) 任意の$x\in X$と$A,B\in\mathcal{N}(x)$に対して$A\cap B\in\mathcal{N}(x)$
(4) 任意の$x\in X$と$B\subset X$に対して、$A\in\mathcal{N}(x)$が存在して$A\subset B$となるならば$B\in\mathcal{N}(x)$
(5) 任意の$x\in X,A\in\mathcal{N}(x)$に対して$B\subset A$が存在して、$x\in B$かつ任意の$y\in B$に対して$B\in\mathcal{N}(y)$
集合$X$と$X$の近傍系$\mathcal{N}$の組$(X,\mathcal{N})$を位相空間と呼ぶ。
また$(X,\mathcal{N}_X),(Y,\mathcal{N}_Y):$位相空間$,f:X\rightarrow Y$に対して、
$f$が連続写像$\stackrel{\mathrm{def}}{\Leftrightarrow}$任意の$x\in X,B\in\mathcal{N}_Y(f(x))$に対して$f^{-1}(B)\in\mathcal{N}_X(x)$
で連続写像を定義する。
$X:$集合$,cl:X$上の閉包作用素とする。
この時、$x\in X$に対して$\mathcal{N}(x)=\{A\subset X\ |\ x\notin cl(A^c)\}$と定めると、$\mathcal{N}$は$X$の近傍系を定める。
$X:$集合$,\mathcal{N}:X$上の近傍系とする。
この時、$A\subset X$に対して$cl(A)=\{x\in X\ |\ ^{\forall}B\in\mathcal{N}(x)\ ;\ A\cap B\neq\varnothing\}$と定めると、$cl$は$X$の閉包作用素である。
2-2.超フィルターの収束
この節では、位相空間上の超フィルターに対して収束を定義します。
また、超フィルターと閉方・近傍との関係、収束する超フィルターが持つ性質を示します。
$X:$位相空間$,\ x\in X,\ \mathcal{U}\in \mathrm{Ult}(X)$に対して、
$\mathcal{U}$が$x$に収束する$\stackrel{\mathrm{def}}{\Leftrightarrow}\mathcal{N}(x)\subset\mathcal{U}$
と定義する。
また$\mathcal{U}$が$x$に収束する事を$\mathcal{U}\rightarrow x$と書き、$\mathcal{U}$が$x$に収束しない事を$\mathcal{U}\nrightarrow x$と書く。
$(\mathbb{R},cl_\mathbb{R})$を通常の位相とすると、$\{(0,x)\subset\mathbb{R}\ |\ x>0\}$を含む超フィルター$\mathcal{U}\in \mathrm{Ult}(\mathbb{R})$に対して$\mathcal{U}\rightarrow 0$です。
この時$\mathcal{U}$は自由な超フィルターです。
【$\mathcal{U}\rightarrow 0$】
$A\in\mathcal{N}(0)$とする。
この時$x_0>0$が存在して$(-x_0,x_0)\subset A$となるが、
$(0,x_0)\subset A$となるため補題4により$A\in\mathcal{U}$
従って$\mathcal{U}\rightarrow 0$である。
【$\mathcal{U}$は自由な超フィルター】
$A\subset X$を補有限集合とする。
$x_0>0$が存在して$(0,x_0)\subset A$となるため補題4により$A\in\mathcal{U}$
従って$\mathcal{U}$は自由な超フィルターである。$\square$
次の補題で見るように、超フィルター$\mathcal{U}$が$x$に収束することは、$X$の部分集合が$x$に向かって小さくなっていくイメージで解釈できます。
$X:$位相空間$,\ x\in X,\ \mathcal{U}\in \mathrm{Ult}(X)$に対して、
$\mathcal{U}\rightarrow x\Leftrightarrow$任意の$A\in\mathcal{N}(x)$に対して$B\in\mathcal{U}$が存在して$B\subset A$
が成り立つ。
【$\mathcal{U}\rightarrow x\Rightarrow$任意の$A\in\mathcal{N}(x)$に対して$B\in\mathcal{U}$が存在して$B\subset A$】
$B=A$とすれば良い。
【$\mathcal{U}\rightarrow x\Leftarrow$任意の$A\in\mathcal{N}(x)$に対して$B\in\mathcal{U}$が存在して$B\subset A$】
$A\in\mathcal{N}(x),\ B\in\mathcal{U},\ B\subset A$とすると、
補題5により$A\in\mathcal{U}$となるため$\mathcal{N}(x)\subset\mathcal{U}$である。
従って$\mathcal{U}\rightarrow x$である。$\square$
超フィルターの収束を閉包作用素のみで書くと以下の様になります。
$X:$位相空間$,\ x\in X,\ \mathcal{U}\in \mathrm{Ult}(X)$に対して$\mathcal{U}\rightarrow x\Leftrightarrow x\in\bigcap\limits_{A\in\mathcal{U}}cl(A)$が成り立つ。
【$\mathcal{U}\rightarrow x\Rightarrow x\in\bigcap\limits_{A\in\mathcal{U}}cl(A)$】
$\mathcal{U}\rightarrow x,\ A\in\mathcal{U}$とする。
任意の$B\in\mathcal{N}(x)$に対して、$\mathcal{N}(x)\subset\mathcal{U}$により$B\in\mathcal{U}$であるから$A\cap B\neq\varnothing$である。
よって定義10により$x\in cl(A)$である。
従って$x\in\bigcap\limits_{A\in\mathcal{U}}cl(A)$である。
【$\mathcal{U}\rightarrow x\Leftarrow x\in\bigcap\limits_{A\in\mathcal{U}}cl(A)$】
対偶を示す。
$\mathcal{U}\nrightarrow x$とする。
$A_0\in\mathcal{N}(x)$が存在して$A_0\notin\mathcal{U}$となる。
補題4により$A_0^c\in\mathcal{U}$である。
$A_0\cap A_0^c=\varnothing$と定義10により$x\notin cl(A_0^c)$であるから$x\notin\bigcap\limits_{A\in\mathcal{U}}cl(A)$である。$\square$
当然成り立っていて欲しい性質として、固有フィルターは生成元に収束します。
$X:$位相空間$,x\in X$に対して$\langle x\rangle_X\rightarrow x$
任意の$A\in\mathcal{N}(x)$に対して$x\in A\Leftrightarrow A\in\langle x\rangle_X$となる。
従って$\mathcal{N}(x)\subset\langle x\rangle_X$より$\langle x\rangle_X\rightarrow x$である。$\square$
閉包を超フィルターで表すと以下の様になります。
$X:$位相空間$,\ x\in X,\ A\subset X$とする。
この時
$x\in cl(A)\Leftrightarrow\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$\mathcal{U}\rightarrow x$
が成立する。
【$x\in cl(A)\Rightarrow\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$\mathcal{U}\rightarrow x$】
$x\in cl(A)$とする。
定義8(3),定義10により$\mathcal{B}=\{A\cap B\ |\ B\in\mathcal{N}(x)\}$は有限交叉族であるから、命題1により$\mathcal{B}$を含む$\mathcal{U}\in \mathrm{Ult}(X)$が存在する。
定義8(1)により$A=A\cap X\in\mathcal{B}\subset\mathcal{U}$である。
任意の$B\in\mathcal{N}(x)$に対して$A\cap B\in\mathcal{U},A\cap B\subset B$と補題5により$B\in\mathcal{U}$であるから$\mathcal{N}(x)\subset\mathcal{U}\Leftrightarrow\mathcal{U}\rightarrow x$である。
【$x\in cl(A)\Leftarrow\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$\mathcal{U}\rightarrow x$】
$\mathcal{U}\in \mathrm{Ult}(X),A\in\mathcal{U}$かつ$\mathcal{U}\rightarrow x$とする。
この時任意の$B\in\mathcal{N}(x)$に対して$B\in\mathcal{U}$より$A\cap B\neq\varnothing$となるため、定義10により$x\in cl(A)$である。$\square$
同様に近傍系を超フィルターで表現すると以下の様になります。
$X:$位相空間$,\ x\in X$に対して$\mathcal{N}(x)=\bigcap\limits_{\mathcal{U}\rightarrow x}\mathcal{U}$
任意の$A\subset X$に対して
$A\in \mathcal{N}(x)\Leftrightarrow x\notin cl(A^c)(\because$定義9$)$
$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$A^c\in\mathcal{U}$ならば$\mathcal{U}\nrightarrow x(\because$命題19$)$
$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$\mathcal{U}\rightarrow x$ならば$A^c\notin\mathcal{U}$
$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$\mathcal{U}\rightarrow x$ならば$A\in\mathcal{U}(\because$補題4$)$
$\Leftrightarrow A\in\bigcap\limits_{\mathcal{U}\rightarrow x}\mathcal{U}$
となるため$\mathcal{N}(x)=\bigcap\limits_{\mathcal{U}\rightarrow x}\mathcal{U}$である。$\square$
超フィルターを用いて写像の連続性を特徴付けます。
距離空間に於ける極限を用いた連続写像の定義と全く同じ構図になっていることが見て取れます。
$X,Y:$位相空間$,\ f:X\rightarrow Y$とする。
この時
$f$が連続写像$\Leftrightarrow$任意の$x\in X,\ \mathcal{U}\in \mathrm{Ult}(X)$に対して$\mathcal{U}\rightarrow x$ならば$\mathrm{Ult}(f)(\mathcal{U})\rightarrow f(x)$
が成り立つ。
【$f$が連続写像$\Rightarrow$任意の$x\in X,\ \mathcal{U}\in \mathrm{Ult}(X)$に対して$\mathcal{U}\rightarrow x$ならば$\mathrm{Ult}(f)(\mathcal{U})\rightarrow f(x)$】
$f:$連続写像$,\ x\in X,\ \mathcal{U}\in \mathrm{Ult}(X),\ \mathcal{U}\rightarrow x$とする。
$B\in\mathcal{N}_Y(f(x))$を任意に取る。
$f$は連続なので$f^{-1}(B)\in\mathcal{N}_X(x)$である。
$\mathcal{U}\rightarrow x$より$\mathcal{N}_X(x)\subset \mathcal{U}$なので、$f^{-1}(B)\in\mathcal{U}$より$B\in \mathrm{Ult}(f)(\mathcal{U})$となる。
従って$\mathcal{N}_Y(f(x))\subset \mathrm{Ult}(f)(\mathcal{U})$より$\mathrm{Ult}(f)(\mathcal{U})\rightarrow f(x)$である。
【$f$が連続写像$\Leftarrow$任意の$x\in X,\ \mathcal{U}\in \mathrm{Ult}(X)$に対して$\mathcal{U}\rightarrow x$ならば$\mathrm{Ult}(f)(\mathcal{U})\rightarrow f(x)$】
$x\in X,\ B \in\mathcal{N}_Y(f(x))$とする。
$\mathcal{U}\rightarrow x$となる$\mathcal{U}\in \mathrm{Ult}(X)$を任意に取る。
仮定により$\mathrm{Ult}(f)(\mathcal{U})\rightarrow f(x)$となる。
定義11により$B\in \mathrm{Ult}(f)(\mathcal{U})$となるため$f^{-1}(B)\in\mathcal{U}$である。
$\mathcal{U}$の取り方と命題20により$f^{-1}(B)\in\mathcal{N}(x)$である。
従って$f$は連続写像である。$\square$
次の命題が記事全体の肝です。
収束する超フィルターと極限の組の全体$\{(\mathcal{U},x)\in \mathrm{Ult}(X)\times X\ |\ \mathcal{U}\rightarrow x\}$の極限に対する振る舞いについての命題です。
$X:$位相空間とする。
$\mathfrak{q}=\{(\mathcal{U},x)\in \mathrm{Ult}(X)\times X\ |\ \mathcal{U}\rightarrow x\}$と定め、
$\Pi:\mathfrak{q}\rightarrow \mathrm{Ult}(X):(\mathcal{U},x)\mapsto\mathcal{U}$
$\pi:\mathfrak{q}\rightarrow X:(\mathcal{U},x)\mapsto x$
を標準的な射影とする。
この時任意の$\mathbf{U}\in \mathrm{Ult}(\mathfrak{q})$と$x\in X$に対して、$\mathrm{Ult}(\pi)(\mathbf{U})\rightarrow x$ならば$\lim \mathrm{Ult}(\Pi)(\mathbf{U})\rightarrow x$が成り立つ。
$\mathbf{U}\in \mathrm{Ult}(\mathfrak{q}),\ x\in X,\ \mathrm{Ult}(\pi)(\mathbf{U})\rightarrow x$とする。
$A\in\mathcal{N}(x)$を任意に取る。
$B_0\subset A$が存在して、$x\in B_0$かつ任意の$y\in B_0$に対して$B_0\in\mathcal{N}(y)$となる。
$B_0\in\mathcal{N}(x)$と$\mathcal{N}(x)\subset \mathrm{Ult}(\pi)(\mathbf{U})$により$B_0\in \mathrm{Ult}(\pi)(\mathbf{U})\Leftrightarrow \pi^{-1}(B_0)\in\mathbf{U}$である。
よって$\Pi(\pi^{-1}(B_0))\in \mathrm{Ult}(\Pi)(\mathbf{U})$である。
$\mathcal{V}\in\Pi(\pi^{-1}(B_0))$を任意に取る。
$\Pi,\ \pi$の定義により$y_0\in B_0$が存在して$(\mathcal{V},y_0)\in\mathfrak{q}\Leftrightarrow\mathcal{N}(y_0)\subset\mathcal{V}$となる。
この時$B_0\in\mathcal{N}(y_0)\subset\mathcal{V},\ B_0\subset A$と補題5により$A\in\mathcal{V}$である。
従って$A\in\lim \mathrm{Ult}(\Pi)(\mathbf{U})$となるため$\mathcal{N}(x)\subset\lim \mathrm{Ult}(\Pi)(\mathbf{U})$となる。
以上により$\lim \mathrm{Ult}(\Pi)(\mathbf{U})\rightarrow x$である。$\square$
この命題は78の命題$\mathbf{K},\mathbf{F}$を超フィルターに制限したものです。また910の"iterated limitsの公理"の超フィルターに於ける対応物です。
2-3.超フィルターによる位相空間の特徴付け
収束する超フィルターとその極限の組の全体$\{(\mathcal{U},x)\in \mathrm{Ult}(X)\times X\ |\ \mathcal{U}\rightarrow x\}$は、位相空間の情報を全て持っています。つまり、超フィルターだけを用いて位相空間を定義することが可能です。
次の定理で見るように、命題18,21,22が超フィルターによる位相空間の特徴付けになっています。
$X:$集合とする。
$\mathfrak{q}\subset \mathrm{Ult}(X)\times X$とし、
$\Pi:\mathfrak{q}\rightarrow \mathrm{Ult}(X):(\mathcal{U},x)\mapsto\mathcal{U}$
$\pi:\mathfrak{q}\rightarrow X:(\mathcal{U},x)\mapsto x$
を標準的な射影とする。
$\mathfrak{q}$が以下の二条件を満たすとする。
- 任意の$x\in X$に対して$(\langle x\rangle_X,x)\in\mathfrak{q}$
- 任意の$\mathbf{U}\in \mathrm{Ult}(q)$と$x\in X$に対して$(\mathrm{Ult}(\pi)(\mathbf{U}),x)\in\mathfrak{q}$ならば$(\lim \mathrm{Ult}(\Pi)(\mathbf{U}),x)\in\mathfrak{q}$
この時、$X$上の位相が唯一つ存在して、
任意の$\mathcal{U}\in \mathrm{Ult}(X)$と$x\in X$に対して、$\mathcal{U}\rightarrow x\Leftrightarrow(\mathcal{U},x)\in\mathfrak{q}$
を満たす。
更に$(X,\mathfrak{q}_X),(Y,\mathfrak{q}_Y)$を(1),(2)を満たす構造$,\ f:X\rightarrow Y$とすると、
$(X,\mathfrak{q}_X),(Y,\mathfrak{q}_Y)$から定まる位相に対して、
$f$が連続$\Leftrightarrow$任意の$(\mathcal{U},x)\in\mathfrak{q}_X$に対して$(\mathrm{Ult}(f)(\mathcal{U}),f(x))\in\mathfrak{q}_Y$
が成立する。
$(X,\mathfrak{q})$を(1),(2)を満たす構造とする。
任意の$A\subset X$に対して
$cl(A)=\{x\in X\ |\ \mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$(\mathcal{U},x)\in\mathfrak{q}\}$
と定める。
$cl$が定義7(1)-(5)を満たすことを示す。
- 任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$\varnothing\notin\mathcal{U}$であるから$cl(\varnothing)=\varnothing$である。
- $A\subset X,\ x\in A$とすると$A\in\langle x\rangle_X,\ \ (\langle x\rangle_X,x)\in\mathfrak{q}$であるから$x\in cl(A)$である。
従って$A\subset cl(A)$である。 - $A\subset X,x\in cl(cl(A))$とする。
$\mathcal{U_0}\in \mathrm{Ult}(X)$が存在して$cl(A)\in\mathcal{U_0},\ (\mathcal{U_0},x)\in\mathfrak{q}$となる。
$B\in\mathcal{U_0}$に対して$\varphi(B)=\{(\mathcal{V},y)\in\mathfrak{q}\ |\ A\in\mathcal{V},\ y\in B\}\subset\mathfrak{q}$と定める。
任意の$B_1,B_2,\cdots ,B_n\in\mathcal{U_0}$に対して、
$y\in (\bigcap\limits_{k=1}^n B_k)\cap cl(A)$を取れば$\mathcal{V}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{V},\ (\mathcal{V},y)\in\mathfrak{q}$となるため、
$\bigcap\limits_{k=1}^n\varphi(B_k)=\varphi(\bigcap\limits_{k=1}^nB_k)\neq\varnothing$である。
従って$Im\ \varphi$は有限交叉族であるため、命題1により$Im\ \varphi$を含む$\mathbf{W_0}\in \mathrm{Ult}(\mathfrak{q})$が存在する。
$B\in\mathcal{U_0}$を任意に取る。
$\varphi(B)\subset\pi^{-1}(B),\ \varphi(B)\in\mathbf{W_0}$と補題5により$\pi^{-1}(B)\in\mathbf{W_0}$であるため$B\in \mathrm{Ult}(\pi)(\mathbf{W_0})$である。
よって$\mathcal{U_0}\subset \mathrm{Ult}(\pi)(\mathbf{W_0})$となるが、超フィルターの極大性により$\mathcal{U_0}=\mathrm{Ult}(\pi)(\mathbf{W_0})$である。
従って$(\mathrm{Ult}(\pi)(\mathbf{W_0}),x)=(\mathcal{U_0},x)\in\mathfrak{q}$となるため、仮定により$(\lim \mathrm{Ult}(\Pi)(\mathbf{W_0}),x)\in\mathfrak{q}$である。
$\varphi(X)\in\mathbf{W_0}$より$\Pi(\varphi(X))\in \mathrm{Ult}(\Pi)(\mathbf{W_0})$で、$\varphi$の定義により任意の$\mathcal{V}\in\Pi(\varphi(X))$に対して$A\in\mathcal{V}$となるため、$A\in\lim \mathrm{Ult}(\Pi)(\mathbf{W_0})$である。
$A\in\lim \mathrm{Ult}(\Pi)(\mathbf{W_0}),\ (\lim \mathrm{Ult}(\Pi)(\mathbf{W_0}),x)\in\mathfrak{q}$により$x\in cl(A)$である。
以上により$cl(cl(A))\subset cl(A)$である。 - $A,B\subset X,\ A\subset B$とする。
$x\in cl(A)$を任意に取ると、$\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U},\ (\mathcal{U},x)\in\mathfrak{q}$となる。
この時$B\in\mathcal{U}$であるから$x\in cl(B)$である。
従って$cl(A)\subset cl(B)$である。 - $A,B\subset X$とする。
$x\in cl(A\cup B)$を任意に取る。
$\mathcal{U_0}\in \mathrm{Ult}(X)$が存在して$A\cup B\in\mathcal{U_0},\ (\mathcal{U_0},x)\in\mathfrak{q}$となる。
この時$A\in\mathcal{U_0}$または$B\in\mathcal{U_0}$である。
$A\in\mathcal{U_0}$ならば$x\in cl(A)$($B$も同様)となるため$x\in cl(A)\cup cl(B)$である。
従って$cl(A\cup B)\subset cl(A)\cup cl(B)$である。
以上により$cl$は$X$の閉包作用素である。
この$cl$によりXに位相が定まる。$\square$
$x\in X,\ A\subset X,\ \mathcal{U}\in \mathrm{Ult}(X)$とする。
- 命題20と同様にして$\mathcal{N}(x)=\bigcap\limits_{(\mathcal{U},x)\in\mathfrak{q}}\mathcal{U}$が成り立つ。
- $\mathcal{U}\rightarrow x\stackrel{\mathrm{def}}{\Leftrightarrow}\mathcal{N}(x)\subset\mathcal{U}$と定める。
- この収束について、命題19により
$x\in cl(A)\Leftrightarrow\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$\mathcal{U}\rightarrow x$
が成り立つ。 - この収束について、命題20により$\mathcal{N}(x)=\bigcap\limits_{\mathcal{U}\rightarrow x}\mathcal{U}$が成り立つ。
まとめると、
- $x\in cl(A)$
$\Leftrightarrow\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$(\mathcal{U},x)\in\mathfrak{q}$
$\Leftrightarrow\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$\mathcal{U}\rightarrow x$ - $\mathcal{N}(x)=\bigcap\limits_{(\mathcal{U},x)\in\mathfrak{q}}\mathcal{U}=\bigcap\limits_{\mathcal{U}\rightarrow x}\mathcal{U}$
が成り立っている。
【$\mathcal{U}\rightarrow x\Rightarrow(\mathcal{U},x)\in\mathfrak{q}$】
$\mathcal{U}\rightarrow x$とする。
$A\in\mathcal{U}$に対して$\psi(A)=\{(\mathcal{V},x)\in\mathfrak{q}\ |\ A\in\mathcal{V}\}$と定める。
任意の$A_1,A_2,\cdots,A_n\in\mathcal{U}$に対して、$\bigcap\limits_{k=1}^nA_k\in\mathcal{U},\ \mathcal{U}\rightarrow x$により$x\in cl(\bigcap\limits_{k=1}^nA_k)$であるため、$\mathcal{V}\in \mathrm{Ult}(X)$が存在して$\bigcap\limits_{k=1}^nA_k\in\mathcal{V}$かつ$(\mathcal{V},x)\in\mathfrak{q}$となる。
この時$(\mathcal{V},x)\in\bigcap\limits_{k=1}^n\psi(A_k)$であるから$im\ \psi$は$\mathfrak{q}$の有限交叉族である。
従って命題1により$im\ \psi$を含む$\mathbf{W_0}\in \mathrm{Ult}(\mathfrak{q})$が存在する。
$A\in\mathcal{U}$を任意に取ると$\psi(A)\in\mathbf{W_0}$より$\Pi(\psi(A))\in\mathrm{Ult}(\Pi)(\mathbf{W_0})$で、$\Pi$の定義により任意の$\mathcal{V}\in\Pi(\psi(A))$に対して$A\in\mathcal{V}$が成り立つため$A\in\lim \mathrm{Ult}(\Pi)(\mathbf{W_0})$となる。
従って$\mathcal{U}\subset\lim \mathrm{Ult}(\Pi)(\mathbf{W_0})$となるが、超フィルターの極大性により$\mathcal{U}=\lim \mathrm{Ult}(\Pi)(\mathbf{W_0})$である。
$\pi^{-1}(\{x\})=\{(\mathcal{V},x)\in\mathfrak{q}\}=\psi(X)\in\mathbf{W_0}$より$\{x\}\in \mathrm{Ult}(\pi)(\mathbf{W_0})$となるため$\mathrm{Ult}(\pi)(\mathbf{W_0})=\langle x\rangle_X$である。
従って$(\mathrm{Ult}(\pi)(\mathbf{W_0}),x)=(\langle x\rangle_X,x)\in\mathfrak{q}$となるため$(\lim \mathrm{Ult}(\Pi)(\mathbf{W_0}),x)=(\mathcal{U},x)\in\mathfrak{q}$である。
【$\mathcal{U}\rightarrow x\Leftarrow(\mathcal{U},x)\in\mathfrak{q}$】
$(\mathcal{U},x)\in\mathfrak{q}$とすると$\mathcal{N}(x)=\bigcap\limits_{(\mathcal{V},x)\in\mathfrak{q}}\mathcal{V}\subset\mathcal{U}$となるため$\mathcal{U}\rightarrow x$である。$\square$
$cl'$を$X$の閉包作用素とし、$cl'$から定まる超フィルターの収束について$\mathcal{U}\rightarrow x\Leftrightarrow(\mathcal{U},x)\in\mathfrak{q}$が成り立つとする。
この時命題19により任意の$x\in X$と$A\subset X$に対して
$x\in cl'(A)$
$\Leftrightarrow\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$\mathcal{U}\rightarrow x$
$\Leftrightarrow\mathcal{U}\in \mathrm{Ult}(X)$が存在して$A\in\mathcal{U}$かつ$(\mathcal{U},x)\in\mathfrak{q}$
となる。よって示された。$\square$
$(X,\mathfrak{q}_X),(Y,\mathfrak{q}_Y)$を(1),(2)を満たす構造$,f:X\rightarrow Y$とする。
この時命題20により
$f$は連続写像
$\Leftrightarrow$任意の$x\in X,\ \mathcal{U}\in \mathrm{Ult}(X)$に対して$\mathcal{U}\rightarrow x$ならば$\mathrm{Ult}(f)(\mathcal{U})\rightarrow f(x)$
$\Leftrightarrow$任意の$(\mathcal{U},x)\in\mathfrak{q}_X$に対して$(\mathrm{Ult}(f)(\mathcal{U}),f(x))\in\mathfrak{q}_Y$
が成り立つ。$\square$
以上により定理23が示され、晴れて位相空間の同値な定義方法に超フィルターが仲間入りしました。
開集合・閉集合・内部についても超フィルターを用いて特徴付けを行っておきます。
$(X,\mathfrak{q}):$位相空間とする。この時以下が成立する。
(1) $A\subset X$が開集合$\Leftrightarrow$任意の$x\in A$と$\mathcal{U}\in \mathrm{Ult}(X)$に対して$(\mathcal{U},x)\in\mathfrak{q}$ならば$A\in\mathcal{U}$
(2) $A\subset X$が閉集合$\Leftrightarrow$任意の$x\in X$に対して、$\mathcal{U}\in \mathrm{Ult}(X)$が存在して$(\mathcal{U},x)\in\mathfrak{q}$かつ$A\in\mathcal{U}$となるならば$x\in A$
(3) $A\subset X$に対して$i(A)$を$A$の内部とする。
$x\in i(A)\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$(\mathcal{U},x)\in\mathfrak{q}$ならば$A\in\mathcal{U}$
(2)$A\subset X$とする。
$A$が閉集合$\Leftrightarrow cl(A)\subset A$
$\Leftrightarrow$任意の$x\in X$に対して$x\in cl(A)$ならば$x\in A$
$\Leftrightarrow$任意の$x\in X$に対して、$\mathcal{U}\in \mathrm{Ult}(X)$が存在して$(\mathcal{U},x)\in\mathfrak{q}$かつ$A\in\mathcal{U}$となるならば$x\in A$
(3)$x\in X,\ A\subset X$とする。
$x\in i(A)\Leftrightarrow A\in\mathcal{N}(x)\Leftrightarrow A\in\bigcap\limits_{(\mathcal{U},x)\in\mathfrak{q}}\mathcal{U}$
$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$(\mathcal{U},x)\in\mathfrak{q}$ならば$A\in\mathcal{U}$
(1)$A\subset X$とする。
$A$が開集合$\Leftrightarrow A\subset i(A)$
$\Leftrightarrow$任意の$x\in A$に対して$x\in i(A)$
$\Leftrightarrow$任意の$x\in A$と$\mathcal{U}\in \mathrm{Ult}(X)$に対して$(\mathcal{U},x)\in\mathfrak{q}$ならば$A\in\mathcal{U}\square$
2章のまとめ
超フィルターを用いた位相空間と位相的概念の定義は以下の様になります。
$X:$集合$,\ \mathfrak{q}\subset\ \mathrm{Ult}(X)\times X$とする。
$\Pi:\mathfrak{q}\rightarrow \mathrm{Ult}(X):(\mathcal{U},x)\mapsto\mathcal{U}$
$\pi:\mathfrak{q}\rightarrow X:(\mathcal{U},x)\mapsto x$
を標準的な射影とする。
この時$\mathfrak{q}$が$X$の位相を定めるのは、以下の二条件を満たす時である。
(1) 任意の$x\in X$に対して$(\langle x\rangle_X,x)\in\mathfrak{q}$
(2) 任意の$\mathbf{U}\in \mathrm{Ult}(\mathfrak{q})$と$x\in X$に対して$(\mathrm{Ult}(\pi)(\mathbf{U}),x)\in\mathfrak{q}$ならば$(\lim \mathrm{Ult}(\Pi)(\mathbf{U}),x)\in\mathfrak{q}$
また$(X,\mathfrak{q}_X),(Y,\mathfrak{q}_Y):$位相空間$,\ f:X\rightarrow Y$に対して
$f$が連続写像$\stackrel{\mathrm{def}}{\Leftrightarrow}$任意の$(\mathcal{U},x)\in\mathfrak{q}_X$に対して$(\mathrm{Ult}(f)(\mathcal{U}),f(x))\in\mathfrak{q}_Y$
で連続写像が定義される。
この定義の下、その他の位相的概念は以下の様に定まる。
$A\subset X$に対して
$A$が開集合$\Leftrightarrow^{\forall}x\in A,\ \mathcal{U}\in \mathrm{Ult}(X)\ ;\ (\mathcal{U},x)\in\mathfrak{q}\Rightarrow A\in\mathcal{U}$
$A$が閉集合$\Leftrightarrow^{\forall}x\in X\ ;\ ^{\exists}\mathcal{U}\in \mathrm{Ult}(X)\ s.t.\ (\mathcal{U},x)\in\mathfrak{q},\ A\in\mathcal{U}\Rightarrow x\in A$
$i(A)=\{x\in X\ |\ ^{\forall}\mathcal{U}\in \mathrm{Ult}(X)\ ;\ (\mathcal{U},x)\in\mathfrak{q}\Rightarrow A\in\mathcal{U}\}$
$cl(A)=\{x\in X\ |\ ^{\exists}\mathcal{U}\in \mathrm{Ult}(X)\ s.t.\ A\in\mathcal{U},\ (\mathcal{U},x)\in\mathfrak{q}\}$
で開集合・閉集合・内部・閉包が定まる。
$x\in X$に対して$\mathcal{N}(x)=\bigcap\limits_{(\mathcal{U},x)\in\mathfrak{q}}\mathcal{U}$で近傍系が定まる。
また$(\mathcal{U},x)\in\mathfrak{q}\Leftrightarrow\mathcal{N}(x)\subset\mathcal{U}\Leftrightarrow x\in\bigcap\limits_{A\in\mathcal{U}}cl(A)$である。
3.超フィルターとコンパクトハウスドルフ空間
以降、位相空間については開集合・閉集合・内部・閉包・近傍・超フィルターの収束の概念を自由に使います。
3-1.ハウスドルフ空間
$X:$位相空間に対して、
$X$はハウスドルフ
$\stackrel{\mathrm{def}}{\Leftrightarrow}$任意の異なる$x,y\in X$に対して、開集合$U,V\subset X$が存在して、$x\in U,\ y\in V,\ U\cap V=\varnothing$
と定義する。
ハウスドルフを超フィルターを用いて特徴付けると以下の様になります。
$X:$位相空間とする。
この時
$X$はハウスドルフ$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X),\ x,y\in X$に対して、$\mathcal{U}\rightarrow x$かつ$\mathcal{U}\rightarrow y$ならば$x=y$
が成り立つ。
【$X$はハウスドルフ$\Rightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X),\ x,y\in X$に対して、$\mathcal{U}\rightarrow x$かつ$\mathcal{U}\rightarrow y$ならば$x=y$】
$\mathcal{U}\in \mathrm{Ult}(X),\ x,y\in X,\ x\neq y$とする。
$X$はハウスドルフなので、開集合$V_x,V_y\subset X$が存在して、$x\in V_x,\ y\in V_y,\ V_x\cap V_y=\varnothing$となる。
$V_x\cap V_y=\varnothing$により$V_x\notin\mathcal{U}$または$V_y\notin\mathcal{U}$である。
$V_x\notin\mathcal{U}$の場合、$V_x\in\mathcal{N}(x)$であるから$\mathcal{U}\nrightarrow x$である。
同様に$V_y\notin\mathcal{U}$ならば$\mathcal{U}\nrightarrow y$である。
【$X$はハウスドルフ$\Leftarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X),\ x,y\in X$に対して、$\mathcal{U}\rightarrow x$かつ$\mathcal{U}\rightarrow y$ならば$x=y$】
対偶を示す。
$X$はハウスドルフでないとする。
相異なる$x,y\in X$が存在して、任意の開集合$U,V\subset X$に対して、$x\in U$かつ$y\in V$ならば$U\cap V\neq\varnothing$となる。
この時$\mathcal{N}(x)\cup\mathcal{N}(y)$は有限交叉族であるから、命題1により$\mathcal{W_0}\in \mathrm{Ult}(X)$が存在して$\mathcal{N}(x)\cup\mathcal{N}(y)$を含む。
この時$\mathcal{W_0}\rightarrow x,\ \mathcal{W_0}\rightarrow y$である。$\square$
3-2.コンパクト空間
$X:$位相空間とする。
この時
$X$はコンパクト$\stackrel{\mathrm{def}}{\Leftrightarrow}$任意の開集合の族$\mathcal{B}$に対して、$X=\bigcup\limits_{U\in\mathcal{B}}U$ならば$U_1,U_2,\cdots,U_n\in\mathcal{B}$が存在して$X=\bigcup\limits_{k=1}^nU_k$
と定義する。
$X:$位相空間とする。
この時
$X$はコンパクト$\Leftrightarrow$任意の閉集合のみからなる有限交叉族$\mathcal{B}$に対して$\bigcap\limits_{F\in\mathcal{B}}F\neq\varnothing$
が成り立つ。
【$X$はコンパクト$\Rightarrow$任意の閉集合のみからなる有限交叉族$\mathcal{B}$に対して$\bigcap\limits_{F\in\mathcal{B}}F\neq\varnothing$】
$\mathcal{B}$を閉集合のみからなる有限交叉族とする。
任意の$F_1,F_2,\cdots,F_n\in\mathcal{B}$に対して、$\mathcal{B}$は有限交叉族だから$\bigcup\limits_{k=1}^n(X\backslash F_k)=X\backslash(\bigcap\limits_{k=1}^nF_k)\subsetneq X$である。
よって任意の$F\in\mathcal{B}$に対して$X\backslash F$は開集合で、$X$はコンパクトだから$X\backslash(\bigcap\limits_{F\in\mathcal{U}}F)=\bigcup\limits_{F\in\mathcal{B}}(X\backslash F)\subsetneq X$である。
従って$\bigcap\limits_{F\in\mathcal{B}}F\neq\varnothing$である。
【$X$はコンパクト$\Leftarrow$任意の閉集合のみからなる有限交叉族$\mathcal{B}$に対して$\bigcap\limits_{F\in\mathcal{B}}F\neq\varnothing$】
$\mathcal{B}$を開集合の族,$\ X=\bigcup\limits_{U\in\mathcal{B}}U$とする。
この時$\{X\backslash U\ |\ U\in\mathcal{B}\}$は閉集合のみからなる集合族で$\bigcap\limits_{U\in\mathcal{B}} (X\backslash U)=X\backslash(\bigcup\limits_{U\in\mathcal{B}}U)=\varnothing$となるため、仮定により$\{X\backslash U\ |\ U\in\mathcal{B}\}$は有限交叉族ではない。
従って$U_1,U_2,\cdots,U_n\in\mathcal{B}$が存在して$X\backslash(\bigcup\limits_{k=1}^nU_k)=\bigcap\limits_{k=1}^n(X\backslash U_k)=\varnothing$となる。
この時$\bigcup\limits_{k=1}^nU_k=X$となるため、$X$はコンパクトである。$\square$
コンパクトを超フィルターを用いて特徴付けると以下の様になります。
$X:$位相空間とする。
この時
$X$はコンパクト$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$x\in X$が存在して$\mathcal{U}\rightarrow x$
が成り立つ。
【$X$はコンパクト$\Rightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$x\in X$が存在して$\mathcal{U}\rightarrow x$】
$\mathcal{U}\in \mathrm{Ult}(X)$とする。
補題25により$x\in\bigcap\limits_{A\in\mathcal{U}}cl(A)$が存在する。
この時命題17により$\mathcal{U}\rightarrow x$である。
【$X$はコンパクト$\Leftarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$x\in X$が存在して$\mathcal{U}\rightarrow x$】
$\mathcal{B}$を閉集合からなる$X$の有限交叉族とする。
命題1により$\mathcal{B}$を含む$\mathcal{U}\in \mathrm{Ult}(X)$が存在する。
仮定により$x\in X$が存在して$\mathcal{U}\rightarrow x$となる。
この時命題17により$x\in\bigcap\limits_{A\in\mathcal{U}}cl(A)\subset\bigcap\limits_{A\in\mathcal{B}}cl(A)=\bigcap\limits_{A\in\mathcal{B}}A$となるため$\bigcap\limits_{A\in\mathcal{B}}A\neq\varnothing$である。
従って命題26により$X$はコンパクトである。$\square$
3-3.コンパクトハウスドルフ空間
この節では、これまでの内容を位相空間論・圏論の言葉に翻訳していきます。
ただ換言するだけのものについては証明を付しません。
命題25,27により、位相空間がコンパクトハウスドルフ空間であることと、任意の超フィルターに対してただ一つの収束先が存在することは同値です。従って、コンパクトハウスドルフ空間の定義は次のように書くことができます。
$X:$集合、$\mathfrak{q}:\mathrm{Ult}(X)\rightarrow X$とする。
$(X,\mathfrak{q})$がコンパクトハウスドルフ空間であるとは、次の二条件を満たすことである。
(1) $\mathfrak{q}\circ\langle\cdot\rangle_X=id_X\ (\Leftrightarrow$任意の$x\in X$に対して$\mathfrak{q}(\langle x\rangle_X)=x\ )$
(2) $\mathfrak{q}\circ \mathrm{Ult}(\mathfrak{q})=\mathfrak{q}\circ\lim\ (\Leftrightarrow$任意の$\mathbf{U}\in \mathrm{Ult}^2(X)$に対して$\mathfrak{q}(\mathrm{Ult}(\mathfrak{q})(\mathbf{U}))=\mathfrak{q}(\lim\mathbf{U})\ )$
また、コンパクトハウスドルフ空間$(X,\mathfrak{q}_X),(Y,\mathfrak{q}_Y)$と写像$f:X\rightarrow Y$に対して、
$f$は連続写像$\Leftrightarrow f\circ\mathfrak{q}_X=\mathfrak{q}_Y\circ \mathrm{Ult}(f)$
$(\ \Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$f(\mathfrak{q}_X(\mathcal{U}))=\mathfrak{q}(\mathrm{Ult}(f)(\mathcal{U}))\ )$
と定義できる。
命題13,14,15は次の様に言い換えられます。
集合$X$に対して$(\mathrm{Ult}(X),\lim:\mathrm{Ult}^2(X)\rightarrow \mathrm{Ult}(X))$はコンパクトハウスドルフ空間である。
写像$f:X\rightarrow Y$に対して$\mathrm{Ult}(f):\mathrm{Ult}(X)\rightarrow \mathrm{Ult}(Y)$はコンパクトハウスドルフ空間間の連続写像である。
$\lim:\mathrm{Ult}^2(X)\rightarrow \mathrm{Ult}(X)$はコンパクトハウスドルフ空間間の連続写像である。
$Y$がコンパクトハウスドルフ空間の時、写像$X\rightarrow Y$と連続写像$\mathrm{Ult}(X)\rightarrow Y$の間には自然な全単射が存在します。
任意の集合$X,\ $コンパクトハウスドルフ空間$(Y,\mathfrak{q}_Y)$
写像$f:X\rightarrow Y,\ $連続写像$g:\mathrm{Ult}(X)\rightarrow Y$
に対して、
$\overline{f}=\mathfrak{q}_Y\circ \mathrm{Ult}(f):\mathrm{Ult}(X)\rightarrow Y:\mathcal{U}\mapsto\mathfrak{q}_Y(\mathrm{Ult}(f)(\mathcal{U}))$
$\overline{g}=g\circ\langle\cdot\rangle_X:X\rightarrow Y:x\mapsto g(\langle x\rangle_X)$
と定める。
$W,X:$集合$,\ (Y,\mathfrak{q}_Y),(Z,\mathfrak{q}_Z):$コンパクトハウスドルフ空間
写像$e:W\rightarrow X,\ f:X\rightarrow Y,\ $連続写像$g:\mathrm{Ult}(X)\rightarrow Y,\ h:Y\rightarrow Z$
を任意に取る。
この時、以下が成立する。
(1) $\overline{f}$は連続写像
(2) $\overline{\overline{f}}=f$
(3) $\overline{\overline{g}}=g$
(4) $\overline{f\circ e}=\overline{f}\circ \mathrm{Ult}(e)$
(5) $\overline{h\circ g}=h\circ\overline{g}$
これまでに証明したことを使えば等式の変形だけで示せる。
- $\overline{f}\circ\lim=\mathfrak{q}_Y\circ \mathrm{Ult}(f)\circ\lim=\mathfrak{q}_Y\circ\lim\circ \mathrm{Ult}^2(f)=\mathfrak{q}_Y\circ \mathrm{Ult}(\mathcal{q}_Y)\circ \mathrm{Ult}^2(f)=\mathfrak{q}_Y\circ \mathrm{Ult}(\mathcal{q}_Y\circ \mathrm{Ult}(f))=\mathfrak{q}_Y\circ \mathrm{Ult}(\overline{f})$
より$\overline{f}$は連続写像 - $\overline{\overline{f}}=\overline{f}\circ\langle\cdot\rangle_X=\mathfrak{q}_Y\circ \mathrm{Ult}(f)\circ\langle\cdot\rangle_X=\mathfrak{q}_Y\circ\langle\cdot\rangle_Y\circ f=id_Y\circ f=f$
- $\overline{\overline{g}}=\mathfrak{q}_Y\circ \mathrm{Ult}(\overline{g})=\mathfrak{q}_Y\circ \mathrm{Ult}(g\circ\langle\cdot\rangle_X)=\mathfrak{q}_Y\circ \mathrm{Ult}(g)\circ \mathrm{Ult}(\langle\cdot\rangle_X)=g\circ\lim\circ \mathrm{Ult}(\langle\cdot\rangle_X)=g\circ id_{\mathrm{Ult}(X)}=g$
- $\overline{f\circ e}=\mathfrak{q}_Y\circ \mathrm{Ult}(f\circ e)=\mathfrak{q}_Y\circ \mathrm{Ult}(f)\circ \mathrm{Ult}(e)=\overline{f}\circ \mathrm{Ult}(e)$
- $\overline{h\circ g}=h\circ g\circ\langle\cdot\rangle_X=h\circ\overline{g}\ \square$
命題8,9,10,28,29を圏の言葉に言い換えると次のようになります。
集合と写像の圏を$\mathbf{Set}$、コンパクトハウスドルフ空間と連続写像の圏を$\mathbf{KH}$と書く。
$\mathrm{Ult}:\mathbf{Set}\rightarrow\mathbf{KH}$は自由関手である。
3章のまとめ
3章の内容をまとめると以下の通りになります。
$X$を位相空間とすると、
- $X$はハウスドルフ$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X),\ x,y\in X$に対して、$\mathcal{U}\rightarrow x$かつ$\mathcal{U}\rightarrow y$ならば$x=y$
- $X$はコンパクト$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対して$x\in X$が存在して$\mathcal{U}\rightarrow x$
- $X$はコンパクトハウスドルフ$\Leftrightarrow$任意の$\mathcal{U}\in \mathrm{Ult}(X)$に対してただ一つの$x\in X$が存在して$\mathcal{U}\rightarrow x$
特に
- 集合$X$と写像$\mathfrak{q}:\mathrm{Ult}(X)\rightarrow X$に対して、
組$(X,\mathfrak{q})$がコンパクトハウスドルフ空間$\Leftrightarrow\mathfrak{q}\circ\langle\cdot\rangle_X=id_X$かつ$\mathfrak{q}\circ \mathrm{Ult}(\mathfrak{q})=\mathfrak{q}\circ\lim$ - コンパクトハウスドルフ空間$(X,\mathfrak{q}_X),(Y,\mathfrak{q}_Y)$と写像$f:X\rightarrow Y$に対して
$f$が連続写像$\Leftrightarrow f\circ\mathfrak{q}_X=\mathfrak{q}_Y\circ \mathrm{Ult}(f)$
が成り立ちます。
- 集合と写像の圏を$\mathbf{Set}$、
コンパクトハウスドルフ空間と連続写像の圏を$\mathbf{KH}$
とし、
$X,Y\in\mathbf{Set}$に対してXからYへの写像の全体を$\hom_{\mathbf{Set}}(X,Y)$
$X,Y\in\mathbf{KH}$に対してXからYへの連続写像の全体を$\hom_{\mathbf{KH}}(X,Y)$
とすると$\mathrm{Ult}:\mathbf{Set}\rightarrow\mathbf{KH}$は自由関手。
つまり以下の事柄がすべて成り立つ。
$X\in\mathbf{Set}$に対して$\mathrm{Ult}(X)\in\mathbf{KH}$
$f\in\hom_{\mathbf{Set}}(X,Y)$に対して$\mathrm{Ult}(f)\in\hom_{\mathbf{KH}}(\mathrm{Ult}(X),\mathrm{Ult}(Y))$
$\mathrm{Ult}(id_X)=id_{\mathrm{Ult}(X)}$
$\mathrm{Ult}(g\circ f)=\mathrm{Ult}(g)\circ \mathrm{Ult}(f)$
$X\in\mathbf{Set},\ Y\in\mathbf{KH}$に対して
$\hom_{\mathbf{Set}}(X,Y)\ni f\mapsto\overline{f}=\mathfrak{q}_Y\circ \mathrm{Ult}(f)\in\hom_{\mathbf{KH}}(\mathrm{Ult}(X),Y)$
$\hom_{\mathbf{KH}}(\mathrm{Ult}(X),Y)\ni g\mapsto\overline{g}=g\circ\langle\cdot\rangle_X\in\hom_{\mathbf{Set}}(X,Y)$
と定めるとこれらは互いに逆写像で、
$W,X\in\mathbf{Set},\ Y,Z\in\mathbf{KH}$
$W\stackrel{e}{\rightarrow}X\stackrel{f}{\rightarrow}Y\in\mathbf{Set},\ \mathrm{Ult}(X)\stackrel{g}{\rightarrow}Y\stackrel{h}{\rightarrow}Z\in\mathbf{KH}$
に対して、
$\overline{(W\stackrel{e}{\rightarrow}X\stackrel{f}{\rightarrow}Y)}=\mathrm{Ult}(W)\stackrel{\mathrm{Ult}(e)}{\longrightarrow}\mathrm{Ult}(X)\stackrel{\overline{f}}{\rightarrow}Y$
$\overline{(\mathrm{Ult}(X)\stackrel{g}{\rightarrow}Y\stackrel{h}{\rightarrow}Z)}=X\stackrel{\overline{g}}{\rightarrow}Y\stackrel{h}{\rightarrow}Z$
が成り立つ。
あとがき
結構長い間「位相空間って結局何なんだ・・・」と思って文献を漁っていたので、あらかた納得できる形にまとめられて良かったです。
個人的には位相空間の定義から「集合論だけで語れるもの」と「当然の要請」を限界まで取り去った残り、つまり「位相空間を位相空間たらしめている条件」が定理23の(2)だと考えています。
また収束を用いて位相空間を定義する上で、最小限の要素として超フィルターを用いるのは個人的に必須でした。収束を用いた位相空間の定義にはフィルターやネットを用いたものが知られていますが、こと位相空間を定義するに当たっては、フィルターについては包含関係が無駄に見え、ネットに至っては収束するネットの全体は大きすぎて集合にすらならないという状況だったからです。(収束空間の様な超弱い空間の定義には使えますが・・・)
自由関手$\mathbf{Set}\rightarrow\mathbf{KH}$の存在は『圏論の基礎』にも書かれています。結果的に1,3章はその関手と関手から定まるモナドを書き下しただけに過ぎませんが、その関手とモナドを書き下す記述も、位相の定義に結び付ける記述も見つけられなかったので、この記事を書く意味はあったのかなと思います。
余談ですが、一般化シンドロームの名にふさわしい記事に仕上がったのが嬉しいです。なお超フィルターの定義が極大なフィルターではなく極大な有限交叉族であったり、閉包作用素の定義がやたらと細かく分割されてたりするのが一般化シンドロームの主な症状です。
以上です。高評価やコメントをしていただけましたら大変嬉しいです。