超伝導体におけるvortex解

はじめに

最近LK-99という常温常圧超伝導体の候補が話題になりました。ネット上で大きな盛り上がりを見せ、関連株の上昇も起こったほどなのですが、他グループによる検証結果は尽く否定的ですLK-99。

LK-99が常温・常圧下で磁石に浮く動画がいくつか違うグループから公開されています。超伝導体が磁石の上に安定して浮く現象は、マイスナー効果と「ピン留め効果」の結果であることはよく知られています。一方LK-99の動画を見ると、完全には浮いておらず、一部は必ず接地しているように見受けられます。よって反発力は働くが安定はしておらず、少なくともピン留めは起こっていないようです。（※ピン留めにも見える"LK-99"の浮上動画も1つだけありますが、果たして...）

磁束の侵入・常伝導スポットとピン留め効果

このピン留め効果とはなんでしょうかMurakami1993。

大前提として、超伝導体は、その状況下で常伝導よりも超伝導であるほうがエネルギーが低いために超伝導状態になっています。

超伝導体を磁場の下に置きます。マイスナー効果により超伝導体は磁場を排斥しますが、排斥するにもエネルギーコストがかかるので、ある程度大きな磁場にさらされると常伝導になります。第1種超伝導体(Type I)は、臨界磁場に達すると全体が完全に常伝導になります（図1上右）。一方第2種超伝導体(Type II)には下部臨界磁場というものが存在します。これを超えると磁場の一部が超伝導体内に紐状・渦状で侵入し、侵入した部分だけ常伝導になります（図1下右）。そしてそれ以外の部分は超伝導を保ちます。これによりType IIは比較的強い磁場でも安定してバルクとしての超伝導状態を保ちます。

Type IとIIの違い。Type Iは臨界磁場を超えると全体が常伝導体になる。Type IIは下部臨界磁場を超えると、磁場が侵入した部分のみが常伝導体となり（青い部分）、それ以外の部分は超伝導体（オレンジ色の部分）を保つ。

ところがType IIに電流を流すと、磁束と電流の間にローレンツ力が働き動いてしまいます。これは電流に対する抵抗となって現れ、せっかくのマイスナー効果よる抵抗ゼロの性質が破れてしまいます。

ここでType IIに常伝導のスポットが点々と存在しているとします。磁場が侵入した部分は常伝導になり、超伝導よりもエネルギーの高い状態になります。それなら磁場はなるべく常伝導のスポットを通ったほうが全体のエネルギーが低くなります。これにより、磁束線は常伝導スポットに「ピン留め」され、電流を流しても磁束は動かず抵抗ゼロの状態が保たれます。

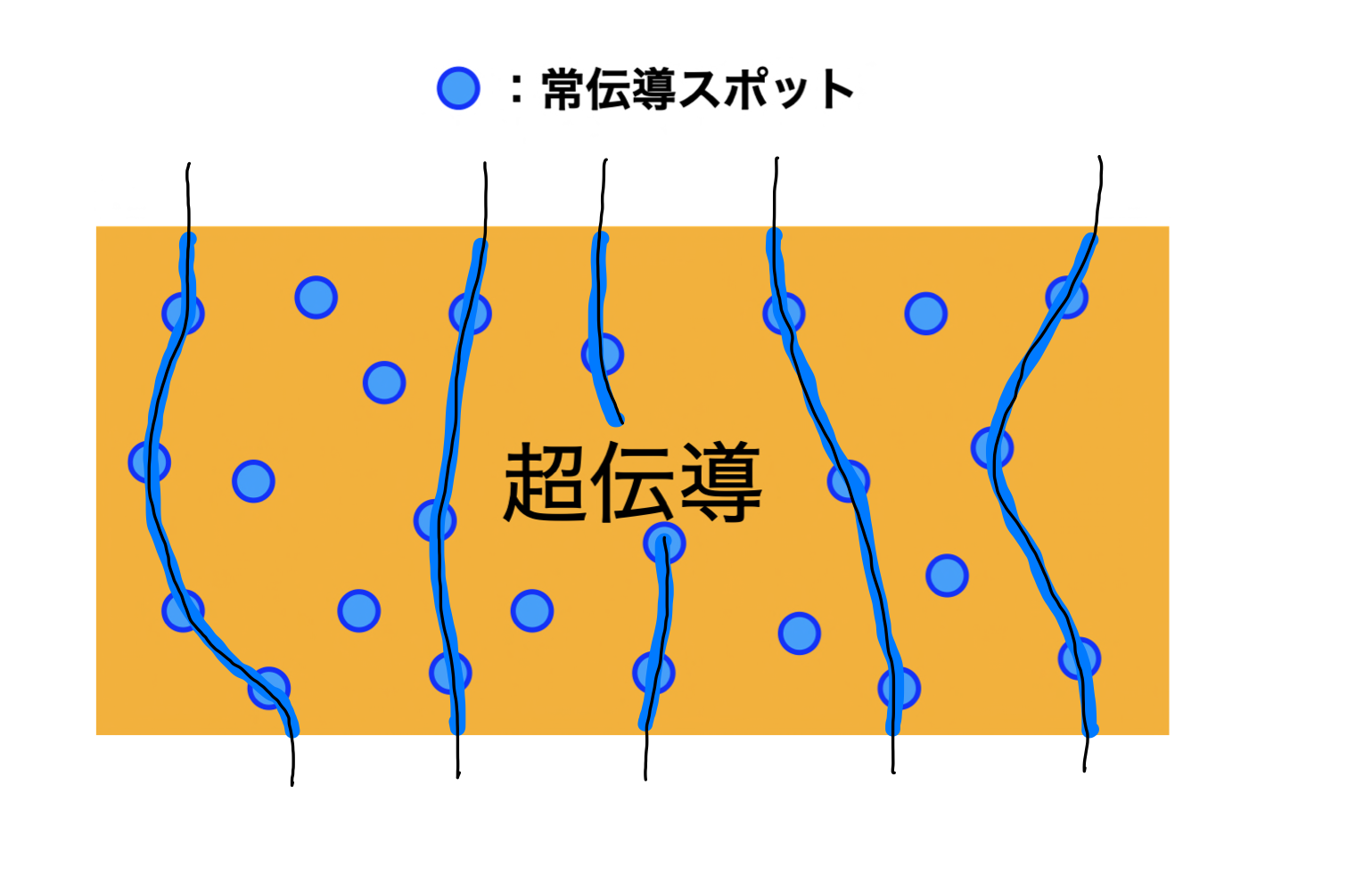ピン留めの概念図。青い部分は常伝導状態。エネルギーを下げるため、磁束（黒い線）は常伝導スポットを通る。

さらにはこの効果により、超伝導体が磁石に反発しても安定的に浮くことができます（注1）。

本記事の内容：Nielsen-Olesen vortexの導出

本記事では、超伝導体内に侵入しする磁束のモデルであるNielesen-Olesen vortexに関して説明します。（※ピン留めには言及しません）

Type IIに磁場が侵入する機構は、Ginzburg-Landau理論に電磁場を結合させた理論により記述できます。これは"Higgs場"にU(1)ゲージ場が結合する、Abelian-Higgs模型と呼ばれる系に等価です。この系には渦状の解が存在し、Nielsen-Olesen vortexと呼ばれます。この解に関する位相の条件から、磁束の量子化が示せます。

これは第2種超伝導体内に磁場が渦として侵入し、またその磁束が量子化されることのモデルとなっています。

本記事はRefs.Kondo2005Nastase2019Shifman2022を参考にしています。

Abelian-Higgs模型

Ginzburg-Landau理論（GL理論）というものがあります。この理論では、系の対称性が自発的に破れているとき、系の自由エネルギー等を対称性の破れのオーダーパラメータのべきで記述します。そして破れが小さいとしてその低次の項のみを取り出し解析します。非常に広範に適用できる理論・考え方です。物性物理・素粒子物理・宇宙論等様々な分野で有用です。

これから考える系はAbelian Higgs模型（AH模型）と言われる以下のような系です：

この模型はU(1)ゲージ場$A_\mu$にスカラー場$\phi$が結合している系です。これはGL理論とみなすことができ、その場合$\phi$がオーダーパラメータに対応します。超伝導の場合$\phi$はU(1)対称性の自発的破れのオーダーパラメータである、電子のCooper対の期待値に対応します。Higgsの名前が冠されているのは、$\phi$がHiggs場と同様の役割を果たすからです。

でもとりあえず物理的なことは忘れ、この系の解を探します。

Abelian-Higgs模型におけるvortex

AH模型における渦状の解、vortex解に関して考察します。

運動方程式と軸対称なAnsatz

Euler-Lagrange方程式
\begin{align} \begin{cases} \displaystyle\partial_\mu \frac{\partial {\cal L}}{\partial(\partial_\mu\phi)} -\frac{\partial{\cal L}}{\partial\phi}=0,\\ \displaystyle\partial_\mu \frac{\partial {\cal L}}{\partial(\partial_\mu A^\nu)} -\frac{\partial{\cal L}}{\partial A^\nu}=0 \end{cases} \end{align}
に上記Langangianを代入して計算すると以下のようになります：
\begin{align} \begin{cases} D^\mu D_\mu \phi=-2\lambda\phi(|\phi|^2-\phi_0^2) \ \ \ \ \ (\phi^2_0:=\mu^2/\lambda)\\ \displaystyle \partial^\nu F_{\mu\nu}=J_\mu, \ \ \ J_\mu:= \frac{1}{2}iq(\phi^*\partial_\mu\phi -\phi\partial_\mu \phi^*) +q^2A_\mu |\phi|^2 \end{cases} \end{align}
$J_\mu$はカレントです。以下静的な渦状の解を求めることにして、$t$依存性は考えません。

渦は軸対称なので$z$軸対称かつ$x\text{-}y$平面の円対称解を考えます。そのため円柱座標$(\rho,\varphi,z)$に移ります（$\rho=\sqrt{x^2+y^2}, \varphi=\tan^{-1}(y/x)$）。次のようなansatzをおきます：
\begin{align} \begin{cases} {\bf A}={\bf e}_\varphi A(\rho),\\ \phi=f(\rho)e^{in\varphi} \end{cases} \end{align}
すなわちゲージ場は${\bf e}_\varphi$方向の成分のみを持ちかつ$\rho$にのみ依存。$\phi$は$\rho$依存性の他に$\varphi$に関する位相をもつとします。また$n$は、$\varphi\to\varphi+2\pi$に対する$\phi$の一価性より整数です。

EoMを円柱座標で書き直し、上記のansatzを代入すると以下を得ます：
\begin{align} &\text{EoM for }\phi: -\left(\frac{\partial^2}{\partial\rho^2}+\frac{1}{\rho}\frac{\partial}{\partial\rho} \right)f +\left(\frac{n}{\rho}-qA\right)^2f +2\lambda\left( f^2-\phi_0^2 \right)f=0,\\ &\text{EoM for }A_\mu: \frac{\partial}{\partial\rho}\left[\frac{1}{\rho} \frac{\partial}{\partial\rho}(\rho A)\right] +\left(\frac{qn}{\rho}-q^2A\right)f^2=0 \tag{1} \end{align}

境界条件

$\rho$が大きい領域での解の振る舞いに関して考えます。この領域で解はエネルギー最小の状態＝真空に近づかなければいけません。$f$に関しては$\phi$が$V$を最小にする条件から
\begin{align} f(\varphi\to \infty)\to \phi_0 \end{align}
になります。一方$A_\mu$に関してはゼロなら電場も磁場もゼロでありエネルギー最小です。しかし実際には$A_\mu=0$は強すぎる条件であり、$A_\mu=0$とゲージ同値であるpure gauge form
\begin{align} \frac{1}{q}\partial_\mu \chi \tag{2} \end{align}
に近づけば電磁場はゼロになります。ここで$\chi=n\varphi$とすると、${\boldsymbol \partial}:=(\partial/\partial x,\partial/\partial y)$、${\bf e}_\varphi$を $\varphi$方向の基底として
\begin{align} \frac{1}{q}{\boldsymbol \partial}\chi=\frac{n}{q\rho}{\bf e}_\varphi \end{align}
であるから、このとき
\begin{align} A=\frac{n}{q\rho} \tag{3} \end{align}
となります。よってこの$A$はpure gauge formでありエネルギーを最小にします。そしてEq.(1)をみると
\begin{align} A=\frac{n}{q\rho}, \ \ \ f=\phi_0 \tag{4} \end{align}
はEoMの解となっています。よってEq.(4)はエネルギー最小のEoMの解、すなわち真空解です。

さらに$e^{in\varphi}$は原点でsingularなので、$f(r=0)=0$を課すことで解を原点でもなめらかにします。

磁束の量子化

ある局面$S$を貫く磁束$\Phi$を計算します。$dS^{\mu\nu}$を$\mu,\nu$方向の微小面積要素とします。するとStokesの定理より
\begin{align} \Phi=\int_S F_{\mu\nu} dS^{\mu\nu}=\oint_{\partial S} A_\mu dx^\mu \end{align}
のように$\Phi$をゲージ場の線積分で書くことができます。$A$の$\rho$の小さい領域での振る舞いはわかりませんが、$S$を$\rho$が十分大きいところにとれば、$\Phi$を真空解で評価できます。$\partial S$の経路を${\bf e}_\rho,{\bf e}_z$に直交するように$z={\rm const.}$の円にします。すると
\begin{align} \Phi &= \oint_{\partial S} A_\mu dx^\mu =\oint_{\partial S} \frac{1}{q}\partial_\mu \chi dx^\mu\\ &=\frac{1}{q}[\chi(\varphi)]_0^{2\pi}=\frac{1}{q}[n\varphi]_0^{2\pi}\\&=\frac{2\pi n}{q} \end{align}
を得ます。$\phi$の$2\pi$回転に対する一価性から$n$は整数なので、これは磁束が量子化されていることを示します。これはトポロジカルな不変量です。

BPS limit

Eq.(1)の解を一般的に解析的に求めることは無理なのですが、BPS limitと呼ばれる極限では運動方程式が簡単になります。またこの極限は、AH系に限らず物理的に重要なことが多いです。そこでここではBPS limitにおいて運動方程式を導き、数値的に解を計算します。

そのために系のエネルギーを計算しておきます。$z$方向には並進不変性があるので、ここでは改めて空間2次元の場合を考えます。静的な配位を考え場は時間に依存しないとして時間微分は落とし、また後に上記の場のansatzを入れることを考慮し$A_0$はゼロとします。すると
\begin{align} E=\int d^2x \left(\frac{1}{2}{F_{12}}^2+\frac{1}{2}|D_k\phi|^2+V(\phi)\right) \end{align}
ここで$F_{12}$は磁場に相当します：$B=F_{12}$。考察対象の2次元空間は、3次元中の2次元だと考え、磁場は$z$方向を向いているとします。

これを変形し「平方完成」すると以下のようになります（Bogomol'nyi completionと呼ばれます）
\begin{align} E=\int d^2x \left\{ |(D_1+iD_2)\phi|^2+[F_{12}+q(|\phi|^2-\phi_0^2)]^2\right\}\\ +2\pi n\phi_0^2+\frac{\lambda-q^2}{2} \int d^2x(|\phi|^2-\phi_0^2)^2 \end{align}
$2\pi n\phi_0^2$は量子化された磁束に関する項であり、$n$は整数です。この式から$\lambda\ge q^2$ならば、エネルギーに関して下限が存在します：
\begin{align} E\ge 2\pi n\phi_0^2 \end{align}
このようなエネルギーの下限をBogomol'nyi boundと呼びます。

ここで
\begin{align} \lambda=q^2 \end{align}
の場合を考えます。このとき最後の項は消え、エネルギーは上記の下限を実現し得ます。エネルギーの下限を実現することを「Bogomol'nyi boundをsaturateする」と言い、このときEoMを満たす解はBPS解と呼ばれます。

BPS解を求めます。このとき第1項・第2項がゼロになるので
\begin{align} \begin{cases} |(D_1+iD_2)\phi|^2=0,\\ F_{12}+e(|\phi|^2-\phi_0^2)=0 \end{cases} \end{align}
が成立します。極座標に移り($(x,y)\to(\rho,\varphi)$)、前章の解のansatzを代入すると
\begin{align} &A=\frac{1}{q} \left( \frac{n}{\rho}-\frac{f'}{f} \right)\\ & f''=\frac{f'^2}{f}-\frac{f'}{f\rho}+q^2(f^2-\phi_0^2) \end{align}
を得ます。$f'$は$\rho$微分です。上の式において$A$は$f,f'$で書かれており、下の方程式は$f$のみで構成されています。下の方程式を解いて$f$を求め、その解を上の方程式に入れば$A$が求まります。前述したように、$f(r\to 0)=0$と$f(r\to \infty)=\phi_0$が境界条件です。

数値計算と解に関する考察

数値的にこれを解き、プロットしたのが図3です。

BPS limitでの$\phi$の振幅$f$と磁場$B$。パラメータは$\lambda=q^2=\phi_0=1$にしている。

磁場$B$は$\rho$が小さい範囲のみで存在しており、紐状に絞られていることがわかります。逆に"Higgs場"$\phi$の値はこの領域で小さく、$\rho$が大きい領域で$\phi_0=1$に近づきます。

ここでAH系の対称性について述べておきます。AH系のLagrangianはU(1)のゲージ変換
\begin{align} A_\mu\to A_\mu +\frac{1}{q}\partial_\mu \chi(x), \ \ \ \phi\to e^{i\chi(x)}\phi(x) \end{align}
に関して不変です。しかし$\rho$が大きいところでHiggs場が真空の配位に近づくと、量子論的には$\phi$からその真空での値$\phi_0$を差し引いて、ポテンシャル$V$の最小の場所の周りで場を展開しなおさないといけません。よって新たに$\tilde\phi:=\phi-\phi_0$という場を導入します。このとき$\tilde\phi$と$A_\mu$の結合項により、$\tilde\phi$で書かれたLagrangianにおいて、ゲージ場に質量項が生じ、上記のU(1)対称性が破れます。そしてゲージ場が質量を持つことで磁場が排斥される真空が実現します。これがマイスナー効果に対応します（注2）。対称性が破れている相をHiggs phase、回復している相をCoulomb phaseと呼びます。このようなメカニズムをHiggs機構と呼びます。

詳しいことは省略しますが、磁場$B$が減少する場所は、Higgs機構で生じたゲージ場の質量の逆$m_V^{-1}=1/(\sqrt{2}q\phi_0)$付近ですShifman2022。一方Higgs場$\phi$が増大するのは、Higgs場の質量の逆$m_H^{-1}=1/(\sqrt{2\lambda}\phi_0)$付近です。これらの値はBPS limit:$\lambda=q^2 $で等しくなります。図3で用いたパラメータでは、これらはどちらも$1/\sqrt{2}$になります。そして実際数値計算を見るとその付近で$B,f$は共に減少・増大しています。

複数のvortexの相互作用は$m_V, m_H$の大小で定まります:

• $m_V>m_H$: vortex間の相互作用は引力。超伝導体で言えばtype Iに相当する。複数のvortexは安定には存在できない。
• $m_V< m_H$: vortex間の相互作用は斥力。type IIに相当。複数のvortexが安定して存在。
• $m_V=m_H$: BPS limit。vortex間には相互作用が働かない。これはBogomol'nyi boundをsaturateしていることによる。

type IIの場合、vortexはその斥力により格子を形成します。これはAbrikosov latticeと呼ばれます。

ただしAH系は相対論的不変性を持つので、その点は実際の超伝導とは異なります。実際の超伝導体のような非相対論的な場合、type Iの状況ではそもそもvortex解が存在しません。

そのほかのこと

2つほどコメントです。

1. 一般にBPS解の性質は有用です。例えばDブレーン（超弦理論の低エネルギー有効理論である超重力理論におけるソリトン解）のRamond-Ramond chargeという量を計算する際には、BPS状態のDブレーンの性質が利用されますOhta2002。またSeiberg-Witten理論において、 ${\cal N}=2$超対称Yang-Mills理論における低エネルギー有効理論はBPS状態のゼロ質量粒子（モノポールとダイオン）で書けるという予想がされる際にも、BPS状態の性質が使われます。
2. vortexの端点にはmagnetic monopoleが付随することができます。このmonopole-vortex系のエネルギーは、vortexの長さに比例します。このため有限のエネルギーではmonopoleを無限に引き離すことができません。これは有限のエネルギーで電荷・物体を無限遠まで引き離せる電磁気力・重力とは著しく異なります。このような現象を「閉じ込め」と呼びます。クォークはハドロン内に閉じ込められていますが、それを強い相互作用の真空の超伝導性で説明する理論が存在します。これを「双対超伝導描像」と呼びますKondo2005。

まとめ

第2種超伝導体内に侵入した磁束のモデルであるNielsen-Olesen vortexに関して述べました。Abelian Higgs模型はGinzburg-Landau理論から導かれる有効作用です。解に関して軸対称のansatzをおき、遠方で真空の配位に近づく紐状・渦状のvortex解を探します。このvortexは磁束を持ち、それは量子化されることがわかります。

BPS limit:$\lambda=q^2$では運動方程式が簡単になります。これを数値的に解き、実際にvortex解を求めました。$\rho$が小さいところでは$B$は有限、$\phi$はゼロ、$\rho$が大きいところではその逆になります。Higgs機構によりAH系が持つU(1)対称性は自発的に破れ、ゲージ場は質量$m_V$を獲得しますが、$B$が減少する位置はこの質量の逆$\rho\simeq m_V^{-1}=1/(\sqrt{2}q\phi_0)$付近です。一方Higgs場$\phi$はその質量$m_H$の逆$\rho\simeq m_H^{-1}=1/(\sqrt{2\lambda}\phi_0)$のあたりで増大します。BPS limitでは$m_V=m_H$です。

vortex間の相互作用は$m_V, m_H$の大小で変化します。$m_V< m_H$なら斥力であり、これがtype IIに相当します。一方$m_V>m_H$の場合引力であり、このとき複数のvortexは安定には存在できず、type Iに相当します。ただし実際の超伝導体のように非相対論的な場合、type Iに相当するケースではそもそもvortex解自体存在しません。

おしまい。${}_\blacksquare$

• 注1: ピン留めという言葉、またそのイメージから推測すると、磁石の上に浮上している超伝導体は回転もできないように思えます。しかしこれは間違っていて、超伝導体は磁石上で非常になめらかに回転します。また磁石のレールの上を超伝導体がなめらかに走ることも可能です。
• 注2: マイスナー効果のもうひとつの重要な事実に「電気抵抗がゼロになる」があります。これには、超伝導状態における準粒子の励起にCooper対の凝縮により定まるエネルギーギャップが必要であることが関わります。このエネルギーギャップにより、電子の流れが変化するような散乱のエネルギーが高くなり、散乱が起きなくなることで抵抗がゼロになります。