要素が全部aの正方行列の固有多項式を対合で求める

正方行列$A_n=(a)_{i,j=1}^n$を，要素が全部$a$の$n\times n$行列とする ($a$は定数)．本稿では$A_n$の固有多項式を，組合せ論を使う方法で計算する．

証明に入る前にグラフの閉路と行列式の関係について復習する．
有限有向グラフ$G$の部分グラフで，各節点の入次数と出次数が$1$であるものの集合を$\mathcal{C}(G)$とかく．
グラフ$H\in\mathcal{C}(G)$は，より平易に言えば，$G$に含まれる互いに疎な閉路をいくつか集めてきてできるグラフである．
グラフ$H\in\mathcal{C}(G)$の連結成分の数を$c(H)$とかく．また，$H$に含まれない$G$の節点の数を${\rm ip}(H)$とかく．

また，グラフ$G$には枝重み$e\colon E(G)\to\mathbb{C}$が付けられているとし，$G$の部分グラフ$H$に対して$w(H)\triangleq\prod_{e\in E(H)}w(e)$で$H$に含まれる枝重みの積を表すとする．
以下のことが知られている．

この事実の証明は例えば [1]を参照してほしい．
ここでは，定理2の証明は書かず具体例を紹介するにとどめておく．

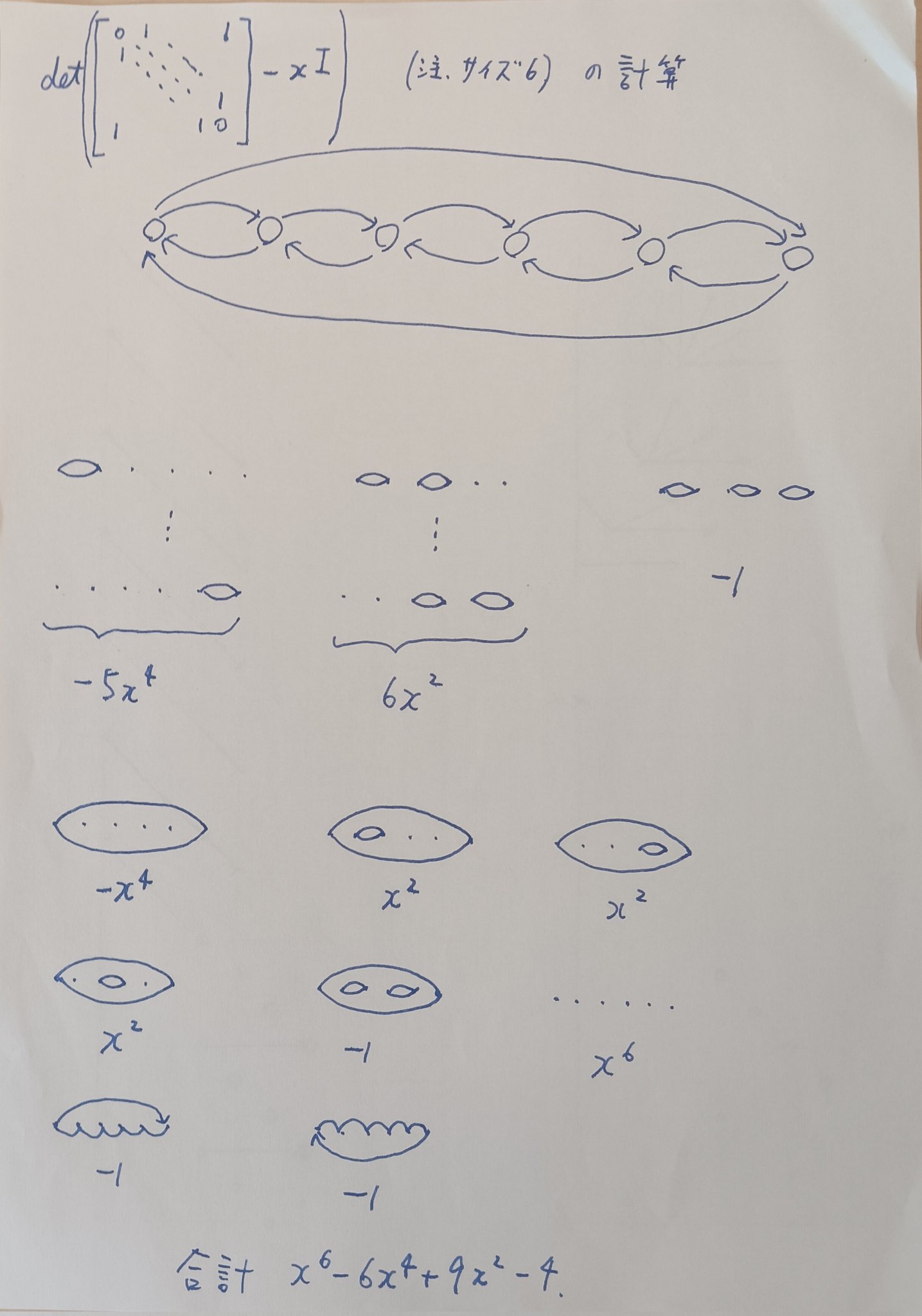
定理1の証明．

定理2を使うと，計算したい行列式$\det(A_n-xI_n)$は，
\begin{align} \det(A_n-xI_n)=\sum_{H\in \mathcal{C}(K_n)} (-1)^{n-c(H)}x^{{\rm ip}(H)}a^{|E(H)|} \end{align}
と書ける．ただし，$K_n$は$n$節点の完全有向グラフに，全ての節点へ自己ループを加えてできる有向グラフを表す（下図左を見よ．）

集合$\mathcal{C}(K_n)$の部分集合$\mathcal{S}_n$を，枝のない部分グラフと，自己ループ$1$個だけからなる部分グラフを集めた集合と定義する．例えば，$n=7$のとき$\mathcal{S}_7$は下図右のようになる．

左：$K_7$．枝は双方向に張られているとする．右：$\mathcal{S}_7$の元．

定理1の右辺は，この集合$\mathcal{S}_n$にわたる和として
\begin{align} \sum_{H\in \mathcal{S}_n} (-1)^{n-c(H)}x^{{\rm ip}(H)}a^{|E(H)|} = (-1)^n(x^n-nax^{n-1}) \end{align}
とかける．

よって，我々が示すべきことは，集合$\mathcal{C}(K_n)\setminus \mathcal{S}_n$にわたる重みの和が$0$になること，すなわち
\begin{align} \sum_{H\in \mathcal{C}(K_n)\setminus\mathcal{S}_n} (-1)^{n-c(H)}x^{{\rm ip}(H)}a^{|E(H)|} =0 \end{align}
である．

これを示すには，枝の数を変えずに，閉路の数を$1$だけ変化させるような対合
$\varphi:\mathcal{C}(K_n)\setminus\mathcal{S}_n\to\mathcal{C}(K_n)\setminus\mathcal{S}_n$
を作ればよい．

グラフの節点を$\{1,2,\ldots,n\}$とラベル付けする．
$H\in\mathcal{C}(K_n)\setminus\mathcal{S}_n$とする．グラフ$H$に含まれる節点の中で，ラベルが最小の節点 ($i$とする)と二番目に小さい節点 ($j$とする)に注目する．

• $i$と$j$が同じサイクルに含まれる場合，サイクルを二つに分離する．
  つまり，$(i,x_1,\ldots,x_r,j,y_1,\ldots,y_t)$というサイクルを，$(i,x_1,\ldots,x_r),(j,y_1,\ldots,y_t)$という二つのサイクルに分ける．
• $i$と$j$が違うサイクルに含まれる場合，サイクルを一つに融合する．
  つまり，$(i,x_1,\ldots,x_r),(j,y_1,\ldots,y_t)$という二つのサイクルを$(i,x_1,\ldots,x_r,j,y_1,\ldots,y_t)$という一つのサイクルにする．

それ以外の部分は変化させない．
この操作を$\varphi$とすれば，これは所望の対合である．

対合$\varphi$のようす

（証明終わり．）