文献あり

Tree Metric and Ultra Metric

165

はじめに

頂点集合と正の重みのついた辺集合からなるグラフを考え、2頂点間の最短距離を考えると、それは有限距離空間になっています。逆に、有限距離空間が与えられたとき、頂点集合を距離空間の元、頂点間には距離の重みを持つ辺を張ることでグラフを考えることができます。
この記事では、有限距離空間がグラフの中でも特に閉路を含まないグラフである木で表されるための必要十分条件について説明します。

距離空間 (metric space)

$X$ を有限集合、 $d : X \times X \to R_{\geq 0}$ としたとき、 $(X, d)$ が次の3つの条件を満たす時、距離空間(metric space)であるという。

$\forall x \in X$ $d (x, y) = 0 \Leftrightarrow x = y$
$\forall x, y \in X$ $d (x, y) = d (y, x)$
$\forall x, y, z \in X$ $d (x, z) \leq d (x, y) + d (y, z)$

辺に重みのついた木 $T = (V, E)$ が与えられた時、 $x, y \in V$ について $d_{T} (x, y)$ は $T$ に存在する $x, y$ パスに含まれる辺の重みの総和を表すことにします。

木距離 (Tree Metric)

有限距離空間 $(X, d)$ が木距離(Tree Metric)であるとは、辺重み付き木 $T = (V, E) (X \subseteq V)$ が存在して、
$\forall x, y \in X$ $d_{T} (x, y) = d (x, y)$ が成り立つことである。

木距離を考える際は、必ずしも $X = V$ ではありません。例えば距離空間として
$X = {1, 2 . . . n}$ , $\forall i \neq j \in X, d (i, j) = 1$ を考えます。
このとき頂点を1つ付け足し、 $n + 1$ 頂点のstar graphをつくり、各辺に重み $1 / 2$ を割り当てることで、木距離として表せます。

$V ∖ X$ の頂点をSteiner Nodeといいます。次数2のSteiner Nodeは自明に消すことができるため、考えません。

4PC (four point condition)

有限距離空間 $(X, d)$ が4PCを満たすとは、すべての異なる4点 $x, y, z, w \in X$ について、 $d (x, y) + d (z, w) \leq max (d (x, z) + d (y, w), d (x, w) + d (y, z))$
が成り立つことである。

4PCの条件を言い換えることもできます。
$d_{x y, z w} = d (x, y) + d (z, w)$ と書きます。4PCの条件を書いてみると、
$d_{x y, z w} \leq max (d_{x z, y w}, d_{x w, y z})$
$d_{x z, y w} \leq max (d_{x y, z w}, d_{x w, y z})$
$d_{x w, y z} \leq max (d_{x y, z w}, d_{x z, y w})$
が成り立ちますが、これは $d_{x y, z w}, d_{x z, y w}, d_{x w, y z}$ の最大値がユニークではないこと(e.g. 7, 7, 3 や 7, 7, 7など)と同値です。こちらの条件の方がわかりやすかったりするので、こちらを使うときもあります。

実は4PCを満たすこととTree Metricであることは同値です。
まず、補題を示します。

$x, y, w, z \in X$ が $d_{x y, z w} \leq d_{x z, y w} = d_{x w, y z}$ を満たす。
$\Leftrightarrow$ 　 $x, y, z, w$ は図1のような木 $T$ で距離を表せる (必ずしも $u \neq x$ などとは限らない)。
木!FORMULA[38][37236][0] 木 $T$
また、特に等号が成り立つ時、 $u = u^{'}$ である。

$\Leftarrow$ を示す。
$d (x, y) + d (z, w) = d_{T} (x, u) + d_{T} (u, y) + d_{T} (z, u^{'}) + d_{T} (u^{'}, w)$
$d (x, z) + d (y, w) = d (x, w) + d (y, z) = d_{T} (x, u) + d_{T} (u, y) + d_{T} (z, u^{'}) + d_{T} (u^{'}, w) + 2 \cdot d_{T} (u, u^{'})$
より、 $d (x, z) + d (y, w) = d (x, w) + d (y, z) \geq d (x, y) + d (z, w)$ だから4PCを満たす。また $u = u^{'}$ のとき、 $d_{T} (u, u^{'}) = 0$ より等号が成り立つ。
$\Rightarrow$ を示す。
図1のような木 $T$ を考え、
$d_{T} (x, u) = \frac{d (x, y) + d (x, z) - d (y, z)}{2}$
$d_{T} (y, u) = \frac{d (y, x) + d (y, z) - d (x, z)}{2}$
$d_{T} (z, u^{'}) = \frac{d (z, w) + d (z, x) - d (x, w)}{2}$
$d_{T} (w, u^{'}) = \frac{d (w, z) + d (w, x) - d (x, z)}{2}$
$d_{T} (u, u^{'}) = \frac{d (x, z) + d (y, w) - d (x, y) - d (z, w)}{2}$
とすれば、 $T$ 上の距離と $d$ は等しくなっている。( $d_{T} (x, u), d_{T} (y, u), d_{T} (z, u^{'}), d_{T} (w, u^{'}) \geq 0$ は三角不等式より、 $d_{T} (u, u^{'}) \geq 0$ は4PCの条件より成り立つ。)
例えば、
$\begin{array}{rcl} d_{T} (x, z) & = & d_{T} (x, u) + d_{T} (u, u^{'}) + d_{T} (u^{'}, z) \\ = & d (x, z) + d (x, z) + d (y, w) - d (y, z) - d (x, w) \\ = & d (x, z) \end{array}$
他も同様。
また等号が成り立つ時 $d_{T} (u, u^{'}) = 0$ より $u = u^{'}$

有限距離空間 $(X, d)$ がTree Metricである。 $\Leftrightarrow$ 4PCを満たす。

$\Rightarrow$ を示す。
木距離で表されるのだから、木 $T = (V, E)$ が存在して、 $T$ 上の距離は $d$ と一致している。
任意の4点 $x, y, z, w \in X \subseteq V$ を取る。距離は木 $T$ で表されているから、4点の全点対間パスからなる部分グラフを取ると一般性を失わず、補題1図1のようになっている。(必ずしも $u \neq u^{'}, u \neq x$ など、とは限らない。)つまり、4PCを満たす。

$\Leftarrow$ を示す。
距離空間の集合の元の数に関する帰納法で示す。
$| X | \leq 3$ のときは自明である。
$| X | \geq 4$ のとき、
帰納法の仮定より $| X | - 1$ 個の元を含む木 $T = (V, E)$ が存在している。
新たに頂点 $v \in X$ を距離 $d$ にあうように $T$ に付け足す。
2つの場合に分ける。
(1) すべての $x, y, z \in V \cap X$ について、 $d_{x y, z v} = d_{x z, y v} = d_{x v, y z}$ のとき。
ある $x, y, z \in V \cap X$ をとり、 $T$ 上の $x y, y z, z x$ パスが誘導するグラフを考える。
$T$ は木であるから、一般性を失うことなく、図2のように書ける(必ずしも $x \neq u$ など、とは限らない)。

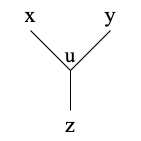
頂点 $v$ を $u$ から $w = \frac{d (x, v) + d (y, v) - d (x, y)}{2}$ の重みの辺でつなぎ新たに木 $T^{'}$ を作る。 $T^{'}$ が求めていた木になっていることを示す。
補題1と $w$ の選び方より、 $x, y, z$ と $v$ の間では $d$ と $d_{T^{'}}$ が等しいことがわかる。
よって $x, y, z$ 以外の $z^{'} \in V \cap X$ について $d_{T^{'}} (z^{'}, v) = d (z^{'}, v)$ を示す。
$T$ 上の $x y, y z^{'}, z^{'} x$ パスが誘導するグラフを考える。一般性を失わず、図3のようになっている。

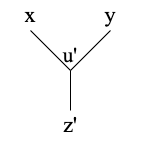
$w_{z}$ 同様に $w_{z^{'}}$ を定める。この時次の3式が成り立つ。

$d_{T} (x, u) + w_{z} = d_{T} (x, u^{'}) + w_{z} (= d (x, v))$
$d_{T} (y, u) + w_{z} = d_{T} (y, u^{'}) + w_{z} (= d (y, v))$
この式を満たすには $d_{T} (x, u) = d_{T} (x, u^{'}), d_{T} (y, u) = d_{T} (y, u^{'})$ となるしかない。よって $u = u^{'}$ つまり $z^{'}$ も $z$ と同様の議論で $d (z, v) = d_{T^{'}} (z, v)$ である。

(2) (1)でないとき
ある $x, y, z \in X \cap V$ が存在して、 $d_{x y, z v} < d_{x z, y v} = d_{x v, y z}$ となっている。 $T$ 上の $x y, y z, z x$ パスが誘導するグラフを考えると図2のようなグラフになっているとしてよい。
$u$ を取り除くと $T$ はいくつかの連結成分に分かれる。 $z$ を含む連結成分を $C_{0}$ として、
その他の連結成分を $C_{1}, . . ., C_{k}$ とする。
このとき、 $\forall 1 \leq i \leq k, \forall w \in C_{i}$ について、 $d (w, v) = d_{T} (w, u) + \frac{d (x, v) + d (y, v) - d (x, y)}{2}$ ・・・(i)であることを示す。
これを示せば、距離の条件に $d (u, v) = \frac{d (x, v) + d (y, v) - d (x, y)}{2}$ を加え $u + C_{0}$ について同様の手続き(3点選んで $v$ を挿入する適切な位置を探す)をすれば良い。 $u + C_{0}$ は $T$ よりも真に頂点数が少なくなっているので、(1)のケースが起きるか、頂点数が2となる時に操作が終了する。頂点数が2となった時は2点の間の辺を距離に応じて適当に分割して新たな頂点を作り、そこから辺を伸ばして $v$ を付け足せば良い。

(i)を示す。

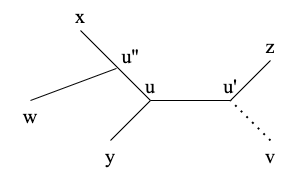
$w$ が $y$ と同じ連結成分に属する時以外は図4のような位置関係にあるとして良い。( $u \neq u^{″}$ とは限らないことに注意)
また真に不等号が成り立っているから $u \neq u^{'}$ である。
$x, y, z, v$ と $x, y, z, w$ の4PCより、
$d (x, y) + d (z, v) < d (x, z) + d (y, v) = d (x, v) + d (y, z) (ii)$
$d (x, w) + d (y, z) \leq d (x, y) + d (w, z) = d (x, z) + d (w, y) (iii)$
が成り立つ。
よって
$\begin{array}{rcl} d (x, w) + d (z, v) & < & (d (x, y) + d (w, z) - d (y, z)) + (d (x, v) + d (y, z) - d (x, y)) (ii), (iii) より \\ = & d (x, v) + d (w, z) \end{array}$
よって $x, w, z, v$ の4PCを考えると、
$d (x, w) + d (z, v) < d (x, v) + d (w, z) = d (x, z) + d (w, v)$ (iv)
が成り立つ。
$\begin{array}{rcl} d_{T} (w, u) + \frac{d (x, v) + d (y, v) - d (x, y)}{2} & = & \frac{d_{T} (w, y) + d_{T} (w, z) - d_{T} (y, z)}{2} + \frac{d (x, v) + d (y, v) - d (x, y)}{2} \\ = & \frac{d (w, y) + d (w, z) - d (y, z)}{2} + \frac{d (x, v) + d (y, v) - d (x, y)}{2} \\ = & \frac{(d (x, y) + d (w, z) - d (x, z)) + d (w, z) - d (y, z)}{2} \\ + \frac{d (x, v) + (d (x, v) + d (y, z) - d (x, z)) - d (x, y)}{2} (ii), (iii) より \\ = & d (x, v) + d (w, z) - d (x, z) \\ = & d (w, v) (iv) より \end{array}$
$w$ が $y$ と同じ連結成分に属する時は $x, y$ を入れ替えて、同様の議論をすれば良い。

上の命題の証明から次のこともわかる。

Tree Metricを表現する木の一意性

有限距離空間 $(X, d)$ がTree Metricであるとき、距離を表現する木は一意である。

4PCと似た条件で3PCが知られています。

3PC (three point condition)

有限距離空間 $(X, d)$ が3PCを満たすとは、すべての異なる3点 $x, y, z \in X$ について、
$d (x, y) \leq max (d (x, z), d (y, z))$ が成り立つことである。

4PC同様、この条件は $d (x, y), d (x, z), d (y, z)$ の最大値がユニークではないことと同値です。また3PCの条件を繰り返し適用することで以下も分かります。

UltraMetricの性質1

$t_{0}, t_{1}, . . ., t_{k} \in X$ とする。
このとき、 $d (t_{0}, t_{k}) \leq max_{0 \leq i < k} d (t_{i}, t_{i + 1})$ が成り立つ。

3PCを満たす距離はUltra Metricと呼ばれます。

Ultra Metric

有限距離空間 $(X, d)$ がUltra Metricである。 $\Leftrightarrow$ $(X, d)$ が3PCを満たす。

3PC

\to

4PC

有限距離空間 $(X, d)$ が3PCを満たすなら、4PCを満たす。

ひたすら、場合分けして証明します。3PCの条件によって $x, y, z, w$ の位置関係を見て、成り立つであろう4PCの式を推定して、証明していく気持ちです。

異なる4点 $x, y, z, w \in X$ を任意に取る。
3PCを満たすから、一般性を失うことなく、 $d (x, y) \leq d (x, z) = d (y, z)$ ・・ $(i)$ としてよい。
$x, y, w$ の3PCの条件について、2通りの場合を考える。
(1) $d (x, y) \leq d (x, w) = d (y, w)$ ・・ $(1)$ のとき、
$(i), (1)$ より、 $d (y, z) + d (x, w) = d (y, w) + d (x, z)$ である。
$x, w, z$ の3PCの条件より、 $d (w, z) \leq max (d (x, w), d (x, z))$ である。
$d (w, z) \leq d (x, w)$ のときは、 $d (x, y) + d (w, z) \leq d (y, z) + d (x, w)$ $(i)$ より
$d (w, z) \leq d (x, z)$ のときは、 $d (x, y) + d (w, z) \leq d (y, w) + d (x, z)$ $(1)$ より
が成り立つ。
いずれの場合も $d (x, y) + d (w, z) \leq d (y, z) + d (x, w) = d (y, w) + d (x, z)$ となり、4PCが成り立つ。
(2) $d (x, w) \leq d (x, y) = d (y, w)$ ・・ $(2)$ のとき、
$(i), (2)$ より、 $d (x, w) \leq d (x, y) \leq d (x, z)$ ・・ $(ii)$ が成り立つ。
$(ii)$ の不等号が全て等号であるとき、 $d (x, w) = d (x, z)$ となる。 $x, w, z$ の3PCの条件より、 $d (w, z) \leq d (x, w) = d (x, z)$ である。このとき、 $(i), (2)$ の等号もすべて成立し、 $d (x, y) + d (w, z) \leq d (y, z) + d (x, w) = d (y, w) + d (x, z)$ となり、4PCが成り立つ。
$(ii)$ の不等号が等号でないことがあるとき、 $d (x, w) < d (x, z)$ となる。 $x, w, z$ の3PCの条件より、 $d (x, w) < d (x, z) = d (w, z)$ ・・ $(iii)$ である。このとき、 $(2)$ と合わせると、
$d (x, y) + d (w, z) = d (y, w) + d (x, z)$ である。 $(i), (2)$ より、 $d (x, w) + d (y, z) \leq d (y, w) + d (x, z)$ だから4PCが成立する。

命題3よりUltra MeticはTree Metricです！つまり、Ultra Metricであるような距離はなんらかの木で距離を表すことができます。さらにUltra Metricは特別な性質を持つ木で表せるTree Metricになっていることが示せます。そのことを示すために、以下の補題を示します。

辺重み付きの木を $T = (V, E)$ としたとき、 $x, y \in V$ について、 $δ_{T} (x, y)$ を $T$ 上の $x, y$ パスに含まれる辺で最大の辺重みとします。 $δ_{T}$ は距離の公理を満たします。

Ultra Metric を生成する木

有限距離空間 $(X, d)$ がUltra Meticである。 $\Leftrightarrow$ ある木 $M = (X, E)$ が存在して、 $\forall x, y \in X$ $d (x, y) = δ_{M} (x, y)$ が成り立つ。

$\Rightarrow$ を示す。
$X$ の各頂点対 $x, y$ を $d (x, y)$ の辺重みで繋いだグラフ $G$ 、 $M$ を $G$ の最小全域木とする。
Ultra Metricの性質1より、 $M$ 上の $x, y$ パスを $x = t_{0}, t_{1}, . . ., t_{k} = y$ とすると、
$d (x, y) \leq max_{0 \leq i < k} d (t_{i}, t_{i + 1}) = max_{0 \leq i < k} δ_{M} (t_{i}, t_{i + 1}) = δ_{M} (x, y)$
また、 $M$ は $G$ の最小全域木であることから、 $δ_{M} (x, y) \leq d (x, y)$ である。
つまり $d (x, y) = δ_{M} (x, y)$
$\Leftarrow$ を示す。
$x, y, z \in X$ をとり、 $M$ 上の $x y, y z, z x$ パスが誘導するグラフを考える。そのグラフ上で最大辺重みである辺を考えると、それは $x y, y z, z s$ パスの少なくとも2つに属している。よって $δ_{M} (x, y), δ_{M} (y, z), δ_{M} (z, x)$ の最大値はユニークではない。つまり3PCを満たす。

補題4で存在が示される木を「Ultra Metricを生成する木(generating tree for ultrametric)」と言います。

有限距離空間 $(X, d)$ がUltra Meticであるなら、距離 $d$ を表す木 $T = (V, E)$ と根 $r \in V$ が存在して、すべての $x \in X$ について、 $d_{T} (r, x)$ が等しい。

$| X |$ に関する帰納法で、命題5の条件に「 $d_{T} (r, x)$ は $\frac{1}{2} max_{x, y \in X} d (x, y)$ 以下である。」も加えた命題を示す。

$| X | = 1$ の時は自明である。 $| X | > 1$ の場合を示す。
Ultra Metric $(X, d)$ を生成する木を $M$ とする。 $M$ の辺で重みが最大であるような辺を $e = x y$ とし、その重みを $w_{e}$ とする。 $M$ から $e$ を取り除くと、2つの木ができる。これを $M_{1}, M_{2}$ とする。帰納法の仮定から $δ_{M_{i}}$ について、 $T_{i} = (V_{i}, E_{i})$ と $r_{i} \in V_{i}$ が存在して、帰納法の条件を満たす。 $e$ の選び方より、すべての $x \in V_{i}$ について、 $d_{T_{i}} (r_{i}, x) \leq \frac{1}{2} w_{e}$ を満たす。よって、 $T = (V_{1} \cup V_{2} \cup {r}, E_{1} \cup E_{2} \cup {r r_{1}, r r_{2}})$ として、辺 $r r_{i}$ の重みをそれぞれ、 $\frac{1}{2} w_{e} - d_{T_{i}} (r_{i}, x)$ とすれば、条件を満たす。