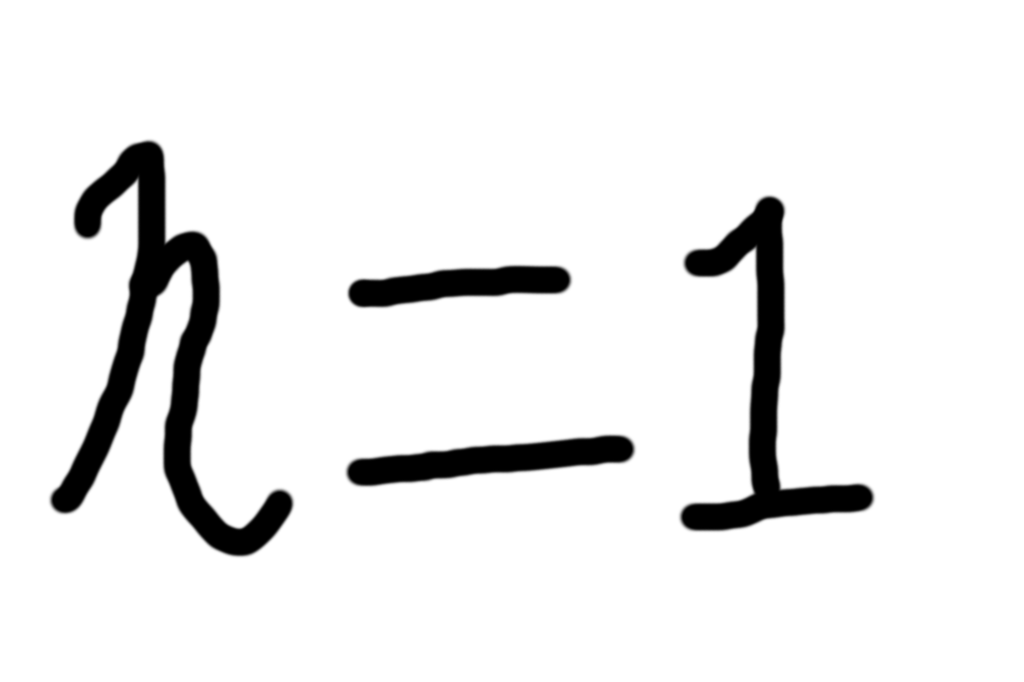テトレーションの逆関数
はじめに
こんにちは、円周率の日が過ぎてしまったのn=1です。今回は 前回 の続きになる、高さが決まっているときの テトレーション の逆関数、つまり$^nx$($n$は定数)の逆関数についてやっていきます。
本題
おさらいとして
前回
は、式を変形して$f(x)=xe^{xe^x}$の逆関数を求めることで最終的に$^3x$の逆関数(以下$\sqrt[3]{x}_s$)を求めました。
今回も同じように変形するところから始めます。ただし、$\sqrt[n]{x}_s$の形で出したいので、今回は$^ny=x$の形から変形させます。
$^ny=x$
$^{n-1}y\ln(y)=(\ln(y))e^{^{n-2}y\ln(y)}=\underbrace{(\ln(y))e^{(\ln(y))e^{ \cdot^{\cdot^{\cdot^{(\ln(y))e^{(\ln(y))}}}}}}}_{n個}=\ln(x)$
そのため今回も$f_n(x)=\underbrace{xe^{xe^{\cdot^{\cdot^{\cdot^{xe^x}}}}}}_{xがn個}(f_2(x)=xe^x,f_{n+1}(x)=xe^{f_{n}(x)})$という風に定義して$f^{-1}_n(x)$を求めます。
$f^{-1}_n(x)$は
$f_n(0)=0e^{0e^{\cdot^{\cdot^{\cdot}}}},f'_n(0)=e^{0e^{\cdot^{\cdot^{\cdot}}}}+0 \frac{d}{dx}e^{0e^{\cdot^{\cdot^{\cdot}}}}=1 \neq 0$
なので
ラグランジュ反転定理
で
$$f^{-1}_n(x)=\sum_{k=1}^{∞} \frac{x^k}{k!} \lim_{t \to 0} \frac{d^{k-1} }{dt^{k-1}}( \frac{t}{f_n(t)} )^k=\sum_{k=1}^{∞} \frac{x^k}{k!}\lim_{t \to 0} \frac{d^{k-1} }{dt^{k-1}}\underbrace{e^{-kte^{te^{{\cdot^{\cdot^{\cdot^t}}}}}}}_{n-1}=\sum_{k=1}^{∞} \frac{x^k}{k!}\lim_{t \to 0} \frac{d^{k-1} }{dt^{k-1}}e^{-kf_{n-1}(t)}$$
これはまた$e^{\alpha f_{n-1}(x)}$のm回微分を
ファー・ディ・ブルーノの公式
などを使い求めて
$$
\frac{d^m}{dx^m}e^{\alpha f_{n-1}(x)}=e^{\alpha f_{n-1}(x)}B_m{(\alpha f'_{n-1}(x),\alpha f''_{n-1}(x),\cdots,\alpha f^{(m)}_{n-1}(x))}
$$
これまたm回微分を求めて
$$
\frac{d^m}{dx^m}f_{n}(x)=\frac{d^m}{dx^m}xe^{f_{n-1}(x)}=m\frac{d^{m-1}}{dx^{m-1}}e^{f_{n-1}(x)}+x\frac{d^m}{dx^m}e^{f_{n-1}(x)}
$$
まとめ
これを組み合わせれば求まるので結果をまとめると
$^ny=x \Longleftrightarrow (y=)\sqrt[n]{x}_s=e^{f^{-1}_n(\ln(x))}$ $(f_n(x)=\underbrace{xe^{xe^{\cdot^{\cdot^{\cdot^{xe^x}}}}}}_{xがn個})$
$$f^{-1}_n(x)=\sum_{k=1}^{∞} \frac{x^k}{k!}\lim_{t \to 0}e^{-kf_{n-1}(t)}B_{k-1}{(-kf'_{n-1}(t),-kf''_{n-1}(t),\cdots,-kf^{(k-1)}_{n-1}(t))}$$
$$\frac{d^m}{dx^m}f_{n}(x)=me^{f_{n-1}(x)}B_{m-1}{(f'_{n-1}(x),f''_{n-1}(x),\cdots,f^{(m-1)}_{n-1}(x))}+xe^{f_{n-1}(x)}B_m{(f'_{n-1}(x),f''_{n-1}(x),\cdots,f^{(m)}_{n-1}(x))}$$
が答えと分かります。前回同様$B_n(x_1,\cdots,x_n)$は
n次完全ベル多項式
です。
最後に
余談ですが上の式をまとめて上手く一般化してテトレーションが一般化できないかなーと思いました。
以上で今回の$\sqrt[n]{x}_s$の一般化(nは定数)は終わりです。間違っている部分がありましたらご指摘のほどお願いします。投稿を見てくださりありがとうございました。