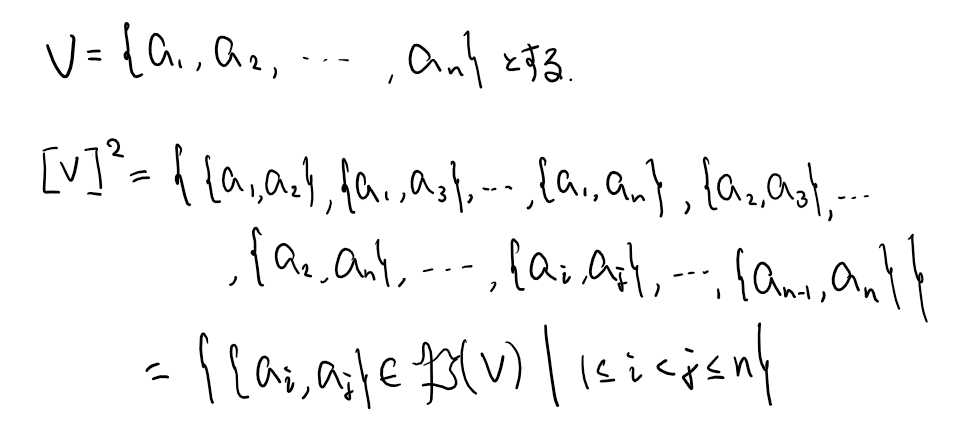〔位相空間論〕 距離空間 part1.~グラフ理論を添えて~
今回から数回にわけて位相空間論の基礎について解説していきたいと思います.
めんどいので辞めます. (2024/6/5)
今回は「〔位相空間論〕 距離空間 part1.~グラフ理論を添えて~」です. 距離空間の定義と例及びグラフ理論における距離を解説していきます.
用語
これからの位相空間論の記事では以下の記号を断りなく使うことがある.
$\mathbb{R}$:実数全体の集合. $\mathbb{Q}$:有理数全体の集合. $\mathbb{Z}$:整数全体の集合. $\mathbb{N}$:自然数全体の集合
以降適宜追加していく.
距離空間の定義と例
$X$を空でない集合とする. 関数$d:X\times X \rightarrow \mathbb{R}$が次の3つ条件を満たすとき, 関数$d$を集合$X$上の距離関数と呼ぶ.
任意の$x,y,z\in X$に対して
(1) $d(x,y) \ge 0$である. そして, $d(x,y) = 0 \Leftrightarrow x = y$.
(2) $d(x,y) = d(y,x)$.
(3) $d(x,z) \le d(x,y) + d(y,z)$.
上の3つの条件を距離の公理と呼ぶ.
条件(3)を三角不等式と呼ぶ.
$X$を空でない集合とし, $d$を集合$X$上の距離関数とする.
このとき, 対$(X,d)$を距離空間という.
$X$の元を点と呼ぶ.
単に$X$を距離空間と呼ぶこともある.
距離空間の例をいくつか挙げる.
ユークリッド空間
$\mathbb{R}$の$n$個の直積を$\mathbb{R}^n$と表す.
$\mathbb{R}^n$の元$x=(x_1,x_2,\dots ,x_n)$, $y=(y_1,y_2,\dots ,y_n)$に対して, 関数$d^{(n)}:\mathbb{R}^n\times \mathbb{R}^n \rightarrow \mathbb{R}$を以下のように定める.
$$
d^{(n)}(x,y) = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots +(x_n-y_n)^2}
$$
先の記号のもとで,
$d^{(n)}$をユークリッド距離といい, 対$(\mathbb{R}^n, d^{(n)})$を$n$次元ユークリッド空間という.
$d^{(n)}$は距離関数となり, $(\mathbb{R}^{n},d^{(n)})$は距離空間となる.
距離の公理を満たすことを示せばよい.
$x,y,z\in \mathbb{R}^{n}$で,
$x=(x_1,x_2,\dots ,x_n)$, $y=(y_1,y_2,\dots ,y_n)$, $z=(z_1,z_2,\dots ,z_n)$と表そう.
(1)
$d^{(n)}(x,y) = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots +(x_n-y_n)^2}$より$d^{(n)}(x,y)\ge 0$であることは明らか.
\begin{eqnarray}
d^{(n)}(x,y)=0 &\Leftrightarrow & \sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots +(x_n-y_n)^2}=0\\
&\Leftrightarrow &(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)^2=0\\
&\Leftrightarrow& x_1-y_1=0,x_2-y_2=0,\dots,x_n-y_n=0\\
&\Leftrightarrow& x_1=y_1,x_2=y_2,\dots,x_n=y_n\\
&\Leftrightarrow& x=y.
\end{eqnarray}
(2)
\begin{eqnarray}
d^{(n)}(x,y)&=&\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots +(x_n-y_n)^2}\\
&=&\sqrt{(y_1-x_1)^2+(y_2-x_2)^2+\cdots +(y_n-x_n)^2}\\
&=&d^{(n)}(y,x).
\end{eqnarray}
(3)
$a_i=x_i-y_i, b_i=y_i-z_i(1\le i \le n)$とおく.
$a_i+b_i=x_i-z_i$であるから,
\begin{eqnarray}
(d^{(n)}(x,z))^2&=&\sum_{i=1}^{n}(x_i-y_i)^2\\
&=&\sum_{i=1}^{n}(a_i+b_i)^2\\
&=&\sum_{i=1}^{n}a_i^2+\sum_{i=1}^nb_i^2+2\sum_{i=1}^n(a_ib_i)\\
&\le&\sum_{i=1}^{n}a_i^2+\sum_{i=1}^nb_i^2+2\sqrt{(\sum_{i=1}^na_i^2)(\sum_{i=1}^nb_i^2)}\\
&=& \left( \sqrt{\sum_{i=1}^na_i^2}+\sqrt{\sum_{i=1}^nb_i^2}\right)^2\\
&=&(d^{(n)}(x,y)+d^{(n)}(y,z))^2.
\end{eqnarray}
従って,
$$
d^{(n)}(x,z)\le d^{(n)}(x,y)+d^{(n)}(y,z).
$$
(1), (2), (3)より$d^{(n)}$は距離関数であり, $\mathbb{R}^n$は空集合ではないので, $(\mathbb{R}^n,d^{(n)})$は距離空間となる.
3行目から4行目の変形では次のシュワルツの不等式を用いた.
シュワルツの不等式
任意の実数$a_1,\dots,a_n$, $b_1,\dots,b_n$に対して
$$
(\sum_{i=1}^na_ib_i)^2\le (\sum_{i=1}^na_i^2) \cdot (\sum_{i=1}^nb_i^2)
$$
が成り立つ.
証明は簡単のため省略する. (右辺-左辺を計算すればそれが0以上であることがわかる.)
(3)において$a_i=x_i-y_i, b_i=y_i-z_i(1\le i \le n)$としたのはいささか技巧的に見えるかもしれないが, $d^{(n)}(x,z)$, $d^{(n)}(x,y)$, $d^{(n)}(y,z)$を考えれば自然な方法であることがわかるだろう.
少し詳しく書きすぎたかもしれない. 今後はここまで詳しく書かないが自分で行間を埋めながら読んでほしい.
離散距離空間
$X$を空でない集合とし, 関数$d:X\times X\rightarrow \mathbb{R}$を次で定める.
$x,y\in X$に対して
$$
d(x,y)= \begin{eqnarray}
\left\{
\begin{array}{l}
1 \quad (x\ne y)\\
0 \quad (x=y)
\end{array}
\right.
\end{eqnarray}
$$
$d$を$X$上の離散距離といい対$(X,d)$を離散距離空間という.
空でない集合$X$上の離散距離$d$が距離関数であることを示せ.
クリックして略解をチェック
距離の公理(1)~(3)を満たすことを示せばよい.
$x,y,z\in X$とする.
(1), (2)は明らかだろう.
(3)は$x=z$と$x\ne z$で場合分けすると良い.
これより, 離散距離空間は距離空間となる.
コラム:tea break
グラフと距離
tea break がtea break であるために厳密さを欠くところがありますがご了承ください. (詳しく知りたい方は, グラフ理論の本を手に取ってみると良いです. )
グラフとは, 点と点同士をつなぐ辺の集まりである.
(単純無向)グラフとは空でない有限集合$V$と$E$との組$(V,E)$のことである. $V$の冪集合$\mathfrak{P}(V)$の部分集合のうち, 2つの元からなる集合全体のなす集合を$[V]^2$で表し, $[V]^2$の部分集合を$E$とする.
$V,E$をそれぞれ頂点集合, 辺集合と呼ぶ.
頂点集合の元を頂点, 辺集合の元を辺と呼ぶ.
$E=[V]^2$のとき, グラフを完全グラフと呼ぶ.
$V,E$からなるグラフ$G$を$G=(V,E)$などと書く.
$[V]^2$を定義するうえで分かりやすさを重視した結果語弊を生む可能性のあるものになってしまった. よって, これを解消するためにex:graphや図を載せたこれで理解してくれると幸いである.
他の定義と異なる場合があるが, それは有向グラフであったり多重グラフであったりを考えていることがある. また, 単に今回の趣旨とは外れるため定義を簡単にしたところがある. 詳しく知りたい方は調べてみると良い.
$V=\{1,2,3\}$とすると, その冪集合$\mathfrak{P}(V)$は$$\mathfrak{P}(V)=\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\}$$
である. $[V]^2$は
$$[V]^2=\{\{1,2\},\{1,3\},\{2,3\}\}$$
である.
即ち, $E$は$\{\{1,2\}\}$や$\{\{1,2\},\{1,3\}\}$や$\{\{1,2\},\{1,3\},\{2,3\}\}=[V]^2$などである.
(単純無向)グラフをわかりやすく図にしよう.
例えば頂点集合$V=\{a,b,c,d\}$,辺集合$E=\{\{a,b\},\{a,c\},\{a,d\},\{c,d\}\}$のとき, グラフ$G=(V,E)$は次のように図示できる.
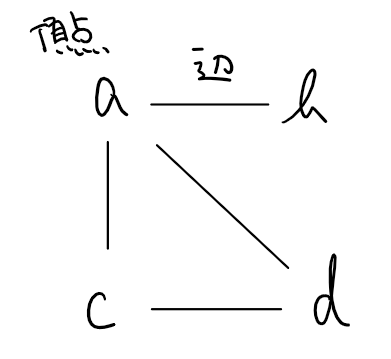
即ち, グラフ$G$の頂点を過不足なく書き, 辺に対応する線分を引く(つまり, 辺$\{a,b\}$に対して頂点$a,b$を繋げるように線分を引く).
グラフで距離を考える!!
さあ!この図を見たら「距離」を考えたくなるでしょう!!
グラフ理論の言葉での「距離」の定義は時期尚早である. (きちんとした定義はほかの記事で扱うことにする)
ではどのような「関数」を考えたら「距離の公理」を満たすことができるかを考察していこう.
次のグラフ$G$を考えよう.
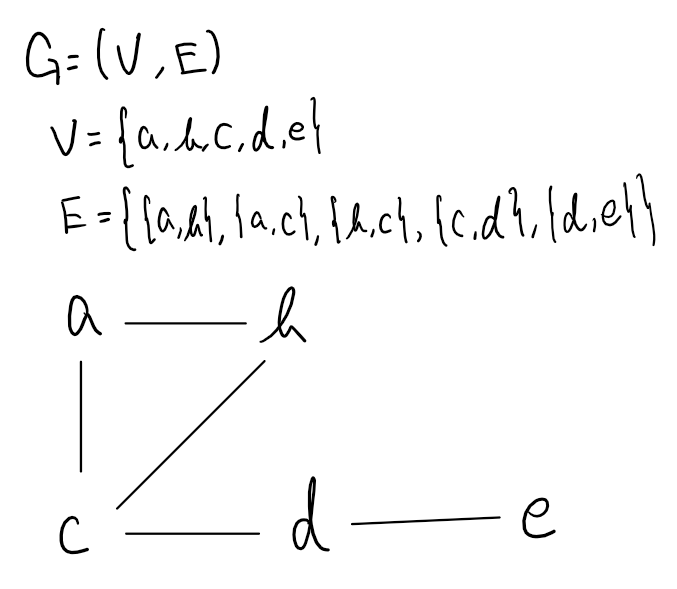
def:distanceを再掲しておく.
$X$を空でない集合とする. 関数$d:X\times X \rightarrow \mathbb{R}$が次の3つ条件を満たすとき, 関数$d$を集合$X$上の距離関数と呼ぶ.
任意の$x,y,z\in X$に対して
(1) $d(x,y) \ge 0$である. そして, $d(x,y) = 0 \Leftrightarrow x = y$.
(2) $d(x,y) = d(y,x)$.
(3) $d(x,z) \le d(x,y) + d(y,z)$.
さて, ここでの集合$X$は空でない集合である必要があった.
...! 頂点集合$V$は定義より空でなかった!!
そこで関数$d^{\dagger}:V\times V\rightarrow \mathbb{R}$を次のように考えてみるのはどうだろうか.
(上の例を用いた説明)
頂点$\alpha$と頂点$\beta$との「間」にある辺の数を「2つの頂点間の距離」$d^{\dagger}(\alpha,\beta)$とすると$d^{\dagger}$は距離の公理を満たす.
$d$と$e$の間にある辺の数は1なので$d^{\dagger}(d,e)=1$,$c$と$e$の間にある辺の数は2なので$d^{\dagger}(c,e)=2$である.
ふむ...これは「頂点間の離れ度合い」を表していているのかな...なら$d^{\dagger}$は距離関数といっても良さそう...?
Q. 本当にそうだろうか.
A. これは距離関数にはならないしそもそも関数ですらない.
$d^{\dagger}(b,c)$を考える. これはすぐに$d^{\dagger}(b,c)=1$だと言いたくなるが実際には$d^{\dagger}(b,c)=2$なども取りうることがわかる.
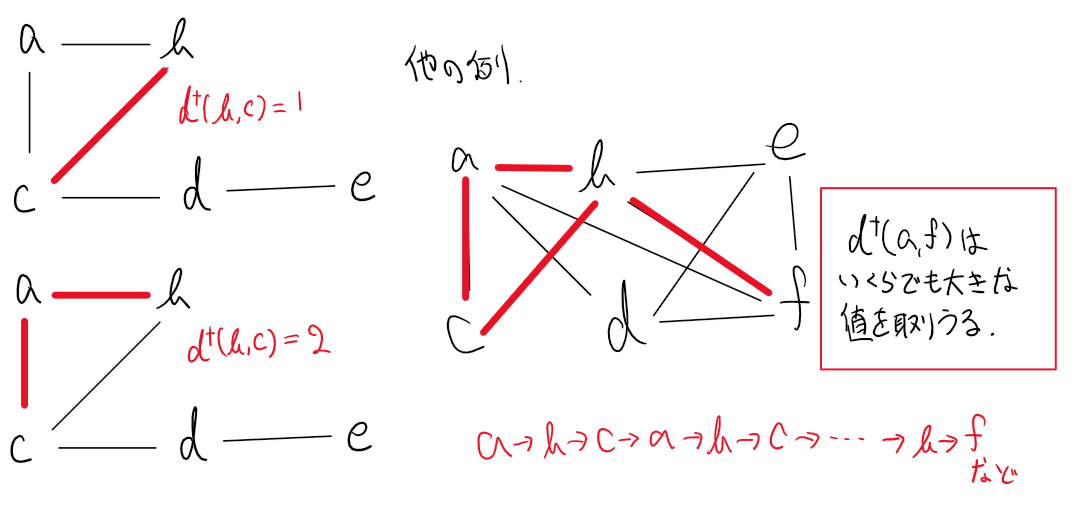
(違うグラフでの例も挙げた)
ここで問題になったのは, 頂点から頂点への経路が一意に定まらないので複数値が考えられることと, 同じところを繰り返すことで複数値が考えられることであった.
ではどうしたらよいだろうか...
以下の概念を用いて上で挙げた「他の例」のような状況を考えなくて済む.
すべての頂点が異なる経路を道という.
また, 複数の値をとることを解消するために道(経路)に含まれる辺の数(道(経路)の長さという)の最小値を考えてみる.
上の予想を改良して次の予想を立てる.
異なる2頂点$\alpha,\beta$を結ぶ道の長さの最小値を2頂点の距離と呼び$d^{\dagger}(\alpha,\beta)$と表せば$d^{\dagger}$は距離の公理を満たす.
それっぽくなってきたが$d^{\dagger}$は「距離の公理」を満たすのだろうか?
このままでは満たさないことは明らかである.
($\because $ $\alpha,\beta$が同じ頂点の場合に一切触れていないから)
異なる2頂点$\alpha,\beta$を結ぶ道の長さの最小値を2頂点の距離と呼び$d^{\dagger}(\alpha,\beta)$と表し, $\alpha=\beta$のとき$d^{\dagger}(\alpha,\beta)=0$と定める.このとき$d^{\dagger}$は距離の公理を満たす.
def:distanceを再再掲しておく.
$X$を空でない集合とする. 関数$d:X\times X \rightarrow \mathbb{R}$が次の3つ条件を満たすとき, 関数$d$を集合$X$上の距離関数と呼ぶ.
任意の$x,y,z\in X$に対して
(1) $d(x,y) \ge 0$である. そして, $d(x,y) = 0 \Leftrightarrow x = y$.
(2) $d(x,y) = d(y,x)$.
(3) $d(x,z) \le d(x,y) + d(y,z)$.
簡単な計算によって(1),(2),(3)が成り立つ...と思いきや一つ忘れていることがある.
ここでdef:graphに戻ろう.
気付いたであろうか?そう, グラフには以下のようなものも含まれるのである.
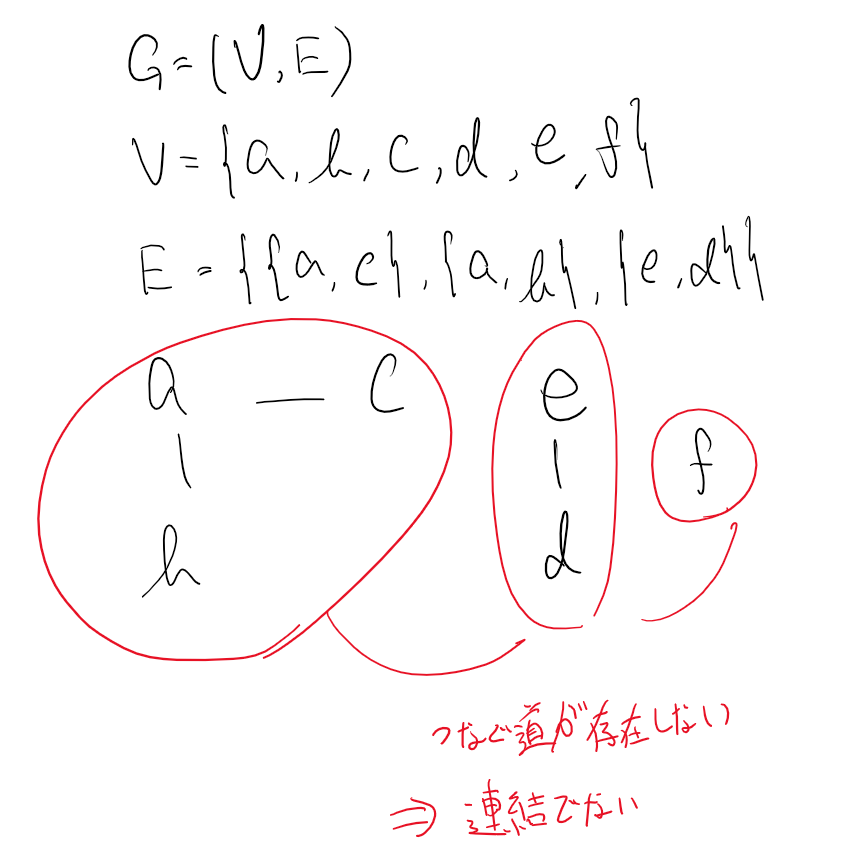
このようなグラフを連結でないグラフと呼ぶ.
この記事では便宜上, グラフの頂点間の距離を考えるときそのグラフは連結なグラフとする.
(例えば図5における$a,e$や$e,f$の距離を$d^{\dagger}(a,e)=\infty$とすることもあるがここでは扱わない)
グラフ$G$のどの異なる2頂点を選んでもそれらを結ぶ道が存在するとき$G$を連結なグラフであるという.
さあ, 予想の時間です.
連結なグラフ$G=(V,E)$に対して$V$上の関数$d^{\dagger}:V\times V\rightarrow\mathbb{R}$を次で定めると$d^{\dagger}$は距離関数となる.
$\alpha,\beta\in V$とし
$(\mathrm{I})$ $\alpha=\beta$のとき$d^{\dagger}(\alpha,\beta)=0$.
$(\mathrm{I\hspace{-1.2pt}I})$ $\alpha\ne \beta$のとき$\alpha,\beta$を結ぶ道の長さの最小値を$l$とすると$d^{\dagger}(\alpha,\beta)=l.$
つまり, この予想は関数$d^{\dagger}$を定義したときにそれが「距離の公理」を満たすかどうかを問うている.
予想1,2(2')はうまくいかなかったが, 予想3はうまくいくだろうか.
「三度目の正直」となるか, はたまた「二度あることは三度ある」のか, 「閲覧者の顔も三度」ここらで決着をつけたい.
Q. この予想は正しいか?
A. 正しい!
では証明してみよう.
def:distanceを再再再掲しておく. (もう覚えたかな?)
$X$を空でない集合とする. 関数$d:X\times X \rightarrow \mathbb{R}$が次の3つ条件を満たすとき, 関数$d$を集合$X$上の距離関数と呼ぶ.
任意の$x,y,z\in X$に対して
(1) $d(x,y) \ge 0$である. そして, $d(x,y) = 0 \Leftrightarrow x = y$.
(2) $d(x,y) = d(y,x)$.
(3) $d(x,z) \le d(x,y) + d(y,z)$.
(1),(2)は$d^{\dagger}$の定義から明らかであろう.
(3)
$(\mathrm{i})$
$x=z$のとき
$(\mathrm{I})$から$d^{\dagger}(x,z)=0$,$(1)$から$d^{\dagger}(x,y)\ge 0,d^{\dagger}(y,z)\ge0$より
$$
d^{\dagger}(x,z)=0\le d^{\dagger}(x,y)+d^{\dagger}(y,z).
$$
$(\mathrm{ii})$
$x\ne z$のとき
$\quad (a)$ $x=y$のとき
$$
d^{\dagger}(x,z)=d^{\dagger}(x,x)+d^{\dagger}(x,z)=d^{\dagger}(x,y)+d^{\dagger}(y,z).
$$
$\quad (b)$ $y = z$のとき
$$
d^{\dagger}(x,z)=d^{\dagger}(x,z)+d^{\dagger}(z,z)=d^{\dagger}(x,y)+d^{\dagger}(y,z).
$$
$\quad (c)$ $x\ne y,y\ne z$のとき
定義より
長さ$d^{\dagger}(x,y)$の道と, 長さ$d^{\dagger}(y,z)$の道が存在して, それらの道をつなぎ合わせることで長さ$d^{\dagger}(x,y)+d^{\dagger}(y,z)$の$x$と$z$の経路を作れる.
$x$と$z$の経路は$x$と$z$の道を含むので
$$
d^{\dagger}(x,z)\le d^{\dagger}(x,y)+d^{\dagger}(y,z).
$$
以上より, $d^{\dagger}$は距離の公理を満たし$V$上の距離関数となる.
終わりに
tea break が以外にも長くなったため今回はここで終わろうと思う.次回は距離空間の開集合や近傍, 連続について扱う.次々回で扱う位相空間の先駆けとして理解を確かなものにして欲しい.