Riemann-Siegelの積分公式とゼータ関数

はじめに

Riemann-Siegelの積分公式

(ただし、積分経路は0と1の間を通る傾き-1の直線を右へ進む。)

を示し、ゼータ関数の積分表示を導出します。

有用なのかは、、謎。

この記事は
Edwards, H.M. (1974), Riemann's zeta function, Pure and Applied Mathematics
の7.4、7.9を参考にしています

積分公式を示す

次の周回積分を考える
$\quad \dis\oint_{C}\frac{e^{-i\pi t^2+2i\pi tx}}{e^{i\pi t}-e^{-i\pi t}}dt$

ただし、経路$C=C_1+C_2+C_3+C_4$で、図のようにとる。ただし、$1< a\quad , \quad 0<\epsilon<1$

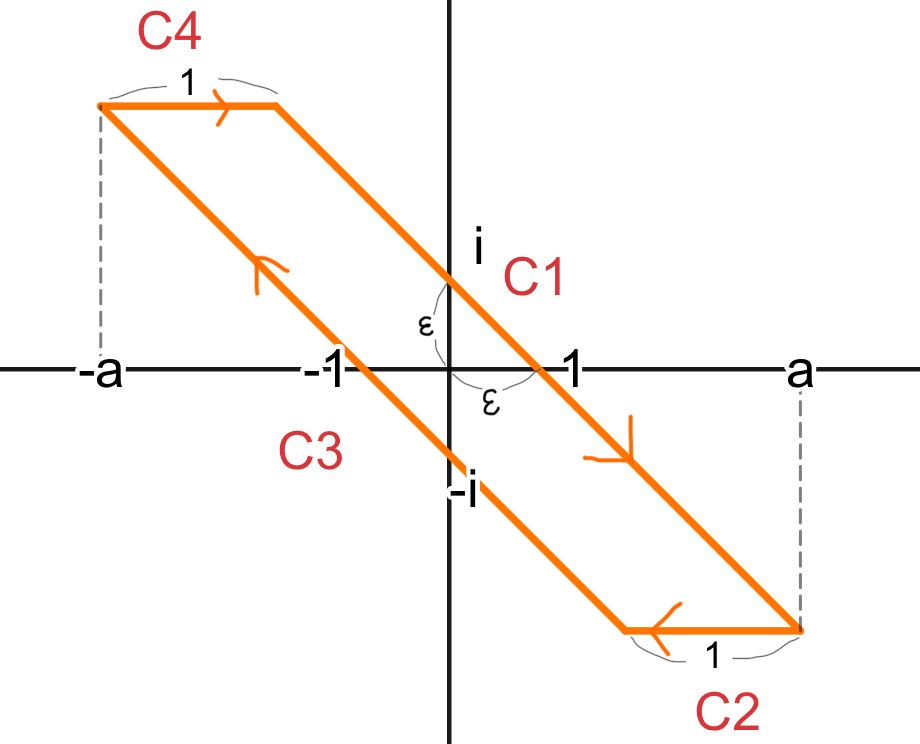
この積分結果は、被積分関数が$t=0$に一位の極を持つことから、留数定理を用いて$-1$となる。(割愛)

$C_1$と $C_3$

求めたいのは$a\to\infty$の$C_1$。
他と$C_1$の関係を見つける。

$C_3$の経路は、$C_1$の経路から、1引いたとこを通っている。(向きは逆)
なので、
$\quad \dis\int_{C_3}=-\int_{C_1}\frac{e^{-i\pi (t-1)^2+2i\pi x(t-1)}}{e^{i\pi(t-1)}-e^{-i\pi(t-1)}}dt$

変形すると、
$\quad \dis=-\int_{C_1}\frac{e^{-i\pi t^2+2i\pi t-i\pi+2i\pi xt-2i\pi x}}{e^{i\pi t-i\pi}-e^{-i\pi t+i\pi}}dt$

$\quad \dis=-e^{-2i\pi x}\int_{C_1}\frac{e^{-i\pi t^2+2i\pi (x+1)t}}{e^{i\pi t}-e^{-i\pi t}}dt$

これ積分は$x$を$x+1$に置き換えた時の$C_1$になっている。

ということで、
$\quad f(x)=\dis\int_{C_1}\frac{e^{-i\pi t^2+2i\pi tx}}{e^{i\pi t}-e^{-i\pi t}}dt$

としたとき、

$\quad \dis\int_{C_3}=-e^{-2i\pi x}f(x+1)$

である。 　　

$C_2$ と　$C_4$

$\dis\int_{C_2}\frac{e^{-i\pi(t^2-2tx)}}{e^{i\pi t}-e^{-i\pi t}}dt$

$a\to\infty$のとき、$C_2$上を動く$i\pi t^2$の実部が無限に大きくなる。
他の$t$が変数のとこは、$t^2$が強いので無視。
よって、被積分関数は0に近づいてく。

んで結局、$C_4$も$a\to\infty$で0になる。

漸化式

以上より、$a\to\infty$のとき、

$\quad f(x)-e^{-2i\pi x}f(x+1)=-1$

つまり

　
それと結局$f(x)$は求めたい積分、

$\quad f(x)=\dis\int_{0\searrow 1}\frac{e^{-i\pi t^2+2i\pi tx}}{e^{i\pi t}-e^{-i\pi t}}dt$

になっている。

まだこれだけでは$f(x)$は判明しない。

$f(x)$と$f(x+1)$

もう一本$f(x)$と$f(x+1)$の関係式を見つけたい。

気づきにくいけど、引くと約分できる。

$f(x+1)-f(x)=\dis\int_{0\searrow 1}\frac{e^{-i\pi t^2+2i\pi tx+2i\pi t}-e^{-i\pi t^2+2i\pi tx}}{e^{i\pi t}-e^{-i\pi t}}dt$

$\qquad=\dis\int_{0\searrow 1}\frac{e^{-i\pi t^2+2i\pi tx+i\pi t}(e^{i\pi t}-e^{-i\pi t})}{e^{i\pi t}-e^{-i\pi t}}dt$

$\qquad=\dis\int_{0\searrow 1}e^{-i\pi t^2+2i\pi t(x+\frac{1}{2})}dt$

変数変換$t=u+(\epsilon-u)i$

$\qquad=(1-i)\dis\int_{-\infty}^{\infty}e^{-i\pi (u+(\epsilon-u)i)^2+2i\pi(u+(\epsilon-u)i)(x+\frac{1}{2})}du$

$\qquad=(1-i)\dis\int_{-\infty}^{\infty}e^{-2\pi (u^2-\left(\epsilon+x+\frac{1}{2}+(-\epsilon+x+\frac{1}{2})i\right) u—i\frac{\epsilon^2}{2}+\epsilon(x+\frac{1}{2}))}du$

$\qquad=(1-i)e^{i\pi\epsilon^2-\pi\epsilon(2x+1)}\dis\int_{-\infty}^{\infty}e^{-2\pi (u^2-\left(\epsilon+x+\frac{1}{2}+(-\epsilon+x+\frac{1}{2})i\right) u)}du$

この積分は$\int_{-\infty}^{\infty}e^{-(x^2+sx)}dx$の形なので計算できる。
(複素数も混ざってるけど、ガウス関数のフーリエ変換とかの結果から(多分)いける。)

$\quad=\dis(1-i)e^{i\pi\epsilon^2-\pi\epsilon(2x+1)}\Bigg(\frac{1}{\sqrt{2}}e^{\pi(\epsilon(2x+1)+i(x+\frac{1}{2})^2-i\epsilon^2)}\Bigg)$

$\quad=\dis\frac{1-i}{\sqrt{2}}e^{i\pi(x+\frac{1}{2})^2}$

$\quad=\dis\frac{1-i}{\sqrt{2}}e^{\frac{i\pi}{4}}e^{i\pi(x^2+x)}$

$\quad=\dis e^{i\pi(x^2+x)}$

うまいこと色々消えてった。

完成！

よって、

これに
さっきの式

$\quad f(x+1)=\dis e^{2i\pi x}(f(x)+1)$

を代入すれば

$\quad \dis e^{2i\pi x}(f(x)+1)-f(x)=e^{i\pi x^2+i\pi x}$

解くと

$\quad \dis f(x)=\frac{e^{i\pi x^2+i\pi x}-e^{2i\pi x}}{e^{2i\pi x}-1}$

分子分母$e^{-i\pi x}$をかける

$\quad \dis f(x)=\frac{e^{i\pi x^2}-e^{i\pi x}}{e^{i\pi x}-e^{-i\pi x}}$

完成！

ゼータ関数との関係

以上の結果は、
$\quad \dis\int_{0\searrow 1}\frac{e^{-i\pi t^2+2i\pi tx}}{e^{i\pi t}-e^{-i\pi t}}dt=\frac{e^{i\pi x^2}}{e^{i\pi x}-e^{-i\pi x}}-\frac{1}{1-e^{-2i\pi x}}$
とも書ける。
そして、ゼータ関数の積分表示を知ってる人なら、右辺二項目に$x^{s-1}$を掛けて積分したすぎて堪らないと思う。そうしたらゼータ関数の表示が得られるのではないか。

と、いうことで両辺その通り積分。
ただし、都合があって、積分は$0$から$e^{\frac{i\pi}{4}}\infty$まで。(斜めに動くということ。この表記はなんか変な気もするけど。)

左辺

左辺はしれっと順序を入れ替えて、

$\quad \dis\int_{0}^{e^{\frac{i\pi}{4}}\infty}x^{s-1}\int_{0\searrow 1}\frac{e^{-i\pi t^2+2i\pi tx}}{e^{i\pi t}-e^{-i\pi t}}dtdx$

$\quad =\dis\int_{0\searrow 1}\frac{e^{-i\pi t^2}}{e^{i\pi t}-e^{-i\pi t}}\int_{0}^{e^{\frac{i\pi}{4}}\infty}x^{s-1}e^{2i\pi tx}dxdt$

$\quad =(-2i\pi)^{-s}\Gamma(s)\dis\int_{0\searrow 1}\frac{e^{-i\pi t^2}t^{-s}}{e^{i\pi t}-e^{-i\pi t}}dt$

左辺の変形はここまで。

右辺一項目

$\quad \dis\int_{0}^{e^{\frac{i\pi}{4}}\infty}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx$

天下り的だけど、次の積分を考える。

$\quad\dis\int_{0\nearrow 1}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx$

積分経路は0と1の間を通る傾き1の直線。

ここで、もし$2< s$なら、極が打ち消されます。よって、最初に示した積分のような$x=0$での留数は0となる。
ということは、積分経路は0を通る傾き1の直線としても、問題ない。
が、自分もよく分かってないので、完璧な説明は出来かねる。すみません。

では、変形してく

$\quad=\dis\int_{-e^{\frac{i\pi}{4}}\infty}^{e^{\frac{i\pi}{4}}\infty}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx$

$\quad=\dis\int_{-e^{\frac{i\pi}{4}}\infty}^{0}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx+\int_{0}^{e^{\frac{i\pi}{4}}\infty}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx$

$\quad=-\dis\int_{0}^{e^{\frac{i\pi}{4}\infty}}\frac{e^{i\pi x^2}(-x)^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx+\int_{0}^{e^{\frac{i\pi}{4}}\infty}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx$

$\quad=\dis\int_{0}^{e^{\frac{i\pi}{4}\infty}}\frac{e^{i\pi x^2}(x^{s-1}-(-x)^{s-1})}{e^{i\pi x}-e^{-i\pi x}}dx$

ここで、$u $を実数とすると$x=e^{\frac{i\pi}{4}}u$と、表される。このとき、$-x=e^{\frac{5i\pi}{4}}u$
となるが、主値をとると$-x=e^{\frac{-3i\pi}{4}}u$
よって$-x=e^{-i\pi}x$
ここの説明も何か腑に落ちないけど。

そうすると

$\quad=\dis\int_{0}^{e^{\frac{i\pi}{4}\infty}}\frac{e^{i\pi x^2}(x^{s-1}-e^{-i\pi(s-1)}x^{s-1})}{e^{i\pi x}-e^{-i\pi x}}dx$

$\quad=(1-e^{-i\pi(s-1)})\dis\int_{0}^{e^{\frac{i\pi}{4}\infty}}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx$

ということで、

$\quad\dis\int_{0}^{e^{\frac{i\pi}{4}\infty}}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx=\frac{1}{1-e^{-i\pi(s-1)}}\int_{0\nearrow 1}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx$

右辺ニ項目

$\quad\dis\int_{0}^{e^{\frac{i\pi}{4}}\infty}\frac{x^{s-1}}{1-e^{-2i\pi x}}dx$

$\quad=-\dis\int_{0}^{e^{\frac{i\pi}{4}}\infty}\sum_{k=1}^{\infty}e^{2i\pi x k}x^{s-1}dx$

$\quad=-\dis(-2i\pi)^{-s}\Gamma(s)\sum_{k=1}^{\infty}k^{-s}$

$\quad=-\dis(-2i\pi)^{-s}\Gamma(s)\zeta(s)$

きたーーゼータ関数だー

ゼータ関数の積分表示

以上を元の等式に適用すると

$\quad\dis(-2i\pi)^{-s}\Gamma(s)\int_{0\searrow 1}\frac{e^{-i\pi x^2}x^{-s}}{e^{i\pi x}-e^{-i\pi x}}dx=\frac{1}{1-e^{-i\pi(s-1)}}\int_{0\nearrow 1}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx+\dis(-2i\pi)^{-s}\Gamma(s)\zeta(s)$

これだけでもゼータ関数の表示となってる。
が、もう少し変形する。

両辺$(1-e^{-i\pi(s-1)})$を掛ける。
ここで、
$\,(1-e^{-i\pi(s-1)})(-i)^{-s}=-2\sin(\frac{\pi(s-1)}{2})$
となることに注意

$\quad\dis-2(2\pi)^{-s}\sin(\frac{\pi(s-1)}{2})\Gamma(s)\int_{0\searrow 1}\frac{e^{-i\pi x^2}x^{-s}}{e^{i\pi x}-e^{-i\pi x}}dx=\int_{0\nearrow 1}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx-2(2\pi)^{-s}\sin(\frac{\pi(s-1)}{2})\Gamma(s)\zeta(s)$ 　

今度は$\pi^{-\frac{1}{2}}\Gamma(\frac{1-s}{2})$を掛ける。

$\,\sin(\frac{\pi(s-1)}{2})\Gamma(s)\Gamma(\frac{1-s}{2})=-\sqrt{\pi}2^{s-1}\Gamma(\frac{s}{2})$
に注意する。

$\quad\dis\pi^{-s}\Gamma\left(\frac{s}{2}\right)\int_{0\searrow 1}\frac{e^{-i\pi x^2}x^{-s}}{e^{i\pi x}-e^{-i\pi x}}dx=\pi^{-\frac{1}{2}}\Gamma\left(\frac{1-s}{2}\right)\int_{0\nearrow 1}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx+\pi^{-s}\Gamma\left(\frac{s}{2}\right)\zeta(s)$

最後に$\pi^{\frac{s}{2}}$を掛ける

$\quad\dis\pi^{-\frac{s}{2}}\Gamma\left(\frac{s}{2}\right)\int_{0\searrow 1}\frac{e^{-i\pi x^2}x^{-s}}{e^{i\pi x}-e^{-i\pi x}}dx=\pi^{-\frac{1-s}{2}}\Gamma\left(\frac{1-s}{2}\right)\int_{0\nearrow 1}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx+\pi^{-\frac{s}{2}}\Gamma\left(\frac{s}{2}\right)\zeta(s)$ 　

ゼータ関数の項を持ってくると、

途中、$2< s$とか言ってたけど、上の式は負の偶数と0と正の奇数以外なら使える。

クシー関数の対称性

左辺をクシー関数

を使って書くと

$\dis\frac{2\xi(s)}{s(1-s)}=-\pi^{-\frac{s}{2}}\Gamma\left(\frac{s}{2}\right)\int_{0\searrow 1}\frac{e^{-i\pi x^2}x^{-s}}{e^{i\pi x}-e^{-i\pi x}}dx-\pi^{-\frac{1-s}{2}}\Gamma\left(\frac{1-s}{2}\right)\int_{0\nearrow 1}\frac{e^{i\pi x^2}x^{s-1}}{e^{i\pi x}-e^{-i\pi x}}dx$

なんか$s$と$1-s$ばっかだな、、ということで、

$F(x)=\dis-\pi^{-\frac{s}{2}}\Gamma\left(\frac{s}{2}\right)\int_{0\searrow 1}\frac{e^{-i\pi x^2}x^{-s}}{e^{i\pi x}-e^{-i\pi x}}dx$

としたとき、

らしい。(証明略)
なんともスッキリ。ここからクシー関数の関数等式が証明できる。なるほど。

感想

最後にかけて、適当っぽくなってすみません。
$e^{-i\pi(ax^2+2bx)}$の形が便利すぎる。
今回の$f(x)$ぼ漸化式もほぼこれによるものだし、積分も出来ちゃって、複素共役にも良いっぽい。
今回の話からはそれるが、楕円テータ関数もこの形がいい仕事してる。
擬二重周期が得られて、無限積表示、モジュラー変換式に繋がってく。

なんかまだ何かできそうな雰囲気があるなぁ。。

ここまで。間違いあれば指摘ください