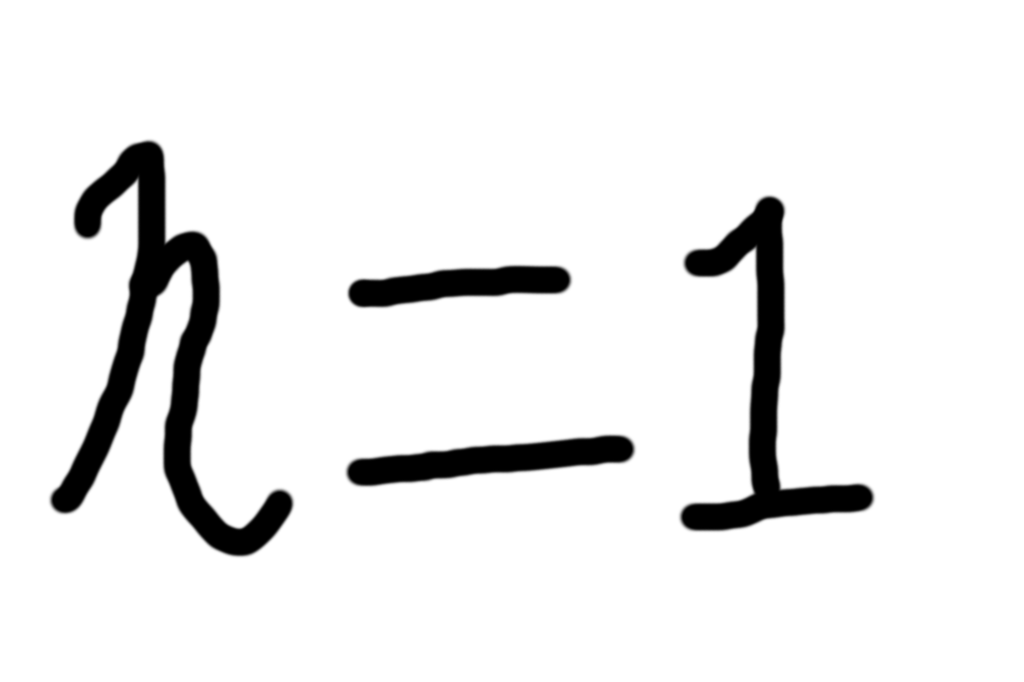循環しない規則的な小数

はじめに

　こんにちはn=1です。
　今回は、循環小数を計算してるときに思いついた規則的かつ循環していない小数の少しの例を書いていきます。

例

　では一つ目の例の$0.1010010001000010\cdots$を求めます。これは$\sum_{k=1}^{∞}10^{-f(k)}$で求められそうです。$f(k)$は1が出る順番の式を求めれば良いので、 前回の記事 の式を使い、
$a_{n}=${$1,3,6,(10,15,)\cdots$}
$a_{n}=\frac{(-1)^{1-3}}{(1-1)!(3-1)!}(n-2)(n-3)+\frac{(-1)^{2-3}3}{(2-1)!(3-2)!}(n-1)(n-3)+\frac{(-1)^{3-3}6}{(3-1)!(3-3)!}(n-1)(n-2)=\frac{1}{2}n^{2}+\frac{1}{2}n$
これを上記に代入し
$0.101001001000010\cdots=\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k}$
と分かります。
　次に、2つめの例は$0.10110111011110\cdots$です。一つ目の式を0と1の個数を入れ替えただけですが、これでは先の解法は使えません。では解いていきましょう。この数は$0.111\cdots(\frac{1}{9})$に近いのでそこから引き算で表そうとすると$0.10110111011110\cdots=0.11111111111111\cdots-0.01001000100001\cdots=\frac{1}{9}-(-1+10{(例1の式)})$
とでき、$\frac{1}{9}=\sum_{k=1}^{∞}10^{-k}$、例1と同じように規則性を見つけ$0.01001\cdots=\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{3}{2}k}$となるので答えは
$\frac{10}{9}-10\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k}=\sum_{k=1}^{∞}10^{-k}-10^{-\frac{1}{2}k^2-\frac{3}{2}k}$
です。
　最後、三つ目の例は、$0.248163264128256\cdots$で、2の冪乗が順にある数です。これは$\sum_{k=1}^{∞}10^{-f(k)}2^k$で表せそうなのでまた$f(k)$を求めれば良いです。$f(x)$は$x$がありそこから桁数-1を足せば正しい式になりそうでそれは2桁以上は全て足されていて、これを式にし
$0.24816326428256\cdots=\sum_{k=1}^{∞}10^{-k-\sum_{m=1}^{k}⌊m\log_{10}2⌋}2^{k}$
が答えです。

例題

↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
　以下は解説です。
　問1の回答は$0.0111011110111110\cdots+0.001000010000010\cdots$の二つで表せるので、それぞれを求め、
$0.0111011110111110\cdots=-1011+10^{4}(\frac{10}{9}-10\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k})=\frac{10^{5}-9099}{9}-10^{5}\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k}$
$0.001000010000010\cdots=-1010010+10^{7}\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k}$
なので合わせて
$0.0121011210111210\cdots=\frac{10^{5}-9099}{9}-1010010-10^{5}\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k}+10^{7}\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k}=-\frac{8999189}{9}+99000000\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k}$
が答えです。
　問2の答えは、$0.222\cdots$を基準に$0.0121011210111210\cdots$を足しているので問1の解と足して解は
$-\frac{8999187}{9}+9900000\sum_{k=1}^{∞}10^{-\frac{1}{2}k^2-\frac{1}{2}k}$
です。
　問3の答えは、例3の様に
$0.1234567891011\cdots=\sum_{k=1}^{∞}10^{-k-\sum_{m=1}^{k}⌊\log_{10}m⌋}k$
となります。
　問4の答えは例2の$0.101101110\cdots$から0をいくつか増やしたものなので、例2の桁ごとに出力できる$F(k)$を使いいくつか10のマイナス乗をかければ良いと分かります。また、 前回の記事 の式をまた使い、$x^2-x+1$周期で初めの1が来ると分かり、そこから始まりを含め$x$回1が続くので、解は
$0.10110011100011110\cdots=\sum_{k=1}^{∞}10^{-k+1}\sum_{n=k^2-k+1}^{k^2+k}10^{F(n)}$
となります。

最後に

　以上で循環しない規則的な小数の内容は終わりです。少し長かったと思いますが、投稿を見てくださりありがとうございました。