ライツアウトの〇〇的解法
ライツアウトの代数的腕力的解法
はじめまして
こんにちは!はじめまして!しんぎゅらです🙇
数学垢を作ったのでMathlogも作ってみました。 記念すべき第1投稿目はパズル問題「ライツアウト」です。
これはとある""数理に興味のある中高生に数学の話をする某NPO団体""でスタッフとして発表したことのあるテーマを使い回します。
ライツアウトって何??
ライツアウトは、5×5の形に並んだライトをある法則にしたがってすべて消灯 (lights out) させることを目的としたパズル。
ルール
・あるライトを押すと、自身とその上下左右最大4個のライトが一緒に反転する。
・基本は5×5=25個の、光が点灯・消灯するボタンからなる。 問題がライトのパターンとして出される。解答者は上のルールに従って明滅するライトを操作し、最終的に全てのライトを消すことができれば勝ちとなる。一般に一つの問題に対し複数の解答があるため、最短手数の解答を競う。
引用:最近寄付の催促が激しいwikipedeia
https://ja.wikipedia.org/wiki/%E3%83%A9%E3%82%A4%E3%83%84%E3%82%A2%E3%82%A6%E3%83%88
要は押したボタンとその周りの色が変わるから、適当に押して全ボタンの色を変えてねってことですね!!
ライツアウトが遊べるURLを貼っておきますので、遊びたい方は是非!!
https://bubudoufu.com/webapp/lights-out/
今回は面倒(←怠惰)なのでの$ 3\times 3$ライツアウトを解こうと思います!!下の図は$ 3\times 3$のライツアウトで真ん中のボタンを押した時の図。
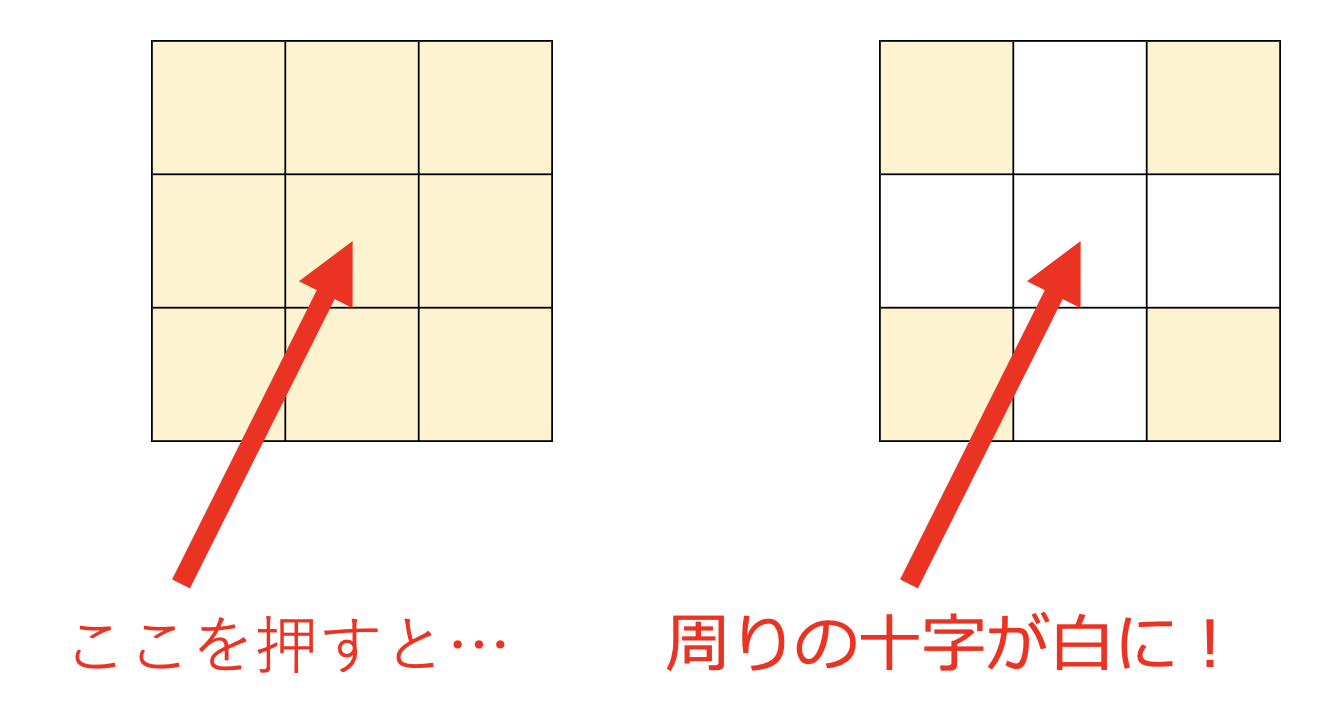 ライツアウト
ライツアウト
$ 3 \times 3$までならテキトーにポチポチしてれば、いつの間にかクリアしてることが多いですね。高々$2^{9}=512$通りポチればクリアなので是非暇人はこのページを閉じて気合いでやってみてください!!
暇人じゃない方、ようこそ
さて、暇人ではない方に朗報です!!これから私たちは9元連立方程式を解きます!!
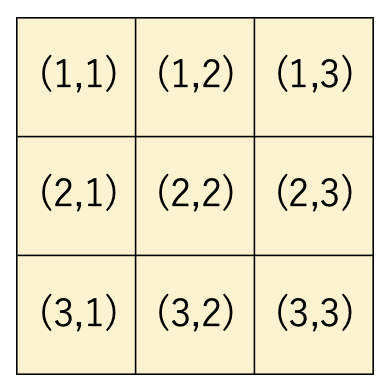
便宜上
・上から$i$行目、左から$j$行目のボタンを$(i,j)$成分
・$(1,1)$成分のような角のことをコーナー
・$(1,2)$成分のような縁のことをエッジ
・$(2,2)$成分のような角のことをセンター
と呼ぶことにします
アイデア
ボタンは押すか押さないかの2択で、さらに2回押すと元に戻ることに注意する。あ、お気付きですか?
そうです!!$1 + 1=0$の世界を考えれば良さそう!
押す操作を$+1$として考える。元々の状態を$0$、ライトが消えた状態を$1$とすれば、
・押す順番は結果に影響しない
・1回ボタンを押す操作で$0+1=1$つまりライトが消える
・もう1回ボタンを押すと$1+1=0$つまりライトがまたつく
確かに$1+1=0$の世界を考えるのが良さそう!!この世界を標数2の体$ \mathbb{F}_2 $と言います。
立式
さて、では$3\times 3$のライツアウトを解いていきましょう
元々の状態は$\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0
\end{array}
\right)
\end{eqnarray}$と思えますね
では$(1,1)$成分をポチったらどうなるでしょうか?
 元々の状態
から
元々の状態
から
![!FORMULA[21][-1217828083][0]成分を押された状態](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F2Uly1agyNwxfjXIiT5N2.png?alt=media) $(1,1)$成分を押された状態
になりますよね
$(1,1)$成分を押された状態
になりますよね
行列でいうと$\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0
\end{array}
\right)
\end{eqnarray}$から$\begin{eqnarray}
\left(
\begin{array}{cc}
1 & 1 & 0\\
1 & 0 & 0\\
0 & 0 & 0
\end{array}
\right)
\end{eqnarray}$になったわけです。これは単純に$\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0
\end{array}
\right)+
\left(
\begin{array}{cc}
1 & 1 & 0\\
1 & 0 & 0\\
0 & 0 & 0
\end{array}
\right)=
\left(
\begin{array}{cc}
1 & 1 & 0\\
1 & 0 & 0\\
0 & 0 & 0
\end{array}
\right)
\end{eqnarray}$というただの行列の足し算の結果ですね。
同様に$(1,2)$成分を押すときは$\begin{eqnarray}
\left(
\begin{array}{cc}
1 & 1 & 1\\
0 & 1 & 0\\
0 & 0 & 0
\end{array}
\right)
\end{eqnarray}$で、$(2,2)$成分を押すときは$\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 1 & 0\\
1 & 1 & 1\\
0 & 1 & 0
\end{array}
\right)
\end{eqnarray}$を足すという操作になりますね!!
では$(i,j)$成分を$x_{ij}$回押したとしましょう。このとき、
$\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0
\end{array}
\right)+x_{11}
\left(
\begin{array}{cc}
1 & 1 & 0\\
1 & 0 & 0\\
0 & 0 & 0
\end{array}
\right)+x_{12}
\left(
\begin{array}{cc}
1 & 1 & 1\\
0 & 1 & 0\\
0 & 0 & 0
\end{array}
\right)+x_{13}
\left(
\begin{array}{cc}
0 & 1 & 1\\
0 & 0 & 1\\
0 & 0 & 0
\end{array}
\right)+x_{21}
\left(
\begin{array}{cc}
1 & 0 & 0\\
1 & 1 & 0\\
1 & 0 & 0
\end{array}
\right)+x_{22}
\left(
\begin{array}{cc}
0 & 1 & 0\\
1 & 1 & 1\\
0 & 1 & 0
\end{array}
\right)+x_{23}
\left(
\begin{array}{cc}
0 & 0 & 1\\
0 & 1 & 1\\
0 & 0 & 1
\end{array}
\right)+x_{31}
\left(
\begin{array}{cc}
0 & 0 & 0\\
1 & 0 & 0\\
1 & 1 & 0
\end{array}
\right)+x_{32}
\left(
\begin{array}{cc}
0 & 0 & 0\\
0 & 1 & 0\\
1 & 1 & 1
\end{array}
\right)+x_{33}
\left(
\begin{array}{cc}
0 & 0 & 0\\
0 & 0 & 1\\
0 & 1 & 1
\end{array}
\right)=
\left(
\begin{array}{cc}
1 & 1 & 1\\
1 & 1 & 1\\
1 & 1 & 1
\end{array}
\right)
\end{eqnarray}$という式を満たす$x_{11}, \cdots ,x_{33}$の組みを考えれば良さそうですね!!(狂気)
左辺を一つの行列に収めると、$\begin{eqnarray}
\left(
\begin{array}{cc}
x_{11}+x_{12}+x_{21} & x_{11}+x_{12}+x_{13}+x_{22} & x_{12}+x_{13}+x_{23}\\
x_{11}+x_{21}+x_{22}+x_{31} & x_{12}+x_{21}+x_{22}+x_{23}+x_{32} & x_{13}+x_{22}+x_{23}+x_{33}\\
x_{21}+x_{31}+x_{32} & x_{22}+x_{31}+x_{32}+x_{33} & x_{23}+x_{32}+x_{33}
\end{array}
\right)=
\left(
\begin{array}{cc}
1 & 1 & 1\\
1 & 1 & 1\\
1 & 1 & 1
\end{array}
\right)
\end{eqnarray}$
ここで、成分ごとに式を立てると$\begin{eqnarray}
\left\{
\begin{array}{l}
x_{11}+x_{12}+x_{21}&=&1 \cdots (1) \\
x_{11}+x_{12}+x_{13}+x_{22}&=&1\cdots (2)\\
x_{12}+x_{13}+x_{23}&=&1 \cdots (3)\\
x_{11}+x_{21}+x_{22}+x_{31}&=&1 \cdots (4)\\
x_{12}+x_{21}+x_{22}+x_{23}+x_{32}&=&1 \cdots (5)\\
x_{13}+x_{22}+x_{23}+x_{33}&=&1 \cdots (6)\\
x_{21}+x_{31}+x_{32}&=&1 \cdots (7)\\
x_{22}+x_{31}+x_{32}+x_{33}&=&1 \cdots (8)\\
x_{23}+x_{32}+x_{33}&=&1 \cdots (9)
\end{array}
\right.
\end{eqnarray}$
という9元連立方程式が立てられますね!!(消え去った正気)
ゴリ押し計算
コツは$1+1=0$の性質を使うこと。
特に$x+x=(1+1)x=0$つまり同じものを2回足せば$0$なので、簡単に計算できそうですね !!
手元に↓こういう図を置いておくと、どこを計算してるのかが追えて分かりやすいと思います!!
 こういうの
こういうの
・$(1)+ \cdots+(9)$を計算
$(x_{11}+x_{12}+x_{21})+(x_{11}+x_{12}+x_{13}+x_{22})+(x_{12}+x_{13}+x_{23})+(x_{11}+x_{21}+x_{22}+x_{31})+(x_{12}+x_{21}+x_{22}+x_{23}+x_{32})+(x_{13}+x_{22}+x_{23}+x_{33})+(x_{21}+x_{31}+x_{32})+(x_{22}+x_{31}+x_{32}+x_{33})+(x_{23}+x_{32}+x_{33})=1+1+1+1+1+1+1+1+1$
同じ数同士整理してあげると...
$(x_{11}+x_{11}+x_{11})+(x_{12}+x_{12}+x_{12}+x_{12})+(x_{13}+x_{13}+x_{13})+(x_{21}+x_{21}+x_{21}+x_{21})+(x_{22}+x_{22}+x_{22}+x_{22}+x_{22})+(x_{23}+x_{23}+x_{23}+x_{23})+(x_{31}+x_{31}+x_{31})+(x_{32}+x_{32}+x_{32}+x_{32})+(x_{33}+x_{33}+x_{33})=1+1+1+1+1+1+1+1+1$
今、注意したいのは$1+1=0$なので同じ数は偶数回足すと$0$にしなります!!
故に$x_{11}$のようなコーナーの数は3回、$x_{12}$のようなエッジの数は4回、$x_{22}$のようなセンターの数は5回は足されているので、
$x_{11}+x_{13}+x_{22}+x_{31}+x_{33}=1\cdots (10)$になります。こう見るとかなり見通しが良くなった気がします。
・対角を計算
$(1)+(5)+(9)$を先ほどと同様に計算すると
$x_{11}+x_{22}+x_{33}=1\cdots (11)$と分かります。
$(3)+(5)+(7)$も計算すると
$x_{13}+x_{22}+x_{31}=1\cdots (12)$になります。
・あとはひたすら文字を消去
$(10)+(11)$を計算すると
$(x_{11}+x_{13}+x_{22}+x_{31}+x_{33})+(x_{11}+x_{22}+x_{33})=1+1$
$x_{11},x_{22,}x_{33}$が2回ずつ足されているので、消えて
$x_{13}+x_{31}=0\cdots (13)$
さぁ、ここでやっと1文字が解けます
$(12)+(13)$より
$(x_{13}+x_{22}+x_{31})+(x_{13}+x_{31})=1+0$
$\therefore x_{22}=1$
・まだまだ計算は続く
$(1)+(2)$より
$x_{21}+x_{13}+x_{22}=0$
$x_{22}=1$ゆえ$x_{21}+x_{13}=1\cdots(14)$
同様にして$(7)+(8)$より
$x_{21}+x_{22}+x_{33}=0$
$x_{22}=1$ゆえ$x_{21}+x_{33}=1\cdots(15)$
得られた$(14)$と$(15)$を足して
$x_{13}+x_{21}+x_{21}+x_{33}=0$
$\therefore x_{13}=x_{33}\cdots(16)$
・嬉しい瞬間
$(6)$について$(16)$の$x_{13}=x_{33}$と$x_{22}=1$より
$x_{23}=0$
やばい、気持ちぃぇぇええ!!!!
・まだまだ続く気持ち良いのフルコンボ
$(2)+(3)$より
$(x_{11}+x_{12}+x_{13}+x_{22})+(x_{12}+x_{13}+x_{23})=1+1$
$\therefore x_{11}+x_{22}+x_{23}=0$
$x_{22}=1,x_{23}=0$より
$x_{11}=1$
・やばい気持ち良すぎて手が止まんない
上と同じようにして
$(8)+(9)$より
$(x_{22}+x_{31}+x_{32}+x_{33})+(x_{23}+x_{32}+x_{33})=1+1$
$\therefore x_{22}+x_{31}+x_{23}=0$
$x_{22}=1,x_{23}=0$より
$x_{31}=1$
$(4)$より$x_{21}=0$
$(14),(15)$について
それぞれ$x_{13}+x_{21}=1,x_{21}+x_{33}=1$に$x_{21}=0$を使うと
$x_{13}=1,x_{33}=1$
$(1),(9)$について
それぞれ$x_{11}+x_{12}+x_{21}=1$と$x_{23}+x_{32}+x_{33}=1$に今までの結果を使うと
$x_{12}=0,x_{32}=0$
・そして感動のグランドフィナーレへ...
以上の計算により
$\begin{eqnarray}
\left\{
\begin{array}{l}
x_{11}=1 \\ x_{12}=0 \\
x_{13}=1 \\
x_{21}=0 \\ x_{22}=1 \\
x_{23}=0 \\
x_{31}=1 \\ x_{32}=0 \\
x_{33}=1 \\
\end{array}
\right.
\end{eqnarray}$
ふぅ〜...
実際に解いてみると...?
今の結果で本当にライツアウトが解けちゃうのか、気になりますよね?
$(1,1)$成分
↓
$(1,3)$成分
↓
$(2,2)$成分
↓
$(3,1)$成分
↓
$(3,3)$成分
の順番で押してみると...
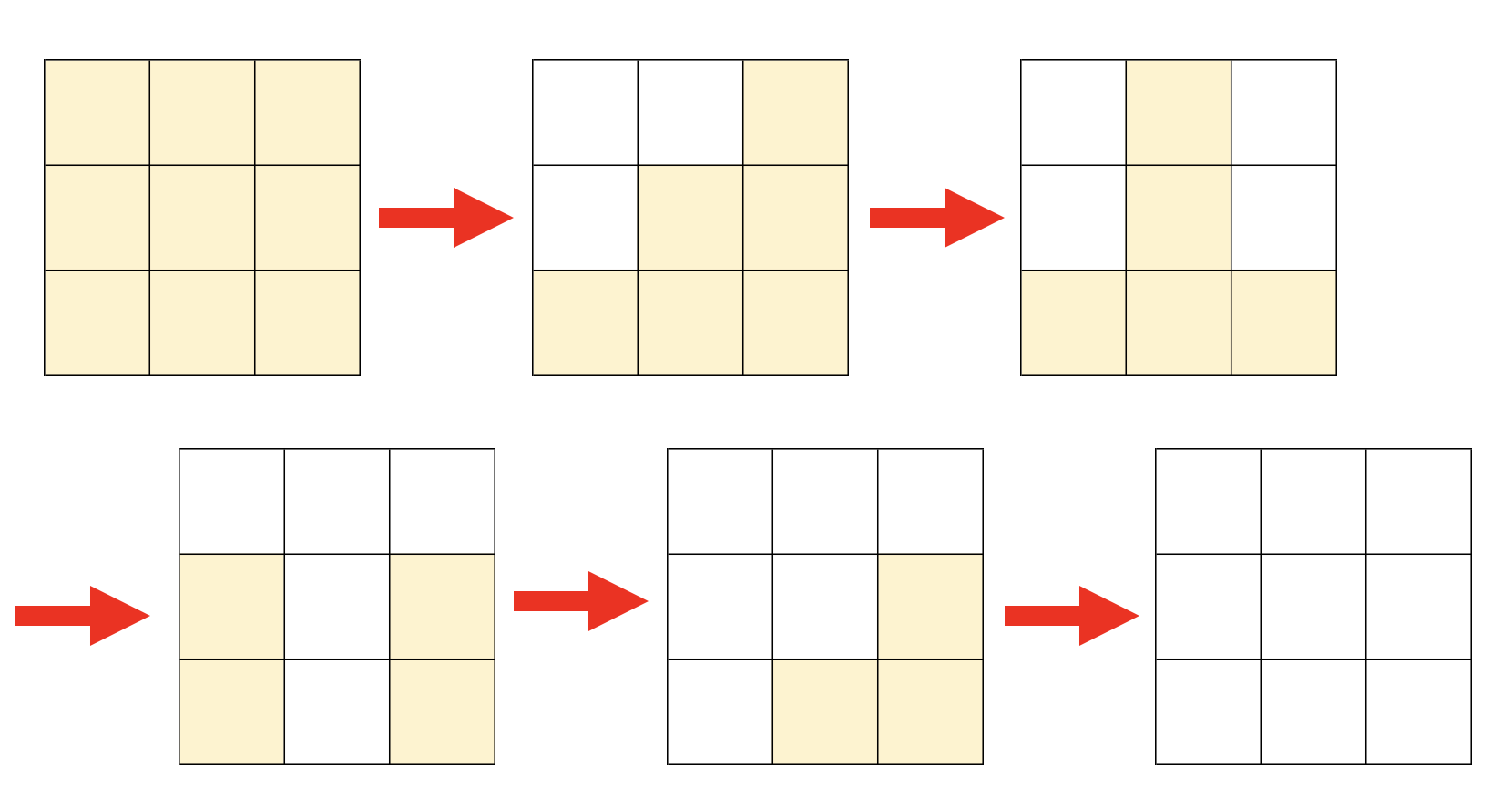 マジで解けてる
マジで解けてる
まとめ
以上のように$\mathbb{F}_{2}$を使って上手いこと解く方法があるのが分かって貰えたと思います。どこかの噂では嘘つき問題を$\mathbb{F}_{2}$で解けるとか解けないとか...
さて代数的に腕力的に解いていきましたが、このような連立方程式を解くのに便利な道具があるのも、ご存じですか?そうです、ポン酢がよく合うアレです。私がRisa/Asirを使いこなせるようになったら、更新するつもりです。皆さんもパズルを別のルートで解いてみるのはいかがでしょう?
それでは、さようなら!!👋
