コラッツ予想について考えたこと(追加)
前回、前々回の投稿に、コラッツ予想について思いついたことを記録しました。
それでおしまいにしようと思ったのですが、ぼんやりと思い浮かんだことがあるので追加します。厳密な証明はしていません。
結論
よくわからない議論が続くと思うので、結論から書きます。
$f: \mathbb{N} \Rightarrow \mathbb{N}$を以下で定義する。
$f(1)=2$.
$n \geq 2$に対して
$f(n)= \begin{eqnarray}
\left\{
\begin{array}{l}
\frac{2n}{3} \ (n \equiv 0 \mod 6 ) \\
\frac{4n-1}{3} \ (n \equiv 1 \mod 6 ) \\
\frac{8n-1}{3} \ (n \equiv 2 \mod 6 )\\
\frac{16n-9}{3} \ (n \equiv 3 \mod 6 )\\
\frac{2n+1}{3} \ (n \equiv 4 \mod 6 )\\
\frac{4n-2}{3} \ (n \equiv 5 \mod 6 )
\end{array}
\right.
\end{eqnarray} $
$ \forall n \in \mathbb{N} $に対し
$f(n)$の6による剰余は以下の確率をとる。
$0$または$2$または$4$となる確率$=$それぞれ $\frac{2}{18}$
$1$または$3$または$5$となる確率$=$それぞれ $\frac{4}{18}$
確率予想が成立する$\Leftrightarrow$ コラッツ数列は発散しない
説明
思いついたことのメモ書きです。
$g: \mathbb{N} \setminus \{1\} \Rightarrow \mathbb{N}$を以下で定義する。
$g(n)= \begin{eqnarray} \left\{ \begin{array}{l} 16n-3 \ (n\equiv 0 \mod 2 ) \\ 4n-2 \ (n\equiv 1 \mod 2 ) \end{array} \right. \end{eqnarray} $
$1$に$f$,$g$を適当に適用することで、任意の自然数を得る
$\Leftrightarrow$
コラッツ予想が成立する
↑これは 前回 説明しました。
$f$,$g$を図示すると以下のようなツリーになります。
$f$を適用すると下に移動します。($18 \rightarrow 12 \rightarrow 8$)
$g$を適用すると右に移動します。($8 \rightarrow 125 \rightarrow 498$)
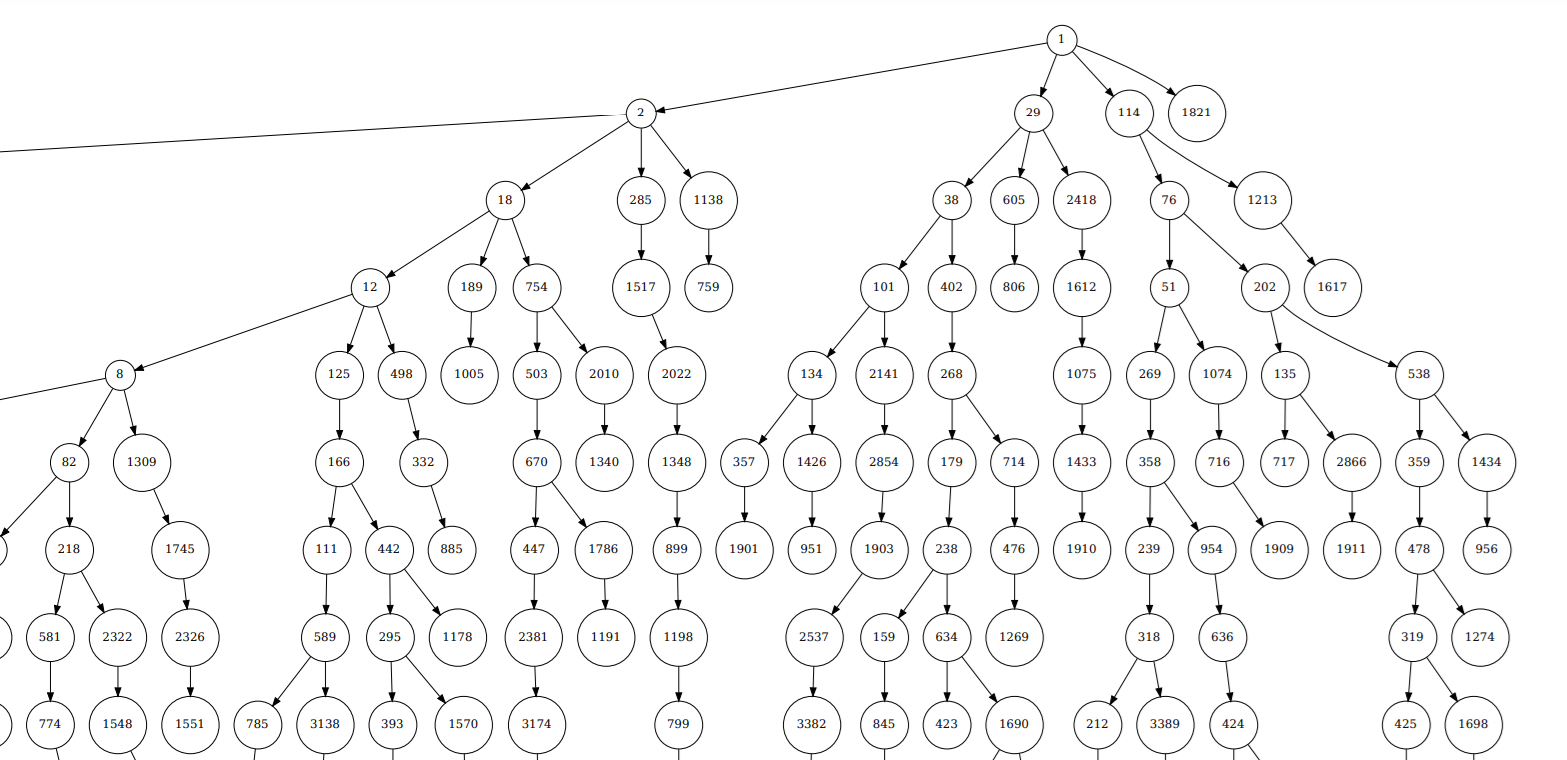 ツリー
ツリー
$1$をルートとするこのツリー上に全ての自然数が現れる、というのがコラッツ予想の主張です(たぶん)。
例を挙げます。
$8=f \cdot f \cdot g \cdot f \cdot f(1)$
$876=g \cdot f \cdot f \cdot g \cdot f \cdot f \cdot f \cdot f(1)$
逆に言うと、任意の数から$f^{-1}$, $g^{-1}$を辿ってツリーの上に昇っていくと、やがて$1$に到達するだろう、ということです。
反例があるとすると
さて、ではコラッツ予想が成立しないとしたらどうなるでしょうか。
その場合は、このツリーの他にツリーが存在することになります。
そのツリーの形は次の2種類が考えられます。
- 上方向、左方向に無限に広がる
- 上方向には無限に続くが、左側はある時点で止まる
$f^{-1}$, $g^{-1}$で昇って行ってもきりがない、ということですが
(1)の場合は昇る最中に$g^{-1}$がいつまでも出続けます。
(2)の場合は、あるところから$f^{-1}$のみとなります。
(1)がありえないことの証明のようなもの
(2025/03/16追記 ↓この証明は誤りです)直感的に(1)はありえないのではないか、と思います。
ちょっとあやしいですが以下の証明を考えました。
(1)の形のツリーが存在すると仮定する。
$ \exists n \in \mathbb{N} $に対し、無限に続く$f$, $g$の列が考えられる。
例えば
$n = f \cdot f \cdot g \cdot f \cdot f \cdot g \cdot g \cdot g \cdots $
(ツリーを遡っていく道筋に相当)
いま、$f$, $g$を並べた文字列を考え、$n$に対応させる。
$n:ffgffggg \cdots $
$f$を$1$, $g$を$0$と書き換え、先頭に「$0.$」を付けると、$ \exists r \in \mathbb{R}; \ 0 \lt r \leq 1 $の2進表示を得る。
$n:r=0.11011000 \cdots $
もとの$f$, $g$の列はあらゆる組み合わせをとるので、このようにして得られる$r$は$(0, 1] $区間の任意の実数を表現し得る。
したがって自然数$n$と実数$r$に「多:1」の対応を付けられることになり、不合理。
よって(1)の形のツリーは存在しない。
ツリーを遡る道筋と実数が対応付けられてしまうのでありえない、ということです。
(2025/03/16追記 ↑この証明は誤りです)
(2)の場合を考察
(2)の場合は、どの数列も遡っていく途中で必ずある数列に行き当たります。
ツリーの「一番左側」の数列です。
一番左側の数列は$f$のみで生成されています。
つまり、いろいろ書きましたが、結局$f$の振る舞いを調べれば十分だという事です。
コラッツ数列に立ち返って考えると、
(1)コラッツ数列がループする場合は「$4n+1$」の形の数は現れない
(2)コラッツ数列が発散する場合は、ある時点から「$4n+1$」を含まない数列になる
という訳です。
発散することはあるのか
ループの有無については全く考えが進まないので、発散する場合について考えます。
あらためて$f$について考察します。
$f(n)= \begin{eqnarray} \left\{ \begin{array}{l} \frac{2n}{3} \ (n \equiv 0 \mod 6 ) \\ \frac{4n-1}{3} \ (n \equiv 1 \mod 6 ) \\ \frac{8n-1}{3} \ (n \equiv 2 \mod 6 )\\ \frac{16n-9}{3} \ (n \equiv 3 \mod 6 )\\ \frac{2n+1}{3} \ (n \equiv 4 \mod 6 )\\ \frac{4n-2}{3} \ (n \equiv 5 \mod 6 ) \end{array} \right. \end{eqnarray} $
(以下、合同式はすべて$ \mod 6$で考えます)
コラッツ数列が発散するということは、$f^{-1}$が発散するという事です。
逆に$f$が「どんどん大きく」なればコラッツ数列が発散しないことになります。
確率を考えてみます
$f$が減少するのは $n \equiv 0 , 4$のときです。
$f$が十分多く繰り返されたときに、$n \equiv 0~5$の場合が同程度あらわれると仮定します。
$n$が大きければ$f$は以下の値で近似できます。
$f(n)\fallingdotseq \begin{eqnarray} \left\{ \begin{array}{l} \frac{2}{3} \ (n \equiv 0) \\ \frac{4}{3} \ (n \equiv 1) \\ \frac{8}{3} \ (n \equiv 2 )\\ \frac{16}{3} \ (n \equiv 3)\\ \frac{2}{3} \ (n \equiv 4)\\ \frac{4}{3} \ (n \equiv 5) \end{array} \right. \end{eqnarray} $
$f$の期待値を計算すると$2$になります。
つまり、$f$は指数関数的に増加していくことになります。
もう少し詳しく考えると、例えば$n \equiv 0$となる場合、$f(n) \equiv 0, 2, 4$に限定されます。(単純に計算すれば分かります)
つまり、$f$について$6$つの場合分けを考えるのではなく、以下の$18$通りの場合を考えることができます。
$n \equiv 0 \rightarrow \ f(n) \equiv 0, 2, 4$
$n \equiv 1 \rightarrow \ f(n) \equiv 1, 3, 5$
$n \equiv 2 \rightarrow \ f(n) \equiv 1, 3, 5$
$n \equiv 3 \rightarrow \ f(n) \equiv 1, 3, 5$
$n \equiv 4 \rightarrow \ f(n) \equiv 1, 3, 5$
$n \equiv 5 \rightarrow \ f(n) \equiv 0, 2, 4$
これらが同程度あらわれると仮定すると、$f(n)$の$6$による剰余は以下の確率をとることになります。
$0$または$2$または$4$となる確率$=$それぞれ $\frac{2}{18}$
$1$または$3$または$5$となる確率$=$それぞれ $\frac{4}{18}$
これが冒頭に書いた「確率予想」です。
期待値を計算するとおよそ$2.2$となり、若干増加率が上がり、やはり指数関数的に増加することになります。
実験します
これ以上は思考が進まないので実験して終わりにします。
pythonで$f$を$1,000$回繰り返して、値と剰余を取得します。
def cal(n):
s=divmod(n,6)[1]
if s==0:
m=divmod(2n,3)[0]
elif s==1:
m=divmod(4n-1,3)[0]
elif s==2:
m=divmod(8n-1,3)[0]
elif s==3:
m=divmod(16n-9,3)[0]
elif s==4:
m=divmod(2n+1,3)[0]
elif s==5:
m=divmod(4n-2,3)[0]
return int(m)
import math
import sympy
n=2 #初期値
for i in range(1,1000+1):
print(f'{math.log(n)}\t{divmod(n,6)[1]}')
n=cal(n)
結果
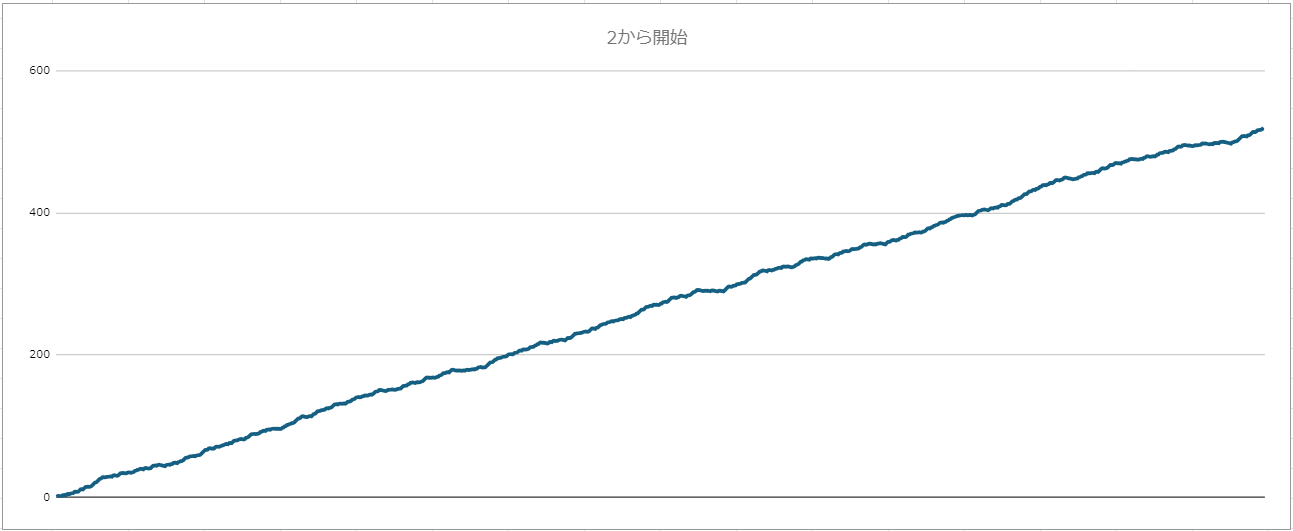
初期値2の場合
| mod 6 | 出現数 |
|---|---|
| 0 | 118 |
| 1 | 220 |
| 2 | 116 |
| 3 | 221 |
| 4 | 105 |
| 5 | 220 |
初期値29の場合

| mod 6 | 出現数 |
|---|---|
| 0 | 94 |
| 1 | 219 |
| 2 | 108 |
| 3 | 247 |
| 4 | 112 |
| 5 | 220 |
初期値7の場合

| mod 6 | 出現数 |
|---|---|
| 0 | 130 |
| 1 | 214 |
| 2 | 110 |
| 3 | 224 |
| 4 | 106 |
| 5 | 216 |
対数をとったグラフは線形に増加し、mod6の値の出現率もだいたい予想通りの結果になりました。
そもそもコラッツ予想が成り立っている初期値で実験しているので、当たり前と言えば当たり前です。
(しかしまあ、確率を仮定するのは直感としては本末転倒な気もします…)
あとがき
時間と知識があればもう少し考えられたかもしれませんが、ちょっと何と言うか…沼にはまっていく感じがするので笑、この辺りでお終いにしようと思います。
(誤りがあると思うのでご指摘いただけるとありがたいです)