結合法則を計算グラフで見てみよう

どうも

　こんにちは　ごてという者です
　Twitterで繋がりのあった みなと（@mntneko_）さんが4つ以上の群の元に対して結合法則を適用していいか真面目に証明してない人が多いのではないか、と言及していて　私は真面目に証明したことがなかったので考えた結果、楽しかったので記事にしようと思いました（記事化の許可を得ています！）

この記事の目標

　結合法則が$n$個の元に対しても使えることを示します！

前提知識

　群の言葉こそ使いますが高校数学を通っていれば読めると思います.

結合法則とは？

　群（というか半群）の定義に含まれる, 次の等式です.

　$(ab)c=a(bc)$.

　おおむね、どんな順番で計算してもいいという意味です

「二項」演算

　群には「二項」演算しか定められていません. 定義から$ab$は定義されているけど, $abc$は定義されていないということです. しかし, 結合法則があるので $abc$を$(ab)c$と解釈しても$a(bc)$と解釈しても問題がありません. なので我々は$abc$と書くことを許されています.

3つのときは大丈夫 では4つのときは？

　では, 4つの元の場合を考えてみましょう. たとえば次の式は、本当に成立するでしょうか？

　$((ab)c)d=a(b(cd))$.

　愚直に頑張ってみます.

　$((ab)c)d=(ab)(cd)=a(b(cd))$. できました.

　いや、これを見せられてもすぐにわからん！という意見もあると思うので丁寧に見ていきます.

　最初の変形は $(ab)$をひとかたまりと見ています. $ab=X$としてみます.

　$((ab)c)d=(Xc)d=X(cd)=(ab)(cd)$ というわけです.

　次の変形は $(cd)$をひとかたまりと見ています. $cd=Y$としてみます.

　$(ab)(cd)=(ab)Y=a(bY)=a(b(cd))$ ということですね！

　慣れてくれば記号に置かなくても見えてくると思います

問題を少し簡単にしてみる

　この記事の目標は, 結合法則を4つ以上の元に対しても使っていいのかという部分に答えることです. 無論使っていいのですが, ここからはそれを証明しようと思います. その前に, 問題を少し単純化します！
　それぞれ互いに等しいことを示すより, 全部同じ形に変形できることを示したほうがラクそうです. というわけで, 次の命題を考えます.

　これを証明できれば結合法則が成立していると言えます！

　$a_1(a_2(...(a_{n-1}{a}_n)...))$という表記がちゃんと書き表せているか不安なので意味が定まるように付け加えておくと,

$a,b,c,d,e$で考えたときの$a(b(c(de)))$,
$a,b,c,d,e,f,g,h,i$で考えたときの$a(b(c(d(e(f(g(hi)))))))$を考えています！

ここまでやってきましたが

　計算の過程を見やすくするために、計算グラフを導入します　ちゃんと定義はしませんが、感じ取ってください（え？）

計算グラフの例

　計算グラフは、演算の順序などをうまい具合にグラフ（ノードとかエッジとかの方）に表したものになります

手書き

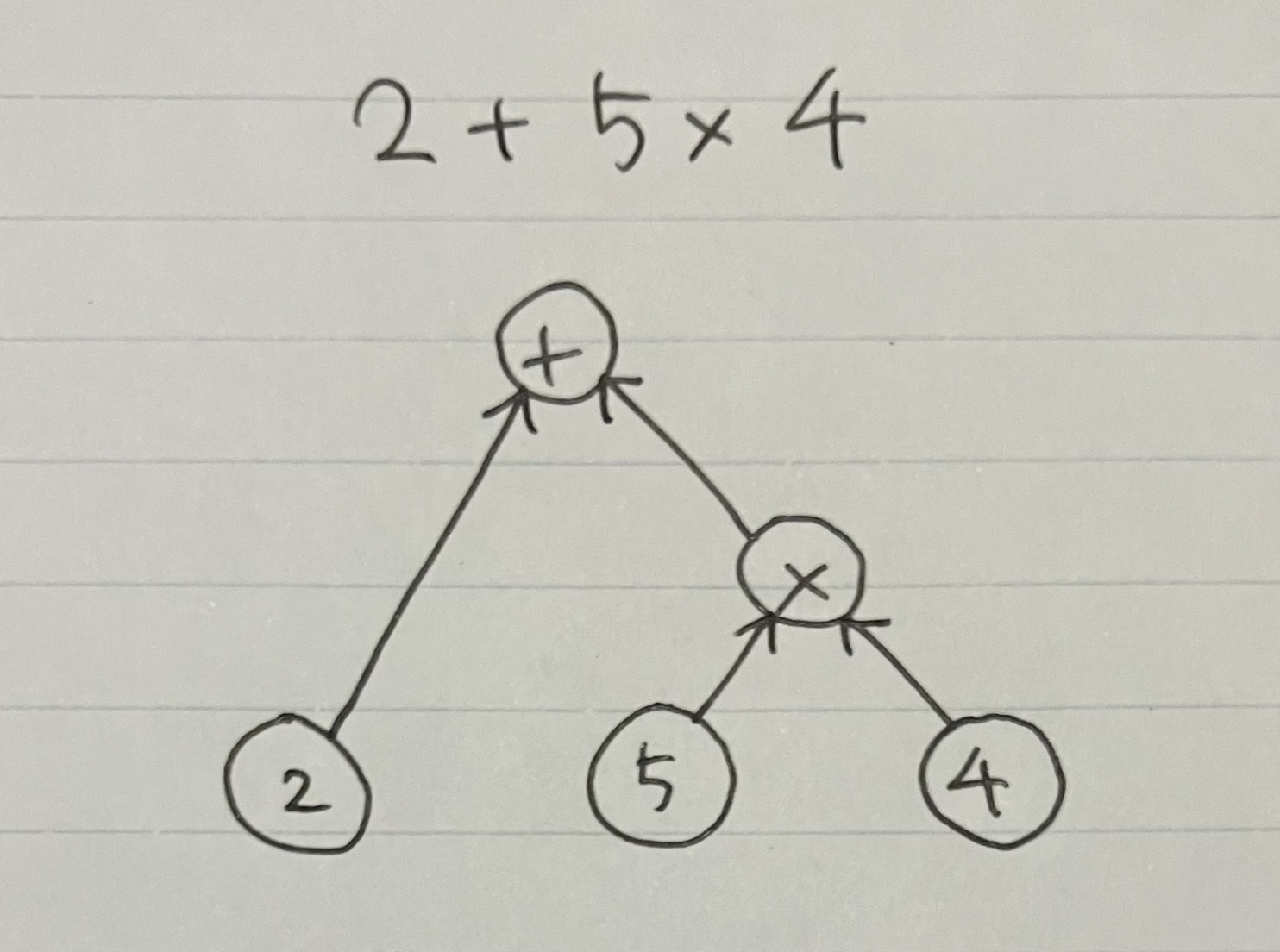
　上の画像は $2+5\times 4$ の式を表しています. $2,5,4$の数字の中で, $5$と$4$が先に結ばれていて, これは掛け算が先に計算されることを表せています.

もう1つ例

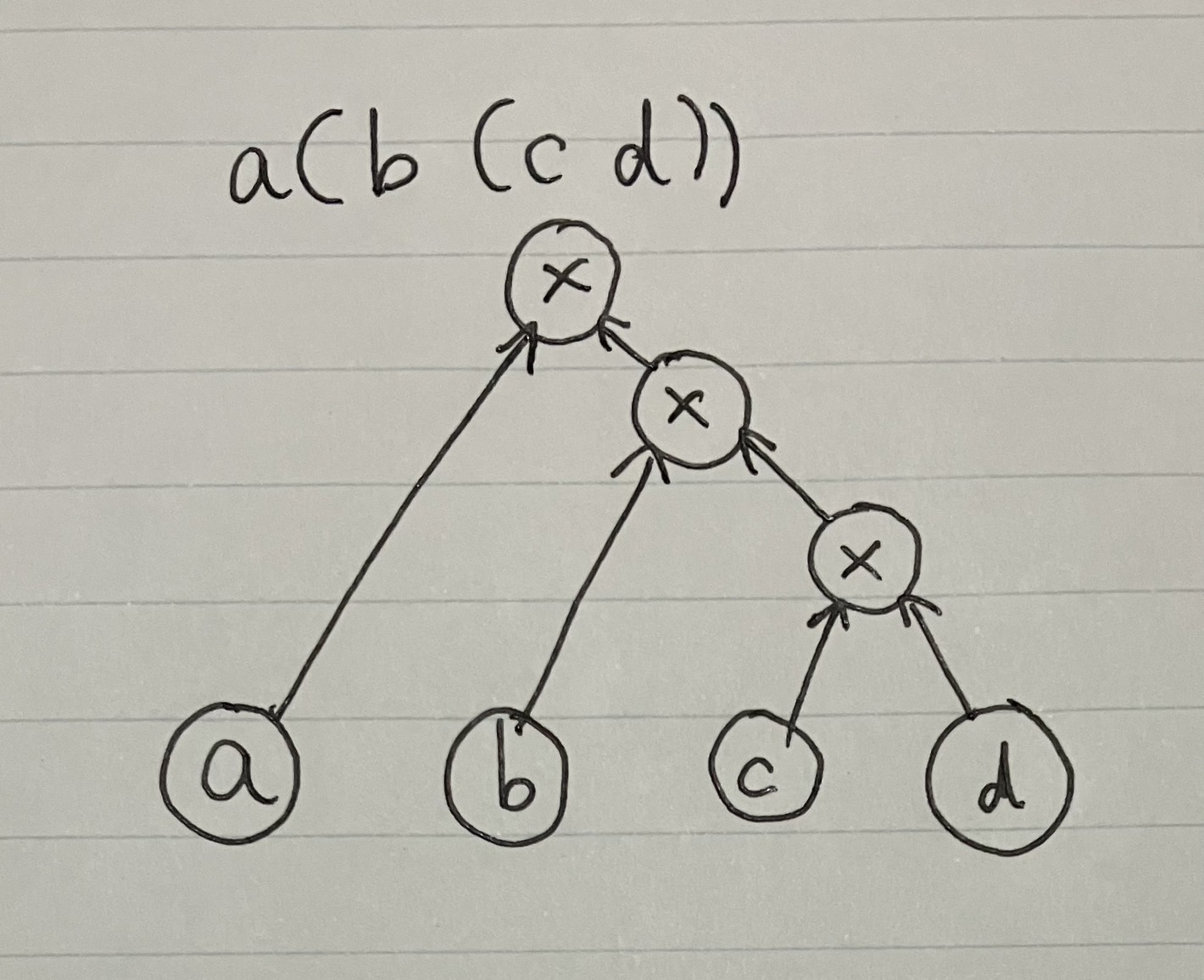
　これは$a(b(cd))$を表しています.

簡潔に書きます

　今回考える演算は一種類だけなので、演算子の部分を省略することにします　すると次のように簡潔に書くことができます.

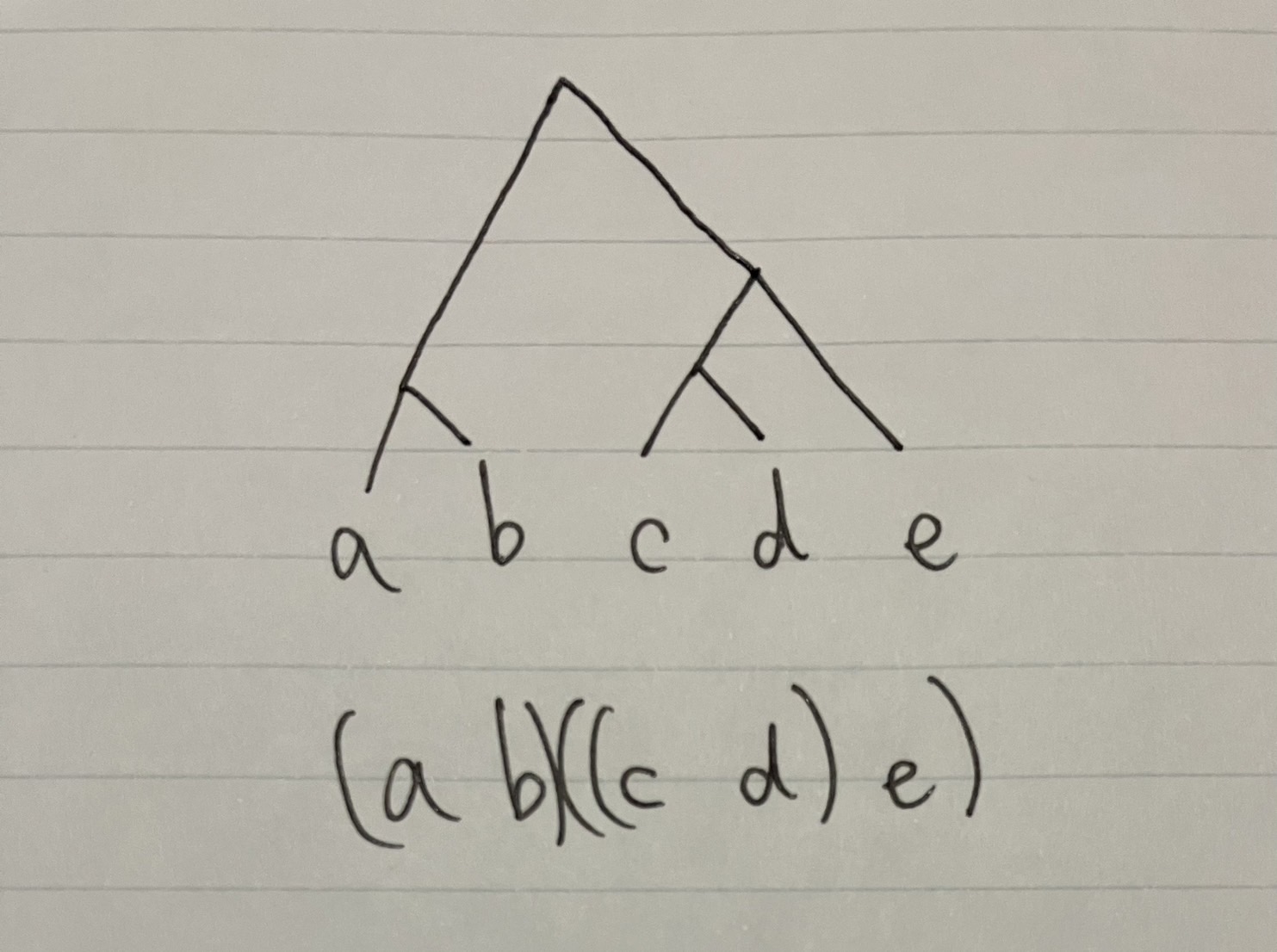
　すると結合法則は次のように表すことができます.

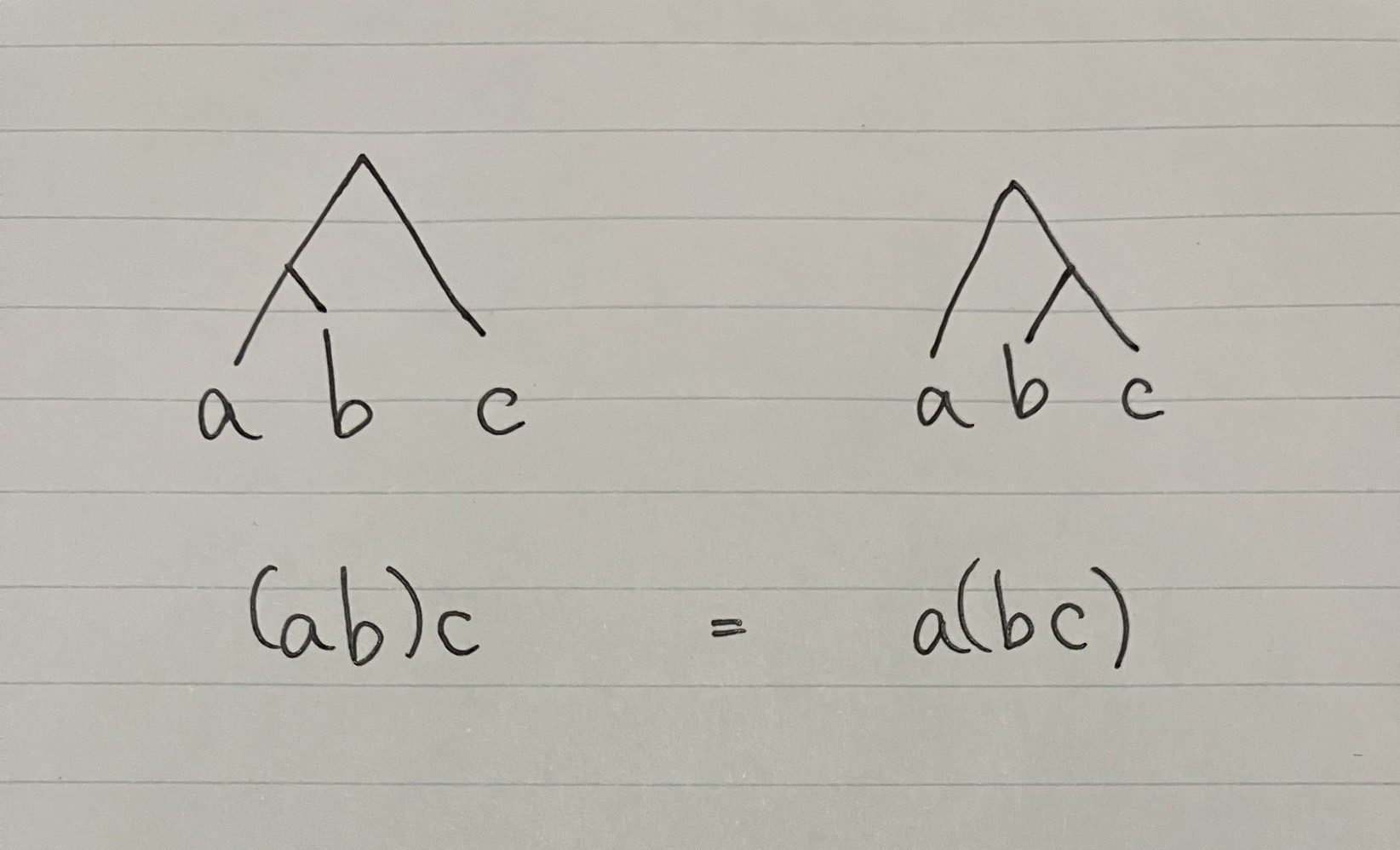　 結合法則

　この変形をもうちょっとわかりやすく捉えましょう. 一番近くの山を登って下るイメージです.
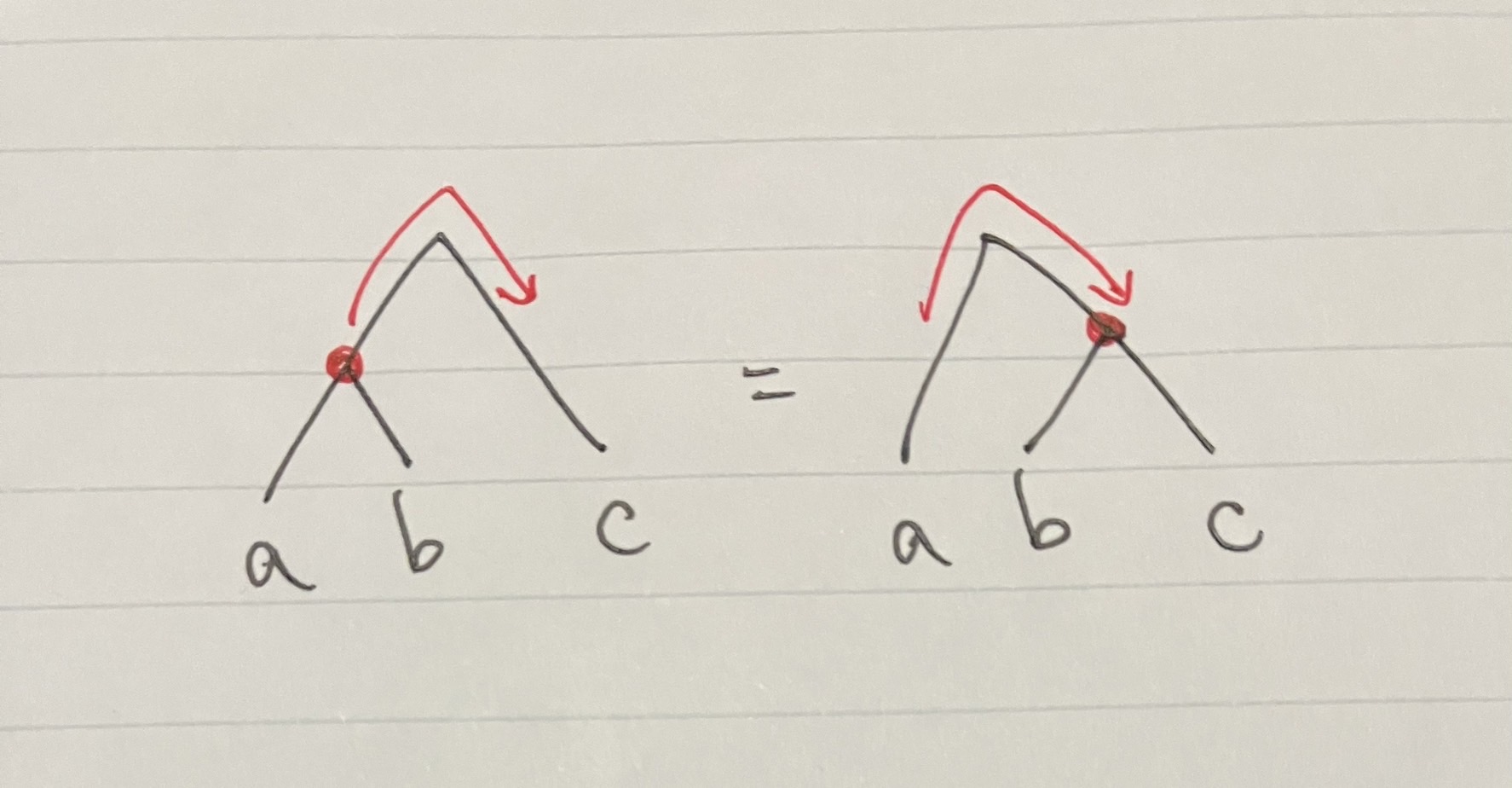　 ライデマイスター移動を思い出した

　実際に使うと次のような感じです.
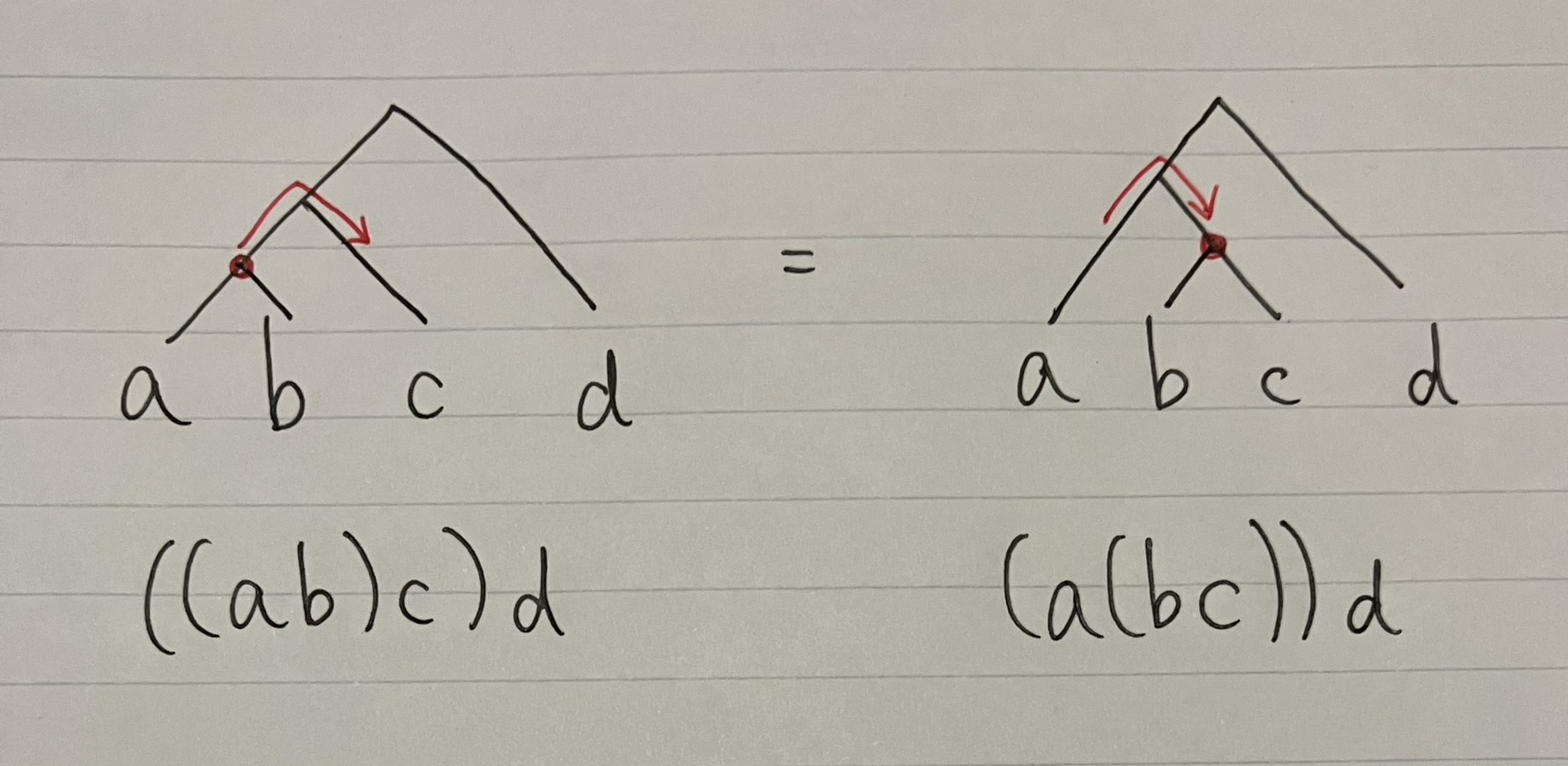　 適用例

　次の変形 $((ab)c)d=(ab)(cd)=a(b(cd))$ がどうなっているか脳内で補いながら見て考えてみてください.
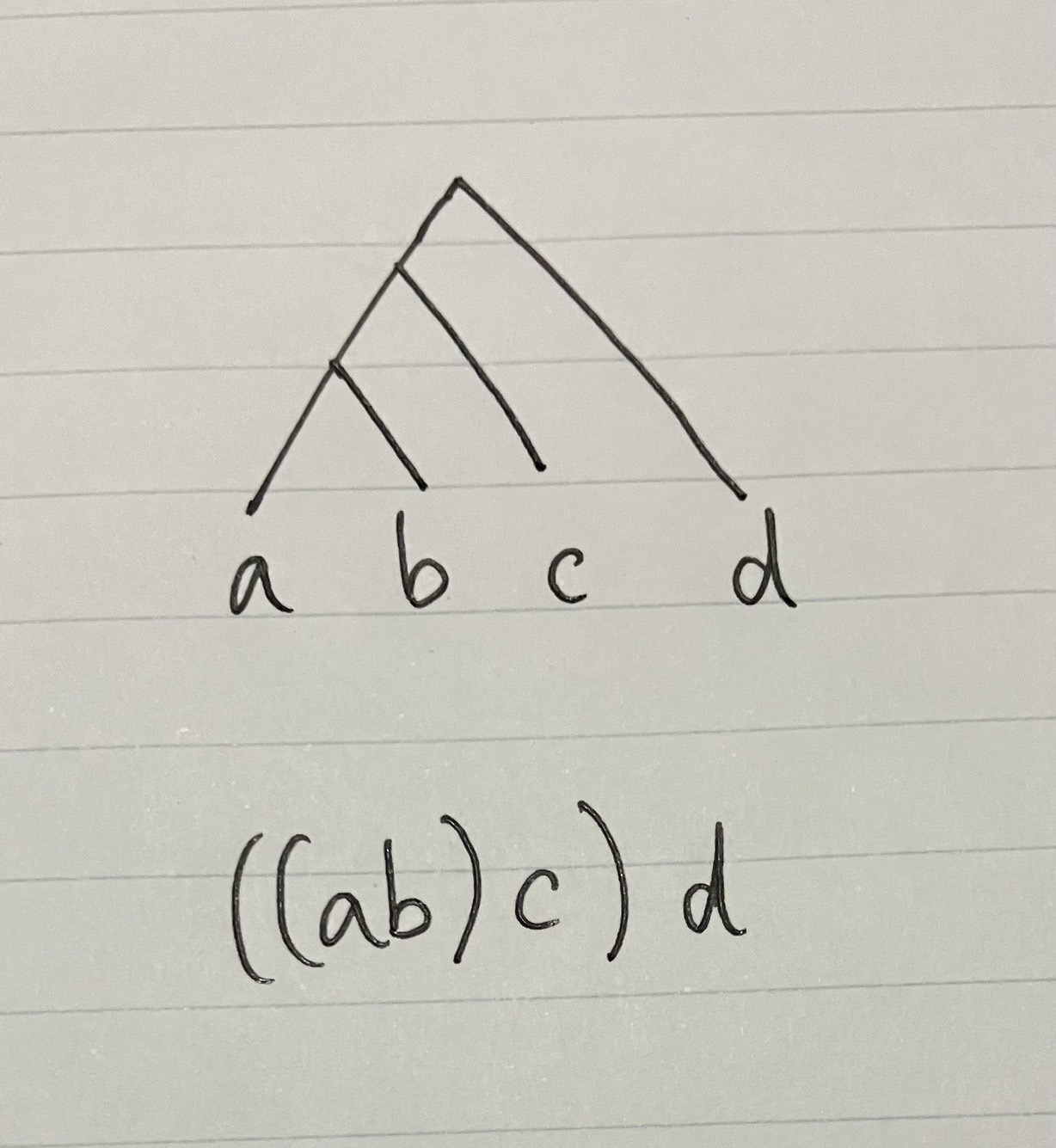　 abをひとかたまりと見て
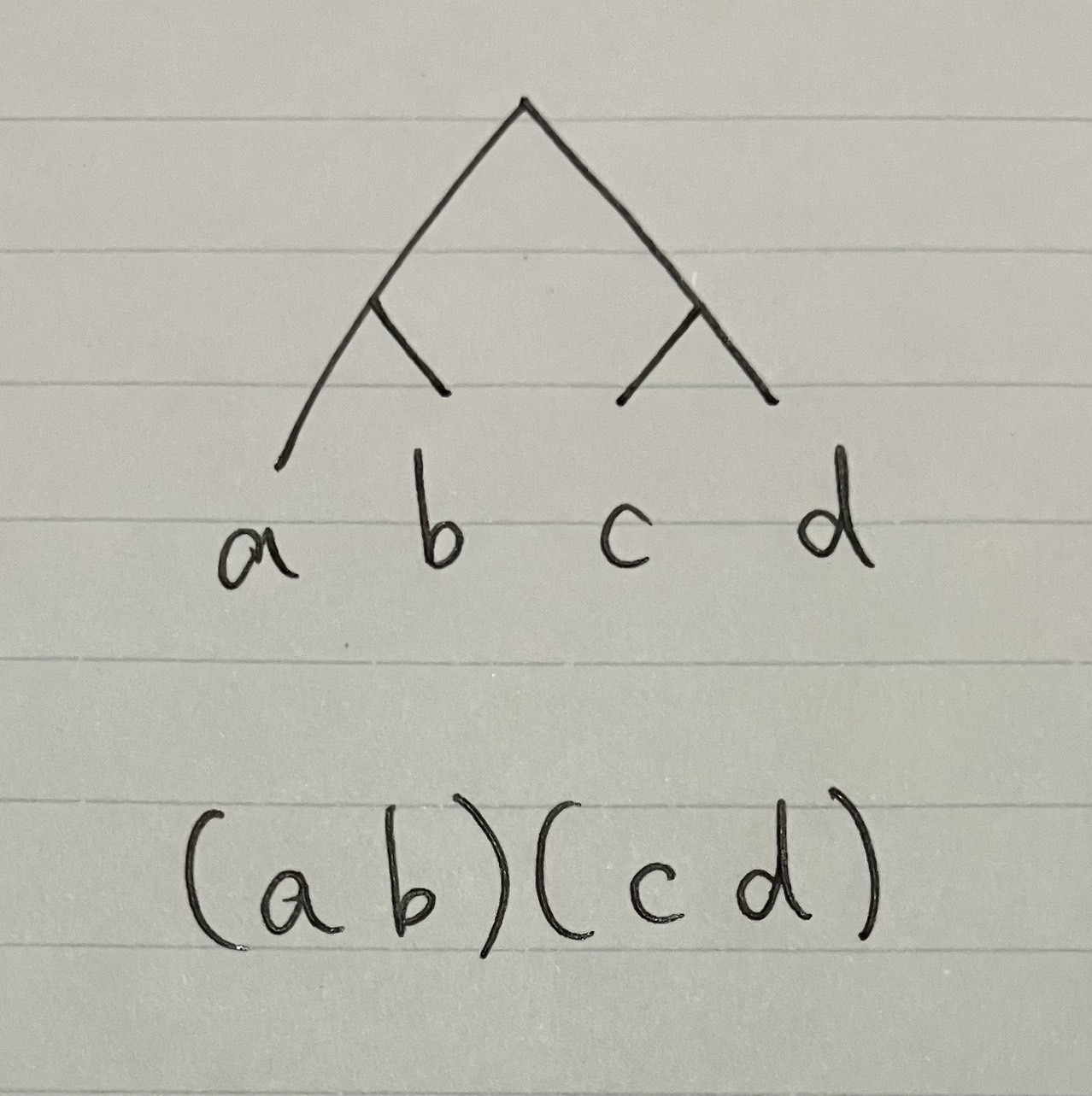　 cが山を越える
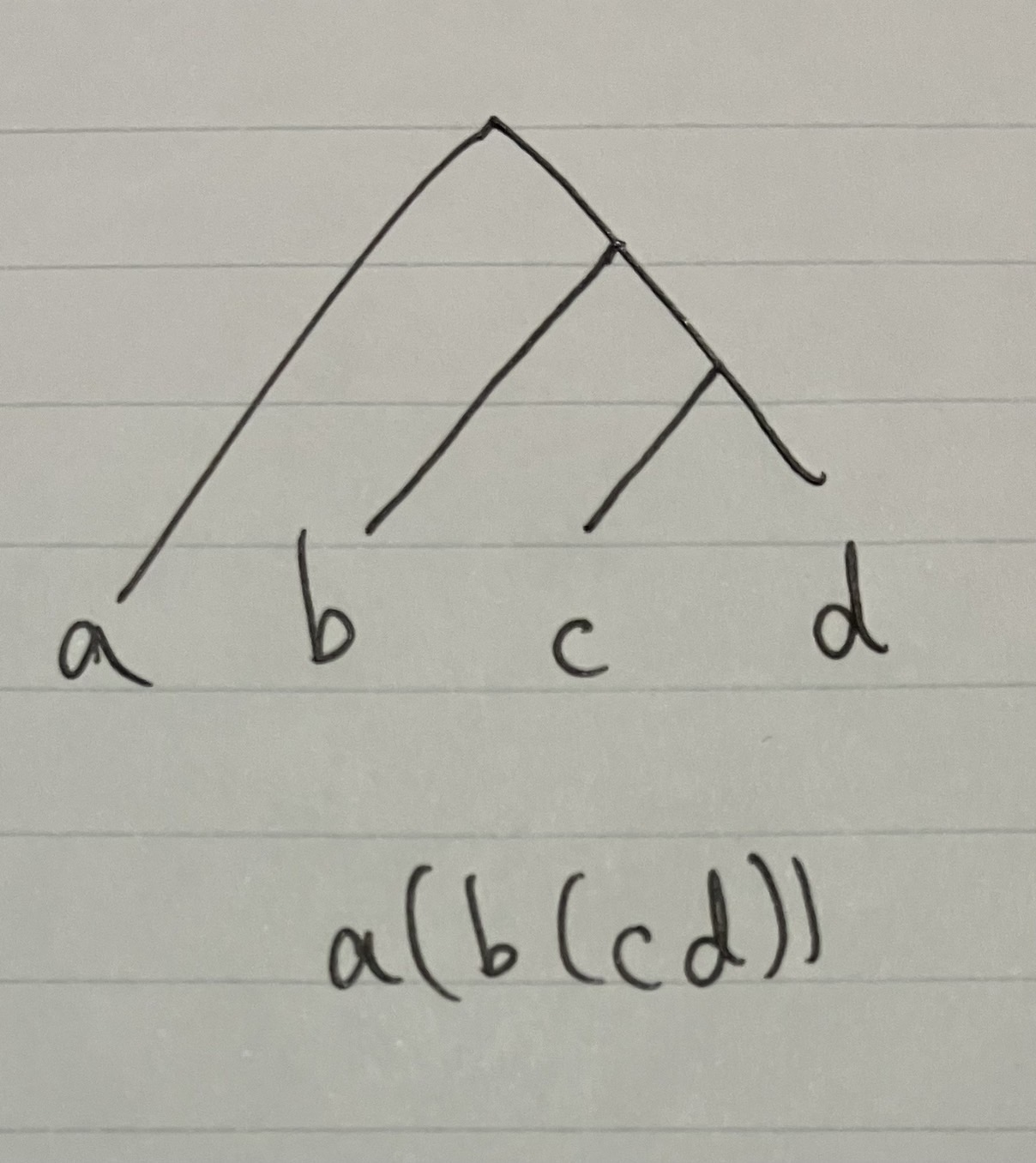　 bも山を越させる

何を示したかったか

　もう一度命題を見直してみます.

　最終的にすべて $a_1(a_2(...(a_{n-1}{a}_n)...))$ に変形したいという話でした.
　これを図にしてみます.

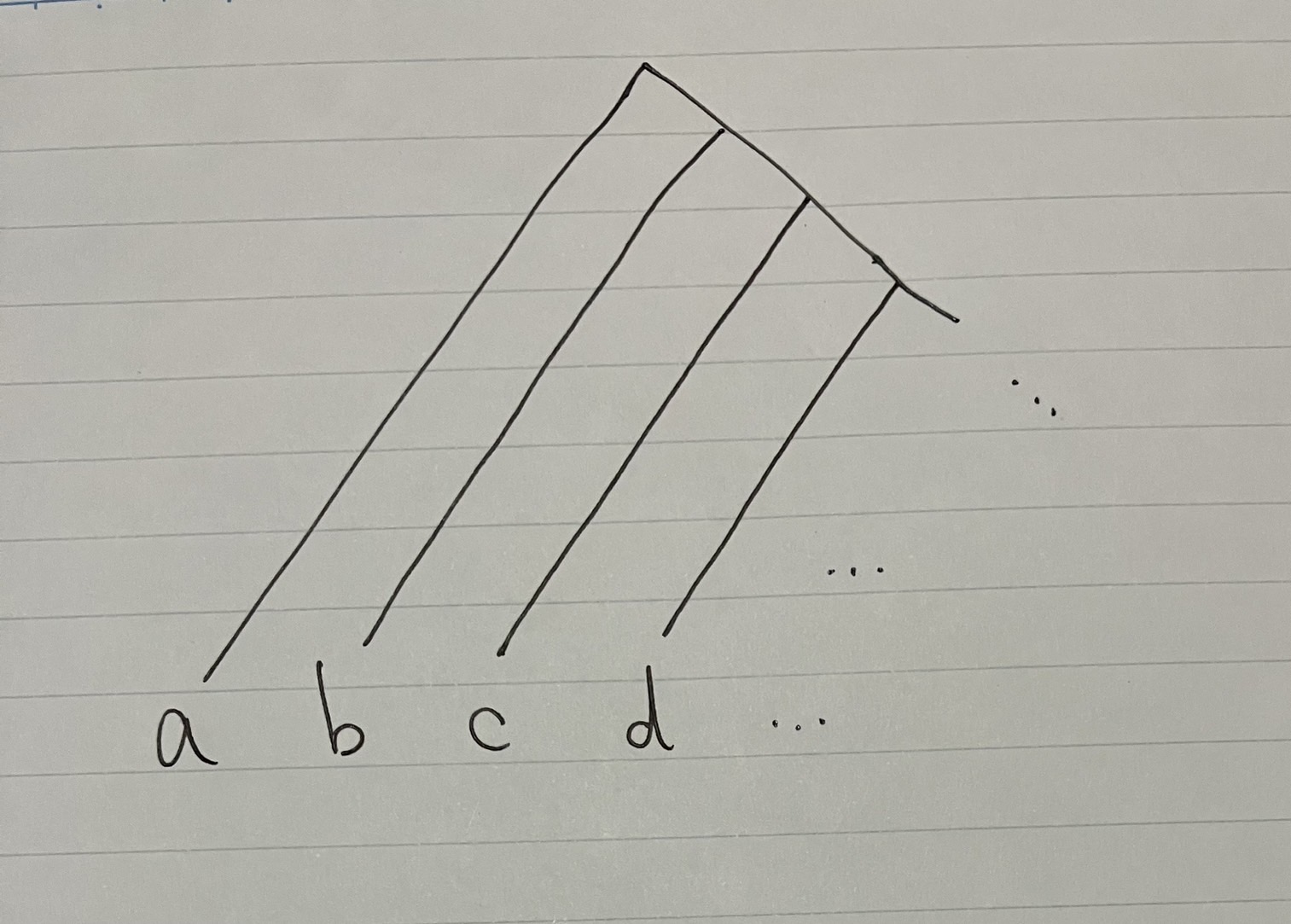こんな感じ

　つまり、すべての計算グラフをこういった形になるまで変形すればいいということです.
　$a,b,c,d,...$の順番でピーンと伸ばしていけばいい, と証明の手順を見通せるようになったと思います！

証明の流れ

　本当は帰納法を用いてしっかり証明を書きたいところですが、面倒なので簡単なイメージで済ましてしまいます.

　次の図を $a,b,c,d,...$ の積を計算グラフで表すと次のように表されるとします.

　 $a,b,c,d,...$の順番以外確定していない状況

　もし$ab$が繋がっていれば, その結合している点に一番近い山を越させます.
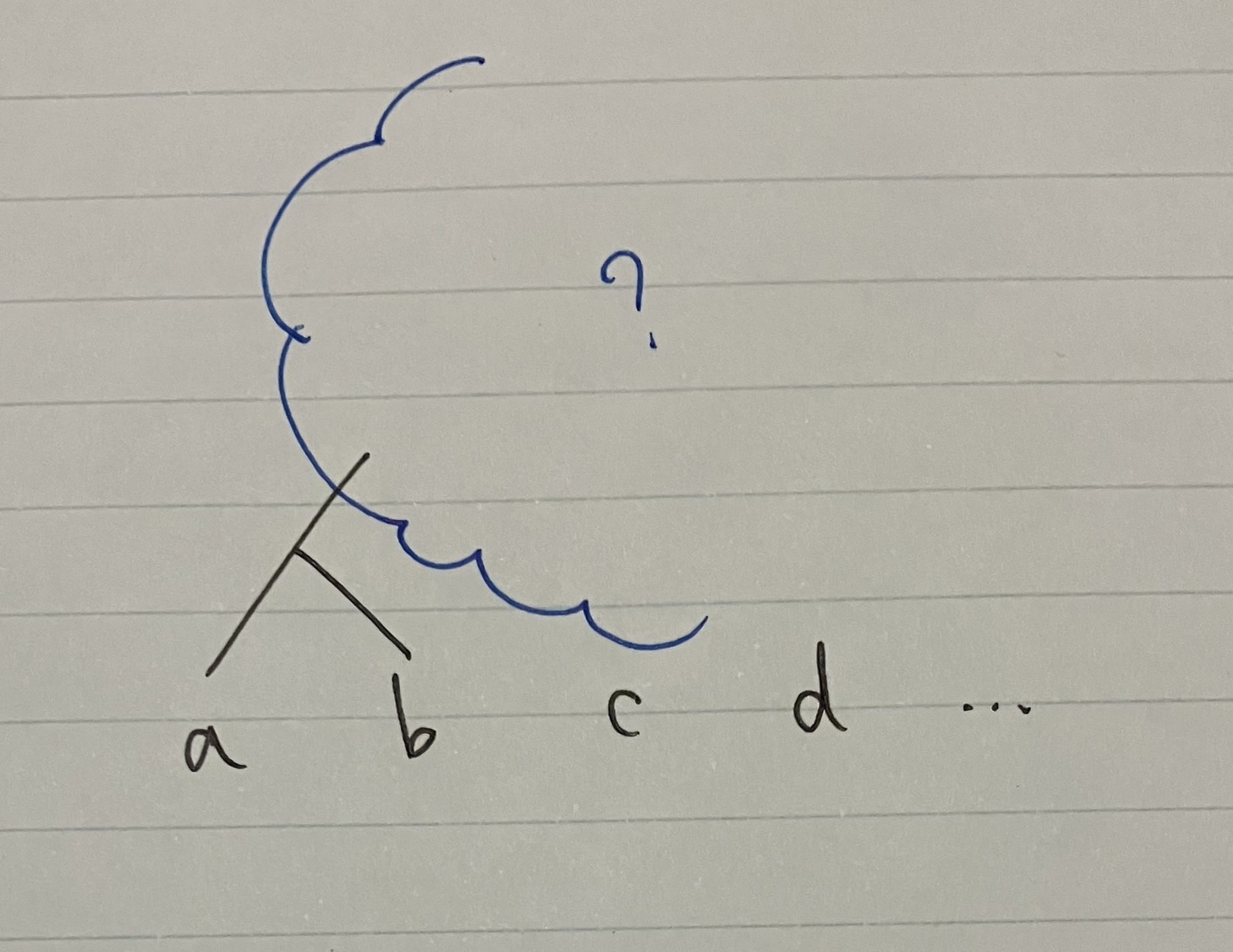　 もしこうなっているなら
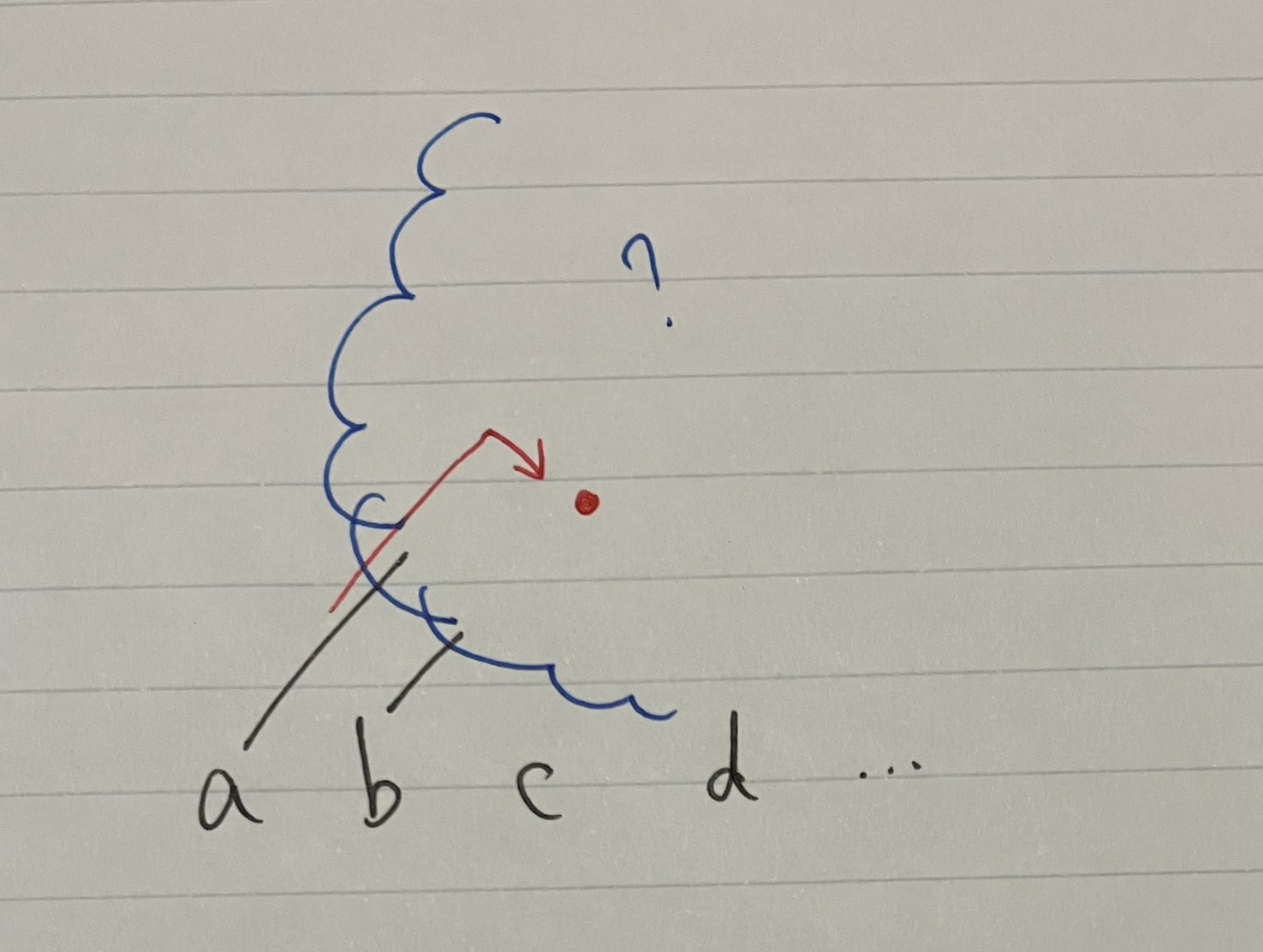　 こうする

　これを繰り返して, $a$と繋がっているものを山を越えるように動かしていきます.
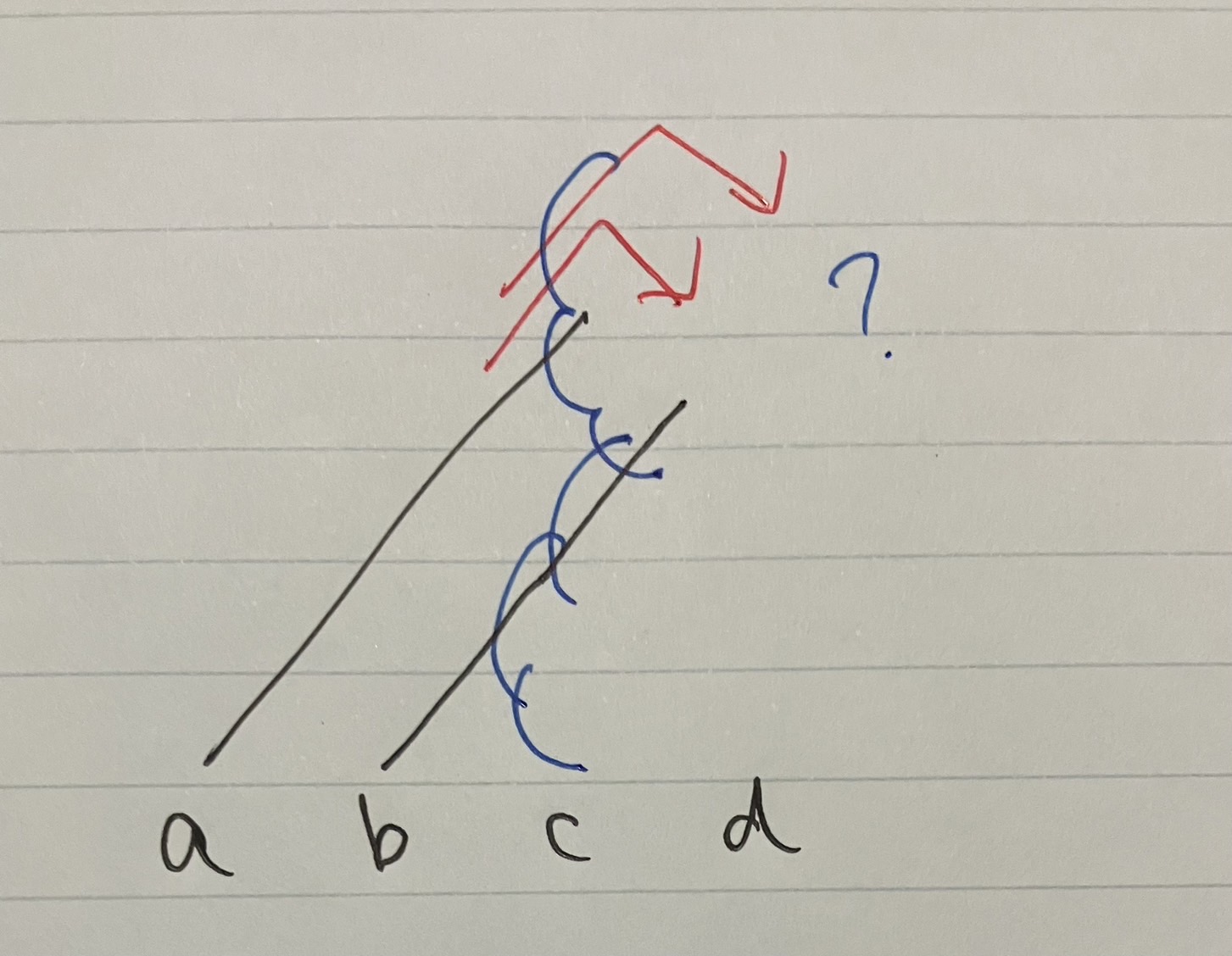　 一番上の山にたどり着くまで繰り返す

　これを最後まで行うと、次のようになるまで変形できるはずです！
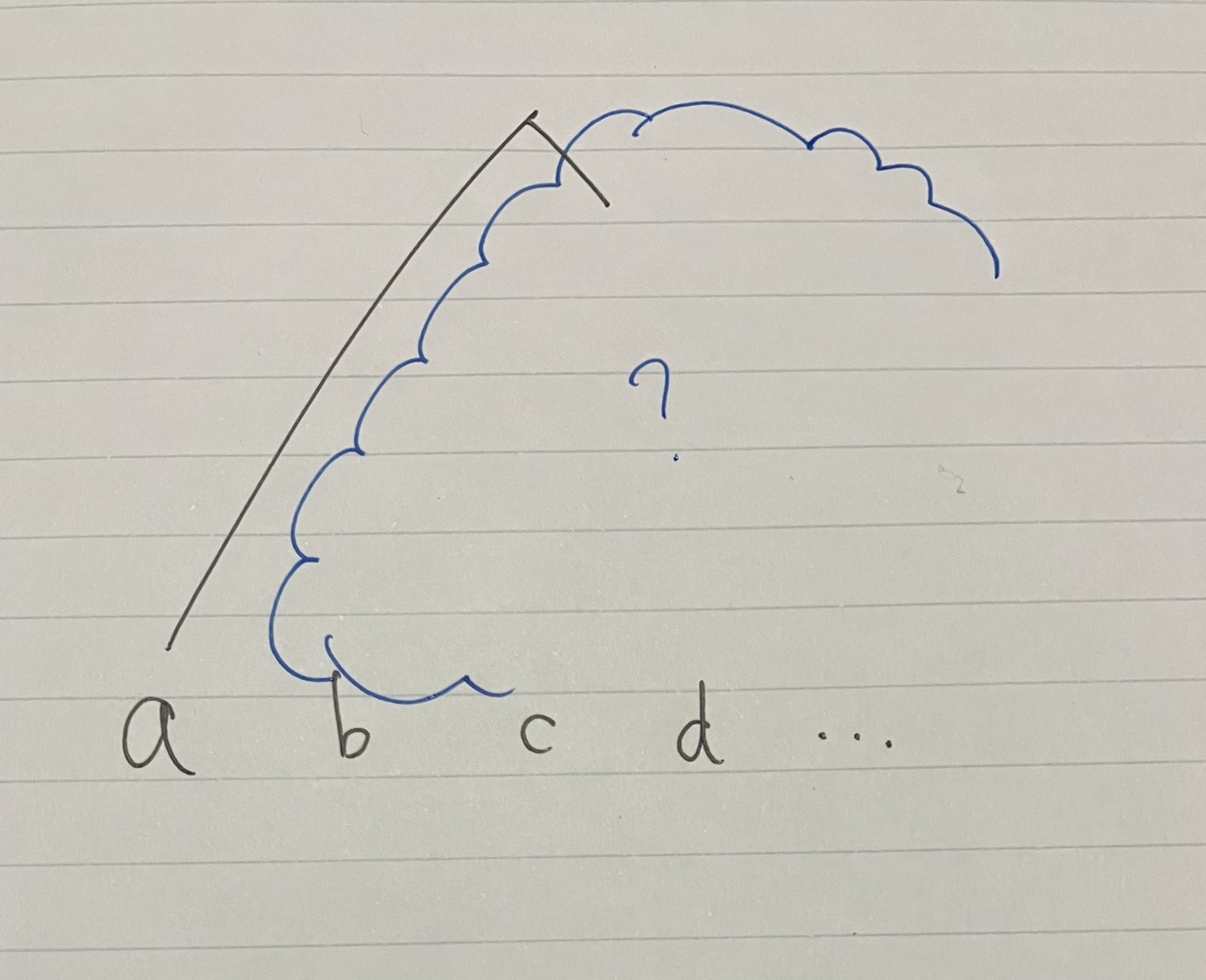　 こうできるはず

　そしてこれを, 次は$b$にその次は$c$に...... と繰り返していけば目的の形に変形できるはずです！これで証明完了！！！

まとめ

　疲れました！！！　ここまで読んでいただきありがとうございました～～～
　計算グラフといえば逆ポーランド記法とか誤差逆伝播法だと思いますが（数学科が馴染み深いわけではなさそう）、こういう見方もできるな～と思い記事にしました.
　見やすいだけでやっていることはちびちびかっこの位置を結合法則で動かしているだけなので, もし興味が出た場合はかっこをかっこのまま扱う証明も書いてみると面白いと思います.（帰納法で書きやすいのはこっちかもしれないです）

スペシャルサンクス

　記事化の許可をしていただきました みなと（@mntneko_）さん、ありがとうございました！！！