3200記念問題

はじめに

　この記事は私のX(旧Twitter)のフォロワー数が $3200$ 人を突破したことを記念して作った問題の解説記事です。

フォロワー3200人突破記念問題!
数学の問題です。画像の問題を解いてね!
難易度は
(1)EASY
(2)HARD pic.twitter.com/VrUWf5ca6Y

— ａｐｕ (@apu_yokai) December 24, 2023

　まず問題を紹介し、それから解答を解説します。

フォロワー $3200$ 人突破記念問題

　次のように、正方形のタイルを規則的に並べていくことを考えます。
　つまり、自然数 $n$ に対し、一辺の長さが $2n-1$ の正方形の内部に、一片の長さが $4$ つずつ少ない正方形を並べます。
　このとき、必要なタイルの枚数を $a(n)$ で表すことにします。

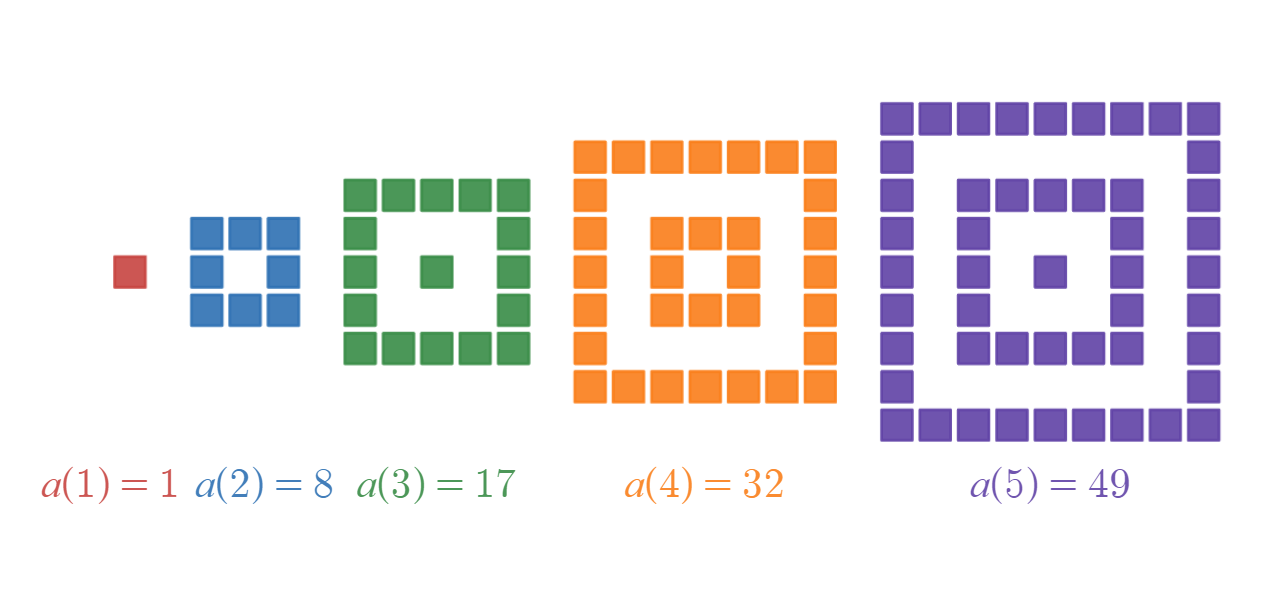正方形のタイルを規則的に並べる

　このとき、以下の $(1),(2)$ を解いてください。

$(1)$　$a(40)$ を求めてください。

$(2)$　${\displaystyle \sum_{n=1}^{\infty}\frac{1}{a(n)}}$　を求めてください。

解答編

(1) の解答

$(1)$　$a(40)$ を求めてください。

解法1

3200個の正方形

　実際に並べると図 $2$ のようになります。頑張って数えれば $3200$ 個であることがわかります。
　……冗談です。
　各正方形に使われるタイルの数が等差数列になっていることから、等差数列の和の公式で求めるのが一番簡単だと思います。

　${\displaystyle \begin{align} a(40)&=8+24+40+\cdots+312\\ &=\frac{20(8+312)}{2}\\ &=3200 \end{align} }$

(2) の解答

$(2)$　${\displaystyle \sum_{n=1}^{\infty}\frac{1}{a(n)}}$　を求めてください。

　まず、$a(n)$ を $n$ の式で表します。
　偶数のときと奇数のときで場合分けします。

【$n$ が偶数のとき】

　　${\displaystyle \begin{align} a(n)&=8+24+40+\cdots+(8n-8)\\ &=\frac{\frac{n}{2}(8+(8n-8))}{2}\\ &=2n^2 \end{align} }$

【$n$ が奇数のとき】
　一辺が $1$ の正方形だけは等差数列を構成しないので例外処理が必要です。

　　${\displaystyle \begin{align} a(n)&=1+\left(0+16+32+\cdots+(8n-8)\right)\\ &=1+\frac{\frac{n+1}{2}(0+(8n-8))}{2}\\ &=2n^2-1 \end{align} }$

まとめるとこうなります。

　まず、$\sum_{n=1}^{\infty}\frac{1}{a(n)}$が収束することを確認しましょう。

　$n\ge1$ のとき $a(n)\ge n^2$　ですから

　　${\displaystyle \begin{align} \sum_{n=1}^{\infty}\frac{1}{a(n)} &\le \sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}\\ \end{align} }$

　となります。
　すなわち、この級数は上に有界で単調増加しますので、収束します。各項は正ですから、絶対収束します。
　絶対収束する級数は和の順番を変えても同じ値に収束しますので、級数を「偶数項の和」と「奇数項の和」に分けます。

「偶数項の和」はゼータ関数の特殊値に帰結して

　${\displaystyle \begin{align} \sum_{n=1}^{\infty}\frac{1}{2(2n)^2} &=\frac{\zeta(2)}{8}\\ &=\frac{\pi^2}{48}\\ \end{align} }$

「奇数項の和」はちょっと面倒ですが以下のように計算できます。

まず次の補題を示します。

　補題 $1$ に $z=\pi x$ を代入して両辺に $2\pi^2 x$ を乗じます。
　${\displaystyle \sum_{n=1}^{\infty} \frac{2x}{n^2-x^2} =\frac{1}{x}-\pi\cot{\pi x} }$

　補題 $2$ に $x=\frac{1}{\sqrt2}$ を代入してから、次のように変形していきます。

　${\displaystyle \sum_{n=1}^{\infty} \frac{\sqrt{2}}{n^2-\frac{1}{2}} =\sqrt{2}-\pi\cot{\frac{\pi}{\sqrt{2}}} }$

　${\displaystyle \sum_{n=1}^{\infty} \frac{2\sqrt{2}}{2n^2-1} =\sqrt{2}-\pi\cot{\frac{\pi}{\sqrt{2}}} }$

　${\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n^2-1} =\frac{1}{2}-\frac{\pi}{2\sqrt{2}}\cot{\frac{\pi}{\sqrt{2}}} }$

　補題 $2$ に $x=\frac{1}{2\sqrt2}$ を代入してから、次のように変形していきます。

　${\displaystyle \sum_{n=1}^{\infty} \frac{\frac{1}{\sqrt{2}}}{n^2-\frac{1}{8}} =2\sqrt{2}-\pi\cot{\frac{\pi}{2\sqrt{2}}} }$

　${\displaystyle \sum_{n=1}^{\infty} \frac{4\sqrt{2}}{8n^2-1} =2\sqrt{2}-\pi\cot{\frac{\pi}{2\sqrt{2}}} }$

　${\displaystyle \sum_{n=1}^{\infty} \frac{4\sqrt{2}}{2(2n)^2-1} =2\sqrt{2}-\pi\cot{\frac{\pi}{2\sqrt{2}}} }$

　${\displaystyle \sum_{n=1}^{\infty} \frac{1}{2(2n)^2-1} =\frac{1}{2}-\frac{\pi}{4\sqrt{2}}\cot{\frac{\pi}{2\sqrt{2}}} }$

　補題 $3$ の両辺から補題 $4$ の両辺を引くと次のようになります。

　左辺に注目します。左辺第 $2$ 項は左辺第 $1$ 項の偶数項の和ですから、引き算の残りは奇数項の和となります。つまり

　${\displaystyle \sum_{n=1}^{\infty}\frac{1}{2n^2-1} -\sum_{n=1}^{\infty} \frac{1}{2(2n)^2-1}= \sum_{n=1}^{\infty}\frac{1}{2(2n-1)^2-1} }$

　後は、右辺を整理していきます。

　${\displaystyle \begin{align} \sum_{n=1}^{\infty} \frac{1}{2(2n-1)^2-1} &=\frac{\pi}{4\sqrt{2}}\cot{\frac{\pi}{2\sqrt{2}}}-\frac{\pi}{2\sqrt{2}}\cot{\frac{\pi}{\sqrt{2}}}\\ &=\frac{\pi}{4\sqrt{2}}\cot{\frac{\pi}{ 2\sqrt{2}}}-\frac{\pi}{2\sqrt{2}}\cdot\frac{1}{2}\left(\cot{\frac{\pi}{2\sqrt{2}}}-\tan{\frac{\pi}{2\sqrt{2}}}\right)\\ &=\frac{\pi}{4\sqrt{2}}\tan{\frac{\pi}{2\sqrt{2}}}\\ \end{align} }$

$2$ 行目の変形に $\cot$ の倍角公式
　${\displaystyle \cot(2x)= \frac{1}{2}\left(\cot(x)-\tan(x)\right) }$

を使いました。

　これで問題の級数の和を求める準備ができました!

　${\displaystyle \begin{align} \sum_{n=1}^{\infty}\frac{1}{a(n)} &=\sum_{n=1}^{\infty}\frac{1}{2(2n)^2}+ \sum_{n=1}^{\infty}\frac{1}{2(2n-1)^2-1}\\ &=\frac{\pi^2}{48}+\frac{\pi}{4\sqrt{2}}\tan{\frac{\pi}{2\sqrt{2}}} \end{align} }$

おわりに

　あらためて、$a(n)$ の成長の様子を観察してみましょう。

画像の名前

　まるで花火のようにも見えておめでたいですね。
　これからもどんどんフォロワーさんの輪がこんな風に広がっていったらいいな、と思います。
　今後ともよろしくお願いします!