近接固有値に属する固有ベクトルの計算困難性について

近接固有値に属する固有ベクトルの計算困難性

非常に近い値をもつ固有値を近接固有値という．一般に，近接固有値に属する固有ベクトルを数値計算することは困難な課題である．
まずは具体的な例でこれを確認してみよう．

行列の近接固有値

実数$t \in\mathbb{R}$ に対して実対称行列 $A(t)$ を
\begin{equation} A(t) = \begin{pmatrix} 1 & t \\ t & 1 \end{pmatrix} \end{equation}
と定める．解析的に計算される$A$ の固有値は
\begin{equation} \lambda_1(t) = 1-|t|,~~\lambda_2(t) =1+|t| \end{equation}
となる．$t\approx 0$ のときに $ \lambda_1(t)\approx \lambda_2(t)$となるので，この２つの固有値は近接固有値と呼ばれる．
ここで，
\begin{equation} \mathbf{u}_1 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1 \end{pmatrix}\quad \mathbf{u}_2 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1 \end{pmatrix} \end{equation}
は解析的に計算される$A$ の固有ベクトルとなる．
ただし，$t$ の符号によって固有値・固有ベクトルの対応関係が変化することに注意する必要がある．
実際は，
$ t>0$ のときは$(\lambda_1, \mathbf{u}_1)$, $(\lambda_2, \mathbf{u}_2)$ が行列$A$の固有対となり，
$ t< 0$ のときは$(\lambda_1, \mathbf{u}_2)$, $(\lambda_2, \mathbf{u}_1)$ が行列$A$の固有対となる．
$t=0$のときは固有値は重複$(\lambda_1=\lambda_2)$となり，$\mathbf{u}_1,\mathbf{u}_2$ が固有空間の基底となる．

図1に$t=0$ の近傍において，固有値$\lambda_1(t),\lambda_2(t)$の$t$に関するグラフを示した．

$\lambda_k(t)~(k=1,2)$のグラフ

近接固有値に属する固有ベクトルの数値計算

近接固有値に属する固有ベクトルを計算することが難しいことを感覚的に理解するために，
固有値が近接する場合($t\approx 0$)における行列$A(t)$の固有ベクトルをべき乗法を使って計算機で求めてみよう．

べき乗法とは，行列 $A$ の最大固有値に対応する固有ベクトルを反復計算により近似的に求める手法である．
初期ベクトル $v^{(0)}$ を適当に選び，以下の反復を行う：
\begin{equation} v^{(k+1)} = \frac{A\, v^{(k)}}{\|A\, v^{(k)}\|}\,, \end{equation}
ここで $\|\cdot\|$ はユークリッドノルムを表す．
理論的には十分な反復回数により$v^{(k)}$ は $A$ の最大固有値に対応する固有ベクトルに収束することが知られているが，
固有値間の差が非常に小さい場合には丸め誤差の影響が顕著となり，計算結果が真の解から回転してしまう問題が生じる．
以下に，実際の数値計算環境下での検証例について述べる．
ここでは，$t>0$の場合に行列
\begin{equation} A(t) = \begin{pmatrix} 1 & t \\ t & 1 \end{pmatrix} \end{equation}
を考える．解析的に求めた固有値は
\begin{equation} \lambda_1 = 1 - t,\quad \lambda_2 = 1 + t \end{equation}
であり，最大固有値 $\lambda_2$ に対応する真の固有ベクトルは
\begin{equation} \mathbf{v}_{\mathrm{true}} = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1 \end{pmatrix}\, \end{equation}
となる．
数値実験では，MATLAB の double 精度環境下においてべき乗法による反復計算を用い，
最大反復回数を $1000$ 回，収束判定の閾値を $10^{-12}$ と設定した．
また，入力パラメータ $t$ は $10^{-5}$ から $10^{-1}$ まで対数スケールで変化させ，各 $t$ に対して
べき乗法により計算された固有ベクトル $\mathbf{v}$ と真の固有ベクトル $\mathbf{v}_{\mathrm{true}}$との間の回転角
\begin{equation} \theta = \arccos\Bigl(|\mathbf{v}_{\mathrm{true}}^T \mathbf{v}|\Bigr) \end{equation}
を求めた．図2は横軸を $t$（対数スケール），縦軸を回転角 $\theta$（度）として，
べき乗法により求めた近似固有ベクトルと解析的に求めた真の固有ベクトルとの間の回転角の変化を示すものである．
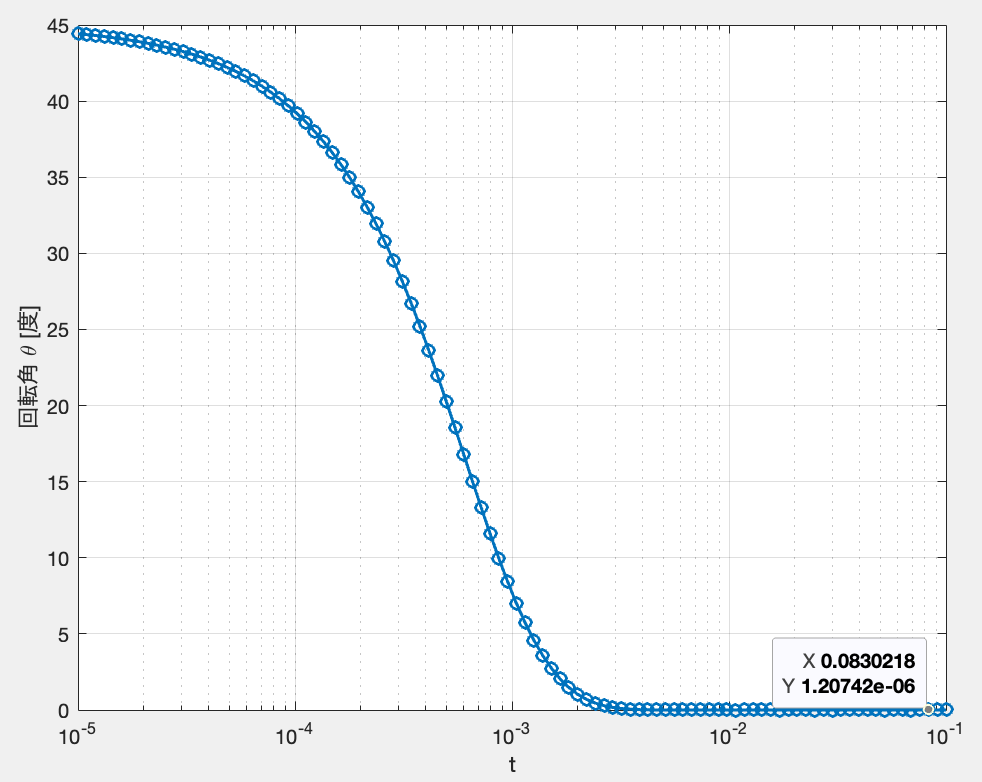近似固有ベクトルの回転角

$t$が$0$に近づくに従って回転角が大きくなっていることを見ると，この方法では$t$が小さいときに正しい近似固有ベクトルを計算できていないことが分かる．

手法や設定により異なるものの，丸め誤差がある限り普通の数値計算では固有ベクトルを正しく計算できる$t$の下限が存在する．この意味で，数値計算を用いて「すべての$t\in(0,t_0)$ に対して$ \mathbf{\hat{v}}\approx\mathbf{v}_{\mathrm{true}}$となる」近似固有ベクトル$\mathbf{\hat{v}} $を求めることはill-posed problem である．

ディリクレラプラシアンの近接固有値

角度$\theta\in (0,\pi/3)$に対して，次の頂点を持つ三角形$T^\theta$を考えよう：
\begin{equation} (0, 0),~(1, 0),~(\cos\theta, \sin\theta). \end{equation}

三角形領域$T^\theta$において，ラプラシアンのディリクレ固有値問題は次のように定式化される：
\begin{equation} -\Delta u = \lambda u \quad \text{in } T^\theta, \quad u = 0 \quad \text{on } \partial T^\theta, \tag{1} \end{equation}
ここで関数 $u$ は固有関数と呼ばれ，$\lambda$ は固有値と呼ばれる．
ただし，2次元領域におけるラプラシアン$\Delta$は次式で定義される微分作用素である：
\begin{equation} \Delta := \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}. \end{equation}
スペクトル定理によりラプラシアンの固有値は可算無限個存在し，非減少の実数列をなす．
三角形領域$T^\theta $は連結であるから第一固有値$\lambda_1$は単純あり，固有値の列を次のように表すことができる：
\begin{equation} 0 < \lambda_1 < \lambda_2 \leq \lambda_3 \leq \dots \to \infty. \end{equation}

固有値の近似計算

$\theta=\pi/3$のとき，三角形$T^\theta$は正三角形となる，
$T^\theta$が正三角形に近いときの固有値$\lambda_2,\lambda_3$の挙動に注目してみよう．
McCartin により，$\theta=\pi/3$のときこれらの固有値は重複($\lambda_2=\lambda_3 $)となることが知られている．
図３は$\theta\approx\pi/3$のとき，数値計算により$\theta$に関する$\lambda_2,\lambda_3 $のグラフを描いたものである．
$\theta=\pi/3$で重複固有値が存在し，その近傍で$\lambda_2,\lambda_3 $が近接固有値となっていることが分かる．

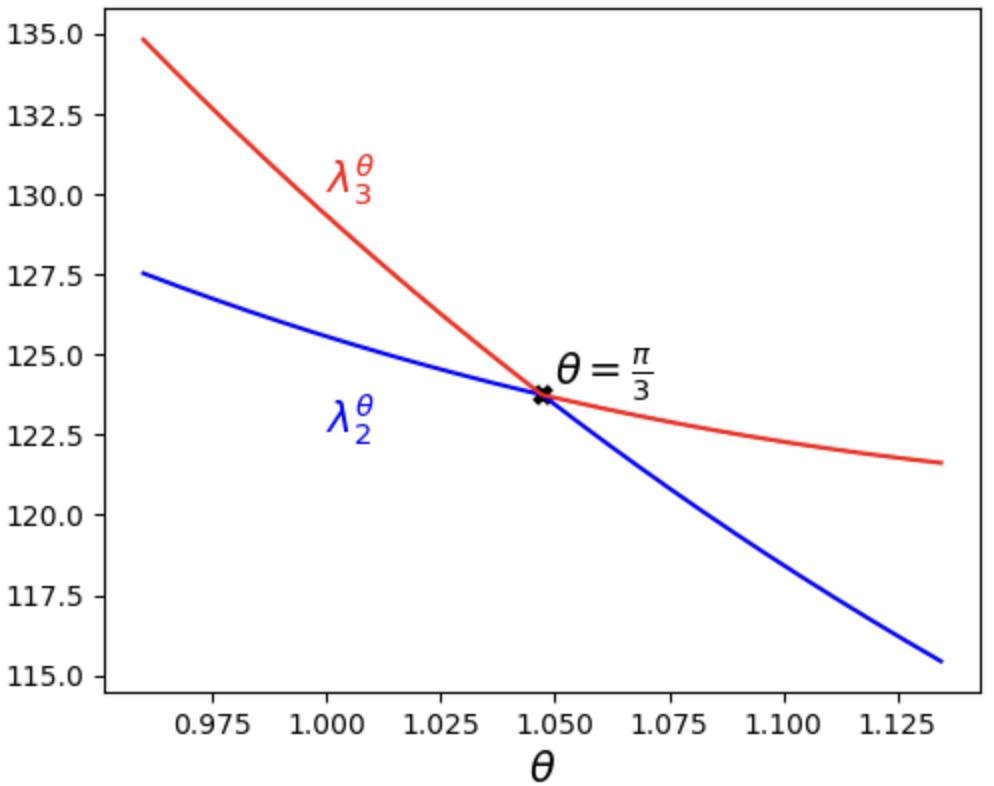第2,3固有値の挙動

固有値の差分商公式と近接固有値に属する固有関数の数値計算

偏微分方程式の数値解法の１つである有限要素法を用いると，ラプラシアンの固有値問題 (1) は離散化され，固有値・固有関数の数値計算を次のような形式の一般化固有値問題を解くことに帰着できる：
\begin{equation} Mx=\hat\lambda Nx~~\tag{2} \end{equation}
ただし，$M,N$は同じサイズを持つ正定値対称行列である．

正三角形に近い形状をもつ三角形領域$T^\theta~(\theta\approx \pi/3)$の場合のように，もとの固有値問題 (1) の固有値が近接する場合には，行列固有値問題 (2)を解くことによって得られる近似固有値$\hat\lambda$も近接し，本ノートの前半で説明したようなことと同様の現象が起こり，通常の方法ではうまく固有ベクトル$x$を計算することができない．(したがって，固有関数もうまく計算できない．)

ところが「固有値の差分商公式」を用いて計算結果を補正することにより，近接固有値に属する固有関数もうまく数値計算することができる(かもしれない)．

注意書き１：ここから先に書かれていることは別に論文で裏付けられたことではないので注意(ここから前もそうですが)

固有値の差分商公式と近似固有関数の補正

差分商公式の主張を説明する．

• パラメータ $p = (x, y) (\in \mathbb{R}^2)$ に対して，頂点が $(0, 0),(1, 0),(x, y)$ である三角形領域を $T^p$ とする．

• 固有値 $\lambda_{n}^p, \cdots, \lambda_{N}^p$ が $p$ において重複している，つまり
  $ \lambda_{n}^p = \cdots = \lambda_{N}^p (=: \lambda) $
  であると仮定する．
  ここで，$E$ を固有値 $\lambda$ に対応する固有空間とする．

• $t > 0,e \in \mathbb{R}^2$ かつ $\|e\|_2 = 1$ のとき，$p_t := p + te (=: (\tilde{x}, \tilde{y}))$ を $p$ の摂動とする．記号を簡略化するために，$T^t := T^{p_t}$，$T^0 := T^p$，および $\lambda_i^t := \lambda_i^{p_t}$ と表す．固有値 $\lambda_{n}^t, \cdots, \lambda_{N}^t$ に対応する線形独立な固有関数をそれぞれ $u_{n}^{t}, \cdots, u_{N}^{t}$ とする．

• また，$S_t: \mathbb{R}^2 \to \mathbb{R}^2$を三角形領域 $T^0$ を $T^t$ に写す線形変換とする．

• $\tilde{u}_i^t := u_i^t \circ S_t (\in H^1_0(T^0))$（$i = n, \cdots, N$）として，\begin{equation} \widetilde{E}_t := \text{span}\{\tilde{u}_n^t, \cdots, \tilde{u}_N^t\} \quad (\subset H_0^1(T^0)) \end{equation}
  と定める．

• さらに，固有値の差分商を
  $ D_t \lambda_i := (\lambda_i^t - \lambda)/t \quad (i = n, \cdots, N) $
  と表し，次のように $2 \times 2$ 行列 $P_t^e$を定義する：$ P_t^e := \left( S_t^{-1} S_t^{-\intercal} - I \right)/t.$

これらの設定のもと，以下の差分商公式が成り立つ：

注意書き２：ここから先に書かれていることは引用しているプレプリントの結果とは関係ありません

さて前節では，正三角形$T^p(p=(\cos(\pi/3),\sin(\pi/3))$では$\lambda_2,\lambda_3$が近接固有値となる事に触れた．
以下では，正三角形$T^p$$(p=(\cos(\pi/3),\sin(\pi/3))$ の頂点$p$を$e=(\sin(\pi/3),-\cos(\pi/3))$方向に$t>0$だけ摂動してできる三角形領域$T^t$における固有関数$u_2^t,u_3^t$を正しく数値計算する例を与える．

アルゴリズム

以下のアルゴリズムで正しく$u_2^t,u_3^t$を数値計算することができる：

1. 正三角形領域$ T^0$ において，通常の有限要素法で近似固有関数求めて，$\phi_2,\phi_3$とする．
2. 摂動された三角形領域$ T^t$ において，通常の有限要素法で近似固有関数求めて，$\tilde \phi_2,\tilde \phi_3$とする．
3. 上で求めた$\phi_2,\phi_3$と$\tilde \phi_2,\tilde \phi_3$をつかって定理１に現れる行列$M_t,N_t$を求める．
4. 固有値問題$M_t\sigma = \mu N_t\sigma$を解いて固有対$(D_t\lambda_i,\sigma_i)$ $ (i=2,3)$を計算する．
5. 摂動された三角形領域$ T^t$ における現状の近似固有関数$\tilde \phi_2,\tilde \phi_3$を次式を用いて補正する：
   \begin{equation} \tilde u_2^t=s_{22}\tilde \phi_2+s_{23}\tilde \phi_3,~~~~\tilde u_3^t=s_{32}\tilde \phi_2+s_{33}\tilde \phi_3. \end{equation}

数値計算結果

図4は$t=10^{-12},10^{-13},10^{-14},10^{-15}$に対して，摂動された三角形領域$T^t$における固有関数$u_2^t$を数値計算して描画したものである．
ただし，図4の上段は通常の有限要素法を使って求めた近似固有関数，下段は固有値の差分商公式を使って求めた近似固有関数である．
計算にはすべての場合に同じメッシュを用いた．

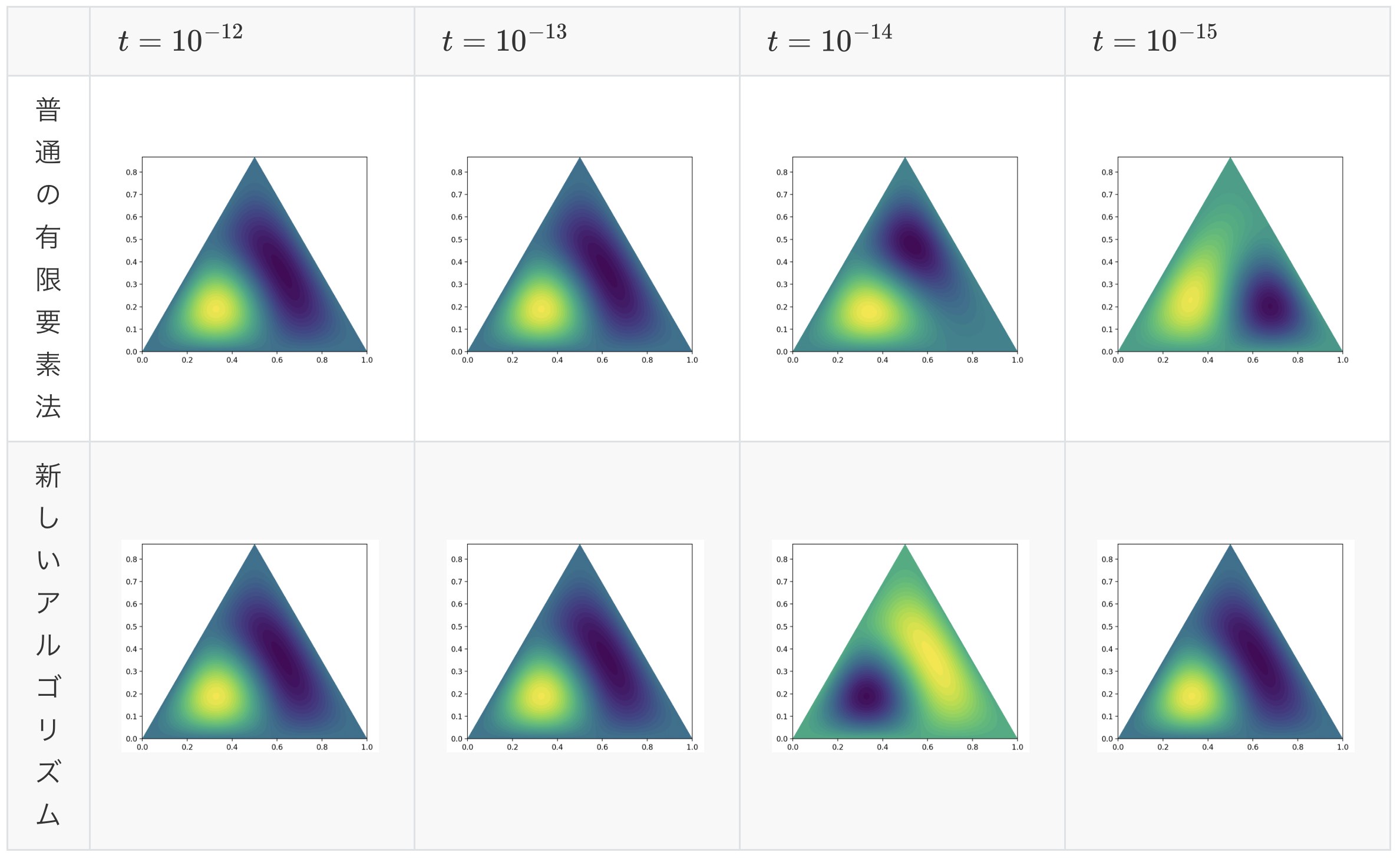求めた近似固有関数

通常の有限要素法による計算では，$t=10^{-14},10^{-15}$あたりで固有関数の回転が起こっているように見えるのに対して，新しいアルゴリズムでは正確に計算できているように見える．
固有値が単純である限り，固有関数は$t$に関して連続に動くはずなので上段の計算結果が正しいということはあり得なさそうである．