院解9 京大数学系H26 基礎II 3 複素積分の値

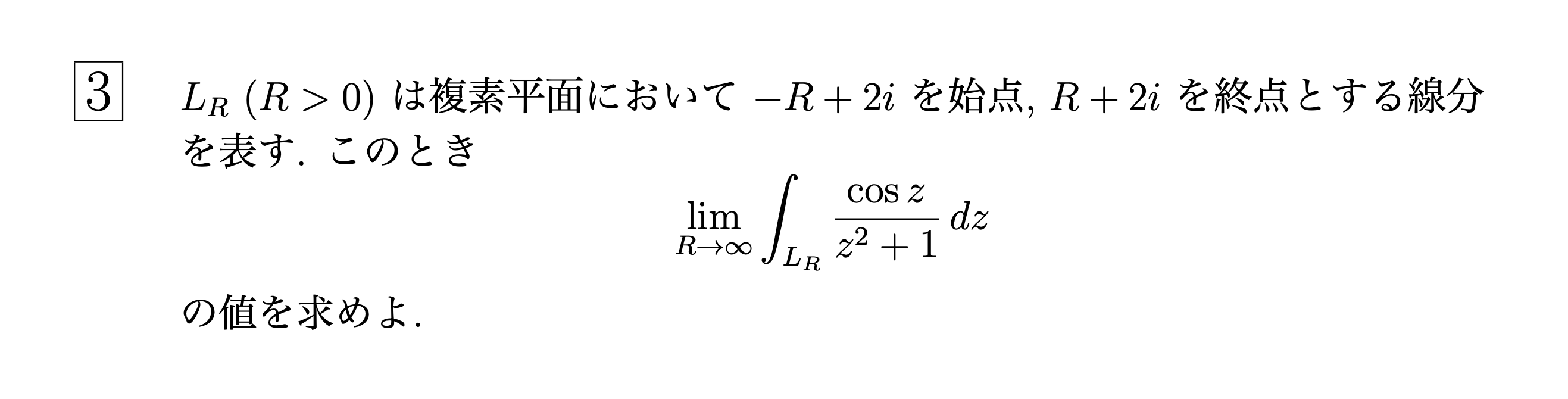
図2のような積分路をとる.

向き付けられた線分$[-R,-R+2i]$上では$R\to\infty$のとき

$\left|\displaystyle\int_{[-R,-R+2i]}\dfrac{\text{cos}z}{z^2+1}dz\right|=\left|\displaystyle\int_0^1 \dfrac{e^{i(-R+2ti)}+e^{-i(-R+2ti)}}{(-R+2ti)^2+1}\cdot 2dt\right|$
$\leq 4e^2\displaystyle\int_0^1 \dfrac{1}{R^2}dt\leq \dfrac{4e^2}{R^2}\to 0\ (R\to\infty).$
$[R+2i,R]$上でも同様.よって$\displaystyle\int_{-\infty}^\infty \dfrac{\text{cos}t}{t^2+1}dt$が存在するとすれば,留数定理から

$(\text{与式})=\displaystyle\int_{-\infty}^\infty \dfrac{\text{cos}t}{t^2+1}dt-2\pi i\text{Res}\left(\dfrac{\text{cos}z}{z^2+1},i\right)$.ここで

$\text{Res}\left(\dfrac{\text{cos}z}{z^2+1},i\right)=\dfrac{\text{cos}i}{4i}=\dfrac{e^{-1}+e}{4i}$.さらに

$\displaystyle\int_{-\infty}^\infty \dfrac{\text{cos}x}{x^2+1}dx=\frac{\pi}{e}$であることは次のようにわかる.

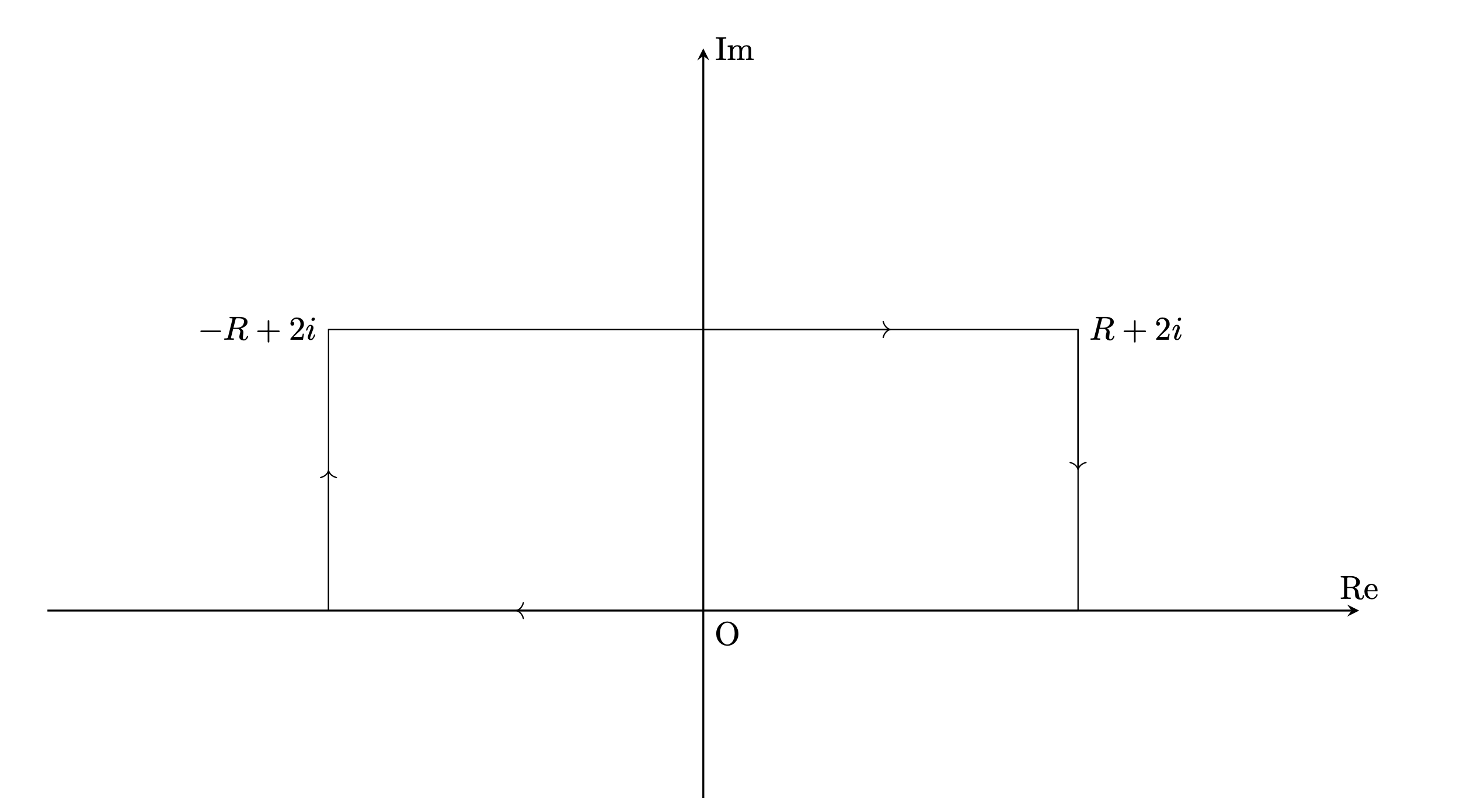
$f(z)=\dfrac{e^{iz}}{z^2+1}$とおき,図3の積分路を取る.

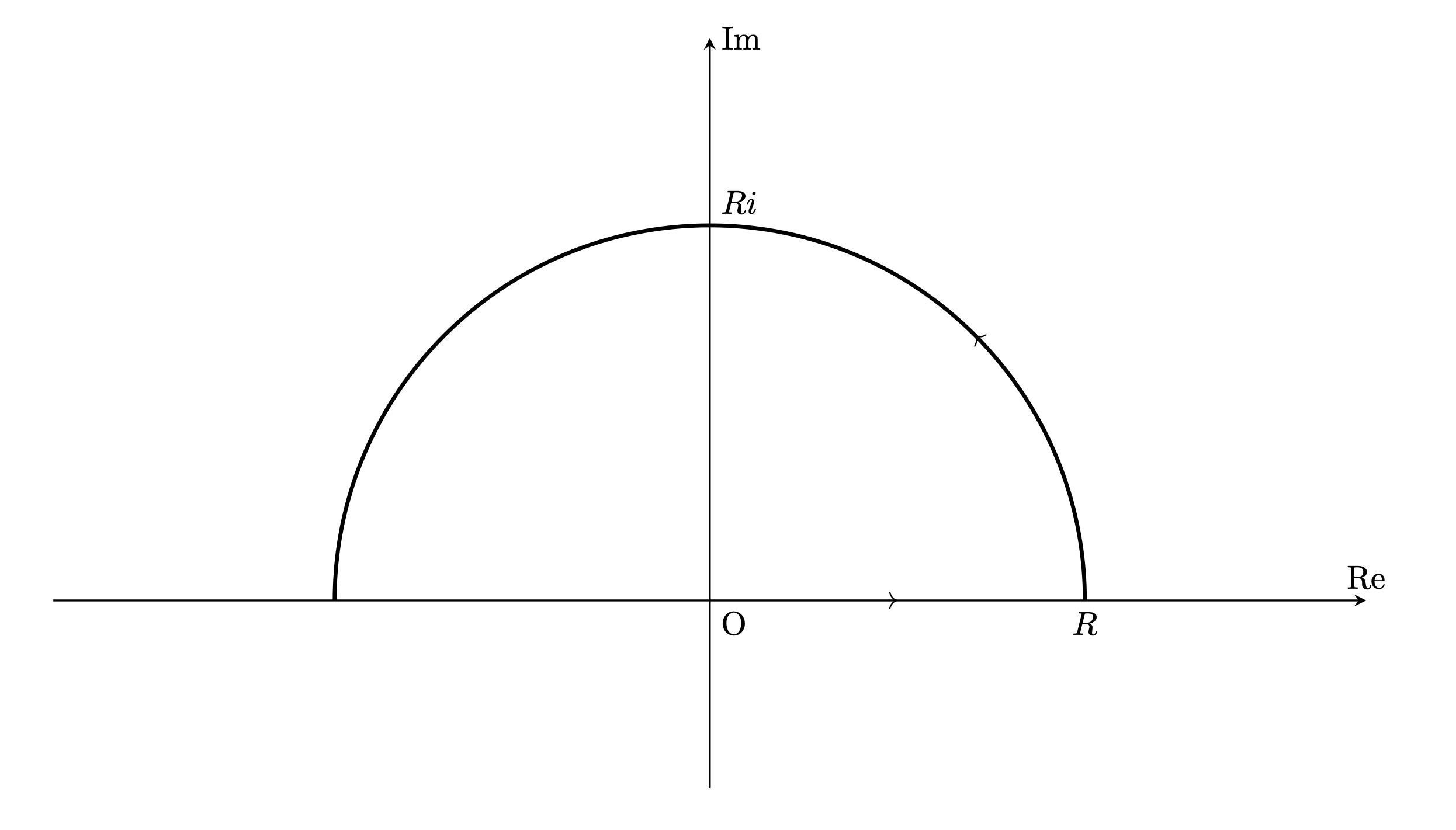
$z=a+bi$として$b\geq 0$で$e^{i(a+bi)}\leq1 $.よって積分路の半円の部分,線分の部分をそれぞれ$\Gamma_1 $,$\Gamma_2$とおくと

$\left|\displaystyle \int_{\Gamma_1} f(z)dz\right|\leq \displaystyle\int_0^{\pi} \left|\dfrac{R}{R^2e^{2it}+1}\right|dt\leq \dfrac{\pi}{R}\to 0\ (R\to\infty)$.
よって留数定理から
$\displaystyle\int_{-\infty}^\infty \dfrac{\text{cos}x}{x^2+1}dx=2\pi i\dfrac{e^{-1}}{2i}=\dfrac{\pi}{e}$.
よって$\dfrac{\pi}{e}-2\pi I\dfrac{e^{-1}+e}{4i}=\dfrac{\pi}{2e}-\dfrac{\pi e}{2}$.$\Box$