automatic sequences

こんにちは,itouです.今回はautomatic sequenceについて解説します.

導入

automatic sequence(k-automatic sequenceともいう)とは,非負整数$n$を基数を$k$として位取り基数法で表示した際に,その数列を入力として受け取る有限オートマトンの出力の列$s(n)$のことをいいます.例を見てみましょう.

Thue Morse sequence

2状態$q_1,q_2$しかとれないオートマトンを考えます.遷移関数$\delta :\{q_1,q_2\}\times \{0,1\}$を以下のように与えます.

出力関数$\tau :\{q_1,q_2\}\to \{a,b\}$を$\tau (q_1)=a,\tau (q_2)=b$,初期状態を$q_1$,生成される数列を$s(n)$とします.$n$を2進数で表記した数列を入力します.

$n=0=0_2$のとき,$s(0)=\tau (q_1)=a$
$n=1=1_2$のとき,$s(1)=\tau (\delta (q_1,1))=b$
$n=2={10}_2$のとき,$s(2)=\tau (\delta (\delta (q_1,0),1))=\tau (q_2)=b$
$n=3={11}_2$のとき,$s(2)=\tau (\delta (\delta (q_1,1),1))=\tau (q_1)=a$
$n=4={100}_2$のとき,$s(4)=\tau (\delta (\delta (\delta (q_1,0),0),1))=\tau (q_2)=b$

同様に,

$s(n{)}_{n\ge 0}=a,b,b,a,b,a,a,b\cdots$

この数列はThue-Morse数列として知られています.2進数で数列を入力してので,これを2-atomaticといいます.

このautmaticな数列の生成手順をグラフで表すと,以下の通りです.

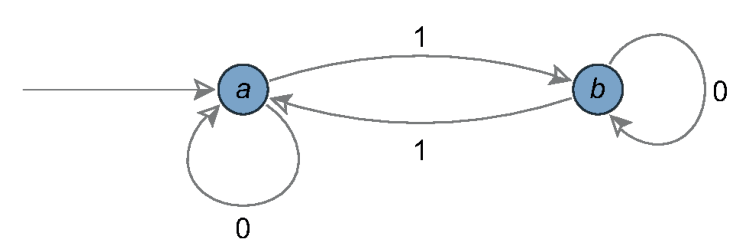例1

別の生成方法

上の数列は以下の方法でも作ることができます.
まず$ab$を用意し,「次の列を$a\to ab,b\to ba$としてもとの列に付け加える」操作を繰り返します.
$$\begin{array}{rl}a& \to ab\\ & \to abba\\ & \to abbabaab\\ & \to abbabaabbaababba\\ .\\ .\\ .\end{array}$$

この操作の極限としてThue Morse sequenceを得ることができます.この数列は操作「次の列を$a\to ab,b\to ba$としてもとの列に付け加える」(変換$a\to ab,b\to ba$をmorphismといいます)の固定点です.固定点については,次のことが知られています.

さて,次のような問題が気になります.

1912年にThueが以下のことを示しました.

実際,Thue-Morse数列がそのような例です.

数論における応用

automatic sequenceは数論に応用されます.以下の定理は重要です.

例えばThue-Morse数列の$a,b$をそれぞれ$0,1$におきかえた数列$s(n{)}_{n\ge 0}=0,1,1,0,\cdots ,y=\sum _{n\ge 0}s(n)x^n$について,
$$\begin{array}{r}(1+x{)}^3{y}^2+(1+x^2)y+x=0\end{array}$$
を満たします.(${\mathbb{F}}_2(x)$において)

定理2より,$\mathbb{Q}(x)$で代数的関数$\sum _{n\ge 0}S(n)x^n$に対し,
$$\begin{array}{r}\sum _{n\ge 0}(S(n)\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{p}){\mathrm{x}}^{\mathrm{n}}\end{array}$$
は${\mathbb{F}}_p(x)$上で代数的関数なので,$(S(n)\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{p}{)}_{\mathrm{n}\ge 0}$はp-automaticです.例えば,カタラン数$C(n)=(\genfrac{}{}{0ex}{}{2n}{n})/(n+1)$を係数にもつ冪級数$y$は
$$\begin{array}{r}x{y}^2-y+1=0\end{array}$$
を満たす代数的関数なので任意の素数$p$について,$C(n)\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{p}$を計算することでp-automaticな数列を生成することができます.
例えば$p=3$のときは3進数数列を入力として受け取るオートマトン:

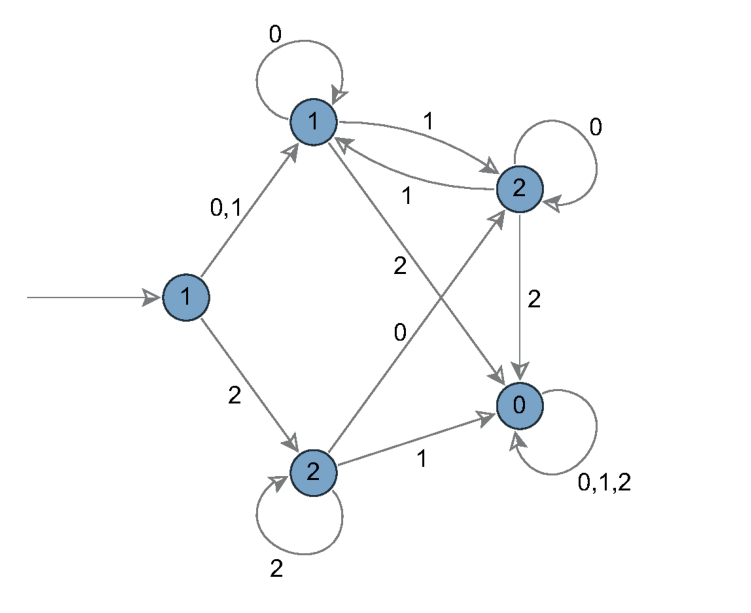例2
が対応します.

$p^a$の場合

$\mathrm{m}\mathrm{o}\mathrm{d}{\mathrm{p}}^{\mathrm{a}}$での数列の場合を考えます.$a\ge 2$のときは Christolの定理を適用できませんが,Furstenbergはrational seriesの
diagnalsを用いることで$p^a$の場合のオートマトンを計算することができることを示しました.

例えばカタラン数がdiagnolの係数に現れる有理関数は
$$\begin{array}{r}\frac{(y+1)(2x{y}^2+xy+x-1)}{x{y}^2+2xy+x-1}\end{array}$$
であり,これにより,カタラン数のautomationを計算したり,カタラン数の合同式を得ることができます.例えばすべての正整数$n$について$C(n)\not\equiv 3\mathrm{m}\mathrm{o}\mathrm{d}4$
であることが分かります.

この手法は代数的関数だけでなく,有理関数のdiagnalに対して適用されるので,代数的関数でない関数にも応用することができます.例えばアペリー数$A(n)=\sum _{k=0}^n{(\genfrac{}{}{0ex}{}{n}{k})}^2{(\genfrac{}{}{0ex}{}{n+k}{k})}^2$については
正整数$n$を$n=n_l{n}_{l-1}\cdots n_0$と基数$p$で位取り基数法で表したとき,
$$\begin{array}{r}A(n)\equiv {\mathrm{\Pi }}_{i=0}^{l}A(n_i)\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{p}\end{array}$$
が成立します.(Gessel)

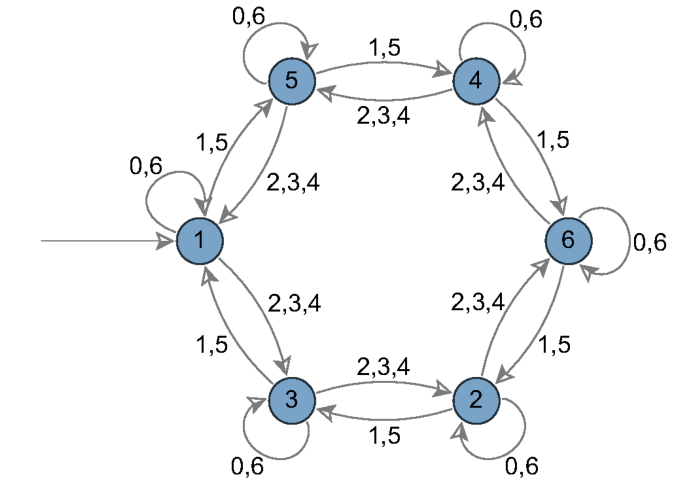法7でのアペリー数のautomation

感想

autmationについて調べるモチベができたのでやってみました.

謝辞

誤植指摘等よろしくお願いいたします.