群の定義の単位元の公理を少し変えると…
群の定義について
ある集合の任意の2つの元から同じ集合のある元が定まるようなものを考えて、代数系と呼ぶ。特に汎用性の高くて最も基本とされて最初に引き合いに出される「群」という代数系がある。
時々ネットで話題になる「群の定義」で、昨年ある件で話題になった時考えてみたことについて思い出したので書く。
その時の自分のXの投稿
群の定義
集合$G$が群であるとは、二項演算$ \cdot $が定義されていて、$g_1,g_2 \in G$の演算結果を積と呼び$g_1 \cdot g_2$で表すとき以下の性質をもつことである。
- 閉じていること
$ \forall g_1,\forall g_2 \in G ; g_1 \cdot g_2 \in G$ - 結合律の成立
$\forall g_1,\forall g_2 ,\forall g_3 \in G ;g_1 \cdot (g_2 \cdot g_3)=(g_1 \cdot g_2) \cdot g_3$ - 単位元の存在
$ \exists e\in G;\forall g \in G; e \cdot g = g \cdot e =g$
$e$は$G$の単位元と呼ぶ - 逆元の存在
$e$は3によって存在する単位元とするとき、
$ \forall g \in G;\exists g' \in G; g \cdot g'=g' \cdot g = e $
この$g'$を$g$の逆元といって$g^{-1}$で表す
余談として、上記の1まで満たす代数系を
マグマ
、2まで満たすものを
半群
、3まで満たすものを
モノイド（単位的半群）
という。
よって
群
は各元に逆元があるモノイドである。
単位元の公理について
昨年話題になっていたのはある物理の本で、単位元の存在の公理について、
3(?).単位元(?)の存在
$ \forall g \in G;\exists e\in G;$ $ e \cdot g = g \cdot e =g$
11/7 再修正 指摘をいただいたので修正
$g$に依存するので一意に定まらない。このような単位元全体の集合を$E_g$とする。
$E_g:=\{e \in G| e \cdot g = g \cdot e =g\}$
「任意の元の」が先に書かれていて、単位元が元$g \in G$に依存するように誤解してしまうのではないかというものだった。（他の事についても話題になっていたが今回はそれは触れない。）
実際それだと、本来群にならないものも「群」になってしまう
追記
単位元が一意ではないので逆元の存在の公理についても少し修正する。
4(?). 逆元(?)の存在
$ \ \ E_g$を3(?)によって$g$に対して存在する単位元集合とするとき、
$ \ \ \forall g \in G;\exists e \in E_g;\exists g' \in G; g \cdot g'=g' \cdot g = e $
逆元についても一意とは限らない。
整数の2元集合{0,1}と"かけ算"
集合$ G=\{0,1\} $に積を以下で定義する。
$0 \cdot 0 =0$
$0 \cdot 1 =0$
$1 \cdot 0 =0$
$1 \cdot 1 =1$
閉じている
結果も$ G $の元なので閉じている。
結合律
通常のかけ算と同じなので、結合律も満たしている。
単位元(?)と逆元の定義
$0$の単位元と逆元を$0$
$1$の単位元と逆元を$1$
と定義する。
単位元(?)の存在公理3(?)
$ \forall g \in G;\exists e\in G;$ $ e \cdot g = g \cdot e =g$
について
$0 \cdot 0 =0$
$1 \cdot 1 =1$
なのだから、
3(?)を満たしている。
逆元
逆元(?)の存在公理4(?)
$ \ \ \forall g \in G;\exists e \in E_g;\exists g' \in G; g \cdot g'=g' \cdot g = e $
も同じ式
$0 \cdot 0 =0$
$1 \cdot 1 =1$
より満たしているとわかる。
結果
よって、間違った定義の下ではこの代数系は（無理があるが）群になってしまう。
乗積表では
| ・ | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
となる。
もちろん本来の適切な定義では、単位元を1とできるが、0の逆元が存在しないので適切な定義では「群」にはならない。
乗積表を見ると、これは$0$は偽、$1$は真を表すとしたときの論理積演算である。
{0,1}と別の演算（論理和）
同じ集合$G=\{0,1\}$と論理和の演算ではどうなのか。
| or | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
（追記）間違った定義の場合、かけ算の時の定義2と同様に$g$の単位元も逆元も$g$とすることにすると、
$0 \ or \ 0=0$
$1 \ or \ 1=1$
なので、3(?)単位元(?)の存在、4(?)逆元の存在(?)を満たしているので、群(?)になってしまう。
しかし、適切な定義3、4の場合、
単位元は、$0$とできるが、今度は$1 $との演算結果は$1$になってしまい単位元$0$にはならないため$1$の逆元が存在しない。
適切な定義では「群」にはならない。
{0,1}と別の演算（排他的論理和）
同じ集合$G=\{0,1\}$と排他的論理和の演算ではどうなのか。
| xor | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
$0 \ xor \ 0 =0$
$1 \ xor \ 0 =0 \ xor \ 1 =1$
単位元は$0$とできることが分かった。
$0 \ xor \ 0 =0$
$1 \ xor \ 1 =0$
$g$逆元は$g$自身でよいことが分かった。
適切な定義でもちゃんと「群」になる。
これは、通常のたし算結果を$2 $で割った余りの群、$2$元巡回群$ \mathbb{Z} /2 \mathbb{Z}$と同型の群である。
この演算をたし算として、$0$を除くと$1$のみの集合$\{1\}$で$1 \times 1 =1$なので、かけ算も入れて$1$の逆元は$1$で、
有限体$ \mathbb{F}_2$
となることも確かめられる。
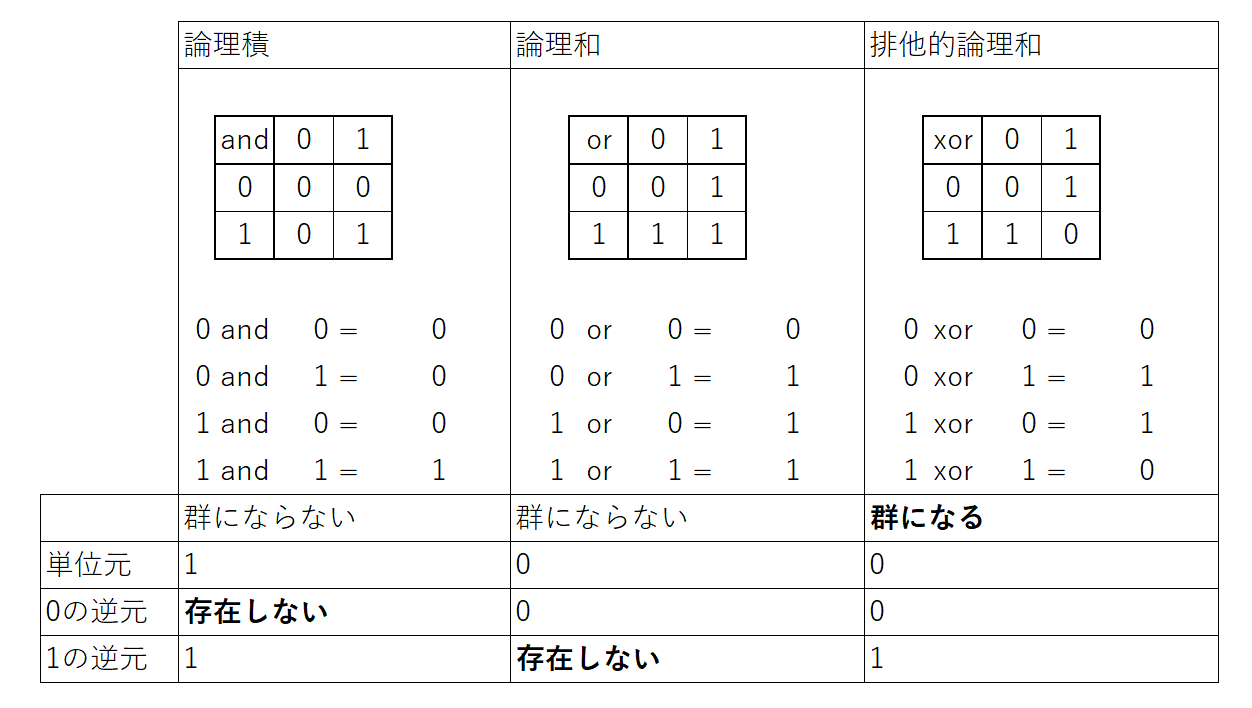論理演算が群になるか
余談
この時、この話題が起点となって、群論の高名な専門家が書いた本に載っているという群の定義も話題になっていた。
空でない集合$G$で、二項演算が定義されていて、
- 任意の3元が結合律を満たす
- 任意の2元$a,b $に対して方程式 $ax=b $ と $ya=b $の解$x,y $が$G$の中に存在する
このときGが群になるという。
という単位元と逆元という言葉が出てこない定義も面白いと思ったので、この定義から、この記事の最初に書いた定義の命題（通常よくある群の定義）を満たしていることを考えたりした。
→そのときの自分のXの投稿
おわりに
(指摘度修正)
間違った定義だと、適切な定義では「群」にならないもの（{0,1}と論理積、{0,1}と論理和）まで、群(?)となってしまう。
もちろんこれらは本来の群（同じ集合の置換の集合に合成で演算を入れたものと同じ構造）にはならない。
そもそも、公理がぶつからないように例を作る場合も適切な群にする場合も、逆元の公理も大きく修正することになってしまい定義に無理があるものになってしまったので、単位元の存在公理も誤解がない記述が望ましいことが分かった。
群の定義については、ネットで時々話題になっている。最近も別件（逆元の公理で群の定義をしている最中なのに単位元eが使われるのに違和感があるとかで？）で話題になっていた。
話題になるたびに例や反例などを考えてみることで、多くない知識でも一人遊びができて楽しむことができる。数学ならではの楽しみ方だと思う。
