【図形】調和平均と台形

はじめに

二つの数の平均を求める方法の１つに調和平均という求め方があります。よく聞く平均の種類は相加平均、相乗平均かと思いますが、調和平均とはどのような平均なのでしょうか。
（調和平均については別途まとめたいと思います。）

調和平均

この記事では調和平均を台形の中から探してみます。下図のような台形$ABCD$を考えることとします。$線分AB /\!/ 線分DC$で線分$AB$の長さは$a$、線分$DC$の長さは$b$です。
台形$ABCD$

ここで唐突ですが、台形$ABCD$の対角線$AC$と$BD$の交点を$H$とします。そして点$H$をとおり線分$AB$と並行な直線を考え、線分$AD$、$BC$との交点をそれぞれ$I$、$J$とします。すると、なんと線分$IJ$が調和平均の値となるのです。
台形$ABCD$（補助線つき）

線分$IJ$の値を確かめてみる

線分$IJ$の確認1
$\triangle ACD$と$\triangle AHI$について、$\angle CAD = \angle HAI$です。$線分CD /\!\ 線分HI$より同位角は等しいので、$\angle ACD = \angle AHI$、$\angle ADC = \angle AIH$となります。これより３つの角がそれぞれ等しいことが分かったので、$\triangle ACD \backsim \triangle AHI$となります。このことより$CD:HI=AC:AH$ですが、この時点でわかっていることは$CD=b$ということだけです。

線分$IJ$の確認2
別の三角形$\triangle ABH$と$\triangle CDH$を見てみましょう。対頂角は等しいので$\angle AHB = \angle CHD$です。また$線分AB /\!\ 線分DC$より錯角は等しいので、$\angle ABH = \angle CDH$、$\angle BAH = \angle DCH$です。３つの角がそれぞれ等しいことが分かったので、$\triangle ABH \backsim \triangle CDH$となります。これより$AH:CH=AB:CD=a:b$ということが分かりました。

$AH:CH=a:b$より$AH:AC=AH:(AH+HC)=a:(a+b)$です。先ほどの$\triangle ACD$と$\triangle AHI$に戻ってみると、$CD:HI=AC:AH$より$b:HI=AC:AH=(a+b):a$、よって$HI=\frac{ab}{a+b}$となります。$\triangle BCD$と$\triangle BJH$で同様に考えてみると、$HJ=\frac{ab}{a+b}$となります。よって線分$IJ=IH+JH=\frac{ab}{a+b}+\frac{ab}{a+b}=2\frac{ab}{a+b}$となり、調和平均の値となることを導くことができました。
線分$IJ$の確認3

相加平均と調和平均

相加平均も台形の中にあることが分かります。見つけ方は 【図形】相加相乗平均と台形 を参照ください。調和平均と相加平均を台形の中に見つけることができたので、２つの平均を図示してみます。図から見て分かるとおり「調和平均$\leq$相加平均」となることが分かります。数式を変形していくことによっても導くことができますが、図形を利用すると視覚的に捉えることができ分かりやすいですね。
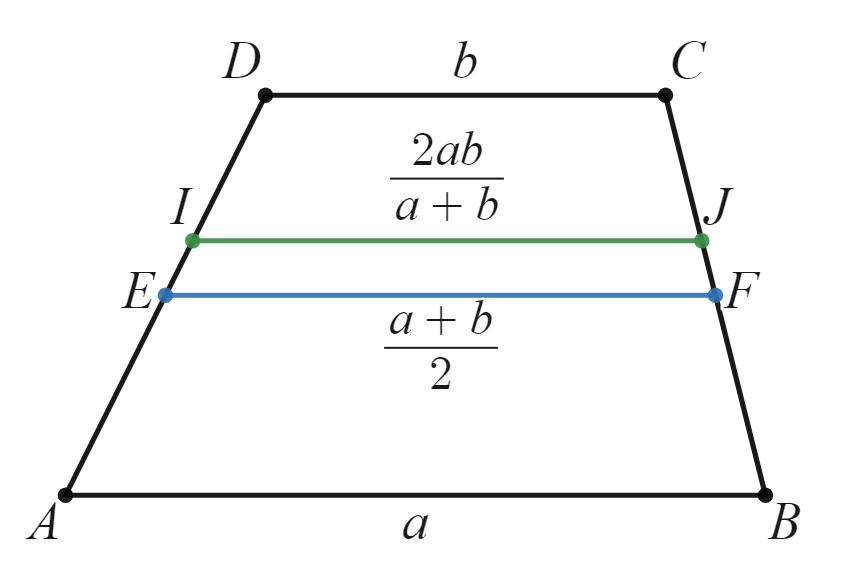台形の中にある調和平均と相加平均

まとめ

台形の中に調和平均を見つけることができ、相加平均との大小関係も視覚的に捉えることができました。調和平均の式はぱっと見、少し複雑そうに見えますが、このように台形の中にきれいに現れるのですね。