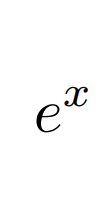分数階微積分入門[2] ~分数階微分の定義~
この記事では
分数階微積分入門[1] ~ 分数階積分の定義 ~
の続きになってます. 前回は分数階積分を定義したので次に微分の方を定義していきます. 実は分数階積分を定義すれば微分の方は簡単に定義できます.
分数階微分のアイデア
次の定理が分数階微分を定義する上でアイデアである.
$m, n \in\mathbb{N}$, $m>n$ とし, $f\in C^\infty([a, b])$ とする. このとき,$D^n = D^m J_a^{m-n}$ が成立する.
微分積分学の基本定理 から, $f = D^{m-n}J^{m-n}$ である. この両辺に微分作用素 $D^n$ 作用させ, $D^nD^{m-n}=D^m$に注意すれば,
$D^n f = D^nD^{m-n}J_a^{m-n}f = D^{m}J_a^{m-n}$ を得る.
分数階積分は前回定義したので, 上の定理を使えば上手く微分が定義できることがわかる. 分数階積分は以下のように定義した.
$n \in \mathbb{R}_{+}$ とする. 作用素$J_{a}^{n}$を$L^1[a,b]$において次のように定義する.
\begin{equation}
J_a^n f(x) = \frac{1}{\Gamma(n)} \int_a^x (x-t)^{n-1} f(t) dt
\end{equation}
Riemann-Liouville$n$階積分とよぶ. $n=0$に対しては, $J_a^0 = I$ とする. ただし, $I$は恒等写像とする.
分数階微分
分数階微分を以下のように定義する.
$n \in \mathbb{R}_{+}$とする. 作用素 $D_{a}^{n}$ を $D_a^n f = D_a^m J_a^{m-n}f$ と定める. つまり,
\begin{eqnarray}
D_{a}^{n}f(x) = \frac{1}{\Gamma(m-n)}\frac{d^m}{dx^{m}} \int_a^x (x-t)^{m-n-1}f(t) dt
\end{eqnarray}
これをRiemann-Liouvilleの分数階微分とよぶ. ここで $m-1< n< m,\ m\in\mathbb{N}$. $n=0$ に対しては $D_a^0=I$, として恒等作用とする.
注意
定理1では$n< m$を満たす自然数$m$ならどれでもいいが, 今回は$n< m$を満たす最小の自然数を選択した. 実はどのように$m$選択しても結果は変わらないことがわかっている.
具体的な計算例
$-1<\beta, n>0$ とし, 自然数$m$を $m-1< n< m$ 満たすものとする. $f(x)=(x-a)^\beta$としたとき, $D_a^nf(x)$を求めよ.
前回の例1から,
$ D_a^n f(x) = D_a^m J^{m-n}f(x) = \frac{\Gamma(\beta + 1)}{\Gamma(m-n + \beta + 1)} D_a^m[(x-a)^{m-n+\beta}].$
特に, $n-\beta \in\mathbb{N}$ のときは右辺の$(x-a)^{m-n+\beta}$ の次数は$m$ 以下なので, $D^{m}[(x-a)^{m-n+\beta}] = 0$. 一方, $n-\beta\not\in\mathbb{N}$ なら,
$ D_a^n f(x) = \frac{\Gamma(\beta+1)}{\Gamma(\beta+1-n)}(x-a)^{\beta - n}$ となる.
なのでこれは古典論と一致しているのがよくわかる.
最後に
今回は簡単な分数階微分の計算をしてみました. このように上手く古典論と一致しているのがよくわかるのですが, 全てが上手くいくわけではありません. 例えば定数関数を微分したとき, 古典論では$0$になるはずですが, $1/2$階微分したものは$0$にはなりません. 余裕がある人は手を動かしてしてみましょう.
さて, 分数階微分まで定義しましたが, ここで記事が終わるのは面白くないのでもう少し続けようと思います. 次回は$e^x$の微分などを計算してみようと思います. その計算は定義通りにしようとすると上手くいかない(原始関数がが初等関数で表せない)ので少し工夫が必要です. それは次回に回しましょう.
ちょっと今回は短くなりましたが, 次回は少し重く?なります. 次々回は分数階微分方程式を予定しています. それでは.