Dyck路とピークに印を付けたDyck路の数え上げ
長さ$2n$のDyck路の集合から$n$個の$U$と$n+1$個の$D$からなるネックレス(高校数学でいう円順列のこと)の集合への全単射を与えます.後者の集合のサイズは容易に求まるので,これにより長さ$2n$のDyck路の総数を求めることができます.
また,ピークに印を付けた長さ$2n$のDyck路の集合から$n-1$個の$U$と$n$個の$D$からなるワードの集合への全単射を与え,ピークに印を付けた長さ$2n$のDyck路の総数が$\binom{2n-1}{n}$であることのbijective proofを与えます.
Dyck路とネックレスの対応
$xy$平面における$(0, 0)$から$(2n, 0)$への経路で,各ステップが$U:=(1, 1)$または$D:=(1, -1)$からなり,$x$軸より下を通らないものを長さ$2n$のDyck路という.長さ$2n$のDyck路には$n$個の$U$と$n$個の$D$からなるワードが自然に対応する.これをDyckワードという.
以下ではDyck路と対応するDyckワードを断りなく同一視します.またDyck路を$w$で表します.
長さ$6$のDyck路は以下の$5$個である.

それぞれに対応するワードは$UDUDUD$,$UDUUDD$,$UUDUDD$,$UUDDUD$,$UUUDDD$である.
Dyck路の$UD$という形の部分列をピークという.
$w,v = a_1 a_2 \cdots a_l$を二つのワードとする.ただし$a_1, a_2, \cdots, a_l$は文字である.ある巡回置換$\sigma \in \langle (1, 2, \cdots, l) \rangle $が存在して$w = a_{\sigma (1)} a_{\sigma (2)} \cdots a_{\sigma (l)}$であるとき,$w \sim v$と定める.この同値関係$\sim$により定まるワードの同値類$[w]$をネックレスという.
$n \geq 0$に対し,$n$番目のCatalan数を
\begin{equation}
C_n = \cfrac{1}{n+1} \binom{2n}{n}
\end{equation}
で定義する.
長さ$2n$のDyck路の集合を$D_n$,$n$個の$U$と$n+1$個の$D$からなるネックレスの集合を$N_n$,$n$個の$U$と$n$個の$D$からなるワードの集合を$W_n$とする.
(1) $f_1 (w) = [wD]$で定まる写像$f_1 \colon D_n \to N_n$は全単射である.
(2) $f_2 (w) = [wD]$で定まる写像$f_2 \colon W_n \to N_n$は$n+1$対$1$である.
(3) $|D_n| = |N_n| = C_n.$
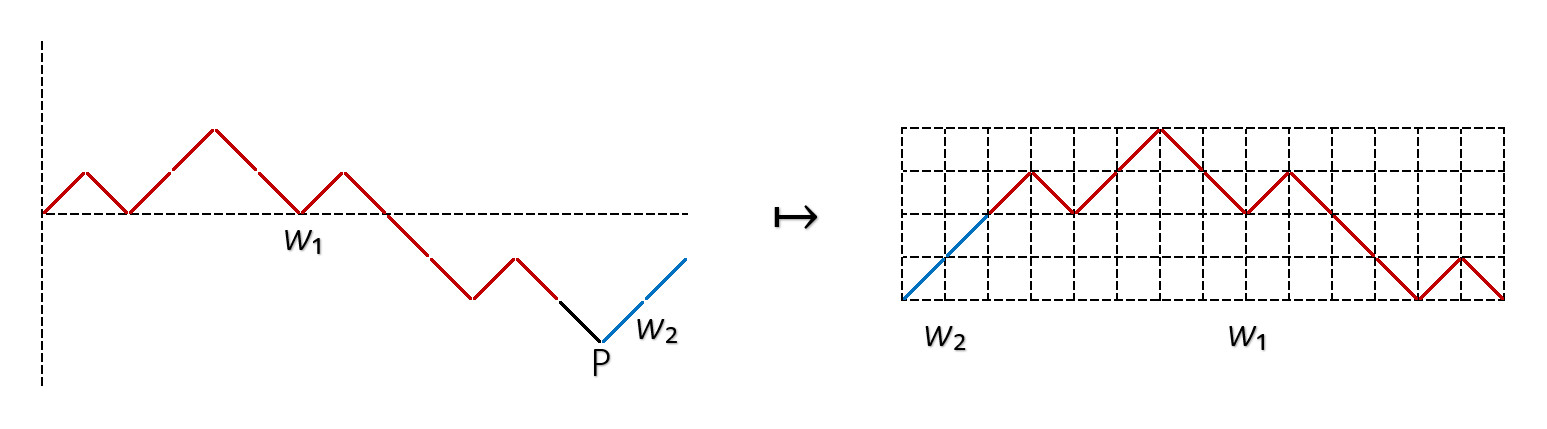
- 写像$g_1 \colon N_n \to D_n$を以下で定める.$[w] \in N_n$とする.$w$を$xy$平面における原点から出発する経路と同一視する.$w$における$y$座標が最も小さい点で最も左にあるものを$P$とする.$w$を原点から点$P$までの経路$w_1 D$と点$P$以降の経路$w_2$に分ける.このとき$g_1 ([w]) = w_2 w_1$と定める.この写像$g_1$はwell-definedであり,$f_1$の逆写像となることがわかる.
- $n$個の$U$と$n$個の$D$と$1$個の$X$からなるネックレスの集合を$M_n$とする.$g_2 (w) = [wX]$で定まる写像$g_2 \colon W_n \to M_n$は明らかに全単射である.また$X$を$D$へ置き換えることで定まる写像$g_3 \colon M_n \to N_n$は明らかに$n+1$対$1$である.$f_2 = g_3 \circ g_2$より,$f_2$は$n+1$対$1$である.
- (1)より$|D_n| = |N_n|$.また(2)より$|N_n| = \cfrac{1}{n+1} |W_n| = C_n$.
ピークに印を付けたDyck路とワードの対応
$w$をDyck路とする.$w$のあるピーク$U D$を$U \bullet D$に置き換えたワードを$\widehat{w}$で表し,ピークに印を付けたDyck路という.$\widehat{w}$は$w$のある部分列$w_1,w_2$を用いて$\widehat{w} = w_1 U \bullet D w_2$と表すことができる.$\widehat{w}$のピークに印を付けたDyck路としての長さを$w$の長さで定める.
ピークに印を付けたDyck路$\widehat{w}$のワードとしての長さは$(w\text{の長さ})+1$である.
ピークに印を付けた長さ$6$のDyck路は以下の$10$個である.

ピークに印を付けた長さ$2n$のDyck路の集合を$\widehat{D}_n$,$n-1$個の$U$と$n$個の$D$からなるワードの集合を$V_n$とする.
(1) $f(w_1 U \bullet D w_2) = w_2 D w_1$で定まる写像$f \colon \widehat{D}_n \to V_n$は全単射である.
(2) $|\widehat{D}_n| = |V_n| = \binom{2n-1}{n}.$
- 定義5を一般化し,$U$と$D$からなるワード$w$のある部分列$U D$を$U \bullet D$に置き換えたワードを$\widehat{w}$で表し,その同値類$[\widehat{w}]$をピークに印を付けたネックレスということにする.$n$個の$U$と$n+1$個の$D$からなるピークに印を付けたネックレスの集合を$\widehat{N}_n$とする.定理1(1)の全単射$f_1$は,Dyck路のピークとネックレスのピークの$1$対$1$対応を与えるから,$g(w_1 U \bullet D w_2) = [w_1 U \bullet D w_2 D]$で定まる写像$g \colon \widehat{D}_n \to \widehat{N}_n$は全単射である.一方$h([w_1 U \bullet D w_2]) = w_2 w_1$で定まる写像$h \colon \widehat{N}_n \to V_n$は明らかにwell-definedかつ全単射である.$f = h \circ g$より,$f$は全単射である.
- (1)より$|\widehat{D}_n| = |V_n|$.また$|V_n| = \binom{2n-1}{n}$は明らかである.
