0
大学数学基礎解説
東大数理院試過去問解答例(2006B08)
194
0
$$$$
ここでは東大数理の修士課程の院試の2006B08の解答例を解説していきます。解答例はあくまでも例なので、最短・最易の解答とは限らないことにご注意ください。またこの解答を信じきってしまったことで起こった不利益に関しては一切の責任を負いませんので、参照する際は慎重に慎重を重ねて議論を追ってからご参照ください。また誤り・不適切な記述・非自明な箇所などがあればコメントで指摘していただけると幸いです。
2006B08
$\mathbb{R}^3$の部分空間
$$
Y=\left\{(x,y,z)\in\mathbb{R}^3\middle|9\leq x^2+y^2+z^2\leq16, x^2+z^2\geq1, y^2+z^2\geq1\right\}
$$
をとり、その境界を$X$とする。
- 整係数ホモロジー群$H_\ast(X,\mathbb{Z})$を求めなさい。
- $X$上の同相$f:X\to X$を
$$ f(x,y,z)=(-y,x,z) $$
によって定義する。このとき$\mathbb{Z}$加群の自己準同型$f_\ast:H_1(X,\mathbb{Z})\to H_1(X,\mathbb{Z})$の特性多項式を計算しなさい。
- まず以下の図1のように中身のない円柱を$4$つとり、白でない同じ色の辺を矢印の向きに貼り合わせた位相多様体を考える。これを$Z$とする。
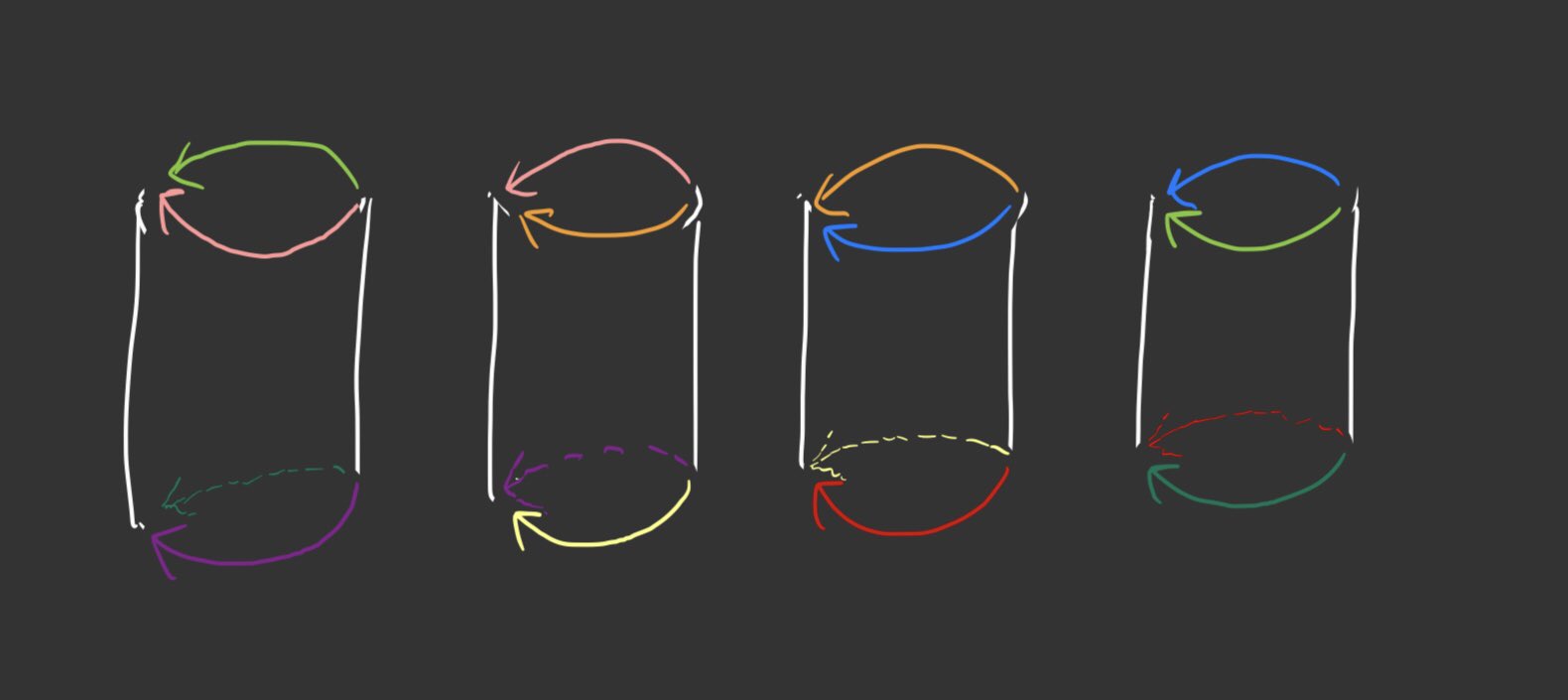
このとき$X$は$Z$にホモトープである。胞体分割を用いて直接計算することで
$$ {\color{red}H_\ast(X,\mathbb{Z})=\begin{cases} \mathbb{Z}&(\ast=0,2)\\ \mathbb{Z}^6&(\ast=1)\\ 0&(\textsf{if else}) \end{cases}} $$
が従う。 - 胞体分割を用いた計算により、$H_1(X,\mathbb{Z})$の生成元をうまくとり、その$f$による像を見ることで、$f_\ast$は表現行列
$$ \begin{pmatrix} 0&0&-1&0&0&0\\ 1&0&-1&0&0&0\\ 0&1&-1&0&0&0\\ 0&0&0&0&0&-1\\ 0&0&0&1&0&-1\\ 0&0&0&0&1&-1 \end{pmatrix} $$
で表されることがわかる。この特性多項式は${\color{red}(X+1)^2(X^2+1)^2}$である。
投稿日:2024年9月20日
更新日:2024年9月20日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中
