復元抽出の超幾何分布

超幾何分布

確率分布には超幾何分布という非復元抽出の確率分布があります。これはヴァンデルモンドの恒等式からでも導出出来ます。
なぜなら畳み込みなので等価となる二項係数を分母として、畳み込みの全ての項を分子とすると$1$になります。
$N＝x＋y$として
超幾何分布の確率質量分布$\frac{ { x \choose i } { y \choose K−i } }{ { N \choose K } }$
青線$x=1$,赤線$x=2$,緑線$x=3$
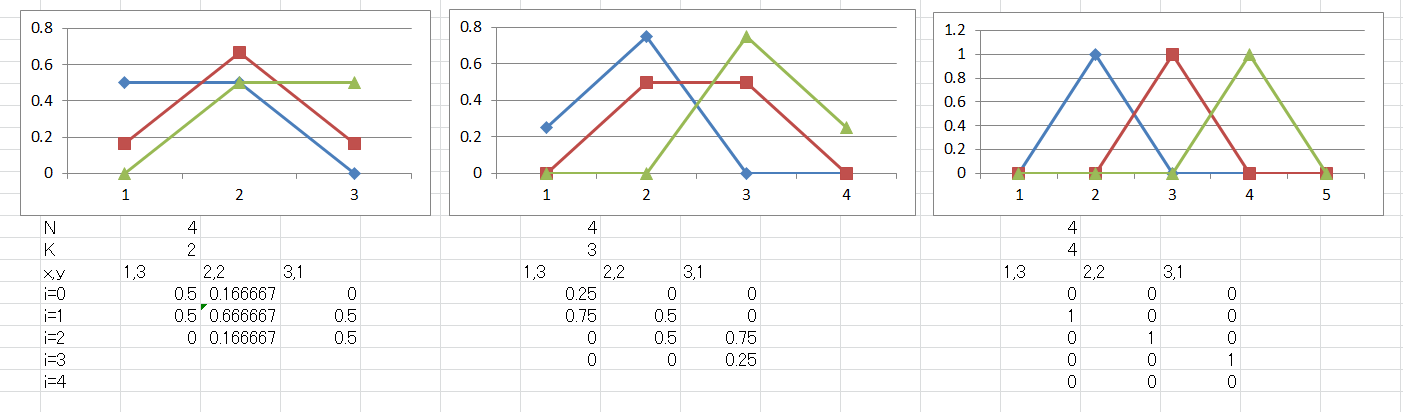超幾何分布

復元抽出の超幾何分布

以前記事にした https://mathlog.info/articles/3770
では重複組合せも同じような畳み込みになることを紹介しました。
復元抽出である重複組合せを超幾何分布のような確率質量分布として扱ってみると、超幾何分布より曲線が緩やかになってました。
$\frac{{ x+i-1 \choose i }{ y+(K-i)-1 \choose (K-i) } }{ { N+K−1 \choose K } }$

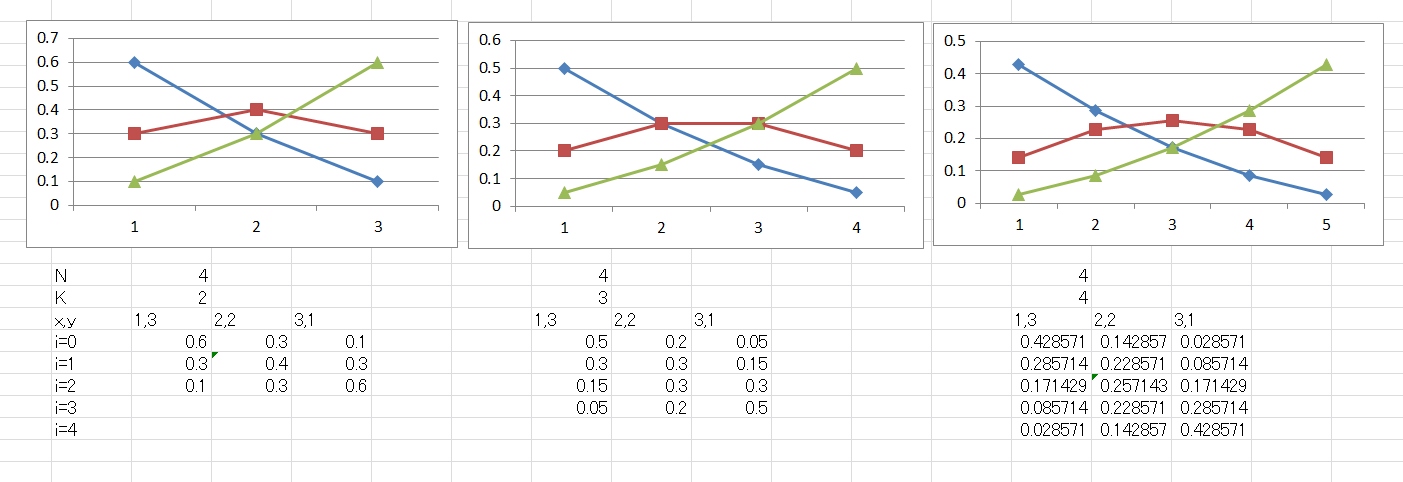復元抽出超幾何分布
しかし超幾何分布は$N$が大きくなるほど二項分布に近づきます。結局、復元抽出の確率分布になっていくわけです。