三角関数と多項式(sinx-x/x^3)の極限の高校生な解法
はじめに
ご機嫌ようです!
今回の記事は短めです!
自分が作問をしてる際に出会った極限のお話です.
解くのは簡単ですが高校生の範囲で解くのが難しかった...
次の極限値を求めよ.
$$\lim_{x\to0}\dfrac{\sin{x}-x}{x^3}$$
答えは$-\dfrac{1}{6}$とロピタルからわかるでしょう.
多項式で$\sin{x}$を挟めばできそうですが次数もだいぶ必要...
これの高校範囲での積分を用いる解法を見つけたので紹介します.
ただここで一つ...お願いです...
$$\lim_{x\to0}\dfrac{\sin{x}}{x}=1$$
は既知とします.させてください.
本題
次の等式を利用します.
先に思いついた方↓(解法1)
$$\sin{x}-x=-\int_{0}^{x}(x-t)\sin{t}dt$$
後から思いついて度肝抜かれた方↓(解法2)
$$\sin{x}-x=\int_{0}^{x}(\cos{t}-1)dt$$
$$\int_{0}^{x}(x-t)\sin{t}dt=\int_{0}^{x}x\sin{t}-t\sin{t}dt$$
$$=x\int_{0}^{x}\sin{t}dt-\int_{0}^{x}t\sin{t}dt$$
$$=x(1-\cos{x})-(\sin{x}-x\cos{x})$$
$$=x-\sin{x}$$
$-1$を両辺にかけると等式を得る.
次の極限値を求めよ.
$$\lim_{x\to0}\dfrac{\sin{x}-x}{x^3}$$
先程の等式から,次のように書き換えられる.
$$\dfrac{\sin{x}-x}{x^3}=-\dfrac{1}{x^3}\int_{0}^{x}(x-t)\sin{t}dt$$
置換$t=xu$と置換すると,$dt=xdu$
積分区間は$0\to1$に変わる.
$$-\dfrac{1}{x^3}\int_{0}^{x}(x-t)\sin{t}dt=-\dfrac{1}{x^3}\int_{0}^{1}(x-xu)\sin{(xu)}\,xdu$$
$$=-\int_{0}^{1}(1-u)\dfrac{\sin{(xu)}}{x}du$$
$$=-\int_{0}^{1}u(1-u)\dfrac{\sin{(xu)}}{xu}du$$
積分区間で次の不等式が成り立つので
$$\dfrac{\sin{x}}{x}\leqq\dfrac{\sin{(xu)}}{xu}\leqq 1$$
次の不等式も成り立つ.
$$-\int_{0}^{1}u(1-u)du\leqq-\int_{0}^{1}u(1-u)\dfrac{\sin{(xu)}}{xu}du\leqq
-\dfrac{\sin{x}}{x}\int_{0}^{1}u(1-u)du$$
$x\to0$とすればはさみうちの原理より,
$$\lim_{x\to0}\dfrac{\sin{x}-x}{x^3}=-\int_{0}^{1}u(1-u)du=-\dfrac{1}{6}$$
を得る.
ちなみに途中で出てきた不等式,
$$-\int_{0}^{1}u(1-u)du\leqq-\int_{0}^{1}u(1-u)\dfrac{\sin{(xu)}}{xu}du\leqq
-\dfrac{\sin{x}}{x}\int_{0}^{1}u(1-u)du$$
はグラフで見るとわかりやすいです.
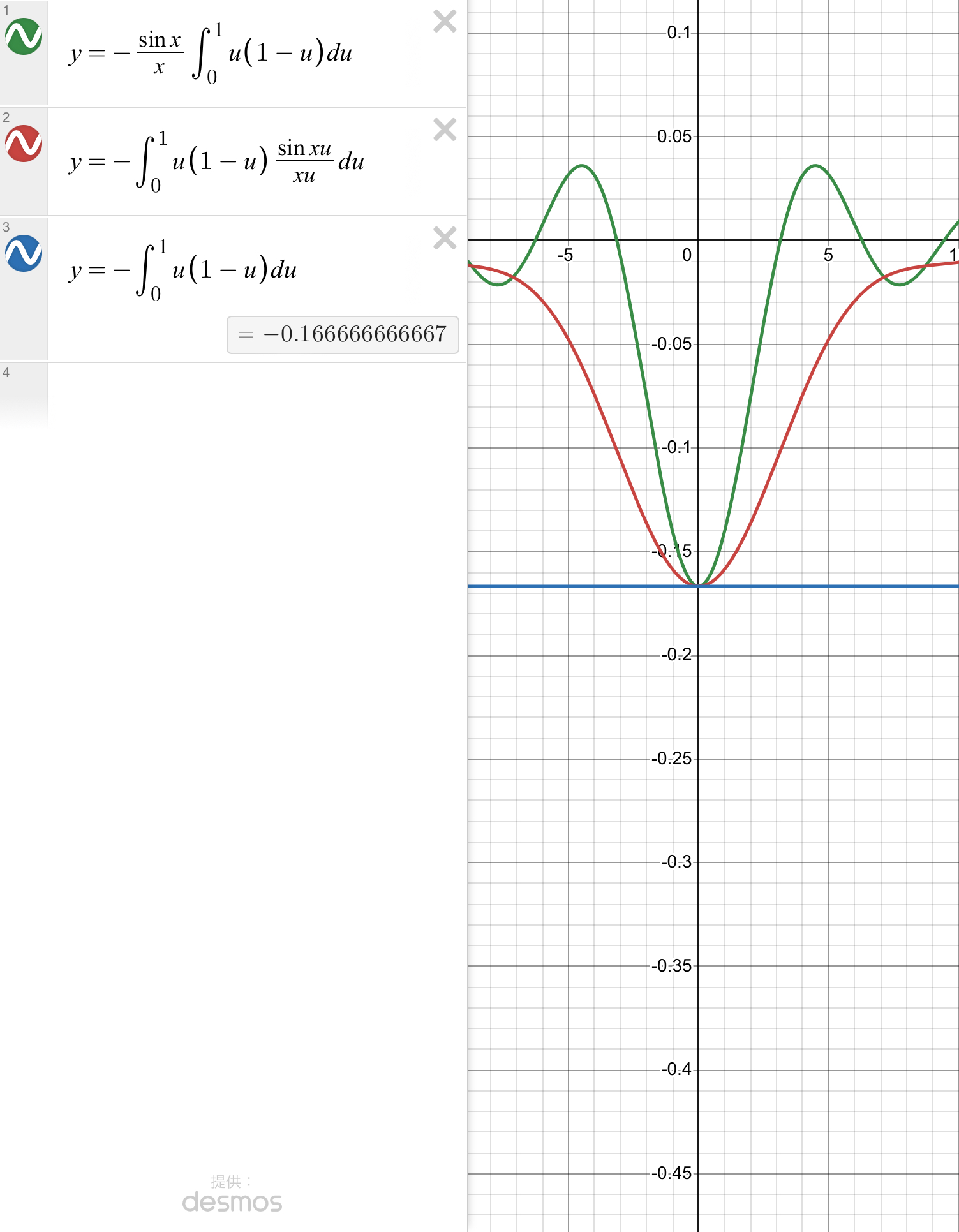Desmos様愛してます.
$$ \sin{x}-x=\int_{0}^{x}(\cos{t}-1)dt$$
でも解けるので書いておきます.この等式の証明は省略させていただきます.
以下が解法です.
$$\sin{x}-x=\int_{0}^{x}(\cos{t}-1)dt$$
$$=-2\int_{0}^{x}\sin^2{\dfrac{t}{2}}dt$$
$t=xu$とすると,解法1と同様に,
$$-2\int_{0}^{1}\sin^2{\dfrac{xu}{2}} \,xdu$$
であるから,
$$\dfrac{\sin{x}-x}{x^3}=-2\int_{0}^{1}\dfrac{\sin^2{\dfrac{xu}{2}}}{x^2}du=-\dfrac{1}{2}\int_{0}^{1}\dfrac{\sin^2{\dfrac{xu}{2}}}{\dfrac{x^2}{4}}du$$
$$=-\dfrac{1}{2}\int_{0}^{1}\Biggl(\dfrac{\sin{\frac{xu}{2}}}{\frac{x}{2}}\Biggl)^2du=-\dfrac{1}{2}\int_{0}^{1}u^2\Biggl(\dfrac{\sin{\frac{xu}{2}}}{\frac{xu}{2}}\Biggl)^2du$$
となる.積分区間で
$$\dfrac{\sin{\frac{x}{2}}}{\frac{x}{2}}\leqq\dfrac{\sin{\frac{xu}{2}}}{\frac{xu}{2}}\leqq 1$$
であるから,
$$-\dfrac{1}{2}\int_{0}^{1}u^2du\leqq-\dfrac{1}{2}\int_{0}^{1}u^2\Biggl(\dfrac{\sin{\frac{xu}{2}}}{\frac{xu}{2}}\Biggl)^2du\leqq-\dfrac{1}{2}\Biggl(\dfrac{\sin{\frac{x}{2}}}{\frac{x}{2}}\Biggl)^2\int_{0}^{1}u^2du$$
$x\to0$で,
$$\lim_{x\to0}\dfrac{\sin{x}-x}{x^3}=-\dfrac{1}{2}\int_{0}^{1}u^2du=-\dfrac{1}{6}$$
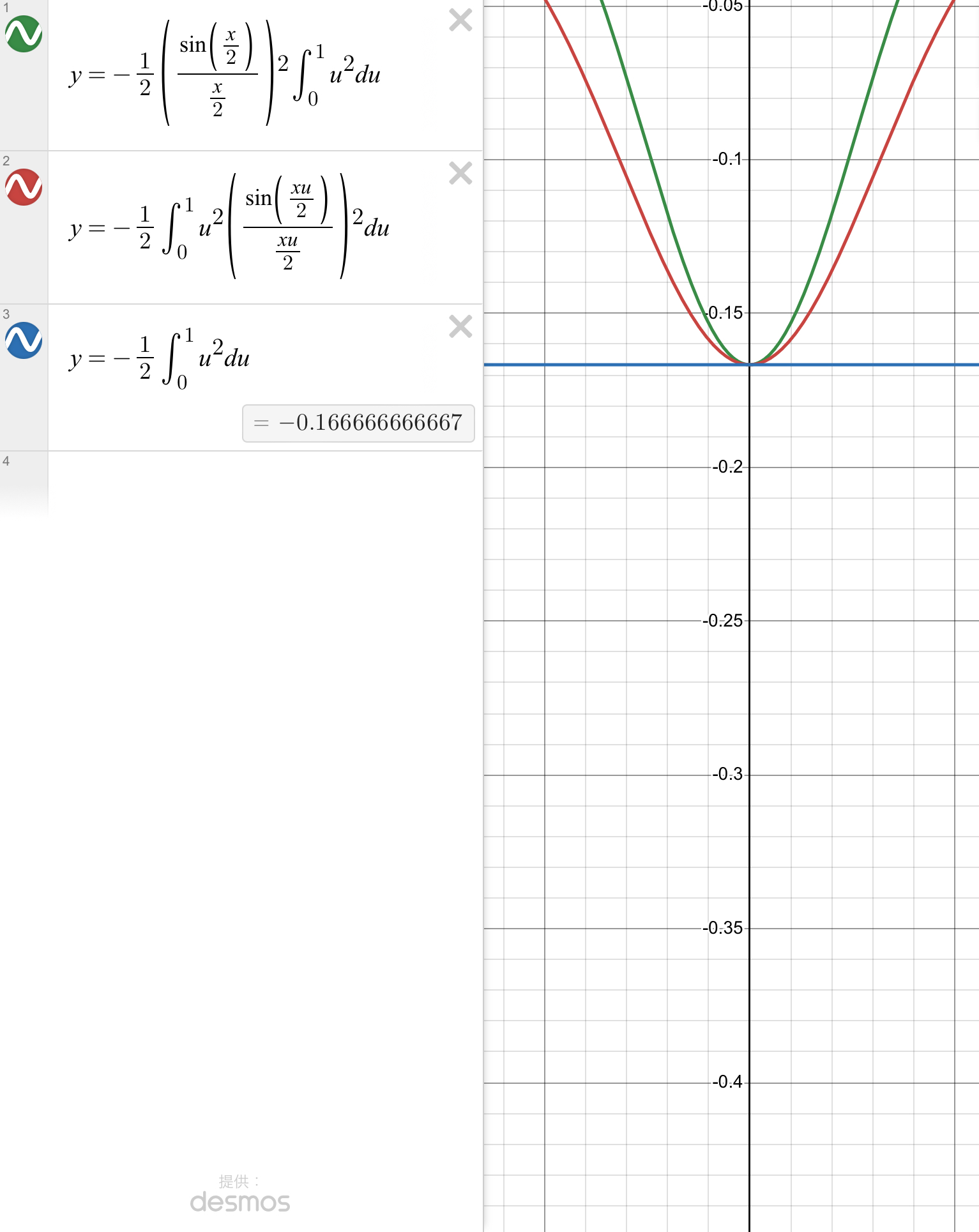Desmos様愛してますPart 2
どうしてもこういう系の極限が求められない場合ロピタルの定理使うより点数もらえそう!!!(???)
最後に
見つけたときとりあえず
めっちゃ嬉しかったので共有がしたかったです!!!!!!
ロピタルの定理
三角関数の多項式挟み
無しで解けたら教えてください(懇願)
この解法いろんな人に見せたい...笑
ではまた！！！
追記(投稿日同日)
$$ \sin{x}-x=\int_{0}^{x}(\cos{t}-1)dt$$
でもできます.
追加しておきました.
