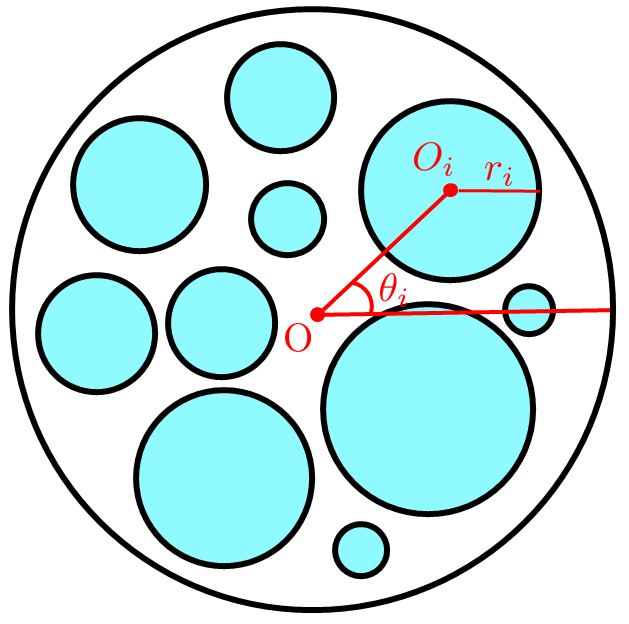
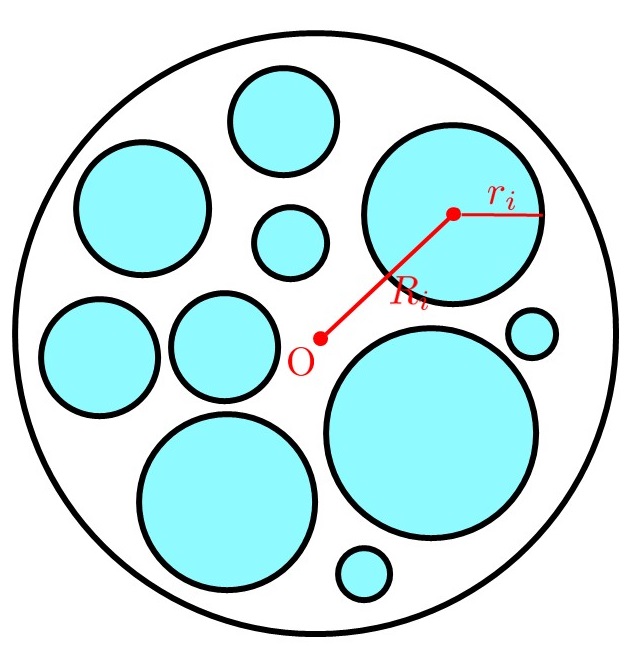
円の中に円をパッキングする際の必要条件
'Circle packing in a circle' という円の中に円をどれくらい詰め込められるかという問題があります.
この問題に関連して,円版内のいくつかの円版に関する以下の必要条件を導いたのでご紹介します.
半径$1$,中心$O$の円板内にいくつかの円板を被らないように配置する.
このとき,$i$番目の円板の半径を$r_i$, 中心から$O$までの距離を$R_i$としたとき,
$$ \displaystyle \sum_i (r_i \cdot R_i)^2 < \frac{1}{2}$$ が成り立つ.
$ $
この命題は,偏微分方程式論の以下の定理を用いて導きます.
開集合$\Omega \subset \mathbb{R}^N$に対して,$u \in C^2(\Omega)$は劣調和 ($i.e. -\Delta u \leq 0 ~~\mathrm{in}~~\Omega$)であり,$B\subset \Omega$を,中心$z \in \Omega$の$N$-次元球としたとき,以下の不等式が成立する.
$$ \displaystyle \frac{1}{|B|}\int_{B} u(x) ~dx\geq u(z).$$
ただし,$|B|$は$B$の$N$-次元ルベーグ測度.
この定理の証明は,例えば こちら のノートを参照してください.
それでは,この平均値の性質を認めた上で,最初に紹介した命題を証明しましょう.
$B_r(x,y)$を半径$r$,中心$(x,y)$の円板とする.円板族$\displaystyle \left\{B_{r_i}(x_i,y_i)\right\}_{i}$を,
$\displaystyle B_1(0,0) \supset \bigcup_{i} B_{r_i}(x_i,y_i)$かつ, $i \neq j \Rightarrow B_{r_i}(x_i,y_i) \cap B_{r_j}(x_j,y_j) = \emptyset$
を満たすものとする.
ここで,$u(x,y) = x^2 + y^2$とおくと,$u$は正値より,
\begin{align*}
\int_{B_1(0,0)} u(x,y) ~dxdy &\geq \int_{\bigcup_{i} B_{r_i}(x_i,y_i)} u(x,y)~dxdy \\
&= \sum_{i} \int_{B_{r_i}(x_i,y_i)} u(x,y)~dxdy.
\end{align*}
また,$-\Delta u \equiv -4 < 0$より,$u$は劣調和関数である.よって平均値の性質から,
\begin{align*}
\sum_{i} \int_{B_{r_i}(x_i,y_i)} u(x,y)~dxdy &> \sum_{i}|B_{r_i}(x_i,y_i)| ~u(x_i,y_i) \\
&= \pi \sum_{i} r_i^2 ~(x_i^2 + y_i^2).
\end{align*}
また,$\displaystyle \int_{B_1(0,0)} u(x,y) ~dxdy$について,$x = r \cos \theta$, $y = r\sin \theta$とおけば,
\begin{align*}
\int_{B_1(0,0)} u(x,y) ~dxdy &= \int_0^{2\pi} \int_0^1 r^2 \cdot rdr d\theta \\
&= 2\pi \int_0^1 r^3 ~dr\\
&=\frac{\pi}{2}.
\end{align*}
したがって,
$ \displaystyle \pi \sum_{i} r_i^2 (x_i^2 + y_i^2) < \frac{\pi}{2} \Leftrightarrow \sum_{i} (r_i \cdot R_i)^2 < \frac{1}{2}$
となる.
今回の方法は,劣調和関数として$u(x,y) = x^2 + y^2$を選びましたが,他の正値な劣調和関数を使えば,円のパッキングに関する様々な不等式を得ることができます.
例えば,$2$次元のラプラシアンは,極座標表示で
$\displaystyle \Delta = \frac{1}{r} \frac{\partial}{\partial r} + \frac{\partial^2}{\partial r^2} + \frac{1}{r^2} \frac{\partial^2}{\partial \theta^2}$となることに注意すれば,以下のような命題も上と同様に示すことが出来ます.
$xy$-平面上の半径$1$,中心$O ~(0,0)$の円板内にいくつかの円板を被らないように配置する.
このとき,$i$番目の円板の半径を$r_i$, 中心を$O_i$として,$O O_i$と$x$軸がなす角を$\theta_i$とする.
さらに,$f \in C^2(0,2\pi)$を正値凸関数としたとき,
$$\displaystyle \sum_{i} r_i^2 f(\theta_i) \leq \frac{1}{2\pi}\int_0^{2\pi} f(\theta) ~d\theta$$
が成り立つ.