院解5 京大数学系H29 基礎6 位相　tube lemmaの一部

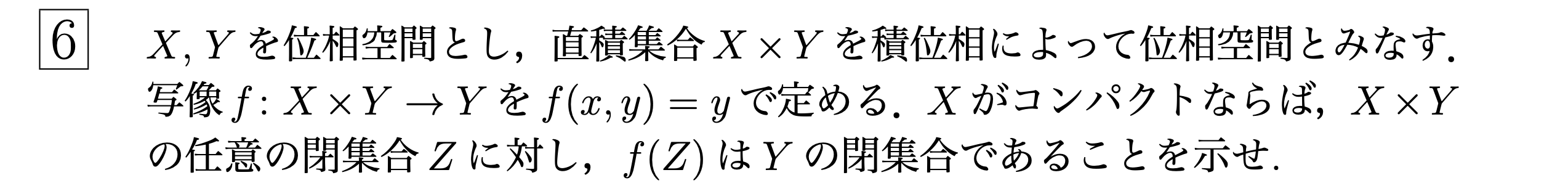
$Y\backslash f(Z)$が開集合であることをみる.$y\in Y\backslash f(Z)$とする.任意の$x\in X$に対し,$X,\ Y$のある開集合$U_x,\ V_x$が存在して
$(x,y)\in U_x\times V_x\subseteq X\times Y\backslash Z$を満たす.$\{U_x\}_{x\in X}$は$X$の開被覆だから$X$のコンパクト性から有限部分被覆を取り出すことができる.有限部分被覆を$U_{x_1},U_{x_2},...,U_{x_n}$とする.$\tilde{V_y}=\displaystyle \bigcap_i V_{x_i}$とおく.任意に$x\in X$をとると,被覆だからある$i$に対し$x\in U_{x_i}$となる.この$i$に対し
$(x,y)\in U_{x_i}\times \tilde{V_y}\subseteq U_{x_i}\times V_{x_i}\subseteq X\times Y\backslash Z$.$x\in X$は任意だったから$X\times \tilde{V_y}\subseteq X\times Y\backslash Z$.
$f(\displaystyle\bigcup_{y\in Y} X\times \tilde{V_y})=X\times Y\backslash Z$で$f$は開写像だから開.$\Box$