平面上の二色の点群と、同じ色の点のみを通る直線の存在について
本記事では1970年にG. D. Chakerian GDCにより示された二色に塗り分けられた平面上の点群に関する以下の定理をご紹介します.
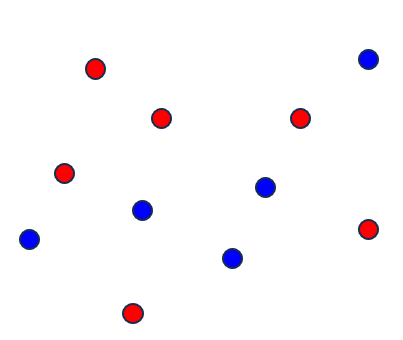
$2$次元平面上に有限個の点があり, 赤か青の色が付いている.
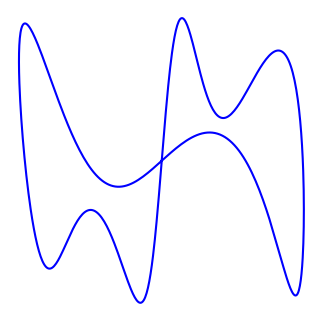
ただし, 以下の図のように一直線上に全ての点が並んでいないものとする.

このとき, 2点以上の同じ色の点だけを通る直線を引くことが出来る.
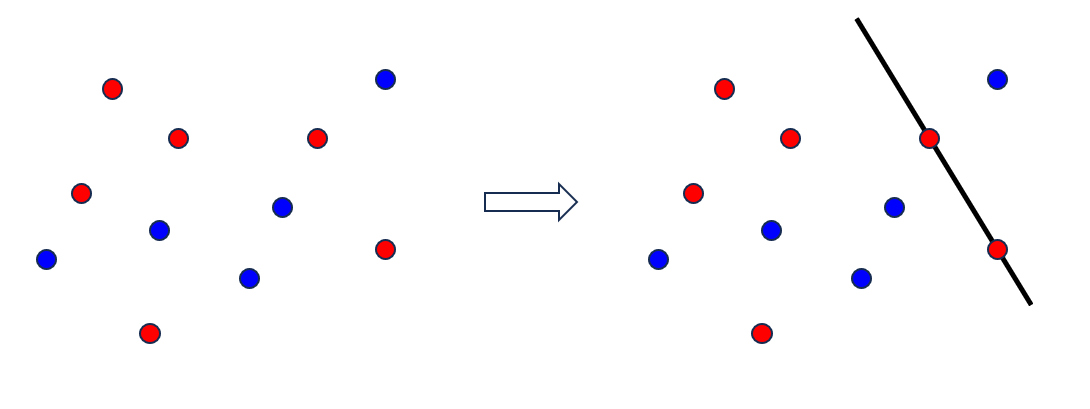
とてもシンプルな定理ですが, 自明ではありません. また点の数を増やせば, 同じ色の点だけを通る直線の候補が大きく変わり得るため, 帰納法をうまく使うことは出来ません. しかし以下の方針でとても鮮やかに証明することができます.
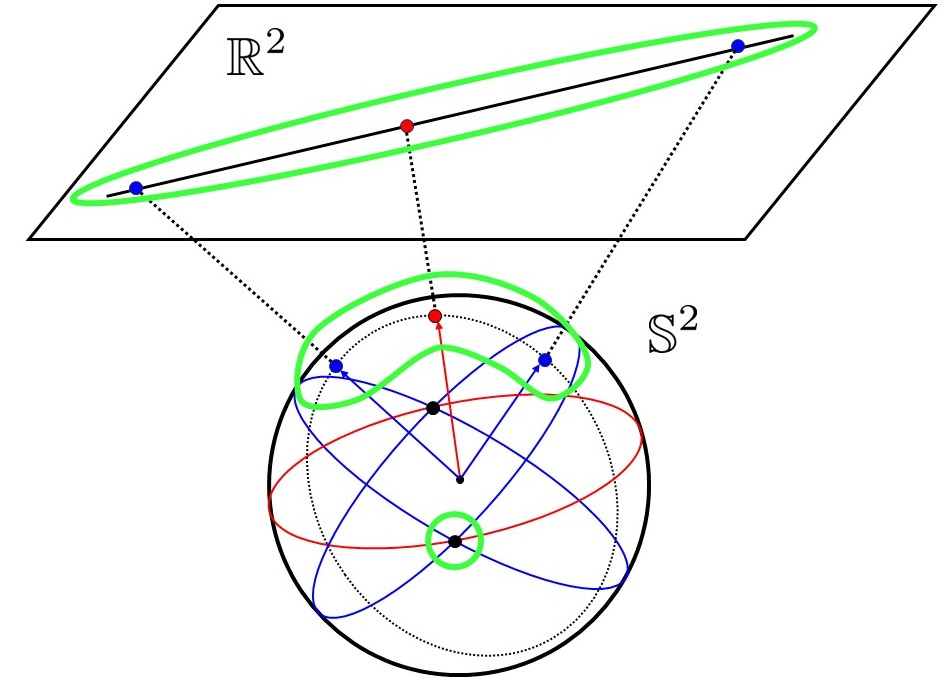
まず以下のように, $2$次元平面上の点群を$2$次元球面に射影します.
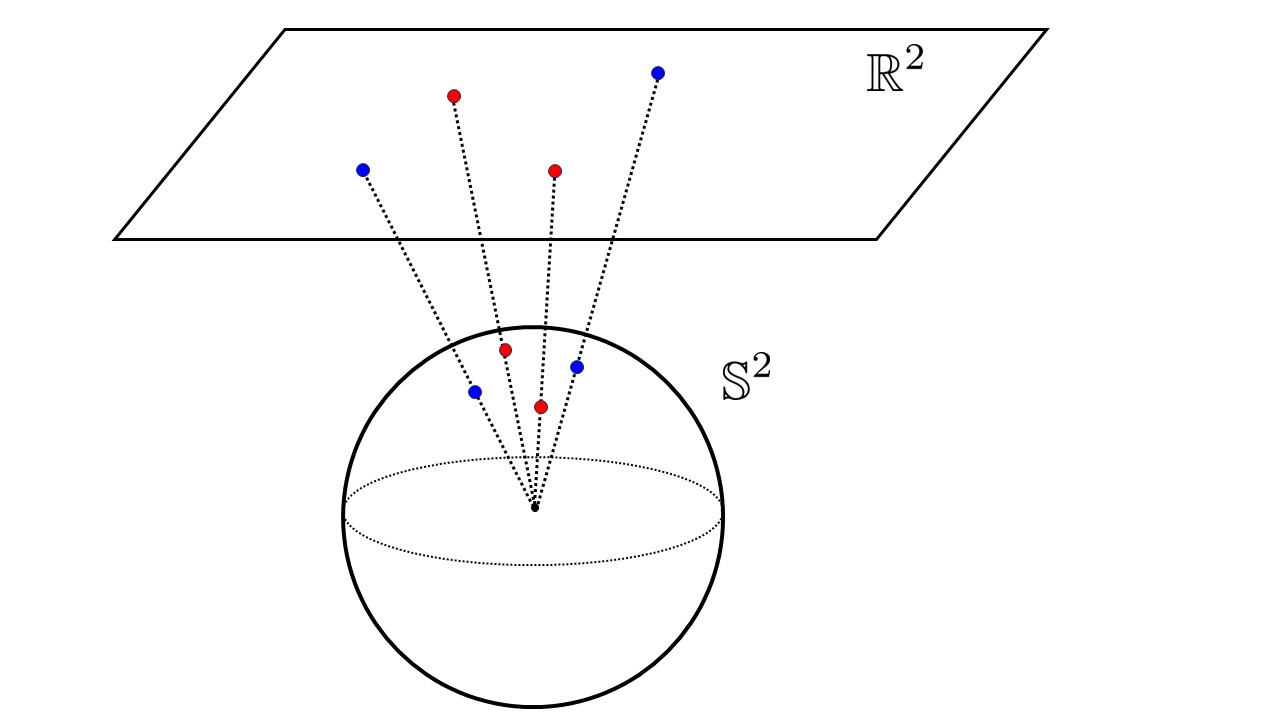 平面上の点の球面への射影
平面上の点の球面への射影
さらに, $\mathbb{S}^2$を$\mathbb{R}^3$上の原点を中心に持つ$2$次元球面と思い, 以下の図のように, $2$次元球面上の点$p \in \mathbb{S}^2 \subset \mathbb{R}^3$(および$p$の対蹠点$-p$との組)から, 大円(球の中心を通る平面と球面との交線)$C$を, $C = \{q \in \mathbb{S}^2 \mid \langle p,q \rangle = 0\} $として$1:1$対応させます.
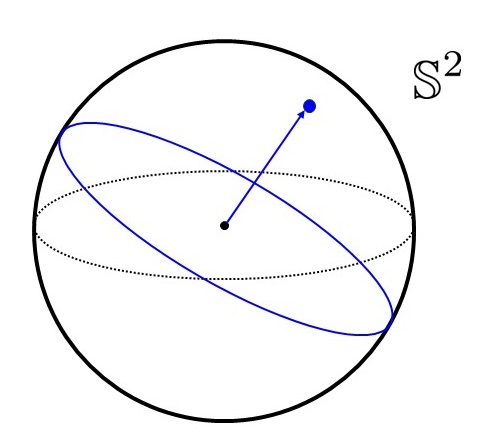 球面上の点と大円の対応
球面上の点と大円の対応
ここで, 「平面上の点群が同一直線上にある」$\Leftrightarrow$「球面へ射影した点群が同一大円上にある」$\Leftrightarrow$「それぞれの点に対応する大円が共通の交点を持っている」ということに注意します.
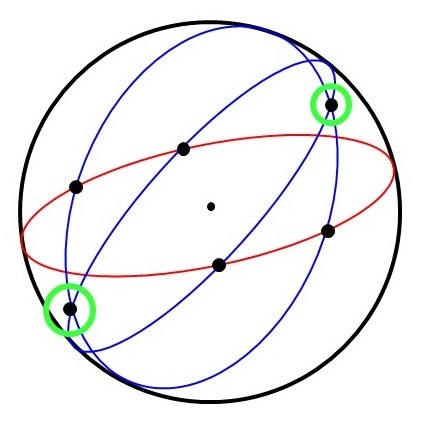
したがって, 元々の主張は次の球面$\mathbb{S}^2$上のグラフの主張に帰着されます. ('一直線上に全ての点が並んでいない'という条件から単純グラフで考えれば十分であることに注意してください. )
$\mathbb{S}^2$上に$3$つ以上の赤か青の大円があり, 大円どうしの交点を'頂点'として, さらに頂点と頂点を結ぶ大円の弧を'辺'としたグラフが単純グラフであるとき, 必ず同じ色の辺のみを接合する頂点を持つ.
ここで, グラフの記号を整理します. グラフ$G$の頂点からなる集合を$V$, 辺からなる集合を$E$, 面からなる集合を$F$として, それぞれの個数を$\#V, \#E , \#F$で表します. また, $k$個の辺からなる面の個数を$f_k$と表します.
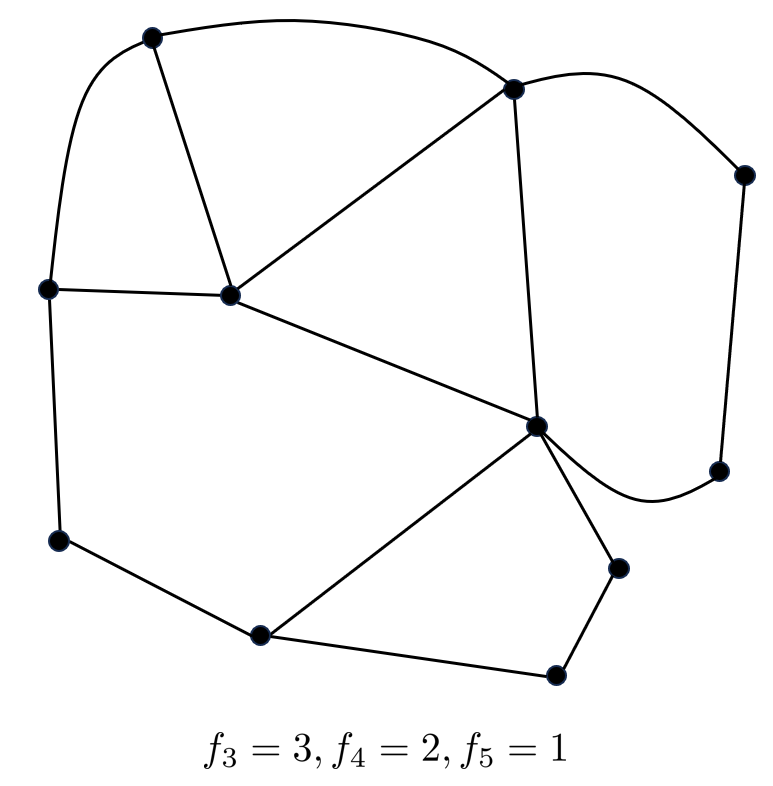 グラフの例
グラフの例
$\#V \geq 3$となる単純グラフには$2$個以下の辺からなる面は存在しないことから, 以下が成り立つことに注意します.
\begin{align}
\# F &= f_3 + f_4 + f_5 + \ldots, \\
2 \cdot \# E &= 3 f_3 + 4 f_4 + 5 f_5 + \ldots
\end{align}
ここで, 異なる色の辺に挟まれた角のことを'異色角'と呼ぶことにしましょう. さらに, $v \in V$に対して, $c(v)$を$v$を頂点として持つような異色角の個数とします. 例えば以下の図のような頂点の場合, $c(v)=4$となります.
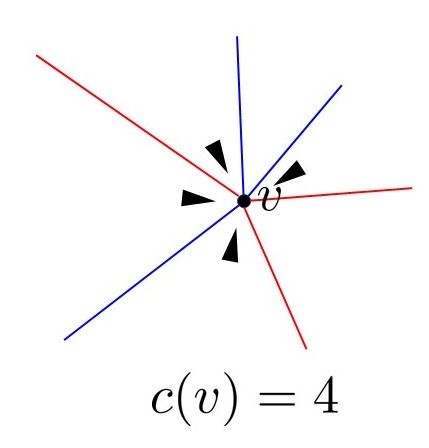
この準備のもとで, 背理法により定理の言い換えを証明しましょう.
全ての大円どうしの交点において,必ず異なる色の大円と交わっていると仮定します. すると, 各頂点$v \in V$に対して, $4 \leq c(v)$が成立します. したがって,異色角の個数のトータルを考えると,
\begin{equation}
4 \cdot \#V \leq \sum_{v \in V} c(v) \quad \ldots (1)
\end{equation}
となります. また, $k$個の辺からなる面において, 異色角となる内角の個数は, $k$が奇数ならば$k-1$個, $k$が偶数ならば $k$個が最大となります.
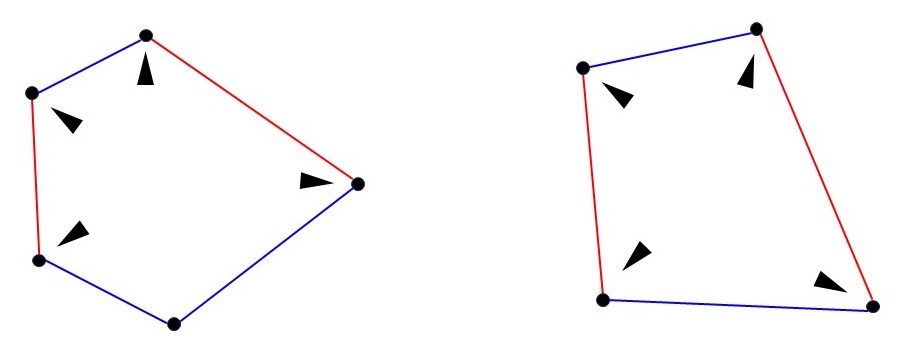
よって,
\begin{equation}
\sum_{v \in V} c(v) \leq 2 f_3 + 4 f_4 + 4 f_5 + 6 f_6 + 6 f_7 + \ldots \quad \ldots (2)
\end{equation}
となります. また,
\begin{align}
& 2 f_3 + 4 f_4 + 4 f_5 + 6 f_6 + 6 f_7 +\ldots \\
&\leq 2 f_3 + 4 f_4 + 6 f_5 + 8 f_6 + 10 f_7 + \ldots \\
&= 2(3 f_3 + 4 f_4 + 5 f_5 + \ldots) - 4(f_3 + f_4 + f_5 + \ldots) \\
&= 4\cdot\#E - 4\cdot\#F \quad \ldots (3)
\end{align}
より, $(1),(2),(3)$をまとめると, $\#V - \#E + \#F \leq 0$となります. これはオイラーの多面体定理$\#V - \#E + \#F = 2$と矛盾します.