【雑記】熱核と "Heat Ball"
0. Intro.
この記事は雑記（兼忘備録）の形式を採っているので，意図的に未完成の部分があります。
徐々に出来上がっていきますが，全体的な完成の形はありません。
${}$
1. 熱核と "Heat Ball"
以下では，$N \in \mathbb{N}$ とする。
関数 $\Psi \, : \, \mathbb{R}^{N} \times (0 , \infty) \to \mathbb{R}$ を，
\begin{align}
\qquad
\begin{aligned}
\Psi (x ,\, t)
:=
\left( 4 \pi t \right)^{- \frac{N}{2}} e^{- \frac{|x|^{2}}{4t}}
\qquad
\left(
\
\forall \, (x ,\, t) \in \mathbb{R}^{N} \times ( 0 ,\, \infty )
\
\right)
\end{aligned}
\end{align}
と定める。この $\Psi$ を，$N$ 次元 熱核 や ガウス核 等と呼ぶ。
熱核の性質
- $\Psi \in C^{\infty} \left( \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \right)$ である。
- $\Psi$ は空間変数について既に 正規化 された状態で定義されている。すなわち，
\begin{align} \qquad \begin{aligned} \forall \, t > 0 \, \boldsymbol{,} \quad \int_{\mathbb{R}^{N}} \Psi \left( x ,\, t \right) \, dx = 1 \end{aligned} \end{align}
となるように定義されている。実際に，任意の $t > 0$ と各 $j \in \left\{ 1 ,\, \dots ,\, N \right\}$ に対して，
\begin{align} \qquad \begin{aligned} \int_{-\infty}^{\infty} e^{- \dfrac{x_{j}^{2}}{4t}} \, dx_{j} &= \left\{ \left( \int_{-\infty}^{\infty} e^{ -\dfrac{x_{j}^{2}}{4t} } \, dx_{j} \right) \left( \int_{-\infty}^{\infty} e^{ -\dfrac{y_{j}^{2}}{4t} } \, dy_{j} \right) \right\}^{\dfrac{1}{2}} \\[5pt] &= \left( \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{ -\dfrac{x_{j}^{2} + y_{j}^{2}}{4t} } \, dx_{j} \, dy_{j} \right)^{\dfrac{1}{2}} \\[5pt] &= \left( 4t \int_{0}^{2 \pi} \, d \theta \int_{0}^{\infty} r e^{-r^{2}} \, dr \right)^{\dfrac{1}{2}} \\[5pt] &= \left( 4t \cdot 2 \pi \left[ -\frac{1}{2} e^{-r^{2}} \right]_{0}^{\infty} \right)^{\dfrac{1}{2}} \\[5pt] &= \left( 4 \pi t \right)^{\dfrac{1}{2}} \end{aligned} \end{align}
であることから，
\begin{align} \qquad \begin{aligned} \int_{\mathbb{R}^{N}} \Psi \left( x ,\, t \right) \, dx &= \left( 4 \pi t \right)^{-\tfrac{N}{2}} \int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} e^{- \tfrac{x_{1}^{2} + \dots + x_{N}^{2}}{4t}} \, dx_{1} \cdots dx_{N} \\[5pt] &= \left( 4 \pi t \right)^{-\dfrac{N}{2}} \prod_{j=1}^{N} \int_{-\infty}^{\infty} e^{-\dfrac{x_{j}^{2}}{4t}} \, dx_{j} \\[5pt] &= \left( 4 \pi t \right)^{-\dfrac{N}{2}} \cdot \left( 4 \pi t \right)^{\dfrac{N}{2}} \\[5pt] &= 1 \, \boldsymbol{.} \end{aligned} \end{align} - 任意の $\left( x ,\, t \right) \in \mathbb{R}^{N} \times \left( 0 ,\, \infty \right)$ に対して，
\begin{align} \qquad \begin{aligned} \dfrac{\partial \Psi}{\partial t} \left( x ,\, t \right) - \Delta \Psi \left( x ,\, t \right) = 0 \end{aligned} \end{align}
となる。
${}$
$\left(x , \, t \right) \in \mathbb{R}^{N} \times \mathbb{R} \, \boldsymbol{,} \ \ r > 0$ とする。このとき，部分集合 $E \left( x , \, t \, ; \, r \right) \subset \mathbb{R}^{N} \times \mathbb{R}$ を，
\begin{align}
\qquad
\begin{aligned}
E \left( x ,\, t \, ; \, r \right)
:=
\left\{
\,
\left( y ,\, s \right) \in \mathbb{R}^{N} \times \mathbb{R}
\ \ \middle\vert \ \
s < t
\quad \textsf{かつ} \quad
\Psi \left( x - y ,\, t - s \right) \geq \dfrac{1}{r^{N}}
\,
\right\}
\end{aligned}
\end{align}
と定める。これを "Heat Ball" と呼ぶ。
${}$
"Heat Ball" の概形
$\displaystyle
\Psi \left( x ,\, t \right)
=
\left( 4 \pi t \right)^{- \frac{N}{2}} e^{- \frac{|x|^{2}}{4t}}
$ より，$s < t$ の場合は，
\begin{align}
\qquad
\begin{aligned}
\Psi \left( x - y ,\, t - s \right) \geq \dfrac{1}{r^{N}}
\qquad \Longleftrightarrow \qquad
0
\leq
\left| x - y \right|^{2}
\leq
2N \left( t - s \right) \log \left( \dfrac{r^{2}}{ 4 \pi \left( t - s \right) } \right)
\end{aligned}
\end{align}
であるので，
\begin{align}
\qquad
\begin{aligned}
\log \left( \dfrac{r^{2}}{ 4 \pi \left( t - s \right) } \right)
\geq
0 \, \boldsymbol{,}
\qquad \textsf{すなわち，} \qquad
\dfrac{r^{2}}{ 4 \pi \left( t - s \right) } \geq 1 \, \boldsymbol{.}
\end{aligned}
\end{align}
ゆえに，$t - s \leq \dfrac{r^{2}}{4 \pi}$ かつ $s < t$ より，
\begin{align}
\qquad
\begin{aligned}
t - \dfrac{r^{2}}{4 \pi} \leq s < t \, \boldsymbol{.}
\end{aligned}
\end{align}
このことから，
\begin{align}
\qquad
\begin{aligned}
E \left( x ,\, t \, ; \, r \right)
&=
\left\{
\,
\left( y ,\, s \right) \in \mathbb{R}^{N} \times \mathbb{R}
\ \ \middle\vert \ \
s < t
\quad \textsf{かつ} \quad
\Psi \left( x - y ,\, t - s \right) \geq \dfrac{1}{r^{N}}
\,
\right\}
\\[5pt]
&=
\left\{
\,
\left( y ,\, s \right) \in \mathbb{R}^{N} \times \mathbb{R}
\ \ \middle\vert \ \
t - \dfrac{r^{2}}{4 \pi} \leq s < t
\quad \textsf{かつ} \quad
\left| x - y \right|^{2}
\leq
2N \left( t - s \right)
\left\{ \log r^{2} - \log \left( 4 \pi \left( t - s \right) \right) \right\}
\,
\right\}
\end{aligned}
\end{align}
となるので，
\begin{align}
\qquad
\begin{aligned}
E \left( \boldsymbol{0} ,\, 0 \, ; \, r \right)
=
\left\{
\,
\left( y ,\, s \right) \in \mathbb{R}^{N} \times \mathbb{R}
\ \ \middle\vert \ \
- \dfrac{r^{2}}{4 \pi} \leq s < 0
\quad \textsf{かつ} \quad
\left| y \right|
\leq
\sqrt{
2N \left( - s \right)
\left\{ \log r^{2} - \log \left( - 4 \pi s \right) \right\}
}
\,
\right\}
\, \boldsymbol{.}
\end{aligned}
\end{align}
ここで，
\begin{align}
\qquad
\begin{aligned}
k \left( s \right)
:=
\sqrt{ 2N \left( - s \right) \left\{ \log r^{2} - \log \left( - 4 \pi s \right) \right\} }
\qquad
\left( \, - \dfrac{r^{2}}{4 \pi} \leq s < 0 \, \right)
\end{aligned}
\end{align}
とすると，
\begin{align}
\qquad
\begin{aligned}
\forall \, s \in \left( -\dfrac{r^{2}}{4 \pi} ,\, 0 \right) \, \boldsymbol{,}
\qquad
k \left( s \right) > 0
\end{aligned}
\end{align}
であるので，
\begin{align}
\qquad
\begin{aligned}
k' \left( s \right)
=
\dfrac{1}{ 2 k \left( s \right) }
\cdot
\dfrac{d}{ds} \left[ \left\{ k \left( s \right) \right\}^{2} \right]
=
\dfrac{N}{ k \left( s \right) }
\left\{ - \log r^{2} + \log \left( - 4 \pi s \right) + 1 \right\}
\, \boldsymbol{.}
\end{aligned}
\end{align}
ゆえに，
\begin{align}
\qquad
\begin{aligned}
\left[
\
k' \left( s \right) = 0
\quad \textsf{かつ} \quad
- \dfrac{r^{2}}{4 \pi} < s < 0
\
\right]
\qquad \Longleftrightarrow \qquad
s = - \dfrac{r^{2}}{4 \pi e}
\end{aligned}
\end{align}
となることから，$k$ の極大値は，
\begin{align}
\qquad
\begin{aligned}
k \left( - \dfrac{r^{2}}{4 \pi e} \right)
=
r \sqrt{\dfrac{N}{2 \pi e}}
\ \boldsymbol{.}
\end{aligned}
\end{align}
さらに，
\begin{align}
\qquad
\begin{aligned}
&
k \left( - \frac{r^{2}}{4 \pi} \right) = 0 \, \boldsymbol{,}
\qquad
\lim_{s \to -0} k \left( s \right) = 0 \ \boldsymbol{;}
\\[10pt]
&
\lim_{s \to - \frac{r^{2}}{4 \pi} + 0} k' \left( s \right) = + \infty \, \boldsymbol{,}
\qquad
\lim_{s \to -0} k' \left( s \right) = - \infty
\, \boldsymbol{.}
\end{aligned}
\end{align}
${}$
よって，$E \left( \boldsymbol{0} ,\, 0 \, ; \, r \right)$ および $\partial E \left( \boldsymbol{0} ,\, 0 \, ; \, r \right)$ を，例えば，
\begin{align}
\qquad
\begin{aligned}
N = 1 \, \boldsymbol{,}
\quad
r = \sqrt{4 \pi} \, \boldsymbol{,}
\quad
-1 \leq s \leq 0 \, \boldsymbol{,}
\quad
- k \left( s \right) \leq y \leq k \left( s \right)
\end{aligned}
\end{align}
として 平面的に 図示すると，下図のようになる：
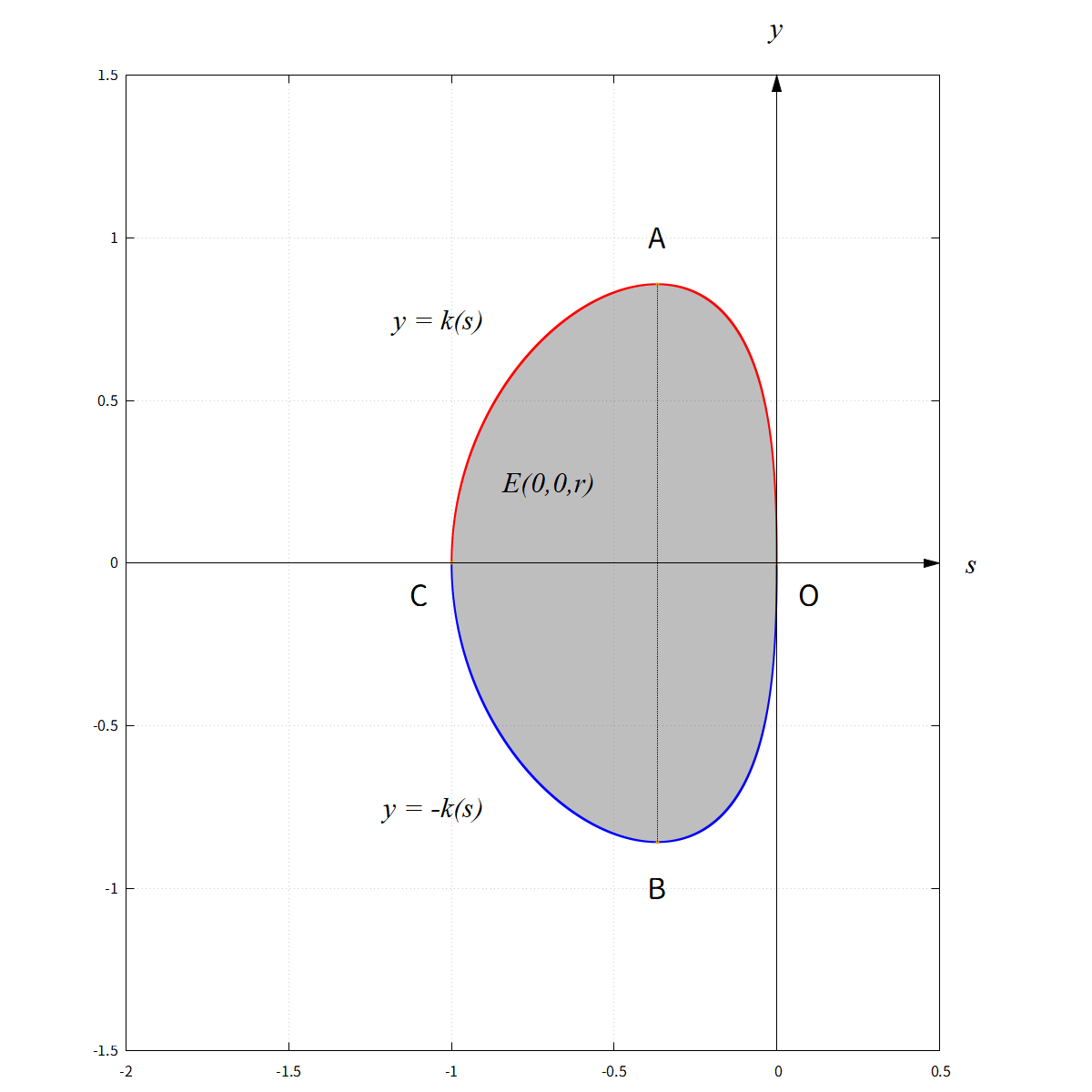"Heat Ball" とその境界の概形
ここで，
\begin{align}
\qquad
\begin{aligned}
\partial E \left( \boldsymbol{0} ,\, 0 \, ; \, r \right)
=
\left\{
\,
\left( y ,\, s \right) \in \mathbb{R}^{N} \times \mathbb{R}
\ \ \middle\vert \ \
-\frac{r^{2}}{4 \pi} \leq s < 0
\quad \textsf{かつ} \quad
\left| y \right| = k \left( s \right)
\,
\right\}
\cup
\biggl\{ \, \left( \boldsymbol{0} ,\, 0 \right) \, \biggr\}
\end{aligned}
\end{align}
である。
${}$
2. "Heat Ball" 上の積分
\begin{align} \qquad \begin{aligned} \iint_{E \left( \boldsymbol{0} ,\, 0 \,;\, 1 \right)} \dfrac{\left| y \right|^{2}}{s^{2}} \, dy \, ds = 4 \, \boldsymbol{.} \end{aligned} \end{align}
以下では，
\begin{align}
\qquad
\begin{aligned}
\Gamma \left( m \right) := \int_{0}^{\infty} t^{m-1} e^{-t} \, dt
\quad
\left( \ \forall \, m > 0 \ \right)
\, \boldsymbol{,}
\qquad
\varpi_{N}
:=
\int_{\left| y \right| \leq 1} 1 \, dy
=
\dfrac{\pi^{\frac{N}{2}}}{ \Gamma \left( \frac{N}{2} + 1 \right) }
\end{aligned}
\end{align}
とする。
${}$
積分を直接計算することにより，
\begin{align}
\qquad
\begin{aligned}
\iint_{E \left( \boldsymbol{0} ,\, 0 \,;\, 1 \right)}
\dfrac{\left| y \right|^{2}}{s^{2}}
\, dy \, ds
&=
\int_{- \frac{1}{4 \pi}}^{0}
\dfrac{1}{s^{2}}
\left(
\int_{ \left| y \right|^{2} \leq 2Ns \log \left( - 4 \pi s \right) }
\left| y \right|^{2}
\, dy
\right)
\, ds
\\[5pt]
&=
\int_{- \frac{1}{4 \pi}}^{0}
\dfrac{1}{s^{2}}
\left\{
\int_{0}^{\sqrt{2Ns \log \left( - 4 \pi s \right)}} dr
\int_{\left| y \right| = r} \left| y \right|^{2} \, dS \left( y \right)
\right\}
\, ds
\\[5pt]
&=
\int_{- \frac{1}{4 \pi}}^{0}
\dfrac{1}{s^{2}}
\left(
\int_{0}^{\sqrt{2Ns \log \left( - 4 \pi s \right)}}
N \varpi_{N} r^{N-1+2}
\, dr
\right)
\, ds
\\[5pt]
&=
\dfrac{N \varpi_{N}}{N+2}
\int_{- \frac{1}{4 \pi}}^{0}
\dfrac{1}{\left( -s \right)^{2}}
\left\{ -2N \left( -s \right) \log \left( 4 \pi \left( -s \right) \right) \right\}^{\frac{N+2}{2}}
\, ds
\\[5pt]
&=
\dfrac{N \varpi_{N} \left( 2N \right)^{\frac{N+2}{2}}}{N+2}
\int_{- \frac{1}{4 \pi}}^{0}
\left( -s \right)^{\frac{N-2}{2}}
\left\{ - \log \left( 4 \pi \left( -s \right) \right) \right\}^{\frac{N+2}{2}}
\, ds
\\[5pt]
&=
\dfrac{N \varpi_{N} \left( 2N \right)^{\frac{N+2}{2}}}{N+2}
\int_{0}^{\infty}
\left( \dfrac{e^{- \tau}}{4 \pi} \right)^{\frac{N}{2}}
\tau^{\frac{N+2}{2}}
\, d\tau
\\[5pt]
&=
\dfrac{N \varpi_{N} \left( 2N \right)^{\frac{N+2}{2}}}{N+2}
\cdot
\left( 4 \pi \right)^{- \frac{N}{2}}
\int_{0}^{\infty} \tau^{\frac{N+2}{2}} e^{- \frac{N}{2} \tau} \, d\tau
\\[5pt]
&=
\dfrac{N \varpi_{N} \left( 2N \right)^{\frac{N+2}{2}}}{N+2}
\cdot
\left( 4 \pi \right)^{- \frac{N}{2}}
\int_{0}^{\infty}
\left( \dfrac{2}{N} \right)^{\frac{N+4}{2}} p^{\frac{N+2}{2}} e^{-p}
\, dp
\\[5pt]
&=
\dfrac{8 \pi^{- \frac{N}{2}}}{N+2}
\cdot
\varpi_{N}
\cdot
\int_{0}^{\infty} p^{\frac{N+4}{2} - 1} e^{-p} \, dp
\\[5pt]
&=
\dfrac{8 \pi^{- \frac{N}{2}}}{N+2}
\cdot
\varpi_{N}
\cdot
\Gamma \left( \frac{N}{2} + 2 \right)
\\[5pt]
&=
\dfrac{8 \pi^{- \frac{N}{2}}}{N+2}
\cdot
\dfrac{\pi^{\dfrac{N}{2}}}{\Gamma \left( \frac{N}{2} + 1 \right)}
\cdot
\Gamma \left( \frac{N}{2} + 2 \right)
\\[5pt]
&=
\dfrac{8}{N+2}
\cdot
\left\{ \Gamma \left( \dfrac{N}{2} + 1 \right) \right\}^{-1}
\cdot
\left( \dfrac{N}{2} + 1 \right) \Gamma \left( \dfrac{N}{2} + 1 \right)
\\[5pt]
&=
\dfrac{8}{N+2} \cdot \dfrac{N+2}{2}
\\[5pt]
&=
4
\, \boldsymbol{.}
\end{aligned}
\end{align}
なお，証明では，$\Gamma$ 関数の性質と，公式
\begin{align}
\qquad
\begin{aligned}
\int_{B \left( x_{0} ,\, R \right)} f \left( y \right) \, dy
=
\int_{0}^{R} dr \int_{\partial B \left( x_{0} ,\, r \right)} f \left( y \right) \, dS(y)
\qquad
\left(
\
\begin{aligned}
&
x_{0} \in \mathbb{R}^{N} \boldsymbol{,} \ \
R > 0 \, \boldsymbol{,} \ \
f \in C^{0} \left( \overline{B \left( x_{0} ,\, R \right)} \right) \, \boldsymbol{,}
\\[5pt]
&
B \left( x_{0} ,\, R \right)
:=
\left\{
\
x \in \mathbb{R}^{N}
\ \middle\vert \
\left| x - x_{0} \right| < R
\
\right\}
\end{aligned}
\
\right)
\end{aligned}
\end{align}
を用いた。
${}$
3. 平均値定理
上記の補題を用いると，以下のことが証明できる。
$\Omega$ を $\mathbb{R}^{N}$ 内の空でない有界な開集合，$T > 0$ とし，
\begin{align}
\qquad
\begin{aligned}
\Omega_{T} := \Omega \times \left( 0 ,\, T \right]
\end{aligned}
\end{align}
とする。また，関数 $u \in C^{2 ,\, 1} \left( \Omega_{T} \right)$ を，熱方程式
\begin{align}
\qquad
\begin{aligned}
\dfrac{\partial u}{\partial t} \left( x ,\, t \right)
-
\Delta u \left( x ,\, t \right)
=
0
\qquad
\left( \ \forall \, ( x ,\, t ) \in \Omega_{T} \ \right)
\end{aligned}
\end{align}
の解とする。このとき，任意の
\begin{align}
\qquad
\begin{aligned}
\left( x ,\, t \, ; \, r \right)
\in
\left\{
\,
\left( x ,\, t \, ; \, r \right) \in \Omega_{T} \times \left( 0 ,\, \infty \right)
\ \ \middle\vert \ \ {\vphantom{\dfrac{0}{0}}}
E \left( x ,\, t \, ; \, r \right) \subset \Omega_{T}
\,
\right\}
\end{aligned}
\end{align}
に対して，
\begin{align}
\qquad
\begin{aligned}
u \left( x ,\, t \right)
=
\dfrac{1}{4 r^{N}}
\iint_{E \left( x ,\, t \, ; \, r \right)}
u \left( y ,\, s \right)
\dfrac{\left| x - y \right|^{2}}{\left( t - s \right)^{2}}
\, dy \, ds
\end{aligned}
\end{align}
が成り立つ。
- $\Omega_{T}$ を Parabolic Cylinder と呼ぶ。
- また，
\begin{align} \qquad \begin{aligned} C^{2 ,\, 1} \left( \Omega_{T} \right) := \left\{ \ u \, \boldsymbol{:} \, \Omega_{T} \to \mathbb{R} \ \ \middle\vert \ \ \left[ \ \begin{aligned} & \forall \, t \in \left( 0 ,\, T \right] \, \boldsymbol{,} \\[0pt] & u \left( \, \boldsymbol{\cdot} \, ,\, t \right) \in C^{2} \left( \Omega \right) \end{aligned} \ \right] \ \ \textsf{かつ} \ \ \left[ \ \begin{aligned} & \forall \, x \in \Omega \, \boldsymbol{,} \\[0pt] & u \left( x ,\, \boldsymbol{\cdot} \, \right) \in C^{1} \left( \left( 0 ,\, T \right] \right) \end{aligned} \ \right] \ \right\} \end{aligned} \end{align}
である。
${}$
任意の $r > 0$ に対して，
\begin{align}
\qquad
\begin{aligned}
E \left( r \right)
:=
E \left( \boldsymbol{0} ,\, 0 \, ; \, r \right)
\, \boldsymbol{,}
\qquad
\varphi \left( r \right)
:=
\dfrac{1}{r^{N}}
\iint_{E \left( r \right)}
u \left( y ,\, s \right)
\dfrac{\left| y \right|^{2}}{s^{2}}
\, dy \, ds
\end{aligned}
\end{align}
とする。
${}$
${}$
4. 熱方程式の境界値
$g \in C^{0} \left( \mathbb{R}^{N} \right) \cap L^{\infty} \left( \mathbb{R}^{N} \right)$ とし，関数 $u \, \boldsymbol{:} \, \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \to \mathbb{R}$ を，
\begin{align}
\qquad
\begin{aligned}
u \left( x ,\, t \right)
:=
\int_{\mathbb{R}^{N}} \Psi \left( x-y ,\, t \right) \cdot g \left( y \right) \, dy
\qquad
\left(
\
\forall
\left( x ,\, t \right)
\in
\mathbb{R}^{N} \times \left( 0 ,\, \infty \right)
\
\right)
\end{aligned}
\end{align}
により定める。このとき，
\begin{align}
\quad
&
\begin{aligned}
\textsf{(1)}
\quad
u \in C^{\infty} \left( \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \right)
\, \boldsymbol{;}
\end{aligned}
\\[5pt]
&
\begin{aligned}
\textsf{(2)}
\quad
\dfrac{\partial u}{\partial t} \left( x ,\, t \right) - \Delta u \left( x ,\, t \right) = 0
\qquad
\left(
\
\forall
\left( x ,\, t \right)
\in
\mathbb{R}^{N} \times \left( 0 ,\, \infty \right)
\
\right)
\, \boldsymbol{;}
\end{aligned}
\\[7.5pt]
&
\begin{aligned}
\textsf{(3)}
\quad
\forall \, x^{0} \in \mathbb{R}^{N} \, \boldsymbol{,}
\quad
\lim_{ \left( x ,\, t \right) \to \left( x^{0} ,\, 0 \right) } u \left( x ,\, t \right)
=
\lim_{ t \to +0 } u \left( x^{0} ,\, t \right)
=
g \left( x^{0} \right)
\end{aligned}
\end{align}
が成り立つ。
- $
\displaystyle
\Psi \in C^{\infty} \left( \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \right)
$ および $u$ の定義から，$
\displaystyle
u \in C^{\infty} \left( \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \right)
$ となる。
${}$ - $
\displaystyle
\Psi \in C^{\infty} \left( \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \right)
$ かつ $
\displaystyle
g \in C^{0} \left( \mathbb{R}^{N} \right) \cap L^{\infty} \left( \mathbb{R}^{N} \right)
$ より，任意の $x \in \mathbb{R}^{N}\boldsymbol{,} \ \ t > 0$ に対して，
\begin{align} \qquad & \begin{aligned} \int_{\mathbb{R}^{N}} \left| \dfrac{\partial}{\partial t} \left\{ \Psi \left( x-y ,\, t \right) \cdot g \left( y \right) \right\} \right| \, dy &\leq \left\| g \right\|_{L^{\infty} \left( \mathbb{R}^{N} \right)} \int_{\mathbb{R}^{N}} \left| \dfrac{\partial}{\partial t} \left\{ \Psi \left( x-y ,\, t \right) \right\} \right| \, dy \\[5pt] &\leq \left\| g \right\|_{L^{\infty} \left( \mathbb{R}^{N} \right)} \left\{ \dfrac{N}{2t} \int_{\mathbb{R}^{N}} \Psi \left( x-y ,\, t \right) \, dy + \dfrac{1}{4t^{2}} \int_{\mathbb{R}^{N}} \left| x-y \right|^{2} \cdot \Psi \left( x-y ,\, t \right) \, dy \right\} \\[5pt] &= \left\| g \right\|_{L^{\infty} \left( \mathbb{R}^{N} \right)} \left\{ \dfrac{N}{2t} + \dfrac{1}{4t^{2}} \int_{\mathbb{R}^{N}} \left| x-y \right|^{2} \cdot \Psi \left( x-y ,\, t \right) \, dy \right\} \\[5pt] &< + \infty \, \boldsymbol{,} \end{aligned} \\[10pt] & \begin{aligned} \int_{\mathbb{R}^{N}} \biggl| \Delta_{x} \left\{ \Psi \left( x-y ,\, t \right) \cdot g \left( y \right) \right\} \biggr| \, dy &= \int_{\mathbb{R}^{N}} \left| \dfrac{\partial}{\partial t} \left\{ \Psi \left( x-y ,\, t \right) \cdot g \left( y \right) \right\} \right| \, dy < + \infty \end{aligned} \end{align}
となるので，偏微分作用素 $\dfrac{\partial}{\partial t} - \Delta$ と積分 $\displaystyle \int_{\mathbb{R}^{N}} dy$ の順序交換可能性から，
\begin{align} \qquad \begin{aligned} \dfrac{\partial u}{\partial t} \left( x ,\, t \right) - \Delta u \left( x ,\, t \right) &= \left( \dfrac{\partial}{\partial t} - \Delta \right) u \left( x ,\, t \right) \\[5pt] &= \left( \dfrac{\partial}{\partial t} - \Delta_{x} \right) \int_{\mathbb{R}^{N}} \Psi \left( x-y ,\, t \right) \cdot g \left( y \right) \, dy \\[5pt] &= \int_{\mathbb{R}^{N}} \left\{ \left( \dfrac{\partial}{\partial t} - \Delta_{x} \right) \Psi \left( x-y ,\, t \right) \right\} \cdot g \left( y \right) \, dy \\[5pt] &= \int_{\mathbb{R}^{N}} \left\{ \dfrac{\partial \Psi}{\partial t} \left( x-y ,\, t \right) - \Delta_{x} \Psi \left( x-y ,\, t \right) \right\} \cdot g \left( y \right) \, dy \\[5pt] &= \int_{\mathbb{R}^{N}} 0 \cdot g \left( y \right) \, dy \\[5pt] &= 0 \, \boldsymbol{.} \end{aligned} \end{align}
${}$ - $x^{0} \in \mathbb{R}^{N}$ を任意に固定する。また，$\varepsilon > 0$ が与えられたとする。
${}$
$g$ の連続性より，
\begin{align} \qquad \begin{aligned} \exists \, \delta_{1} > 0 \ \boldsymbol{;} \quad \forall \, y \in B \left( x^{0} ,\, \delta_{1} \right) \, \boldsymbol{,} \qquad \left| g \left( y \right) - g \left( x^{0} \right) \right| < \dfrac{\varepsilon}{2} \, \boldsymbol{.} \end{aligned} \tag*{\textsf{[1]}} \end{align}
${}$
任意の $x \in \mathbb{R}^{N} \boldsymbol{,} \ \ t > 0$ に対して，
\begin{align} \qquad \begin{aligned} \left| u \left( x ,\, t \right) - g \left( x^{0} \right) \right| &= \left| \int_{\mathbb{R}^{N}} \Psi \left( x-y ,\, t \right) \left\{ g \left( y \right) - g \left( x^{0} \right) \right\} \, dy \right| \\[5pt] &\leq \int_{\mathbb{R}^{N}} \Psi \left( x-y ,\, t \right) \left| g \left( y \right) - g \left( x^{0} \right) \right| \, dy \\[5pt] &= \int_{B \left( x^{0} ,\, \delta_{1} \right)} \Psi \left( x-y ,\, t \right) \left| g \left( y \right) - g \left( x^{0} \right) \right| \, dy \\[5pt] &{\qquad \qquad}+ \int_{\mathbb{R}^{N} \setminus B \left( x^{0} ,\, \delta_{1} \right)} \Psi \left( x-y ,\, t \right) \left| g \left( y \right) - g \left( x^{0} \right) \right| \, dy \, \boldsymbol{.} \end{aligned} \tag*{\textsf{[2]}} \end{align}
${}$
ここで，
\begin{align} \qquad \begin{aligned} & I := \int_{B \left( x^{0} ,\, \delta_{1} \right)} \Psi \left( x-y ,\, t \right) \cdot \left| g \left( y \right) - g \left( x^{0} \right) \right| \, dy \, \boldsymbol{,} \\[5pt] & J := \int_{\mathbb{R}^{N} \setminus B \left( x^{0} ,\, \delta_{1} \right)} \Psi \left( x-y ,\, t \right) \cdot \left| g \left( y \right) - g \left( x^{0} \right) \right| \, dy \, \boldsymbol{.} \end{aligned} \end{align}
と置く。
${}$
$\textsf{[1]}$ より，任意の $x \in B \left( x^{0} ,\, \dfrac{\delta_{1}}{2} \right) \, \boldsymbol{,} \ \ t > 0$ に対して，
\begin{align} \qquad \begin{aligned} \left| I \right| &\leq \int_{B \left( x^{0} ,\, \delta_{1} \right)} \Psi \left( x-y ,\, t \right) \cdot \dfrac{\varepsilon}{2} \, dy \\[5pt] &< \int_{ \mathbb{R}^{N} } \Psi \left( x-y ,\, t \right) \cdot \dfrac{\varepsilon}{2} \, dy \\[5pt] &= \dfrac{\varepsilon}{2} \cdot \int_{ \mathbb{R}^{N} } \Psi \left( y ,\, t \right) \, dy \\[5pt] &= \dfrac{\varepsilon}{2} \cdot 1 \\[5pt] &= \dfrac{\varepsilon}{2} \, \boldsymbol{.} \end{aligned} \tag*{\textsf{[3]}} \end{align}
${}$
さらに，任意の $ \displaystyle x \in B \left( x^{0} ,\, \dfrac{\delta_{1}}{2} \right) \boldsymbol{,} \ \ \ y \in \mathbb{R}^{N} \setminus B \left( x^{0} ,\, \delta_{1} \right) $ に対して，
\begin{align} \qquad \begin{aligned} \left| y - x^{0} \right| \leq \left| y - x \right| + \left| x - x^{0} \right| < \left| y - x \right| + \frac{\delta_{1}}{2} \leq \left| y - x \right| + \frac{1}{2} \left| y - x^{0} \right| \end{aligned} \end{align}
であるので，
\begin{align} \qquad \begin{aligned} \left| y - x \right| > \frac{1}{2} \left| y - x^{0} \right| \, \boldsymbol{.} \end{aligned} \tag*{\textsf{[4]}} \end{align}
${}$
![不等式 !FORMULA[99][-78529560][0] を平面的に表した図](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FsrzOsYfP5hXlynqUpwzC.png?alt=media)
不等式 $\textsf{[4]}$ を平面的に表した図
${}$
$C := \dfrac{2 \left\| g \right\|_{L^{\infty} \left( \mathbb{R}^{N} \right)}}{\left( 4 \pi \right)^{\frac{N}{2}}} \geq 0 \, \boldsymbol{,} \ \ \delta > 0$ とする。任意の $t > 0$ に対して，
\begin{align} \qquad \begin{aligned} 0 < t < \delta^{4} \quad \Longleftrightarrow \quad \sqrt{t} < \delta^{2} \quad \Longleftrightarrow \quad \dfrac{1}{\delta} < \dfrac{\delta}{\sqrt{t}} \end{aligned} \end{align}
であることに注意すると，
\begin{align} \qquad & \begin{aligned} \exists \, \delta_{2} > 0 \ \boldsymbol{;} \qquad \forall \, t \in \left( 0 ,\, \delta_{2}^{4} \right) \, \boldsymbol{,} \end{aligned} \\[10pt] & \begin{aligned} \int_{\mathbb{R}^{N} \setminus B \left( \boldsymbol{0} ,\, \dfrac{\delta_{2}}{\sqrt{t}} \right)} e^{- \dfrac{\left| z \right|^{2}}{16}} \, dz \leq \int_{\mathbb{R}^{N} \setminus B \left( \boldsymbol{0} ,\, \dfrac{1}{\delta_{2}} \right)} e^{- \dfrac{\left| z \right|^{2}}{16}} \, dz < \dfrac{\varepsilon}{2} \cdot \dfrac{1}{C + 1} \, \boldsymbol{.} \end{aligned} \tag*{\textsf{[5]}} \end{align}
${}$
![不等式 !FORMULA[106][-78499769][0] を平面的に表した図](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FD11pgNnO88oYFxF06Y2F.png?alt=media)
不等式 $\textsf{[5]}$ を平面的に表した図
${}$
よって，$\delta := \min \left\{ \delta_{1} ,\, \delta_{2} \right\}$ とすると，$\textsf{[4]} ,\ \textsf{[5]}$ より，任意の $x \in B \left( x^{0} ,\, \dfrac{\delta}{2} \right) \, \boldsymbol{,} \ \ t \in \left( 0 ,\, \delta^{4} \right)$ に対して，
\begin{align} \qquad \begin{aligned} \left| J \right| &\leq 2 \left\| g \right\|_{L^{\infty} \left( \mathbb{R}^{N} \right)} \cdot \int_{\mathbb{R}^{N} \setminus B \left( x^{0} ,\, \delta \right)} \Psi \left( x-y ,\, t \right) \, dy \\[5pt] &= 2 \left\| g \right\|_{L^{\infty} \left( \mathbb{R}^{N} \right)} \cdot \left( 4 \pi t \right)^{- \dfrac{N}{2}} \cdot \int_{\mathbb{R}^{N} \setminus B \left( x^{0} ,\, \delta \right)} e^{- \dfrac{\left| y-x \right|^{2}}{4t}} \, dy \\[5pt] &\leq 2 \left\| g \right\|_{L^{\infty} \left( \mathbb{R}^{N} \right)} \cdot \left( 4 \pi t \right)^{- \dfrac{N}{2}} \cdot \int_{\mathbb{R}^{N} \setminus B \left( x^{0} ,\, \delta \right)} e^{- \dfrac{\left| y - x^{0} \right|^{2}}{16t}} \, dy \\[5pt] &= \dfrac{2 \left\| g \right\|_{L^{\infty} \left( \mathbb{R}^{N} \right)}}{\left( 4 \pi \right)^{\dfrac{N}{2}}} \cdot t^{- \dfrac{N}{2}} \cdot \int_{\mathbb{R}^{N} \setminus B \left( \boldsymbol{0} ,\, \dfrac{\delta}{\sqrt{t}} \right)} e^{- \dfrac{\left| z \right|^{2}}{16}} \cdot t^{\dfrac{N}{2}} \, dz \quad \quad \left( \ \textsf{$z = \dfrac{y - x^{0}}{\sqrt{t}}$ として変数変換} \ \right) \\[5pt] &\leq C \int_{\mathbb{R}^{N} \setminus B \left( \boldsymbol{0} ,\, \dfrac{1}{\delta} \right)} e^{- \dfrac{\left| z \right|^{2}}{16}} \, dz \\[5pt] &\leq \dfrac{\varepsilon}{2} \cdot \dfrac{C}{C + 1} \\[5pt] &< \dfrac{\varepsilon}{2} \, \boldsymbol{.} \end{aligned} \tag*{\textsf{[6]}} \end{align}
${}$
したがって，$\textsf{[2]} ,\ \textsf{[3]} ,\ \textsf{[6]}$ より，任意の $x \in B \left( x^{0} ,\, \dfrac{\delta}{2} \right) \, \boldsymbol{,} \ \ t \in \left( 0 ,\, \delta^{4} \right)$ に対して，
\begin{align} \qquad \begin{aligned} \left| u \left( x ,\, t \right) - g \left( x^{0} \right) \right| = I + J < \dfrac{\varepsilon}{2} + \dfrac{\varepsilon}{2} = \varepsilon \end{aligned} \end{align}
となるので，
\begin{align} \qquad \begin{aligned} \lim_{ \left( x ,\, t \right) \to \left( x^{0} ,\, 0 \right) } u \left( x ,\, t \right) = \lim_{ t \to +0 } u \left( x^{0} ,\, t \right) = g \left( x^{0} \right) \, \boldsymbol{.} \end{aligned} \end{align}
${}$
5. 非斉次熱方程式の解
$f \in C_{0}^{0} \left( \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \right) \cap C^{2 ,\, 1} \left( \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \right)$ とし，関数 $u \, \boldsymbol{:} \, \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \to \mathbb{R}$ を，
\begin{align}
\qquad
\begin{aligned}
u \left( x ,\, t \right)
:=
\int_{0}^{t} \int_{\mathbb{R}^{N}}
\Psi \left( x - y \, , \, t - s \right) \cdot f \left( y ,\, s \right)
\, dy \, ds
\qquad
\left(
\
\forall
\left( x ,\, t \right)
\in
\mathbb{R}^{N} \times \left( 0 ,\, \infty \right)
\
\right)
\end{aligned}
\end{align}
により定める。このとき，
\begin{align}
\quad
&
\begin{aligned}
\textsf{(1)}
\quad
u \in C^{\infty} \left( \mathbb{R}^{N} \times \left( 0 ,\, \infty \right) \right)
\, \boldsymbol{;}
\end{aligned}
\\[5pt]
&
\begin{aligned}
\textsf{(2)}
\quad
\dfrac{\partial u}{\partial t} \left( x ,\, t \right) - \Delta u \left( x ,\, t \right)
=
f \left( x ,\, t \right)
\qquad
\left(
\
\forall
\left( x ,\, t \right)
\in
\mathbb{R}^{N} \times \left( 0 ,\, \infty \right)
\
\right)
\end{aligned}
\\[7.5pt]
&
\begin{aligned}
\textsf{(3)}
\quad
\forall \, x^{0} \in \mathbb{R}^{N} \, \boldsymbol{,}
\quad
\lim_{ \left( x ,\, t \right) \to \left( x^{0} ,\, 0 \right) } u \left( x ,\, t \right)
=
\lim_{ t \to +0 } u \left( x^{0} ,\, t \right)
=
0
\end{aligned}
\end{align}
が成り立つ。
- .
\begin{align} \quad & \begin{aligned} . \end{aligned} \end{align}
${}$ - .
\begin{align} \quad & \begin{aligned} . \end{aligned} \end{align}
${}$ - .
\begin{align} \quad & \begin{aligned} . \end{aligned} \end{align}
${}$
この記事を高評価した人
この記事に送られたバッジ
投稿者
