文献あり

向きがある=裏表がある？

はじめに

多様体やトポロジーを学んでいると, どこかの段階で向きの概念について習います. 「向き付けられない図形」の代表格である「メビウスの帯」は, 子供の頃に作ったことがあるという方も多いでしょう. このあまりにも身近な例の特徴から, 向きの付けられない図形のことを「裏表の区別がない図形」というイメージを持たれた, あるいはそのように説明されたことがある方も少なくないのではないでしょうか.

ひととおりの幾何学(多様体論)を学んでふと振り返ると, ある時次のような疑問が湧いてきました.

しばしば同列に語られる「向き付け可能性」と「裏表の区別の有無」は, 果たして本当に同じ概念だろうか?

今回は空間の中に置かれた曲面に対し, 定義の復習や具体例を通してこのテーマを考えていくことにします.

※本稿では, 多様体は全て連結かつ第２可算公理を満たすものとします.

向きと裏表

多様体の向き

はじめに, 多様体の向き付け可能性について復習しておきましょう.

多様体の向き

多様体$M^m$上の空でない共通部分を持つ2つの座標近傍$(U; x^1, \ldots, x^m)$と$(V; y^1, \ldots, y^m)$が同じ向きであるとは, $U\cap V$上で変換のJacobi行列式が
\begin{align} \det{\left(\frac{\partial(y^1, \ldots, y^m)}{\partial(x^1, \ldots, x^m)}\right)}>0 \end{align}
を満たすことをいう.
多様体$M$が向き付け可能(orientable)であるとは, $M$の座標近傍系で, どの2つの空でない共通部分を持つ座標近傍も同じ向きであるようなものが存在することをいう.
多様体の向きのイメージ

このように, もともと多様体の向きは, 局所座標をいくつ貼り合わせていっても座標の向きの整合性が保たれることでもって定義されていました. メビウスの帯が向き付け不可能なのは, 座標近傍をぐるりと一周させるとその向きが逆になってしまうからです.

また, 有名な射影平面$\mbb{RP}^2$にも向きが入らないことは, 下図のように$\mbb{RP}^2$にはメビウスの帯の構造が含まれていることから理解できます.
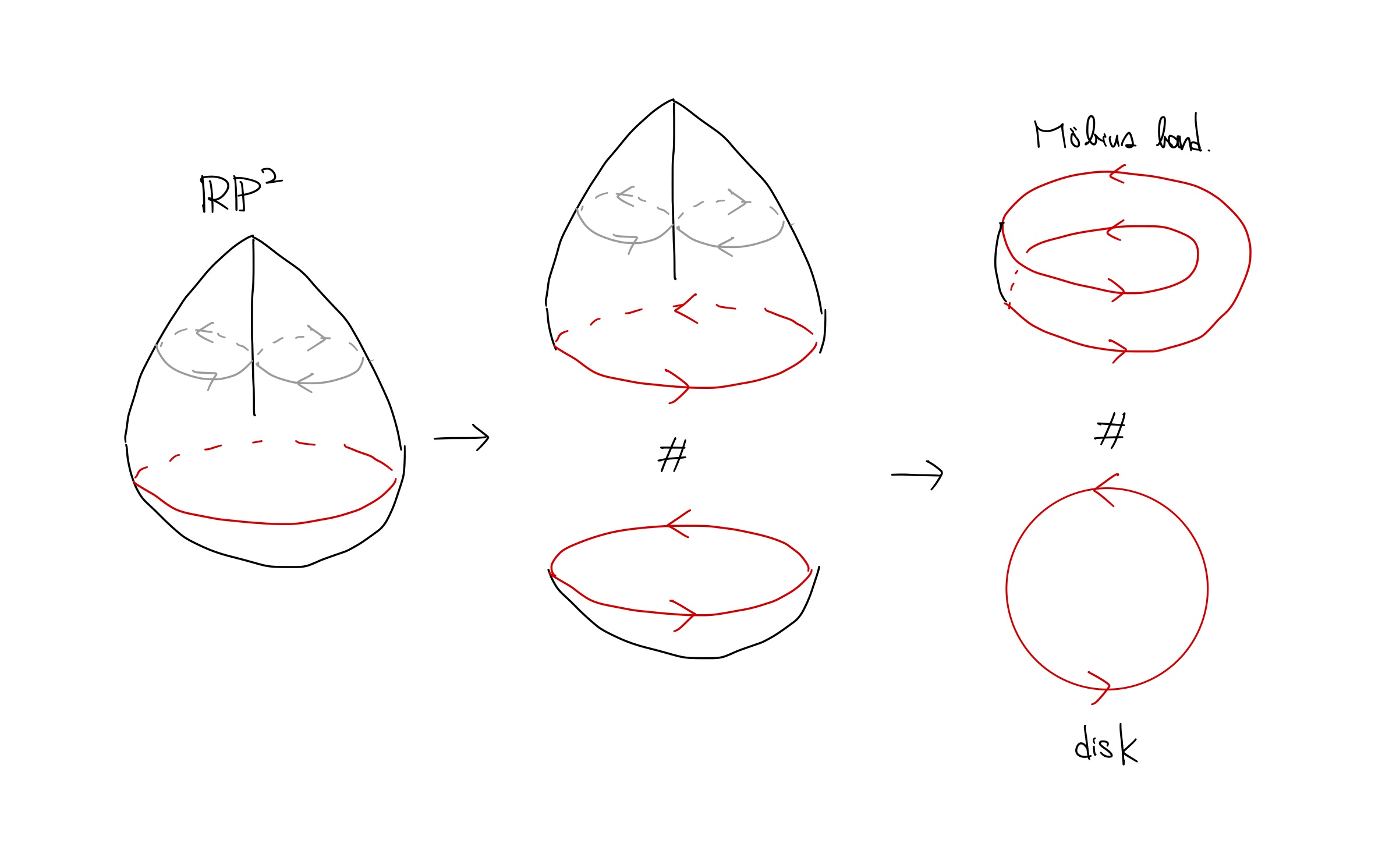2次元射影空間の分解

多様体の向き付け可能性は, 次のように微分形式を用いて定式化することもできます.

微分形式による向きの定式化

多様体$M^m$に対し, 以下は同値である.
(1) $M$は向き付け可能.
(2) $M$上の$m$次微分形式$\omega$で, $\omega = 0$となる点を持たないようなものが存在する.

証明は, 例えばMMYやMSYを参照してください.

微分形式を使ったことによってより際立つのは, 多様体の向きの定義が$M$の幾何学的な情報だけによることです. 仮に$M$が別の空間内の部分多様体だったとしても, 向き付け可能性は外側の空間の情報に関係なく決まります. こうした意味で、向き付け可能性は内在的(intrinsic)な概念であると言えます.

そもそも「裏表」とは？

ここまでで多様体の向き付けの定義について見てきました. メビウスの帯に裏表が無かったり, 向き付け不可能な多様体にはメビウスの帯の構造が含まれていたりと, 「向きがある＝裏表がある」という感覚は今のところ間違ってないように思います. ですがそもそもの話, 我々は図形の裏表をまだ数学的に定義していません. では, 図形の裏表って一体何なのでしょうか?

通常我々は, 空間の中に置かれた図形を外から見ることを通してその裏表を認識します. ですので本来, 裏表というものは, ある多様体にはめ込まれた部分多様体に対して定義される概念のはずです.

ところで, 曲面論なんかで次のような向きの定義を見たことがある方も多いのではないでしょうか.

曲面の向き

$\Sigma$を$\mbb{R}^3$内に(はめ込まれた)曲面とする.
(1) 曲面$\Sigma$に沿ったベクトル場$N$で, $\Sigma$の任意の接ベクトル場$X$に対して$\inn{X}{N}=0$となるものを$\Sigma$の法ベクトル場という.
(2) 曲面$\Sigma$上に長さ$1$の法ベクトル場(単位法ベクトル場)が大域的に定義できるとき, 曲面$\Sigma$は「向き付け可能」であるという.

先に定義した向きとは区別する意味で「」を付けました.

こちらの定義によれば, 法ベクトルの向いている方向が表, そうでない方が裏という風に, より直感に沿った意味で裏表が考えられそうです.

そこで今回は, この「向き」の定義をベースに, 超曲面(余次元1の部分多様体)の裏表を次のように定義しましょう.

超曲面の裏表

Riemann多様体$M$内の超曲面$\Sigma$に裏表の区別がある(two-sided)とは, $\Sigma$上に連続な単位法ベクトル場が存在することを言う. そのような単位法ベクトル場が存在しないとき, すなわち任意の単位法ベクトル場が零点を持つとき, $\Sigma$には裏表の区別がない(one-sided)と言う.
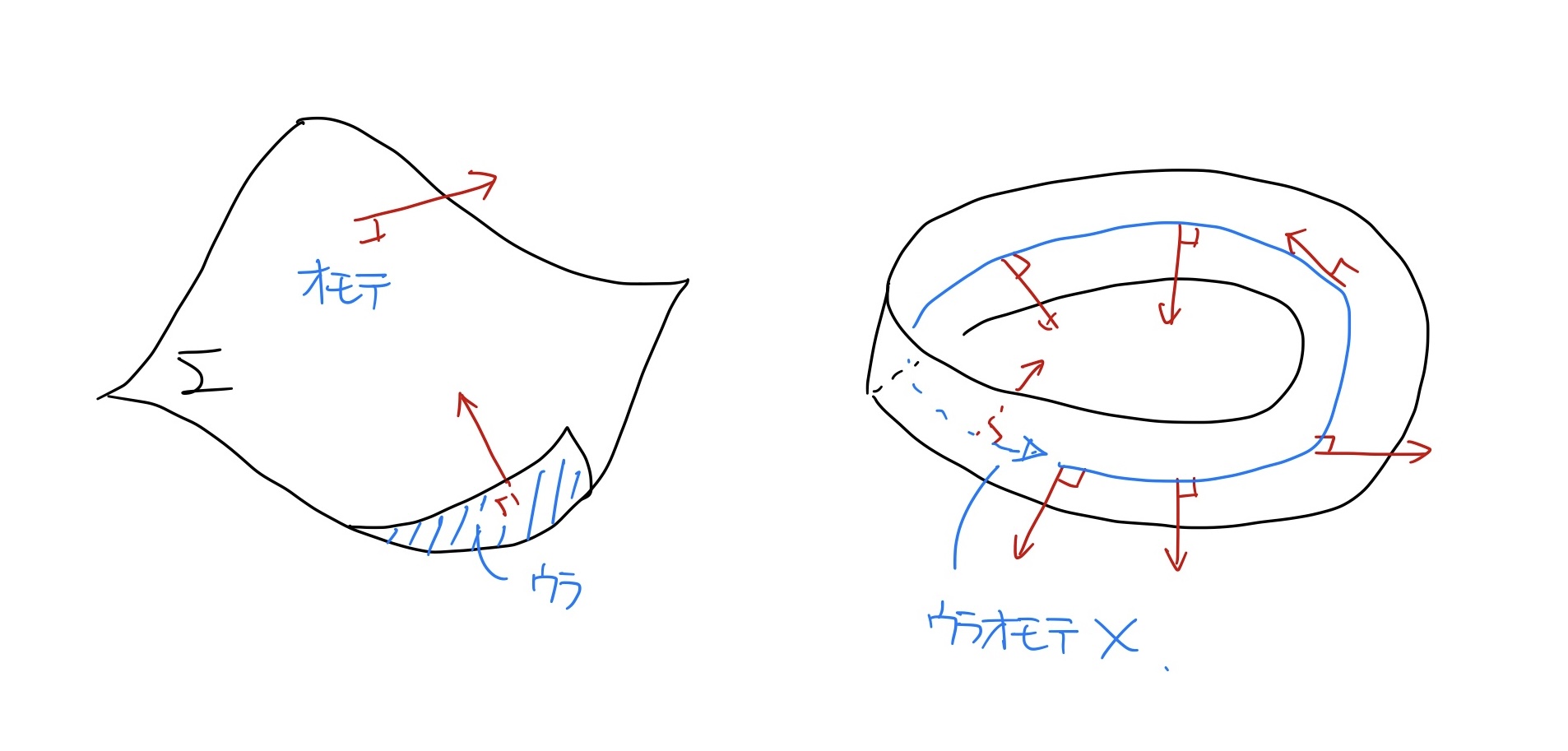単位法ベクトルの存在に基づく裏表のイメージ

ベクトル束の言葉を使うなら, この定義は「超曲面$\Sigma$の法束(normal bundle)が自明」と言い換えられます. ですので, $M$上に計量の存在を仮定せずとも, 裏表の概念は(整合性を保ったまま)定義できます. 今回は直感的なわかりやすさを優先して, 計量の存在を仮定する定義を採用しました.

さて, 裏表の概念が定義できたところで, 冒頭の問いを改めて定式化しましょう.

超曲面において, 「向き付け可能性」と「裏表の区別の有無」は同値だろうか?

実は向き付け可能な多様体に対しては, その中の超曲面の向き付け可能性と裏表の有無の概念は一致します.

向き付け可能ならば向きと裏表は同じ

$M^{n+1}$を向き付け可能なRiemann多様体とし, $\Sigma^n$を超曲面とする. このとき, 以下は同値である.
(1) $\Sigma$は向き付け可能.
(2) $\Sigma$には裏表の区別がある.

$M$は向き付け可能だから, $M$上の$(n+1)$次微分形式$\Omega$で, 至る所$0$にならないものが存在する.
超曲面$\Sigma$上の法ベクトル場$N$に対し, $\Sigma$上の$n$次微分形式$\omega$を次で定義する:
\begin{align} \omega_p(X_1, \ldots, X_n) = \Omega_p(X_1, \ldots, X_n, N), \quad X_1, \ldots, X_n \in T_p\Sigma. \end{align}
$\Omega$の取り方から, $\omega$がある点$p \in \Sigma$で$0$になるための必要十分条件は$N_p = 0$となることだから, 定理1より
$\Sigma$が向き付け不可能$\iff$$\Sigma$に裏表の区別がない
となる. 対偶を考えると, $\Sigma$の向き付け可能性と裏表の有無は同値になる.

それでは向き付け不可能な多様体の場合はどうでしょうか? 少し考えると, 一般には向きと裏表の両者は一致しないであろうと結論づけられます. と言うのも, 先ほど例に挙げたメビウスの帯と, その中にセンターラインとして埋め込まれた円周$\mbb{S}^1$がまさしく反例になっているからです. 円周それ自体は向き付け可能ですが, 法ベクトル場をぐるりと一周させると逆向きになってしまいますから, 裏表の区別をつけることはできません.

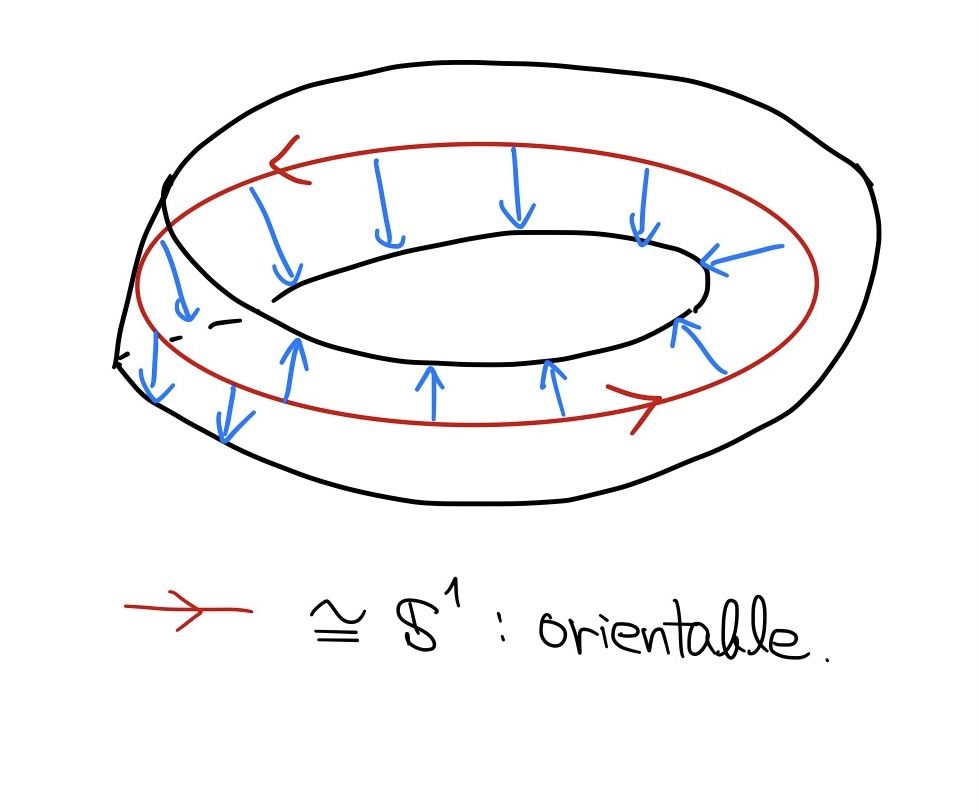メビウスの帯のセンターラインは向き付けられるが裏表の区別はない

このように、今回考えた裏表の概念は, 超曲面が多様体のなかでどのように置かれているかに依存します. 内在的だった向きの概念に対して, このような概念は外在的(extrinsic)であると言われます. 向きと裏表は, 内在的か外在的かという点で決定的な違いがあったのです.

改めて, 冒頭の問いに回答を提示しておきましょう.

超曲面の「向き付け可能性」と(今回定義した)「裏表の区別の有無」は, 前者は多様体の内在的性質に, 後者は外在的要因に依存して決まるため, 一般に異なる概念である.

次節では両者の概念が一致しないような色々な例を見ていきます.

色々な曲面の向き付け可能性と裏表

向きと裏表の違いについて理解したところで, それらが一致しない色々な具体例について考えます.

向き付け×, 裏表×な曲面

はじめに, 向きもつけられないし裏表の区別もないような例を見てみましょう. これは比較的簡単に構成できて, 射影空間$\mbb{RP}^3$の中の$\mbb{RP}^2$を考えればよいです. 3次元射影空間$\mbb{RP}^3$は向き付け可能な多様体ですから, 定理2により向き付けられない$\mbb{RP}^2$には裏表の区別は付けられません.
!FORMULA[63][470008246][0]に埋め込まれた!FORMULA[64][470008215][0] $\mbb{RP}^3$に埋め込まれた$\mbb{RP}^2$

向き付け×, 裏表○な曲面

次に, 向き付けられないけれど裏表の区別はつけられる曲面の例を考えます. 向き付けできない曲面として, 先ほどと同様に射影平面$\mbb{RP}^2$について考えます. これが裏表を持つようにするには, 射影平面と円周の直積$\mbb{RP}^2\times \mbb{S}^1$への埋め込み
\begin{align} \mbb{RP}^2 \to \mbb{RP}\times \{0\} \subset \mbb{RP}^2\times \mbb{S}^1 \end{align}
を考えればよいです. 実際, $\mbb{S}^1$上の単位ベクトル場$v$の$\mbb{RP}^2\times \{0\}$への制限が, 埋め込まれた射影平面の裏表を定めます.
!FORMULA[71][-161324684][0]内の!FORMULA[72][470008215][0] $\mbb{RP}^2\times\mbb{S}^1$内の$\mbb{RP}^2$

向き付け○, 裏表×な曲面

最後に, 向き付けできるけど裏表がない曲面の例を考えます. この例は少し難しいですが, メビウスの帯のセンターラインの例を高次元化するイメージを持つとわかりやすいです.
メビウスの帯の境界に沿って円板を貼り付けると射影平面$\mbb{RP}^2$が得られたことを思い出すと, $\mbb{RP}^2\times \mbb{S}^1$の中の, メビウスの帯のセンターライン$\alpha\subset \mbb{RP}^2$と$\mbb{S}^1$の直積で得られるトーラス$\mbb{T}^2$の埋め込み
\begin{align} \mbb{T}^2 \to \alpha \times \mbb{S}^1 \subset \mbb{RP}^2 \times \mbb{S}^1 \end{align}
が, 求める曲面の例を与えます.
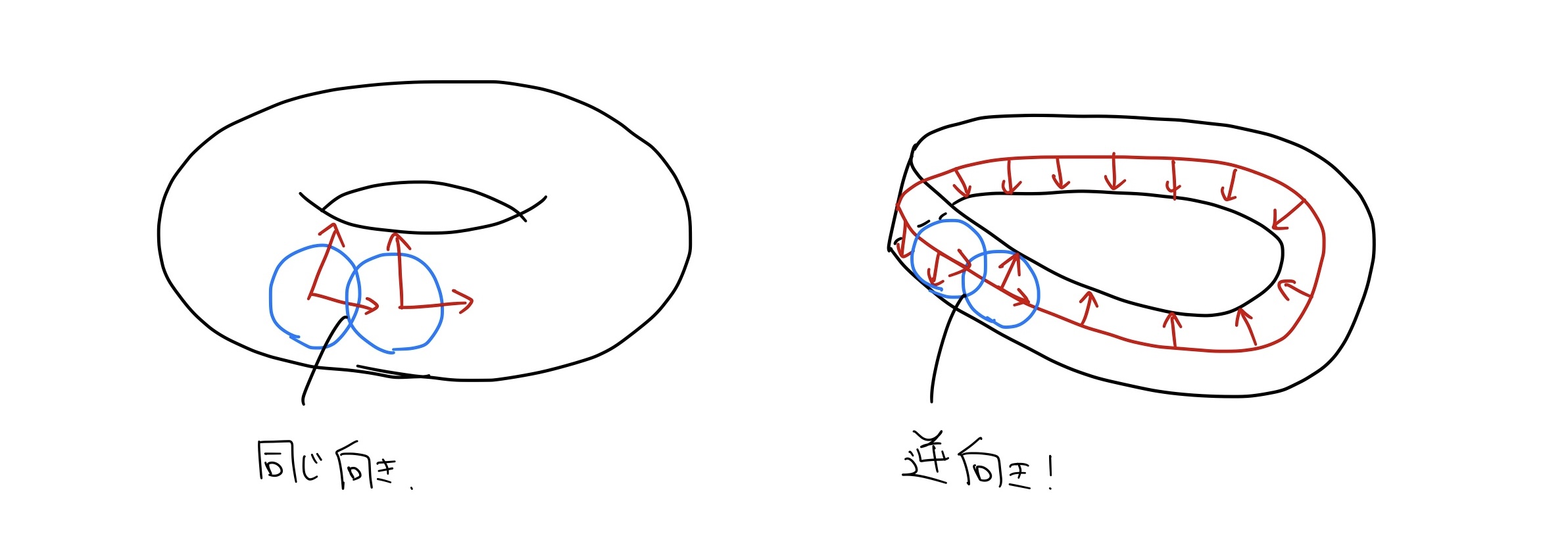
トーラス$\mbb{T}^2$それ自体は, ご存知の通り向き付け可能な多様体です.
一方, このトーラスに直交するベクトルは, $\mbb{RP}^2$上の接ベクトルでセンターライン$\alpha$に直交するものでなければなりませんが, センターラインの裏表の区別の無さからそのようなベクトル場は必ずどこかで$0$になってしまいます. よってトーラス上で連続に定義された単位法ベクトル場は存在しないため, このトーラスには裏表の区別がありません.
!FORMULA[83][-161324684][0]内の!FORMULA[84][-1228607967][0] $\mbb{RP}^2\times\mbb{S}^1$内の$\mbb{T}^2$

おわりに

これまでに見てきたように, 超曲面の向き付け可能性と裏表の区別の有無は, ある意味で全く別の概念であることがわかりました.
超曲面に裏表があるかどうか, すなわち大域的な単位法ベクトル場が存在するかどうかは, 超曲面の変分問題を考える上で重要になります. 標準的な変分問題の教科書では, 向きと裏表の微妙な違いについて触れられたものは少ない(と思われる)ため, この部分で誤解したりつまづいたりしている方々の助けになればと思い, 本記事を執筆するに至りました.

少しでも幾何学って面白いと感じていただければ幸いです.