文献あり

『桜降る代に決闘を』の双掌繚乱の組合せ数の変遷

桜降る代に決闘を

桜降る代に決闘を（通称ふるよに）とは

BakaFire Partyの製作した２人用ボードゲームです。メガミの力を宿す能力者「ミコト」となり、対戦相手との決闘に臨みます。
双掌繚乱、眼前構築、桜花決闘の３ステップが本作の特徴です。
双掌繚乱―あなたが選ぶのは２キャラの組み合わせ
あなたは両手にメガミの力を宿せるため、メガミ２柱のカードを組み合わせられます。同じメガミでも組み合わせる相方次第で戦略が変化し、より幅広いゲームが楽しめます。
眼前構築―相手のキャラを見てからデッキを組む
相手の宿すメガミ２柱を見てから、２２枚から１０枚を選ぶ形でデッキが組めます。自らの強みを貫くか、相手に合わせて構築を変えるか。意思を決定するのはあなたです。
桜花決闘―ボードとトークンを用いた新しい戦い
ボードに３６個の桜花結晶トークンが置かれ、その個数で戦況が表現されます。例えば「間合」に４個の桜花結晶があれば、彼我の距離は４離れているのです。

(出典: 最初に知っておきたいこと |桜降る代に決闘を／公式攻略ページ )

双掌繚乱

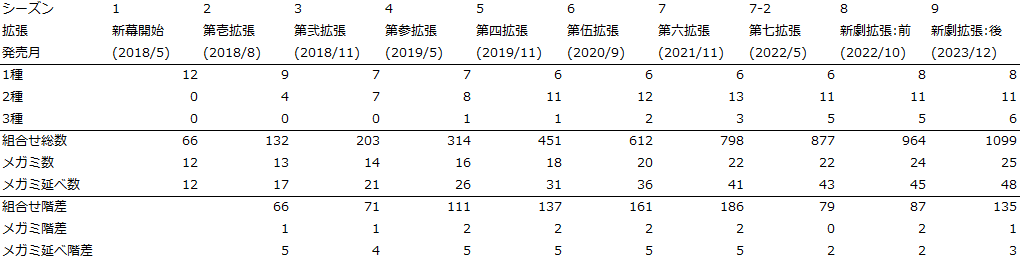
プレイヤーは全$25$柱のメガミのうち$2$柱を選び使用する(2023年12月時点)。
つまり${}_{25}C_2=300$通りの選び方がある$\cdots\cdots$ではこの記事が終わってしまうが、話はそう単純ではない。
$25$柱のうち$17$柱のメガミには「アナザー」と呼ばれる別バージョンがある。さらに、うち6柱は「アナザー」を$2$種類持っている。

同じメガミ同士を組み合わせることはできない。つまり、「メガミ甲のオリジンとメガミ甲のアナザー」という組み合わせはできない。

違うメガミ同士なら組み合わせることができる。つまり「メガミ甲のオリジンとメガミ乙のアナザー」や「メガミ甲のアナザーとメガミ乙のアナザー」などは可能である。

この双掌繚乱には何通りの組み合わせがあるのだろうか。
また、何度かの拡張のたびにメガミは増えてきた。それに伴って組合せの数がどのように増えてきたかを見てみよう。

組み合わせの計算

(具体的な数値での計算はこちらの記事をご覧ください。以下の文字による議論よりはわかりやすいと思います。)

バージョンを$i$種類持っているメガミの数を$x_i$とする。

バージョン数$i$種類$\times$バージョン数$j$種類のメガミで双掌繚乱するときの組合せを考える。

(i)$i\ne j$のとき
まず、メガミの組合せは$x_ix_j$通りある。このそれぞれに対して、$ij$通りのバージョンの組み合わせがある。よって$ijx_ix_j$通りの組合せがある。

(ii)$i=j$のとき
メガミの組合せは$\combi{x_i}{2}$通りあり、このそれぞれに対して、$i^2$通りのバージョンの組合せがある。よって$\combi{x_i}{2}i^2$通りの組合せがある。

したがって、現在は3種類のバージョンを持つメガミが最大だから、

\begin{align*} \sum_{i=1}^{2}\sum_{j=i+1}^{3}ijx_ix_j+\sum_{i=1}^{3}\combi{x_i}{2}i^2&=2x_1x_2+3x_1x_3+6x_2x_3+\combi{x_1}{2}+4\combi{x_2}{2}+9\combi{x_3}{2}\ \ \text{通り} \end{align*}

となる。