自然数のかけ算の交換法則を図で説明してみる

よく話題になる算数のかけ算の数の順番

Twitter(現X)でいつも話題になるものとして、掛け算の順番がある。
時折、小学校の低学年の算数のテスト問題で、順番が逆だとかでバツにされた回答が話題になる。
小学校の算数なのだから、主に自然数（$0$以上整数）だと思われるが、
$m,n$:自然数や整数や有理数、実数、複素数の場合のかけ算で交換法則
$m \times n = n \times m$
が成り立つ。
行列や四元数、文字列の結合などでは交換法則は成り立たないが、それと自然数や整数や有理数、実数、複素数で交換法則は成り立つこととは無関係である。
また、偉い人が言ったからなどは理由にはならない。
自然数のかけ算で、交換法則が成り立つことは、$m$本の平行線とそれぞれ交わる$n$本の平行線を描いた時の交点の数が積（掛け算の結果）$mn$なので明らかだが、なぜかそれで納得しない層もいる。
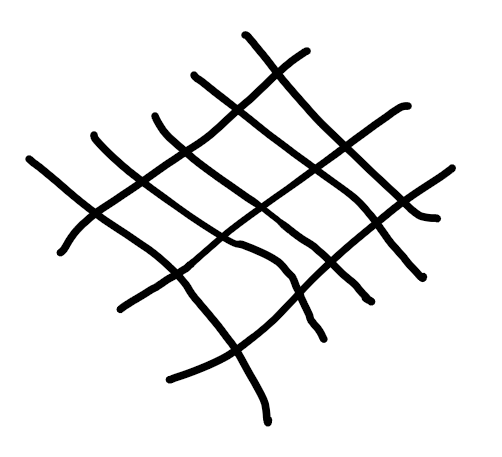交わる2組の平行線
実数のかけ算などでは交換法則も定義に含める場合もあるが、基本的には定義には含めずとも定義から交換法則が成り立つことは導ける。
以前、$0$以上の整数（自然数）とたし算、かけ算の定義して、たし算とかけ算の交換法則を導くツイートをした。

Xで自然数の算数の掛け算の順序の話題とかよく見かけるので、LaTeXの練習で、改めて自然数を定義してみて、たし算とかけ算の交換法則を示してみたけどあってるかな。。https://t.co/zFDmiU9mwx pic.twitter.com/2uP7TjmKsr

— IIJIMAS (@IIJIMAS) April 1, 2024

$0$を含む自然数の定義する

$0$は自然数に含まれるとする。
$S$を自然数から別の（既存のものではない）自然数を作り出すものとする。（結果的にできる自然数全体から自然数全体への写像となる。後者写像と呼ばれる。$0$が像にはならず全射ではない。）
$0$をもとにすべて異なる数を作り出す。
$1:=S0$
$2:=S1=SS0$
$3:=S2=SS1=SSS0$
$4:=S3=SS2=SSS1=SSSS0$
$$ \cdots $$
と定義して、その数全体$\{0,1,2,3,4,...\}$を$\mathbb{N}$で表し「自然数全体」と呼ぶ。
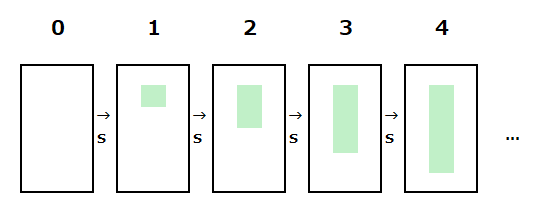自然数全体

たし算の定義

たし算を
$$n + 0 := n$$
$$n + Sm := S(n+m)$$
と定義する。
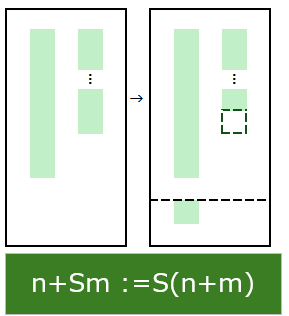たし算の定義

かけ算の定義

かけ算を
$$n \times 0 := 0 $$
$$n \times Sm := n \times m + n $$
と定義する。
図では、$n \times m$に対応するものは、縦の長さ$n \times m$で横の長さ$1$の縦長の長方形だが、以下の議論では面積の同じ縦の長さ$n$横の長さ$m$の長方形で表す。(この理由は後で示すことの先取りだが、$n \times m$が$n+n+ \cdots +n \quad \cdots $ $m$個の$n $の和と同じであることによる。 )

注意：長方形の90度回転で明らかだが、以下の議論で一貫しているのならば縦の長さm横の長さ$n$の長方形と入れ替えても（すべてで同様に置き換えるのなら）問題ない。

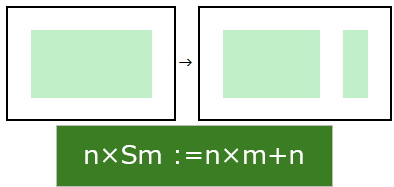かけ算の定義

前者写像$S^{-1}$を定義する

$0$以外で$S$の逆写像になるとなる、$S^{-1}: \mathbb{N} \longrightarrow \mathbb{N}$を
$$S^{-1}0:=0$$
$$S^{-1}Sn:=n$$
となるものとして定義する。$0$だけ$0$と$1$の像なので単射ではない。

また、$S$と$S^{-1}$について、以下のような略記する
$$S^n0=SSS \cdots S0$$
（右辺は$S$が$n$個）

$n \leq z$に対して
$$S^{-n}z=S^{-1}S^{-1} \cdots S^{-1}z$$
（右辺は$S^{-1}$が$n$個）

$1 \times m=1+1+\cdots+1=m$

$1 \times m $
$= 1 \times S^{-1}m + 1 $
$= 1 \times S^{-2}m + 1 + 1 $
$$ \cdots $$
$= 1 \times S^{-m}m + 1 + 1 $
$= 1 \times 0 + 1 + 1 + \cdots + 1 \cdots$($1$が$m$個)

$= 0 + 1 + 1 + \cdots + 1$
$= 1 + 1 + \cdots + 1$
$= 1 + S0 + \cdots + S0$
$= 2 +S0 +\cdots + S0 \cdots $ ($S0$が$m-2$個)
$\cdots$
$= m$
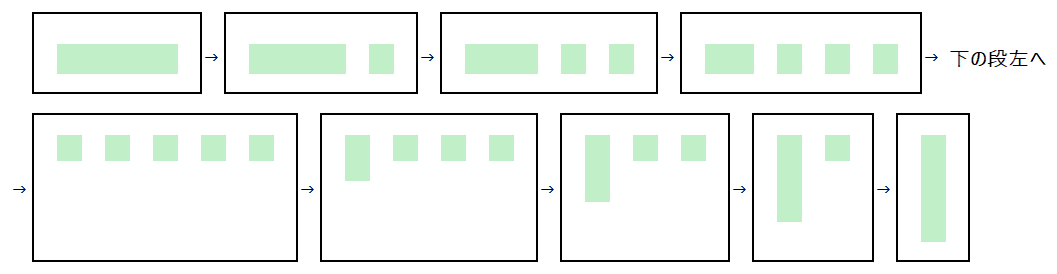1×m=m

たし算の交換法則($n+m=m+n$)

$n+m$
$=S(n+S^{-1}m)$
$=SS(n+S^{-2}m)$
$\cdots$
$=S^m(n+S^{-m}m)$
$=S^m(n+0)$
$=S^m(n)$
$=S^m(S^n0)$
$=S^{m+n}0$
$\cdots$
$=m+n$
よって$n+m=m+n $が示された。
たし算の交換法則($n+m=m+n$)

$n \times m = n+n+ \cdots +n \quad(m個のnの和)$

$n \times m$
$=n \times S^{-1}m+n $
$=n \times S^{-2}m+n+n $
$=n \times S^{-3}m+n+n+n $
$\cdots$
$=n \times S^{-m}m+n+n+\cdots +n \quad\quad (m個のnの和)$
$=n \times 0+n+n+\cdots +n \quad\quad (m個のnの和)$
$=0+n+n+\cdots +n \quad\quad (m個のnの和)$
$=n+n+\cdots +n \quad\quad (m個のnの和)$
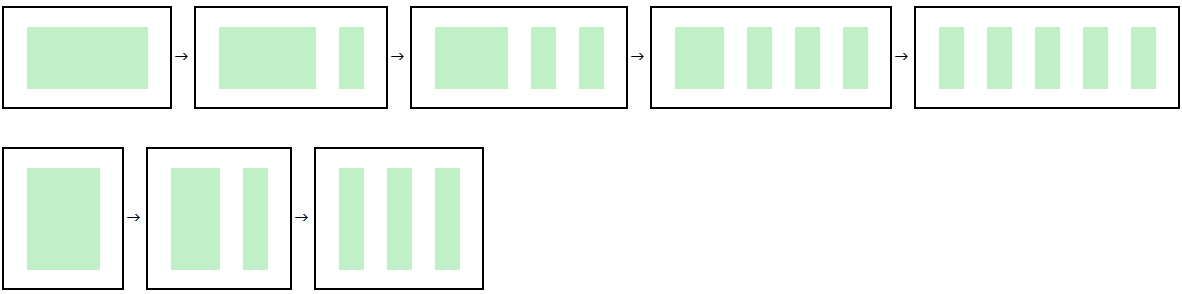積を和で表した図、上段は3×5,下段は5×3

かけ算の交換法則($m \times n=n \times m$)

上で示したことにより、
$m \times n$
$=m+m+\cdots+m \quad\quad (mをn個の和)$
$=(S^{-1}m+1)+(S^{-1}m+1)+\cdots +(S^{-1}m+1) \quad\quad $
たし算の交換法則を繰り返して
$m \times n$
$=(S^{-1}m+S^{-1}m+\cdots +S^{-1}m)+(1+1+\cdots +1) $
（それぞれ$n$個の和）
$S^{-1}m+S^{-1}m+\cdots +S^{-1}m=S^{-1}m \times n $であり、
前に示した$1+1+\cdots +1=n$を使って、
$m \times n$
$=S^{-1}m \times n+n $
これを繰り返して、
$m \times n$
$=S^{-2}m \times n+n+n $
$\cdots$
$=S^{-m}m \times n+(n+n+\cdots +n) \quad (第2項はm個のnの和)$
$=0 \times n+ (n \times m)$
$=0 \times (S^{-1}n+0)+ (n \times m)$
$=0 \times (S^{-2}n+0)+ (n \times m)$
$\cdots$
$=0 \times (S^{-n}n+0)+ (n \times m)$
$=0 \times (0+0)+ (n \times m)$
$=0 \times 0+ (n \times m)$
$=0+ (n \times m)$
$=n \times m$
よって$m \times n=n \times m$が示された。
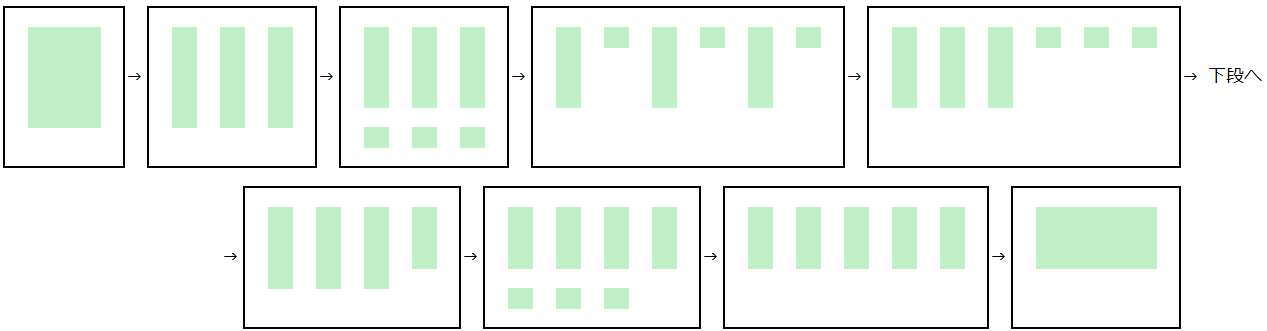かけ算の交換法則 5×3=3×5

まとめ

長方形に並べたものの個数は90度回転しても変わらないのは直観的に明らかだが、
直観に頼らず、交換法則を最初から成り立つと定めなくても、自然数の積について交換法則が成り立つことを導くことができた。