院解12 京大数学系 H25 数学I 5 複素関数の広義積分

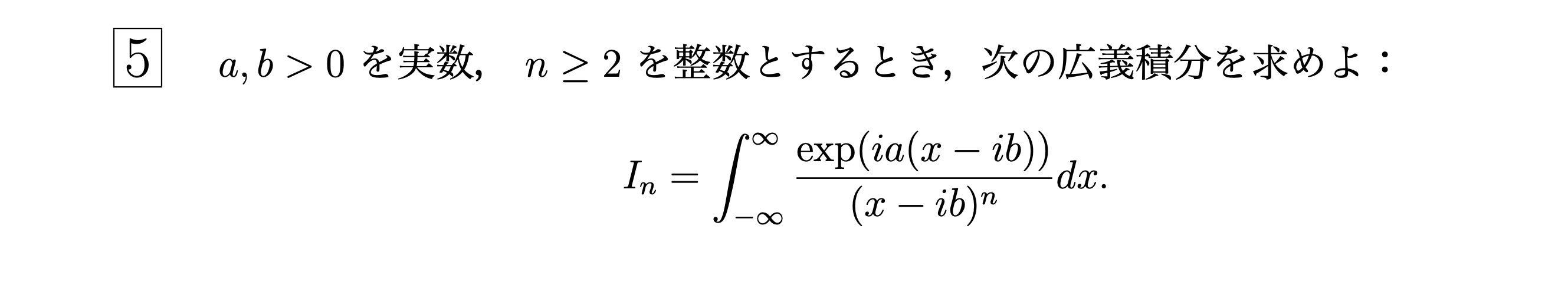
$f(z)=\dfrac{\text{exp}ia(z-ib)}{(z-ib)^n}$とおく.$R>4b$として図のような積分路をとる.

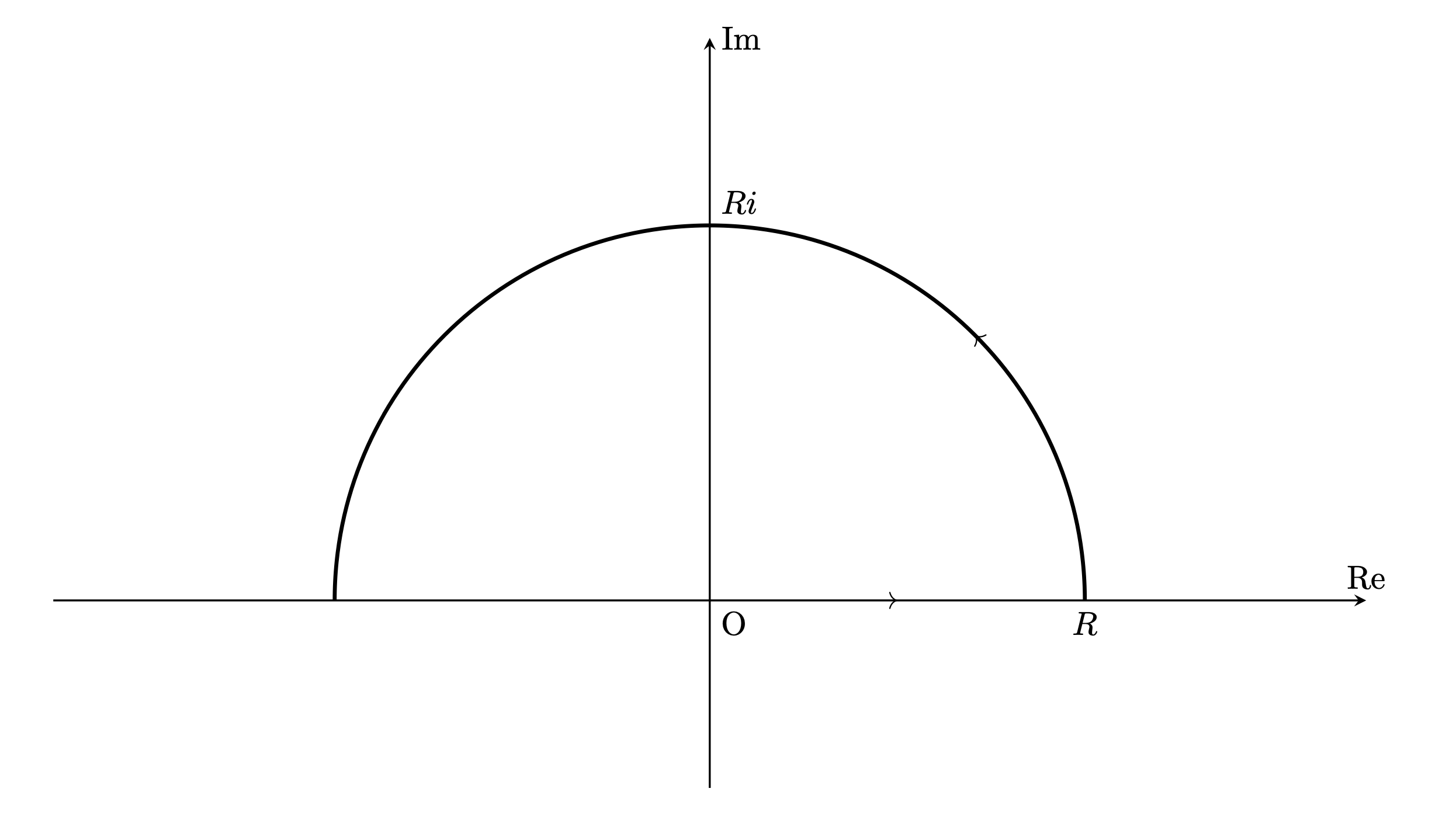
経路のうち実軸上の部分,円周の一部になっている部分をそれぞれ$L_1,L_2$とおく.
$\left|\displaystyle\int_{L_2} f(z)dz\right|\leq \displaystyle\int_{L_2}\left|f(z)\right||dz|=\displaystyle \int_0^1 \left| \dfrac{\text{exp}(ia(Re^{i\pi t}-ib))}{(Re^{i\pi t}-ib)^n}\right|\cdot R\ dt$
$\leq \displaystyle \int_0^1 \dfrac{e^{ab}e^{-aR\text{sin}\pi t}}{(R^2-2bR\text{sin}\pi t+b^2)^{\frac{n}{2}}}\cdot R\ dt\leq \dfrac{e^{ab}}{\left(\dfrac{\sqrt{3}}{2}R\right)^{n-1}}\to0\ ,(R\to\infty)$.
留数定理から
$\displaystyle\int_{L_1}f(z)dz+\displaystyle\int_{L_2}f(z)dz=2\pi i\text{Res}(f,ib)$ここで$R\to \infty$として
$\displaystyle\int_{-\infty}^\infty \dfrac{\text{exp}(ia(x-ib))}{(x-ib)^n}dx=2\pi i\text{Res}(f,ib)$ .$ib$は$n$位の極だから
$\text{Res}(f,ib)=\displaystyle\lim_{z\to ib} \frac{d^{n-1}}{dz^{n-1}}\text{exp}(ia(z-ib))=(ia)^{n-1}$.よって
$(\text{与式})=2\pi i(ia)^{n-1}$.$\Box$