発散級数で積分を解く
発散級数を使って積分を解く
どうも、らららです。
今回はこの積分を示していきます。
$$\int_{0}^{\infty}\frac{x}{\sinh x}dx=\frac{\pi^2}4$$
(ちなみにこの積分を考えたのは余余余氏が積分・級数botのある積分の証明として投稿したこの ツイート の最後の式変形)
この積分はまめけびさんのこの記事で 記事 でフルヴィッツのゼータ関数の積分表示を用いて証明させているがこの記事では留数定理と発散級数を用いて解いていく。
発散級数を収束させる
私は発散級数の収束については詳しくないので間違ったことを書いてるかもしれません。
もし間違ったことを書いていたらコメントで指摘してくれると助かります。
保険をかけたところで発散級数を収束させていきます。
$$\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}\quad(\mathrm{Re}(s)>1)$$
この級数は$\mathrm{Rs}(s)>1$で収束します
リーマンゼータ関数は解析接続という方法により全ての複素数$s$で定義できます。
これにより$\di\zeta(-1)=-\frac1{12}$となることが知られてます。
ここで級数表示に$s=-1$を代入してみると$\di\sum_{n=1}^{\infty}n=-\frac1{12}$となります。
和の形にすると$\di1+2+3+\cdots=-\frac1{12}$となります。
もちろんこの級数は発散します。
しかし発散以外に意味を持たせるとしたら$\di-\frac1{12}$という値に収束させることができます。
これが発散級数を収束させるということです。
$$\eta(s)=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^s}\quad(\mathrm{Re}(s)>1)$$
偶奇を分けて計算することで$\di\eta(s)=\left(1-2^{1-s}\right)\zeta(s)$が得られます。
$\di1-2^{1-s}$も$\zeta(s)$も全ての複素数$s$で定義されるので$\eta(s)$も全ての複素数$s$で定義できます。
$\di\eta(s)=\left(1-2^{1-s}\right)\zeta(s)$を用いて$\di\eta(s)=\frac14$となることが分かります。
先ほどと同じ方法で$\di\sum_{n=1}^{\infty}n(-1)^{n-1}=\frac14$となります。
発散級数を収束させることができました。
ちなみにこの級数が発散することの証明はダランベールの収束判定法を用いれば発散することが示せる
解く
留数定理、やりましょう!
\begin{align}
I&=\int_{0}^{\infty}\frac{x}{\sinh x}dx
\\&=\int_{-\infty}^{\infty}\frac{x}{e^x-e^{-x}}dx
\end{align}
$\di f(z)=\frac{z}{e^z-e^{-z}}$として以下の経路で積分する。
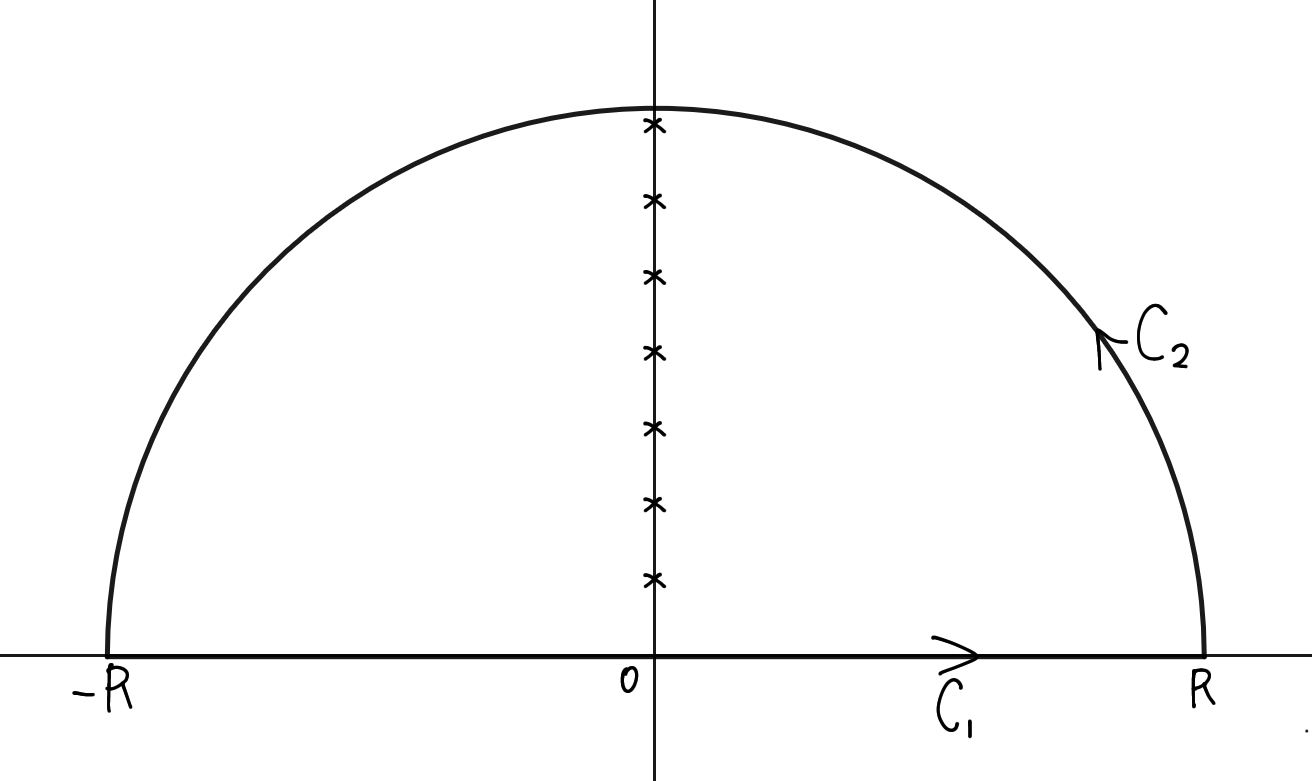 積分経路
積分経路
虚軸上に×があるのは(分母)$\neq0$となる$z$を考えれば
$e^z+e^{-z}=0$となり解くと$z=i\pi n(n\in\mathbb{Z})$となるので虚軸に特異点の印として×が等間隔に並んでいます。
また$z=0$で×が書かれていないのは極限をとると
\begin{align}
\lim_{z\to0}\frac{z}{e^z-e^{-z}}
&=\lim_{z\to0}\frac{1}{e^z+e^{-z}}
\\&=\frac12
\end{align}
となり解析的には特異点として考えなくてもいいことになります。
全体の積分を$C$としてそれぞれ積分を計算していきます。
\begin{align}
\int_{C_1}f(z)dz
&=\int_{-R}^{R}f(z)dz
\\&=2\int_{0}^{R}f(x)dx
\\&=I\quad(R\to\infty)
\end{align}
そのまま$I$になりますね
\begin{align}
\int_{C_2}f(z)dz&=0\quad(R\to\infty)
\end{align}
$0$になることの証明は読者への課題とする。
これは不等式評価で示せる。
全体の積分は留数定理を用いて
\begin{align}
\oint_{C}f(z)dz&=2\pi i\sum_{n=1}^{\infty}\underset{z=i\pi n}{\mathrm{Res}}f(z)
\\&=2\pi i\sum_{n=1}^{\infty}\lim_{z\to i\pi n}\frac{z}{e^z+e^{-z}}
\\&=\pi^2\sum_{n=1}^{\infty}n(-1)^{n-1}
\\&=\frac{\pi^2}4
\end{align}
$$\oint_C=\int_{C_1}+\int_{C_2}$$
$$I=\frac{\pi^2}4$$
でたーー!!
でましたね
一般化できそうなので一般化しましょう
一般化
$$\int_{0}^{\infty}\frac{x^{2n+1}}{\sinh x}dx=\frac{\left(2^{2n+1}-1\right)\pi^{2n+2}B_{2n+2}}{2n+2}$$
証明の方法は先ほどとほとんど同じです
$\di\zeta(-n)=-\frac{B_{n+1}}{n+1}$を用いればできます
\begin{align}
\eta(-2n-1)&=\left(1-2^{2n+2}\right)\zeta(-2n-1)
\\&=\frac{\left(2^{2n+2}-1\right)B_{2n+2}}{2n+2}
\end{align}
あとは先ほどの留数計算のようにやればできます。
おわりに
発散級数を通していますが発散級数を収束させるとこで積分を解くことができました。
実際、この積分の値は正しいです。
この方法で正しい積分が得られたのは偶然ではなく必然だと思ってます、なでこの方法で積分が求まるのか知ってる方がいたら教えてほしいです。
発散級数を通して積分を解く方法、いろいろ見つけたいです
ちなみにこの
ツイート
で一例が提示されている。
おしまい!!
