JMO2023予選参加記
はじめに
JMO2023の予選に参加したので参加記を書こうと思います.
もう3ヵ月経ったって本当?
予選問題のネタバレを含みます.
試験前
試験一カ月前~一週間前
とにかくJMO・JJMOとOMCの問題を漁って解いていました. 解いているときは気づきませんけどやっぱり良問が多いですよね. (AIMEとか良いかもしれません)
おすすめ問
鋭角三角形$ABC$について,その垂心を$H$,外心を$O$とする.$$AH=AO, OH=12, BH=5$$
のとき,線分$CH$の長さを求めよ.
$3$桁の正の整数について,ちょうど$1$桁を変えて得られる$7$の倍数の個数をその整数の$\textbf{ラッキー度}$とよぶ.$100$以上$999$以下の整数全てに対して,そのラッキー度の総和を求めよ.
OMCは楽しいので皆さん是非やりましょう(宣伝) OMCのサイト
一週間前~前日
試験が近づくたびに焦りがつのっていました.まあBランク取れたらいいかなーみたいなことを考えていました.3日前ぐらいには,JJMO2022の問題を時間測って解いたりしていました.
試験前は自信をつけないとパフォーマンスが落ちる(個人差)ので,自分のこれまでの良かった記録を眺めることをおすすめします.
試験当日
ヤバいです。緊張が止まりません。水をめっちゃ飲んでいました.特に誰と話すわけでもないので,本当に緊張がほぐれません.30分ぐらい早く着いたので,頭の中で今日の夜ご飯を考えたりしていました.(結局体調のせいでそんなに食べれなかった)
10~15分前ぐらい?には人がぞろぞろと入ってきて,結構賑やかになりました.
試験開始
(ここからは解いてるときの思考を書いています)
パッと見た感じ6,7,8が地雷っぽくてこわい 絶対沼るやつじゃん...
→ 1 $10×(平方数)$を小さい順に試す→解ける
→ 2 めんどくさそう... でも差は怪しすぎるのでさすがに対称性→解ける
→ 3 相似 終わり
→ 4 これOMCであったよ(後述) →解ける
→ 見直し(特に2)
→ 5に行く→いろいろ考えるが解けない
→ 6に行く→解けない
→ 7に行く→$(a-\dfrac{1}{b})(a-\dfrac{1}{c})=2023$を思い付くが進まない
→ 5,6,7 を同時並行で考える
→ 5 $d_k=a_{k+1}-a_k$とおいてみる→$d_{k+1}$と$d_k$の関係式がつくれる!→解ける むずくないか...?
→ 6,7 を同時並行で考える
→ 7 さっきの式から$a=45$が分かるじゃん... →$(2b-45)(2c-45)=2023$で終わり
→ 6 粘る → 天から補助線が降ってくる →一発ゲー過ぎて不安になる
→ 7完すれば受かるだろうと踏む(これは本当によくないですやめましょう)
そのため念入りに見直しする
→ 9,10に手をつける→よく分からん
→ 8 めっちゃ実験する よくよく考えたら偶奇だけ考えたら良いのね
→ (続き) 線分が良いか悪いかを先に埋めて考えてみる→$M=15$か?
→ 五角形の中は少なくとも$1$つ悪くなる!→$M=17$で決め方も分かる→厳密性がよくわからないけど時間がないのでとりあえず答えを書く
→最後に見直しをしっかりする
試験後
満面の笑みでした.そもそも7完で受かるだろうに自称8完しているので,多分受かるだろう(フラグ)し,落ちてもボーダー-1だと思ったので,去年3点だった私としては大満足です.
どうでもいいですがこのあと風邪引きました
問題ごとの感想 (1~8)
文字数稼ぎ
ちゃんとした分かりやすい解説はMetachickさんが書かれていたので,是非読んで下さい.↓
https://mathlog.info/articles/3894
問題をちゃんと書くのはめんどくさいので雑に書きます
1 (分野 : N)
$n+10$と$10n$がともに平方数となる最小の正整数$n$は?
式で解こうとするとペル方程式になるんですかね(あまり詳しくない).「最小」を見たときは一番最初に「必要条件で順に試す」を考えるといいと思います.$n=10k^2$($k$は整数)が必要条件となります.
試し方はいろいろあると思いますが,例えば$n=k^2-10 ~ (k=4,5,\ldots)$を試してもいいと思います.ですが$10k^2$の方が速く増加するので今回だとそっちの方が良いかなとは思いました.まあ最悪$n=1,2,\ldots$です
2 (分野 : C)
正の整数であって(十進法表記で)各位に$3$の数より$2$の数の方が多いものを$\textbf{良い数}$,少ないものを$\textbf{悪い数}$とよぶ.
$2023$以下の良い数の個数と$2023$以下の悪い数の個数の差は?
この問題のポイントは"差"です.さすがに意味もなくこれを置くはずがありません.そこで,「どこか打ち消し合うのでは?」と考えます.
この問題では対称性が使えます.こう聞くと難しそうですが,「良い数と悪い数の定義の仕方ほとんど一緒だよね」という考えです.まあ$2$と$3$を入れ替えただけですからね.
また,$1$から$1999$までと$2000$から$2023$に分けることで$1$から$1999$までを打ち消すことができます(これは区切りのいいところで分けようという考えなので割と自然な発想だと思います).あとは$2000$から$2023$を丁寧に数えあげると終わります.
ちなみにですが,それぞれの個数を求めてもそんなに計算重くなさそうです.(そっちで解いた人も一定数いそう)
3 (分野 : G)
一辺の長さが$3$の正三角形$ABC$の辺$BC,AC,AB$上にそれぞれ点$D,E,F$がある.
$$AD=1, ∠ADE=∠DEF=60^{\circ}$$
のとき,$AF$の長さは?
図が汚すぎる
まず,フリーハンドでもいいので図を書き直した方がいいと思います.普通に見にくいので...
角度計算をすると相似がめっちゃ出てきます.そもそもこの相似は結構よく出てくるもので,覚えても良いような気がしています.あとは適当に辺の比を計算することで解くことができます.
めっちゃ個人的な意見なんですが,これ最易じゃないですか...?
4 (分野 : A)
$x*y=\dfrac{x}{xy+1}$と定義するとき,
$$((( \cdots (((100*99)*98)*97)* \cdots )*3)*2)*1$$
を計算せよ.
これ面白いですよね.いろいろな解き方があると思います.普通に実験をしても法則が見えてきますし,漸化式とかで体育しても良いと思います.
さて,OMCはすごいです(唐突)。丸々出てきます。
 OMC○○○(○)
OMC○○○(○)
これはOMCの解説の一部分なのですが,なんとこの問題を解くために必要な性質が丸々乗っています.これを左から使っていくことで,問題を解くことができます.
「...いやどうやってそれ思い付くんだよ!」って思った人もいると思います.私なりに考えてみました.
一つは,「$(x*y)*z$を計算してみる」ということです.中の$()$から外してあげたいですからね.するとたまたま$\dfrac{x}{xy+xz+1}=x*(y+z)$になった.そこから計算できる.という感じです.これならまだ現実味があると思います.
もう一つは,「$\dfrac{1}{x*y}$に注目する」です.$\dfrac{1}{x*y}$は$\dfrac{1}{x}+y$という非常にシンプルな式になります.これならこの式が成り立つことも頷けますね.現実味は正直薄いですが,おそらくこれを最初に発見した人はここから発見したんじゃないでしょうか(適当)
というか後から気付きましたが,これを使ったらそのまま問題が解けますね...
5 (分野 : N(A))
$\{a_i\}_{i=1,2,\ldots,7}$は相異なる正の整数列であり,$\{ia_i\}_{i=1,2,\ldots,7}$は等差数列.
$|a_7-a_1|$としてありうる最小の値は?
これ結構難しいと思います... やることは簡単なんですが,どうしてもそれが思い付かないんですよね.
まず,$7$を$3$とか$4$に変えて実験してみましょう.すると,$a_1,a_2,\ldots,a_7$に同じ数を足しても,条件は保たれることが分かると思います.なので,公差を文字でおきたくなると思います(私だけ?).簡単のために,もう$a_1=0$としちゃいます.(正という条件を無視していますが,そんなに関係ないことが簡単に分かります.) まあこれは別にやらなくても大丈夫です.
このとき $a_i=\dfrac{(i-1)×(公差)}{i}$ です.$i-1$と$i$は互いに素なので,公差は$420$の倍数なことが分かって,あとは代入すると終わります.公差を文字でおくのがポイントでした.
公式解説も他の方もこんな感じで解かれていたんですが,私は本番,別の解き方をしたので書きたいと思います.
実はこれのために参加記書いてるまであります
$|a_7-a_1|$があるので,どうしてもその差$d_i=a_{i+1}-a_i ~ (i=1,2,\ldots,6)$を文字でおきたくなりました.
条件は$k=1,2,3,4,5$について,
$$(k+2)a_{k+2}-(k+1)a_{k+1}=(k+1)a_{k+1}-ka_k$$
です.これを変形していくと,
$$(k+2)d_{k+1}+a_{k+1}=(k+1)d_{k}+a_{k}$$
$$(k+2)d_{k+1}=kd_k$$
となります.あとは$1$つの式にまとめるなりすると,解くことができます.
そういえば$a_i=420/i$をエスパーしている方を発見してこわかったです...
6 (分野 : G)
図のように長方形の中に正六角形が内接している.正六角形の面積は?
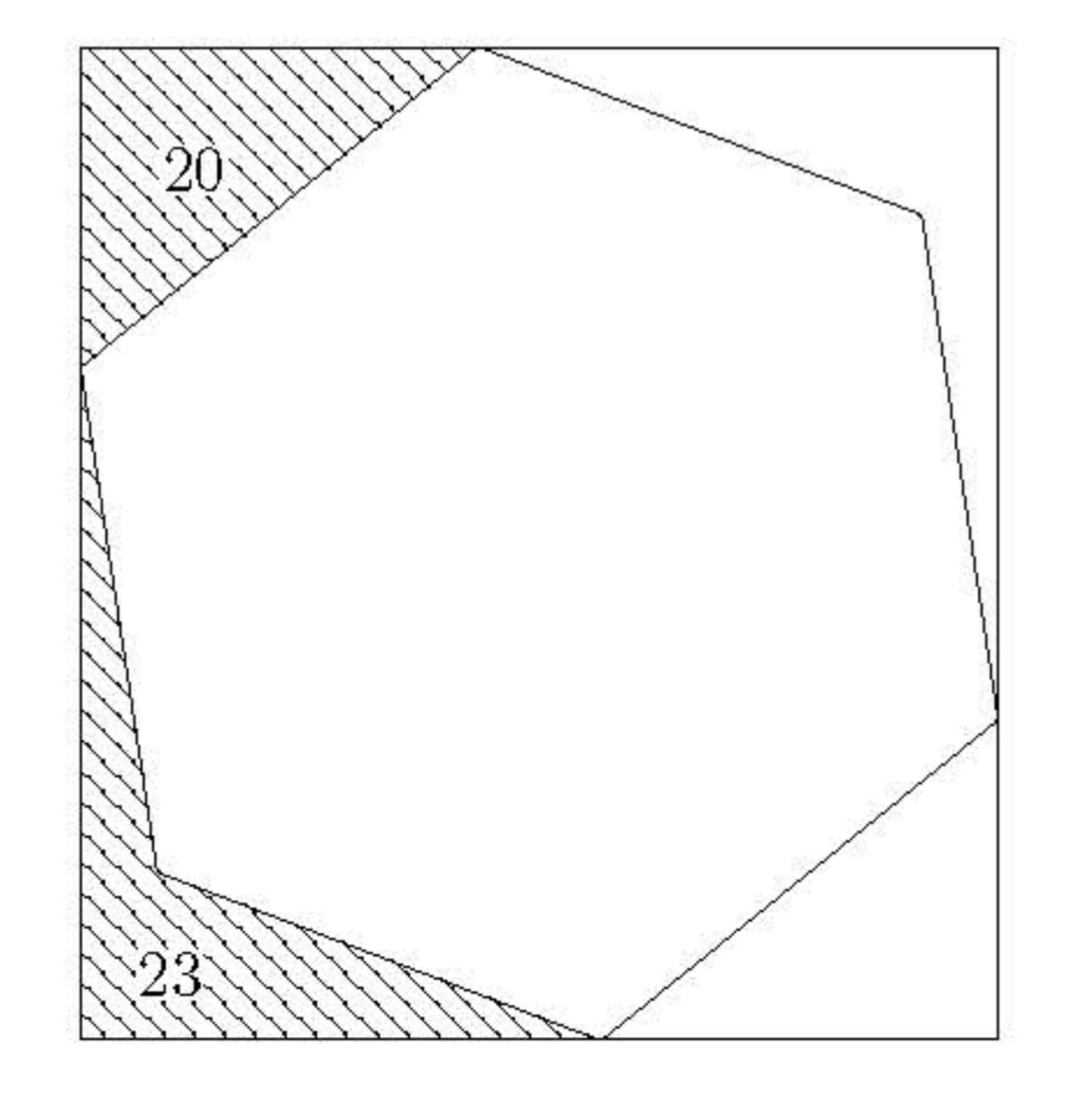 図
図
図形問題です.よくわからないところの面積が与えられているし,長さの情報が全くないです.まずい。
これは何なんでしょうか... 発想一発ゲーだと思います... 降ってくると解けるし,降ってこないと進まないと思います.JJMOっぽい.
↑普段一発ゲーの問題ばっかり作ってる人が言えない
面積の情報だけが出てくるので,相似を見つけようとはなるかもしれませんが... それにしても大分見にくいと思います...
なのに座標でごり押せるらしいですね 体育...
7 (分野 : N)
正の整数の組$(a,b,c)$は,
$$b \leq c, \frac{(ab-1)(ac-1)}{bc}=2023$$
を満たしている.
$c$としてありうる値は?
これ好きです.絞り込み→因数分解の良問で教育的だと思っています.
$((a^2-2023)b-a)((a^2-2023)c-a)=2023$ という因数分解ができることに気づけば「$a$は限られるのでは?」になると思います.$(a-\dfrac{1}{b})(a-\dfrac{1}{c})=2023$はなんで思い付いたんでしょうか.... OMC128-Eみたいなのを解くと良いと思います.
他にも$b$と$ab-1$,$c$と$ac-1$が互いに素なことを使っても解けるそうです.
8 (分野 : C)
下の図のような各頂点に$0,1,2$を書き込み,両端の点に書かれた数の差が$1$の辺を$\textbf{良い辺}$とよぶ.良い辺の個数が最大となるような書き込み方はいくつある?
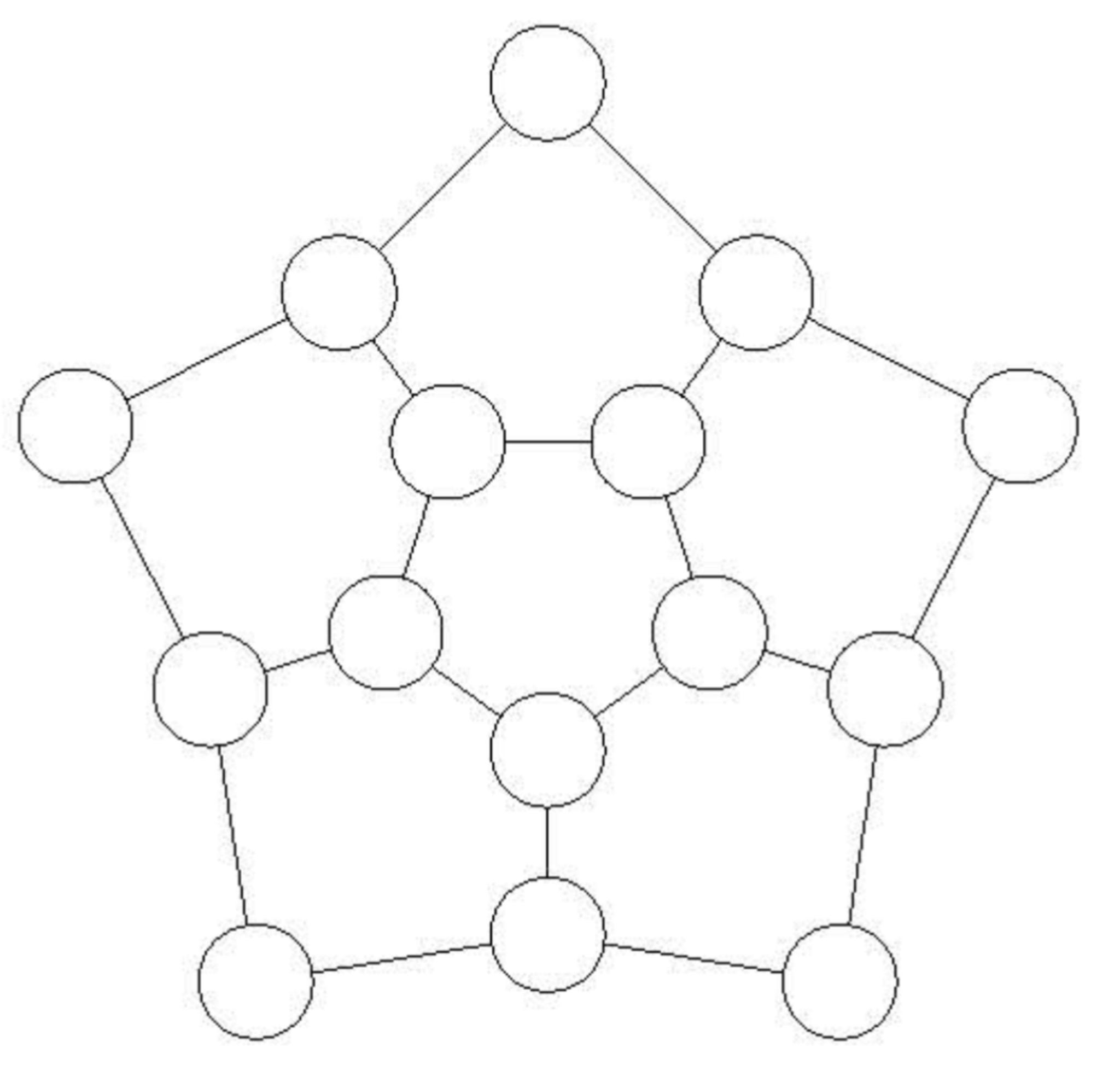 図
図
見た目からJMO2022-6(トラウマ)を思い出しました.これはとにかく実験が大切だと思っています.
頑張ると偶奇だけ見れば良いことが分かったり,輪の中は少なくとも良い辺じゃないものが存在すること(どっちも結構大切)が分かったりします.悪い辺は最大$2$つまで共有できて,どの輪にも悪い辺が存在するので$M \leq 17$がわかります.
$M=17$の個数は辺から決めていくとほぼ一意(正確には5つ)なことが分かるので,あとは適当に答えを求めることができます.楽しい組み合わせだと思いました.
問題ごとのお気持ち(9~12)
9 (分野 : C)
$(1,2,\ldots,2023)$の並び替え$(p_1,p_2,\ldots,p_{2023})$であって
$$p_1+|p_2-p_1|+|p_3-p_2|+\cdots+|p_{2023}-p_{2022}|+p_{2023}=4048$$
を満たすものはいくつある?
解答見ましたがこれめっちゃ良いですね.そりゃ$2023$が含まれるんだから$4046$は超えるに決まってる...
10 (分野 : G)
問題書くのがめんどくさいです
難角問題です.結構特殊で難しそ~になりましたが10の中では簡単みたいです.Vecさんが分かりやすい記事を書かれていたのでそちらを貼っておきます. 私から言うことはありません
https://mathlog.info/articles/3897?s=09
11 (分野 : C?)
よく分かりません.自分が解答欄に何を書いたかも覚えていません.
12 (分野 : A)
よく分かりません.でもとても面白そうな問題だと思いました.
結果
8完でAランクでした!いや嬉しすぎました.全力が出せて本当に良かったです...
でもボーダー8はおかしいでしょ
最後に
...3か月遅れて申し訳ありません.本選も書く予定でしたが普通に8月ぐらいになりそうなので多分書きません.やっぱり記事を書くのは私に向いていない...
最後に,ここまで読んで頂きありがとうございました.
そういえば灘中模試が近付いていますね...
