単純ルートからルート系を構成する
単純ルートからルート系を構成する方法の説明。物理っぽいいいかげんな書き方になっているかもしれませんがご容赦ください。
例外群$\rm G_2$の単純ルートからルート系を具体的に構成します。以下の3つの方法で構成します:
- 逐次的構成
- ディンキン・インデックスを用いた方法
- 随伴表現の最高ウェイトから落として構成
主に参考にした文献はGeorgiKikkawaSatoです。Zeeは群論の物理への応用に関し平易に書かれた入門書です(ただし広範な分野をカバーしているため、ページ数は多いです)。
定義・公式集
まず必要最低限の定義・定理・公式を示しておきます。主にGeorgiの教科書Georgi、ところどころ吉川の教科書Kikkawaを参照しています(ほぼ引用の部分もあります)。証明は付していませんが、それに関してはこれら教科書をご参照ください。またリー代数に関して多少の知識を有していることを想定しています。カルタン生成子、随伴表現、構造定数等の言葉は定義なしに用います。
ウェイト
ウェイトとはカルタン生成子の固有値です:
\begin{align}
\qquad H_i|\mu,x,D\rangle =\mu_i|\mu,x,D\rangle
\end{align}
ここで$H_i\ (i=1,2,\cdots,r)$はカルタン生成子、$r$はランクと呼ばれます。$|\mu,x,D\rangle$は生成子が作用する空間の元ですが、以降これを(量子力学っぽく)「状態」と呼びます。$D$は表現に対するラベルであり、$x$は$\mu$では指定しきれないラベルを表します。随伴表現では$\mu$のみで状態を完全にラベルできるので$x$は必要ありません。
ルート
ルートとは随伴表現のウェイト。任意の生成子を$X_a$とし、これに対応する状態を$|X_a\rangle$と書きます。これはすなわち
\begin{align}
\qquad \langle X_c|X_a|X_b\rangle=[T_a]_{cb}
\end{align}
を意味します。ここで$T_a$は$X_a$に対応する行列表現。随伴表現では
\begin{align}
\qquad \langle X_c|X_a|X_b\rangle=[T_a]_{cb}=-if_{acb}
\end{align}
です。ここで$f_{acb}$は構造定数。この式より、随伴表現では生成子の状態への作用は交換子で表されることを示せます:
\begin{align}
\qquad X_a|X_b\rangle = |[X_a,X_b]\rangle
\end{align}
カルタン生成子$H_i \ (i=1,2,\cdots,r)$に対応する状態はゼロのウェイトをもちます:
\begin{align}
\qquad H_i|H_j\rangle=|[H_i,H_j]\rangle=0
\end{align}
随伴表現ではその逆も成り立ちます:随伴表現においてゼロのウェイトベクトルをもつ状態はすべてカルタン生成子に対応する。
カルタン生成子に対応しない随伴表現の他の生成子を$E$、その状態を$|E\rangle$で表します。これらはゼロでないウェイトベクトル$\boldsymbol{\alpha}$をもちます。そこで$E$を$E_{\boldsymbol{\alpha}}$のようにラベルすることにします。その成分$\alpha_i$は
\begin{align}
\qquad H_i|E_{\alpha}\rangle=\alpha_i|E_{\boldsymbol{\alpha}}\rangle
\end{align}
です。これは対応する生成子が
\begin{align}
\qquad [H_i,E_\boldsymbol{\alpha}]=\alpha_i E_{\boldsymbol{\alpha}}
\end{align}
を満たすことを意味します。
上記したように、随伴表現ではゼロでないウェイトは一意的に対応する状態を指定し、他のパラメータは必要ありません。随伴表現のウェイト$\alpha_i$はルートと呼ばれます。
随伴表現において$|E_{\boldsymbol{\alpha}}\rangle, |H_i\rangle$らはすべて直交します(そうなるように定めることができます)。
昇降演算子
$E_{\pm\boldsymbol{\alpha}}$は、状態$E_{\pm\boldsymbol{\alpha}}|\mu,D\rangle$がウェイト$\boldsymbol{\mu}\pm\boldsymbol{\alpha}$をもつので、ウェイトに対する昇降演算子です。
SU(2)部分代数
\begin{align}
\qquad E^\pm := |\boldsymbol{\alpha}|^{-1}E_{\pm\boldsymbol{\alpha}}
, \ E_3:=|\boldsymbol{\alpha}|^{-2}\boldsymbol{\alpha}\cdot \boldsymbol{H}
\end{align}
とすると、これらはSU(2)部分代数をなします。$|E_3\rangle,|E^\pm\rangle$はスピン1表現をなします。
ルートの正負、順序
各ルート$\boldsymbol{\alpha}$の成分を$(\alpha_1,\alpha_2,\cdots,\alpha_r)$の順に並べたとき、最初のゼロでない成分が正(負)のとき、そのルートを正(負)ルートとよびます。
2つのルート$\boldsymbol{\alpha},\boldsymbol{\beta}$に対して、ベクトル$\boldsymbol{\alpha}-\boldsymbol{\beta}$の最初の$0$でない成分の差$\alpha_i-\beta_i$が正ならば$\boldsymbol{\alpha}>\boldsymbol{\beta}$とします。
単純ルート
単純ルートとは、他の正ルートの和として書けない正ルート。単純ルートは線形独立かつ完全です。よって単純ルートはその代数のランク$r$だけ存在します。次章から行うように、単純ルートがわかれば他のルートを構築することができます。
ルートに関する制限
単純リー代数におけるルートに関し、以下のような制限が存在します:
$\boldsymbol{\alpha},\boldsymbol{\beta}$をルートとする。$n_1,n_2$は非負整数とする。
\begin{align}
\qquad
4\frac{(\boldsymbol{\alpha}\cdot\boldsymbol{\beta})^2}{\boldsymbol{\alpha}^2\boldsymbol{\beta}^2}&=n_1n_2,\\
\frac{\boldsymbol{\beta}^2}{\boldsymbol{\alpha}^2}&=\frac{n_2}{n_1}
\end{align}
とすると、$n_1n_2$、2つのルートの角度$\theta$、大きさの比は以下の表に限られる(Kikkawaの表8-1):
\begin{align}
\qquad
\begin{array}{ccc}
\hline
n_1n_2 & \theta & |\boldsymbol{\alpha}|/|\boldsymbol{\beta}|\\
\hline
0 & 90^\circ & -\\
1 & 60^\circ, 120^\circ & 1\\
2 & 45^\circ, 135^\circ & \sqrt{2},1/\sqrt{2}\\
3 & 30^\circ, 150^\circ & \sqrt{3},1/\sqrt{3}\\
4 & 0^\circ, 180^\circ & -\\
\hline
\end{array}
\end{align}
また以下が成立する:
\begin{align}
\qquad \frac{2\boldsymbol{\alpha}\cdot\boldsymbol{\beta}}{\boldsymbol{\alpha}^2}=-n_2,
\
\frac{2\boldsymbol{\alpha}\cdot\boldsymbol{\beta}}{\boldsymbol{\beta}^2}=-n_1
\end{align}
またルートに関し、次のようなルールも存在します:
$\boldsymbol{\alpha}$がルートなら$-\boldsymbol{\alpha}$もルート。
$\boldsymbol{\alpha}$がルートなら、$\boldsymbol{\alpha}$のゼロでない倍数(※$-\boldsymbol{\alpha}$は除く)はルートではない。
$\boldsymbol{\alpha},\boldsymbol{\beta}$が異なる正ルートであるとき、$\boldsymbol{\alpha}-\boldsymbol{\beta}$はルートではないことが示せる。
マスター公式
$\boldsymbol{\alpha}$をルート、$\boldsymbol{\mu}$をある表現$D$の任意のウェイトとすると
\begin{align}
\qquad
E_3|\mu,x,D\rangle=\frac{\boldsymbol{\alpha}\cdot\boldsymbol{\mu}}{\boldsymbol{\alpha}^2}|\mu,x,D\rangle
\end{align}
が成立します。$E_3$は上記「SU(2)部分代数」に現れた$E_3$。この$E_3$の固有値に関し、Georgiの教科書Georgiで「マスター公式」と呼ばれている以下の関係が成立します:
\begin{align} \qquad \frac{2\boldsymbol{\alpha}\cdot\boldsymbol{\mu}}{\boldsymbol{\alpha}^2}=q-p \end{align}
ここで$q$は
$\boldsymbol{\mu},\boldsymbol{\mu}-\boldsymbol{\alpha},\boldsymbol{\mu}-2\boldsymbol{\alpha},\cdots,\boldsymbol{\mu}-q\boldsymbol{\alpha}$はルートであるが、$\boldsymbol{\mu}-(q+1)\boldsymbol{\alpha}$はルートではなくなるような整数
$p$は
$\boldsymbol{\mu},\boldsymbol{\mu}+\boldsymbol{\alpha},\boldsymbol{\mu}+2\boldsymbol{\alpha},\cdots,\boldsymbol{\mu}+p\boldsymbol{\alpha}$はルートであるが、$\boldsymbol{\mu}+(p+1)\boldsymbol{\alpha}$はルートではなくなるような整数
です。この公式が以下重要になります。以下$q,p$が現れたときには、この意味での$q,p$であることに注意してください。
最高ウェイト、ディンキン・インデックス, カルタン行列
最高ウェイト$\boldsymbol{\mu}$は、すべての単純ルート$\boldsymbol{\alpha}^i\ (i=1,2,\cdots,r)$に対して$\boldsymbol{\mu}+\boldsymbol{\alpha}^i$がウェイトになり得ないという条件で定義されます。この場合$p=0$でなければならず、マスター公式より各$\boldsymbol{\alpha}^i$に対して
\begin{align}
\qquad
\frac{2\boldsymbol{\alpha}^i\cdot\boldsymbol{\mu}}{(\boldsymbol{\alpha}^i)^2}=q^i
\end{align}
となります。$q^i\ (i=1,2,\cdots,r)$は$0$または正の整数です。単純ルートは一次独立で最高ウェイトに縮退はないから、最高ウェイト$\boldsymbol{\mu}$をもつ既約表現$D$は、$r$個の$0$または正の整数の組$[q^1,q^2,\cdots,q^r]$で完全に指定されます。このリストをディンキン・インデックスと呼びます。さらに$\boldsymbol{\mu}$が最高ウェイトではないウェイトに対しても同様にディンキン・インデックスを定義します。このときディンキン・インデックスは「マスター公式」で示した意味での$q$ではなくなります。このときディンキン・インデックスの各要素は一般に負の整数も取り得ます。また最高ウェイトではない場合、違うウェイト(線形独立なウェイト)が同じディンキン・インデックスを持つこともあります。
ということで改めてディンキン・インデックスを
\begin{align}
\qquad\boldsymbol{\mu}:[l^1,l^2,\cdots,l^r]
\end{align}
ただし
\begin{align}
\qquad
l^i:=\frac{2\boldsymbol{\alpha}^i\cdot\boldsymbol{\mu}}{(\boldsymbol{\alpha}^i)^2}
\end{align}
のように定めます。ディンキン・インデックスの$i$成分は$\boldsymbol{\mu}$の$\boldsymbol{\alpha}^i$に対する$q-p$に対応します(これを$q^i-p^i$と表記します)。
カルタン行列は単純ルート$\boldsymbol{\alpha}^i$に対し、以下で定義されます:
\begin{align} \qquad C_{ji}=\frac{2\boldsymbol{\alpha}^i\cdot\boldsymbol{\alpha}^j}{(\boldsymbol{\alpha}^i)^2} \end{align}
$C$はディンキン図形より構成でき、これが単純ルートからルート系を構成するのに重要です。
基本ウェイト
$j$番目のディンキン・インデックスが$1$で、ほかはすべて0となるような最高ウェイトを$\boldsymbol{\omega}^j$とします。$\boldsymbol{\omega}^j$は各$\boldsymbol{\alpha}^i$に対して
\begin{align}
\qquad \frac{2\boldsymbol{\alpha}^i\cdot\boldsymbol{\omega}^j}{(\boldsymbol{\alpha}^i)^2}=\delta^{ij}
\end{align}
を満たします。もし$\boldsymbol{\alpha}^i$がわかっていれば、この式から$\boldsymbol{\omega}^j$が定まります。$\boldsymbol{\omega}^j$は基本ウェイトと呼ばれます。
一般のディンキン・インデックスに対応する最高ウェイトは、def1の$l^i$に対して
\begin{align}
\qquad \boldsymbol{\mu}=\sum_{i=1}^rl^i\boldsymbol{\omega}^i
\end{align}
で与えられます。$\boldsymbol{\omega}^i$を最高ウェイトとしてもつ$r$個の表現$\rho_i$を基本表現といいます。
上式から、基本ウェイトはカルタン行列$C$を用いて
\begin{align}
\qquad
\boldsymbol{\omega}^i
=\sum_{j=1}^r (C^{-1})_{ji}\boldsymbol{\alpha}^j
\end{align}
で与えられます。
ディンキン図形
上で述べたように、単純リー代数は単純ルートで特徴付けられます。単純ルートを図に表す方法がディンキン図形です。
- ◯は単純ルートを表す
- 2つの単純ルートの相対角度が
- $120^\circ$のとき(すなわち$n_1n_2=1$のとき)対応する2つの単純ルートの◯を1本線でつなぐ
- $135^\circ$のとき(すなわち$n_1n_2=2$のとき)対応する2つの単純ルートの◯を2本線でつなぐ
- $150^\circ$のとき(すなわち$n_1n_2=3$のとき)対応する2つの単純ルートの◯を3本線でつなぐ
- $90^\circ$のとき線ではつながない
- 長さが違う単純ルートを線で結ぶ場合、不等号をつけて長さの大小を表現する(※不等号ではなく矢印かもしれませんが、不等号と理解する方が大小を理解しやすいのでこう言っておきます)
以下にディンキン図形の例を記しておきます。
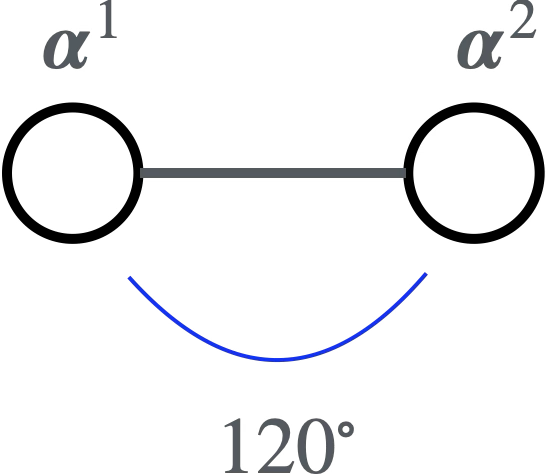 SU(3)
SU(3)
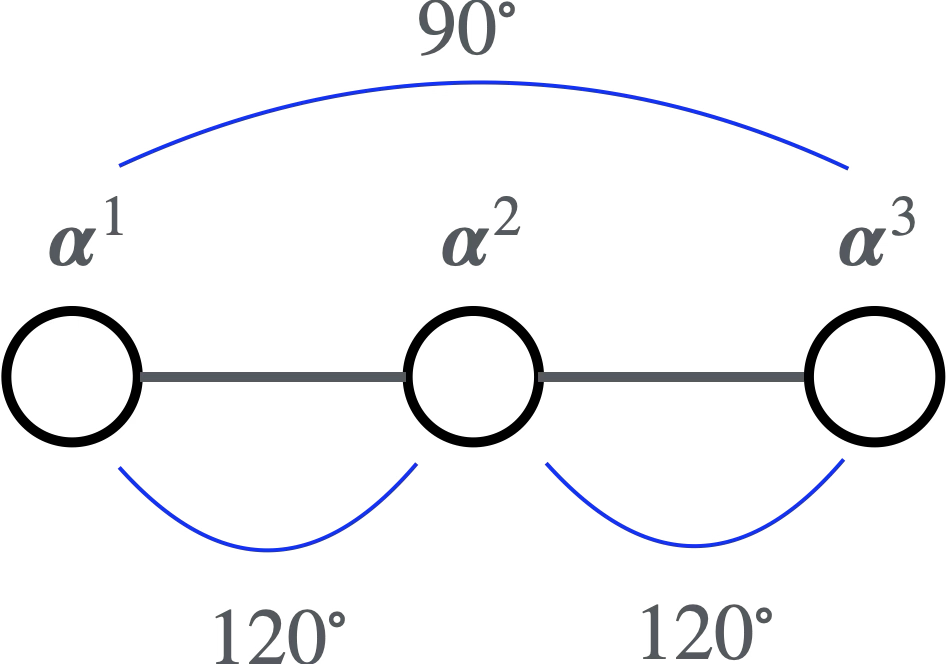 SU(4)
SU(4)
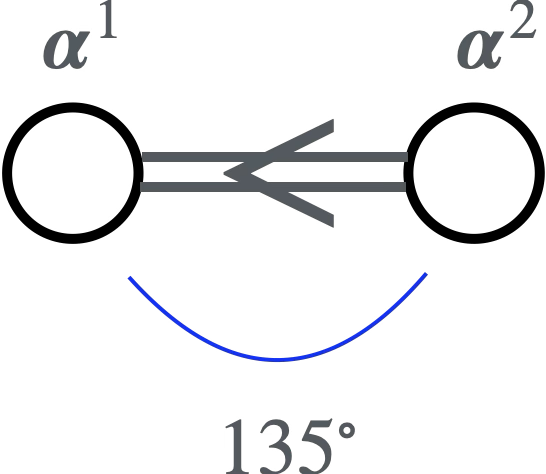 SO(5)
SO(5)
![!FORMULA[115][2029452343][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FNPb9Dvv5zMGXTXxJeADW.png?alt=media) $\rm G_2$
$\rm G_2$
$\boldsymbol{\alpha}^1,\boldsymbol{\alpha}^2,\boldsymbol{\alpha}^3$は単純ルートです。$\rm SO(5),G_2$では$|\boldsymbol{\alpha}^1|<|\boldsymbol{\alpha}^2|$です。またSU(4)で$\boldsymbol{\alpha}^1$と$\boldsymbol{\alpha}^3$の相対角度は$90^\circ$です。一般に線で直接つながれていない単純ルートの間の相対角度は$90^\circ$です。
ちなみに2つの単純ルートの相対角度が$180^\circ$のとき、2つのルートは線形独立ではないので、どちらか1つを採用します。
単純ルートからルート系を構成する
それでは具体的に$\rm G_2$の単純ルートからルート系を構成しましょう。
まず$\rm G_2$のカルタン行列$C$を計算しておきます。ex1の$\rm G_2$のディンキン図形より、2つの単純ルート$\boldsymbol{\alpha}^1,\boldsymbol{\alpha}^2$の相対角度は$150^\circ$ですが、これは$n_1n_2=3$ということです(ディンキン図形の線の本数が$n_1n_2$)。いま$|\boldsymbol{\alpha}^1|<|\boldsymbol{\alpha}^2|$とすれば、fml1の一番下の式より
\begin{align}
\qquad
\frac{2\boldsymbol{\alpha}^1\cdot\boldsymbol{\alpha}^2}{(\boldsymbol{\alpha}^1)^2}=-3, \ \frac{2\boldsymbol{\alpha}^1\cdot\boldsymbol{\alpha}^2}{(\boldsymbol{\alpha}^2)^2}=-1
\end{align}
です。これとdef2にあるカルタン行列の定義より
\begin{align}
\qquad C=
\begin{pmatrix}
2 & -1\\
-3 & 2
\end{pmatrix}
\end{align}
になります(これはGeorgiの$C$といっしょ。Kikkawaではこの転置が$C$)。
1. 逐次的構成
まずは愚直にルート系を構成します。一般に正ルートは$k_i\ (i=1,2,\cdots,r)$を$0$または正の整数の組として
\begin{align}
\qquad\boldsymbol{\alpha}=\sum_{i=1}^rk_i\boldsymbol{\alpha}^i
\end{align}
で書けます。そこで
\begin{align}
\qquad k=\sum_{i=1}^r k_i
\end{align}
として、$k=1$から順に正ルートを構成します。$k$をレベルと呼ぶことにします。$k=l$まで構成できたとして、このレベルのルートを$\boldsymbol{\phi}_l$とします。このとき
\begin{align}
\qquad\boldsymbol{\phi}_l +\boldsymbol{\alpha}^i \ (i=1,2,\cdots, r)
\end{align}
が正ルートになるかどうかを逐次チェックします。$\boldsymbol{\phi}_l+\boldsymbol{\alpha}^i$が正ルートになる条件はマスター公式
\begin{align}
\qquad\frac{2\boldsymbol{\alpha}^i\cdot\boldsymbol{\phi}_l}{(\boldsymbol{\alpha}^i)^2}=q-p
\end{align}
において$p$が$p>0$を満たす整数となることです。$p$がこれを満たすなら、$\boldsymbol{\phi}_{l+1}:=\boldsymbol{\phi}_{l}+\boldsymbol{\alpha}^i$
はレベル$k=l+1$の正ルートになります。
ということで上記のチェックを帰納的に行います:
【$k=1$】
この場合${k_i}$のどれか1つが$1$、あとは$0$であるので、単純ルートそのもの。単純ルートは正ルートなので、この場合 $${ \qquad\boldsymbol{\phi}_1=\boldsymbol{\alpha}^1,\boldsymbol{\alpha}^2}$$ が正ルートとして求まる。【$k=2$】
カルタン行列が
\begin{align} \qquad C= \begin{pmatrix} 2 & -1\\ -3 & 2 \end{pmatrix} \end{align}
であるから$${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{1}\cdot\boldsymbol{\alpha}^{2})}{(\boldsymbol{\alpha}^{1})^2}=-3, \qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{2}\cdot\boldsymbol{\alpha}^{1})}{(\boldsymbol{\alpha}^{2})^2}=-1}$$
である。いま${\boldsymbol{\alpha}^{1},\boldsymbol{\alpha}^{2}}$をそれぞれ${E_{-\boldsymbol{\alpha}^{2}},E_{-\boldsymbol{\alpha}^{1}}}$で落とした状態はルートではないので${q=0}$(※${\boldsymbol{\alpha},\boldsymbol{\beta}}$を単純ルートとすると${\boldsymbol{\alpha}-\boldsymbol{\beta}}$はルートではない)。ゆえにマスター公式よりそれぞれ${p=3,1}$であるからどちらも$p>1$であるため$${\qquad\boldsymbol{\phi}_2:=\boldsymbol{\alpha}^{1}+\boldsymbol{\alpha}^{2}}$$ は正ルート。注
「ルートに関する制限」の章にあるように、$2\boldsymbol{\alpha}^1,2\boldsymbol{\alpha}^2$はルートではないことに注意。
【$k=3$】
- まずは${\boldsymbol{\phi}_2+\boldsymbol{\alpha}^{1}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{1}\cdot\boldsymbol{\phi}_2)}{(\boldsymbol{\alpha}^{1})^2}=-1}$$ また${q=1}$である(∵${\boldsymbol{\boldsymbol{\phi}}_1-\boldsymbol{\alpha}^{1}}$はルートだが、もう一度引くとルートではない)。ゆえに${p=2}$なので $${\qquad \boldsymbol{\phi}_3:=\boldsymbol{\phi}_2+\boldsymbol{\alpha}^{1}=2\boldsymbol{\alpha}^{1}+\boldsymbol{\alpha}^{2}}$$ は正ルート。
- 次に${\phi_2+\boldsymbol{\alpha}^{2}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{2}\cdot\boldsymbol{\phi}_2)}{(\boldsymbol{\alpha}^{2})^2}=-1}$$
また${q=1}$である(∵${\boldsymbol{\phi}_1-\boldsymbol{\alpha}^{2}}$はルートだが、もう一度引くとルートではない)。ゆえに${p=0}$であり${p>0}$を満たさないので ${\boldsymbol{\phi}_2+\boldsymbol{\alpha}^{2}}$ は正ルートではない。
【$k=4$】
- ${\boldsymbol{\phi}_3+\boldsymbol{\alpha}^{1}}$が正ルートか調べる。 $$ {\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{1}\cdot\boldsymbol{\phi}_3)}{(\boldsymbol{\alpha}^{1})^2}=1}$$
また${q=2}$である(∵${\boldsymbol{\phi}_3}$から${\boldsymbol{\alpha}^{1}}$を2回引いてもルートだが、3回引くとルートではなくなる)。ゆえに${p=1}$なので
$${\qquad \boldsymbol{\phi}_4:=\boldsymbol{\phi}_3+\boldsymbol{\alpha}^{1}=3\boldsymbol{\alpha}^{1}+\boldsymbol{\alpha}^{2}}$$
は正ルート。 - 次に${\boldsymbol{\phi}_3+\boldsymbol{\alpha}^{2}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{2}\cdot\boldsymbol{\phi}_3)}{(\boldsymbol{\alpha}^{2})^2}=1}$$
また${q=0}$である(∵${\boldsymbol{\phi}_3}$から${\boldsymbol{\alpha}^{2}}$を引くと${2\boldsymbol{\alpha}^{1}}$となりルートではない)。ゆえに${p=0}$なので${\boldsymbol{\phi}_3+\boldsymbol{\alpha}^{2}}$は正ルートではない。
- ${\boldsymbol{\phi}_3+\boldsymbol{\alpha}^{1}}$が正ルートか調べる。 $$ {\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{1}\cdot\boldsymbol{\phi}_3)}{(\boldsymbol{\alpha}^{1})^2}=1}$$
【${k=5}$】
- ${\boldsymbol{\phi}_4+\boldsymbol{\alpha}^{1}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{1}\cdot\boldsymbol{\phi}_4)}{(\boldsymbol{\alpha}^{1})^2}=3}$$
また${q=3}$である(∵${\boldsymbol{\phi}_3}$から${\boldsymbol{\alpha}^{1}}$を3回引いてもルートだが、4回引くとルートではなくなる)。ゆえに${p=0}$なので${\boldsymbol{\phi}_4+\boldsymbol{\alpha}^{1}}$ は正ルートではない。 - 次に${\boldsymbol{\phi}_4+\boldsymbol{\alpha}^{2}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{2}\cdot\boldsymbol{\phi}_4)}{(\boldsymbol{\alpha}^{2})^2}=-1}$$
また${q=0}$である(∵${\boldsymbol{\phi}_4}$から${\boldsymbol{\alpha}^{2}}$を引くと${3\boldsymbol{\alpha}^{1}}$となりルートではない)。ゆえに${p=1}$なので
$${\qquad \boldsymbol{\phi}_5:=\boldsymbol{\phi}_4+\boldsymbol{\alpha}^{2}=3\boldsymbol{\alpha}^{1}+2\boldsymbol{\alpha}^{2}}$$
は正ルート。
- ${\boldsymbol{\phi}_4+\boldsymbol{\alpha}^{1}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{1}\cdot\boldsymbol{\phi}_4)}{(\boldsymbol{\alpha}^{1})^2}=3}$$
【${k=6}$】
- ${\boldsymbol{\phi}_5+\boldsymbol{\alpha}^{1}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{1}\cdot\boldsymbol{\phi}_4)}{(\boldsymbol{\alpha}^{1})^2}=0}$$
また${q=0}$である(∵${\boldsymbol{\phi}_3}$から${\boldsymbol{\alpha}^{1}}$を引くと${2\boldsymbol{\alpha}^{1}+2\boldsymbol{\alpha}^{2}}$となる。$k=4$のルートは$3\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2$のみなので、これはルートではない)。ゆえに${p=0}$なので${\boldsymbol{\phi}_5+\boldsymbol{\alpha}^{1}}$は正ルートではない。 - 次に${\boldsymbol{\phi}_5+\boldsymbol{\alpha}^{2}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{2}\cdot\boldsymbol{\phi}_4)}{(\boldsymbol{\alpha}^{2})^2}=1}$$
また${q=1}$である(∵${\boldsymbol{\phi}_4}$から${\boldsymbol{\alpha}^{2}}$を引くと${3\boldsymbol{\alpha}^{1}+\boldsymbol{\alpha}^{2}}$となりルート。もういちど${\boldsymbol{\alpha}^{2}}$を引くとルートではなくなる)。ゆえに${p=0}$なので${\boldsymbol{\phi}_5+\boldsymbol{\alpha}^{2}}$は正ルートではない。$_\blacksquare$
- ${\boldsymbol{\phi}_5+\boldsymbol{\alpha}^{1}}$が正ルートか調べる。 $${\qquad\displaystyle\frac{2(\boldsymbol{\alpha}^{1}\cdot\boldsymbol{\phi}_4)}{(\boldsymbol{\alpha}^{1})^2}=0}$$
これをまとめると
\begin{align}
\qquad&\boldsymbol{\alpha}^1,
\boldsymbol{\alpha}^2\\
&\boldsymbol{\alpha}^1+
\boldsymbol{\alpha}^2\\
&2\boldsymbol{\alpha}^1+
\boldsymbol{\alpha}^2\\
&3\boldsymbol{\alpha}^1+
\boldsymbol{\alpha}^2\\
&3\boldsymbol{\alpha}^1+
2\boldsymbol{\alpha}^2
\end{align}
の計6つが正ルート。これらの符号を反転したものが負ルート。合計12個の状態で$\rm G_2$のルート系が構成されます。図にすると以下のようになります。
![!FORMULA[239][2029452343][0]を2次元ユークリッド空間に図示したもの。!FORMULA[240][923716761][0]とした。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F3GKgFraDTsfnDQ0yHwIQ.png?alt=media) $\rm G_2$を2次元ユークリッド空間に図示したもの。$\boldsymbol{\alpha^1}=(0,1), \ |\boldsymbol{\alpha}^1|<|\boldsymbol{\alpha}^2|,\ \boldsymbol{\alpha}^1<\boldsymbol{\alpha}^2$とした。
$\rm G_2$を2次元ユークリッド空間に図示したもの。$\boldsymbol{\alpha^1}=(0,1), \ |\boldsymbol{\alpha}^1|<|\boldsymbol{\alpha}^2|,\ \boldsymbol{\alpha}^1<\boldsymbol{\alpha}^2$とした。
2. ディンキン・インデックスを用いて構成
本章でも1.と同じように単純ルートからルートを構築していくのですが、それらルートをディンキン・インデックスの値でラベルして図示します。
あるウェイト$\boldsymbol{\mu}$がルートであることがわかっているとします。$\boldsymbol{\mu}'$を
\begin{align}
\qquad
\boldsymbol{\mu}'=\boldsymbol{\mu}+\boldsymbol{\alpha}^j
\end{align}
のように$\boldsymbol{\mu}$に$\boldsymbol{\alpha}^j$を足したものだとします。このとき$\boldsymbol{\mu}'$のディンキン・インデックスの$i$成分は
\begin{align}
\qquad
2\frac{\boldsymbol{\alpha}^i\cdot\boldsymbol{\mu}'}{(\boldsymbol{\alpha}^i)^2}=q_{\boldsymbol{\mu}}^i-p_{\boldsymbol{\mu}}^i+C_{ji}=:l_{\boldsymbol{\mu}'}^i,\quad
q^i_{\boldsymbol{\mu}},p^i_{\boldsymbol{\mu}}\text{は}\boldsymbol{\mu}\text{の}q^i,p^i\tag{1}
\end{align}
となり、もとのディンキン・インデックスの$i$成分に$C_{ji}$を足したものになることがわかります。
1.と同様、単純ルートから$\boldsymbol{\alpha}$を足して上のレベルに順次上がっていきます。下から構成する場合「あるウェイトからどの方向にどれだけ連続して下がれるか」の指標である$q$がわかっています。またディンキン・インデックスが計算できるので、マスター公式より$p$を計算することができます。$p$がわかれば「そのウェイトからどの方向にどれだけ連続して上がれるか」がわかります。こうして得られた新たなルートのディンキン・インデックスはEq.(1)で計算できます。これをくりかえしてウェイトのディンキン・インデックスを構成します。ここで$\boldsymbol{\mu}'$は
\begin{align}
\qquad \boldsymbol{\mu}'\leftrightarrow \sum_{i=1}^r l^i_{\boldsymbol{\mu}'} \boldsymbol{\omega}^i
\end{align}
のように基本ウェイトと対応します。
改めてルート系を構築しましょう。
まずは基本ウェイトを計算しておきます。基本ウェイトはランク2の代数の場合、ディンキン・インデックスが$[1,0],[0,1]$の状態に対応します。一般に基本ウェイトはカルタン行列$C$を用いて
\begin{align}
\qquad
\boldsymbol{\omega}^i
=\sum_{j=1}^r (C^{-1})_{ji}\boldsymbol{\alpha}^j
\end{align}
で与えられます。いま
\begin{align}
\qquad
C=
\begin{pmatrix}
2 & -1\\
-3 & 2
\end{pmatrix}
\qquad
\therefore
C^{-1}=
\begin{pmatrix}
2 & 3\\
1 & 2
\end{pmatrix}
\end{align}
なので
\begin{align}
\qquad
\boldsymbol{\omega}^1=2\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2, \
\boldsymbol{\omega}^2=3\boldsymbol{\alpha}^1+2\boldsymbol{\alpha}^2
\end{align}
です。よって$[a,b]$に対応する状態は
\begin{align}
\qquad
[a,b]\leftrightarrow a\boldsymbol{\omega}^1+b\boldsymbol{\omega}^2
=(2a+3b)\boldsymbol{\alpha}^1+(a+2b)\boldsymbol{\alpha}^2
\end{align}
です。
以下Georgiの教科書GeorgiP125に従って議論します。正ルートをディンキン・インデックスを用いて図にしたものを記します:
\begin{alignat*}{6} &k=5&\qquad && &[0,1]& && &&\qquad &3\boldsymbol{\alpha}^1+2\boldsymbol{\alpha}^2 \\ && && &{\tiny (0,1)_q(0,0)_p}& \\ && &\qquad\nearrow& \\ &k=4& &[3,-1]& && && && &3\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2 \\ && &{\tiny (3,0)_q(0,1)_p}& \\ && &\qquad\nwarrow& \\ &k=3& && &[1,0]& && && &2\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2 \\ && && &{\tiny (2,0)_q(1,0)_p}& \\ && && &\qquad\quad\nwarrow& \\ &k=2& && && &[-1,1]& && &\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2 \\ && && && &{\tiny (1,1)_q(2,0)_p}& \\ && && &\qquad\quad\nearrow& &\qquad\;\nwarrow & \\ &k=1& && &[2,-1]& && &[-3,2]& &\boldsymbol{\alpha}^1,\boldsymbol{\alpha}^2 \\ && && &{\tiny (2,0)_q(0,1)_p}& && &{\tiny (0,2)_q(3,0)_p}& \\ && && &\qquad\quad\nwarrow& &\qquad\nearrow& \\ &k=0& && && & [0,0] & && &H_i \end{alignat*}
この図の構成を、$k$が小さい方から説明していきましょう。
- まず$\boldsymbol{\alpha}^1,\boldsymbol{\alpha}^2$に対応する$q-p$
\begin{align} \qquad [2,-1], [-3,2] \end{align}
を$k=1$のレベルに書く。その下に$k=0$のレベルに$[0,0]$(対応する代数で言えばカルタン部分代数$H_i$)を書く。$\boldsymbol{\alpha}^1$を足す作業を左上向き矢印、$\boldsymbol{\alpha}^2$を足す作業を右上向き矢印で表す。これらはex2のダイアグラムの$k=0,1$の部分になる。 - 次のレベル$k=2$に上がるために、$p$を計算する。一般論より$\boldsymbol{\alpha}^i$の$q$は$i$成分のみ$2$で、それ以外はゼロ(∵ルート$\boldsymbol{\alpha}^i$は、$E_{\boldsymbol{\alpha}^i}$と$\boldsymbol{\alpha}^i\cdot H$がなすSU(2)のスピン1表現の最高ウェイト状態。また$j\neq i$のとき$\boldsymbol{\alpha}^i-\boldsymbol{\alpha}^j$はルートではない)。よって$\boldsymbol{\alpha}^1:[2,-1]$に対して$q:(2,0)$、$\boldsymbol{\alpha}^2:[-3,2]$に対して$q:(0,2)$である。これらからマスター公式を用いて$p$を計算すれば$\boldsymbol{\alpha}^1:[2,-1]$に対して$p:(0,1)$、$\boldsymbol{\alpha}^2:[-3,2]$に対して$p:(3,0)$である。ゆえに$[2,-1]$から右上に1回(=$\boldsymbol{\alpha}^2$を1回足す)、$[-3,2]$から左上に3回進める(=$\boldsymbol{\alpha}^1$を3回足す)。$\boldsymbol{\alpha}^i$方向に上がるとき、ディンキン・インデックスはカルタン行列の$i$行ぶんだけ変化する。よって
\begin{align} &\bullet~ k=2: [2-3,-1+2]=[-3+2,2-1]=[-1,1]&&\leftrightarrow \boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2\\ &\bullet~ k=3: [-1+2,1-1]=[1,0]&&\leftrightarrow 2\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2\\ &\bullet~ k=4: [1+2,0-1]=[3,-1]&&\leftrightarrow 3\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2 \end{align}
を得る。 - $[3,-1]$の$p$を計算する。ex2のダイアグラムにあるように$k=4$以下の正ルートはすべて示してある。この図より、$[3,-1]$から連続して下がれる方向は、左下は$0$、右下は$3$である。よって$[3,-1]$の$q$は$q:(0,3)$であり、ゆえに$p:(0,1)$。すなわち右上にひとつ進むことができる。右上に進めば
\begin{align} \bullet~ k=5: [0,1]\leftrightarrow 3\boldsymbol{\alpha}^1+2\boldsymbol{\alpha}^2 \end{align}
を得る。$[0,1]$の$q$はex2のダイアグラムより$q:(0,1)$なので$p:(0,0)$であり、これが最高のルート(随伴表現の最高ウェイト)であることがわかる。$_\blacksquare$
結局やっていることは前章と同じですが、図にするとわかりやすくなります。
3. 随伴表現の最高ウェイトから落として構成
最後に随伴表現のウェイトを構成することで(正)ルートを構成します。2.では下からルートを構成しましたが、今度は上から下に構成していきます。
2.ではすべてのウェイトやルートに対して$q,p$を毎回計算していましたが、それをすることなくディンキン・インデックスの値のみでルート図を構成する方法があります。あるウェイト$\boldsymbol{\mu}$においてディンキン・インデックスの$i$成分が正の整数$l_{\boldsymbol{\mu}}^i$だった場合、$\boldsymbol{\alpha}^i$を用いてそのウェイトから$l^i_{\boldsymbol{\mu}}$回下に進むというルールでウェイトを構成します。この方法はSatoに記載されているため、ここでは「佐藤法」と呼ぶことにします(※一般的な呼び方ではありません)。
$\rm G_2$の随伴表現の最高ウェイトは$[0,1]$である($\boldsymbol{\omega}^1,\boldsymbol{\omega}^2$のうち長い方)ことは既知とします。これから下に進むことにより構成した正ルートの図は以下です:
\begin{array}{cccc} && &\qquad[0,1]& && &3\boldsymbol{\alpha}^1+2\boldsymbol{\alpha}^2 \\ && &\qquad~~~~~~\downarrow {\scriptsize -\boldsymbol{\alpha}^2}& \\ && &\qquad[3,-1]& && &3\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2 \\ && &\qquad~~~~~~\downarrow {\scriptsize -\boldsymbol{\alpha}^1}& \\ && &\qquad[1,0]& && &2\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2 \\ && &\qquad~~~~~~\downarrow{\scriptsize -\boldsymbol{\alpha}^1}& \\ && &\qquad[-1,1]& && &\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2 \\ && &\qquad{\scriptsize -\boldsymbol{\alpha}^1}\swarrow ~\searrow{\scriptsize -\boldsymbol{\alpha}^2}& & \\ && &\quad [-3,2] \qquad [2,-1]& && &\boldsymbol{\alpha}^1, \boldsymbol{\alpha}^2 \\ && &\quad {\scriptsize -\boldsymbol{\alpha}^2}\downarrow \qquad \qquad\downarrow {\scriptsize -\boldsymbol{\alpha}^1}& \\ && &\quad[0,0] \qquad~~~ [0,0]&&& &H_i \end{array}
以下この図の構成法を説明します。
- まず最高ルートである$[0,1]\leftrightarrow 3\boldsymbol{\alpha}^1+2\boldsymbol{\alpha}^2$を一番上に書く。
- ディンキン・インデックスの$i$成分が正の整数だった場合、$\boldsymbol{\alpha}^i$でその正の整数ぶんだけ下に進む。いまの場合2番目の$l$が$1$なので、$\boldsymbol{\alpha}^2$で1つ下に進む。よって$[3,-1]\leftrightarrow 3\boldsymbol{\alpha}^1+\boldsymbol{\alpha}^2$を得る。
- $[3,-1]$は第1成分が3なので$\boldsymbol{\alpha}^1$($\leftrightarrow [2,-1]$)で3回下に進む。すると$[1,0],\ [-1,1],\ [-3,2]$を得る。
- 3.で現れた$[-1,1]$は第2成分が$1$なので、この状態から$\boldsymbol{\alpha}^2$で1回下に進む。進むと$[2,-1]$を得る。
- a. 3.で現れた$[-3,2]$から$\boldsymbol{\alpha}^2$で下に2回進む。1回進めば$[0,0]$を得る。これより下の状態は負ルートであり、正ルートと対称に構成される。
b. 4.で現れた$[2,-1]$から$\boldsymbol{\alpha}^1$で2回下に進む。1回進めば$[0,0]$を得る。これより下の状態は負ルートであり、正ルートと対称に構成される。$_\blacksquare$
このように構成しても、前2章と同じように正ルートが求まります。Appendixで、なぜ佐藤法でルートやウェイトが構成できるかについてコメントします。
ちなみに、前章では$q,p$を計算することで上のレベルに登れるか否かを判断していましたが、たぶんこの章と同じような感じで計算できると思います。すなわち、ex2のダイアグラムでディンキン・インデックスが負の整数となる要素(これを$i$番目の要素とする)を持つ場合、その整数$\times(-1)$だけ$\boldsymbol{\alpha}^i$方向に上に登れるのではないかと思います。それだと$[0,0]$から上に登れないように見えますが、最低ウェイト状態からこのルールで構成すると問題なく最高ウェイトまで登れます。
まとめ
本記事では単純リー代数のうち例外群$\rm G_2$の代数において、3つの方法で単純ルートからルート系全体を具体的に構築しました。覚え書き替わりでした。
おしまい。$_\blacksquare$
$ $
$ $
Appendix 佐藤法はなぜうまくいくか
ここでは佐藤法でルートやウェイトが構築できる理由に関してコメントします。そのために、ここではもうちょっと複雑な$\rm SU(3)$の$\boldsymbol{15}$次元表現のウェイトを構成した図を示します。
![SU(3)の15次元表現。佐藤教科書例4.5の図に!FORMULA[362][36658931][0]を付記した。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fglk0rPB77kDVRskWxgUj.png?alt=media) SU(3)の15次元表現。佐藤教科書例4.5の図に$q,p$を付記した。
SU(3)の15次元表現。佐藤教科書例4.5の図に$q,p$を付記した。
$q,p$を計算してウェイトを構成する方法では、各ウェイトに対してどちらにどれだけ進めるかを付与していくため、正しくウェイトを構成できます。一方佐藤法では、ディンキン・インデックスの$i$成分が正の整数となるとき$\boldsymbol{\alpha}^i$方向にその整数分だけ進めるというルールでウェイトを構成します。ただし、図6左端にある$[-1,1]\to [0,-1]$の部分のように、そこだけ見れば途中で止まるような場合でも、手前の部分でさらに先に進めることがわかっている場合は($[-2,3]$の存在により$-\boldsymbol{\alpha}^2$で3回下に進めることがわかる)先に進むようにします。すると佐藤法は$q,p$を計算する方法と同じウェイト図を再現します。よければex2のダイアグラムでも両者が一致することを確かめてみてください。
佐藤法が正しい結果をもたらす理由をざっくり言うと「分岐点や角で曲がるとき、その曲がる方向のディンキン・インデックスはその方向の$q$に一致する」(これを★とする)からです。
以下ランクは2であるとして議論を進めます。ランクがいくつでも同様の議論ができるかと思います。また$l^i$をディンキン・インデックスの$i$成分とします。
以下図7を基に議論します。★で言う「分岐点」とはあるウェイトから2方向にわかれて1つ下のレベルのウェイトに移る点のことを指します(図7の三角印)。「角」とはあるウェイトから分岐せずに方向を変えて下のレベルのウェイトに移る点のことです(図7の四角印)。
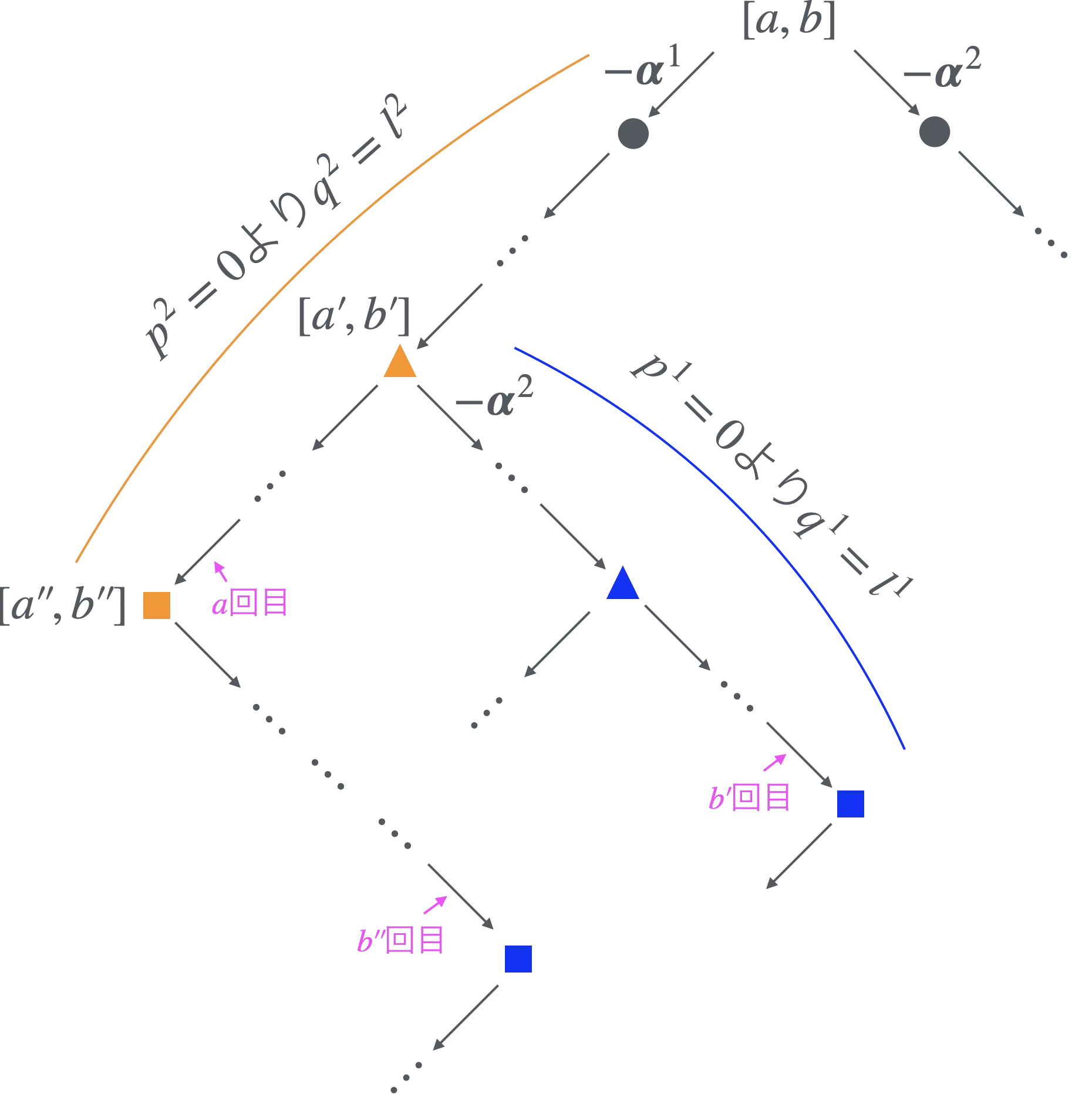 最高ウェイトから下に進みながらウェイトを構成する模式図
最高ウェイトから下に進みながらウェイトを構成する模式図
まず最高ウェイトの$p$が$(0,0)$であることから、最高ウェイトのディンキン・インデックス$l$は$q$に等しいです。そして最高ウェイトから$\boldsymbol{\alpha}^1$方向に進むとき、他の方向に進まぬ限りその経路上のウェイトにおいて$p^2=0$であり、よって$l^2=q^2$となります。ゆえに$l^2$が正の整数になればそこから$\boldsymbol{\alpha}^2$方向に$l^2$だけ進めることがわかります。そして$\boldsymbol{\alpha}^2$方向に1つ以上進むと(他の方向に進まぬ限り)その経路上では$p^1=0$となるので、$l^1$は$q^1$に等しくなります。ゆえに$l^1$が正の整数になればそこから$\boldsymbol{\alpha}^1$方向に$l^1$だけ進めることがわかります。これを繰り返すことになるので、結局★が成立します。ex2のダイアグラムや図6を見ると実際に★が成立していることが確認できます。
ちなみにY,X型の合流点(図8)ではディンキン・インデックスのどの成分も$q$とは対応しなくなりますが、合流前の「上流」にある分岐点や角で既にどこまで進めるかは定まっているので、これが問題になることはないと思います。図6の左端$[-1,1]$はY型の合流点の例ですが、$q$は$(0,2)$であり、どの成分もディンキン・インデックスとは対応していません。しかし上述したように、より上流にある「角」$[-2,3]$の存在により、問題なくウェイトを構成することができます。$_\blacksquare$
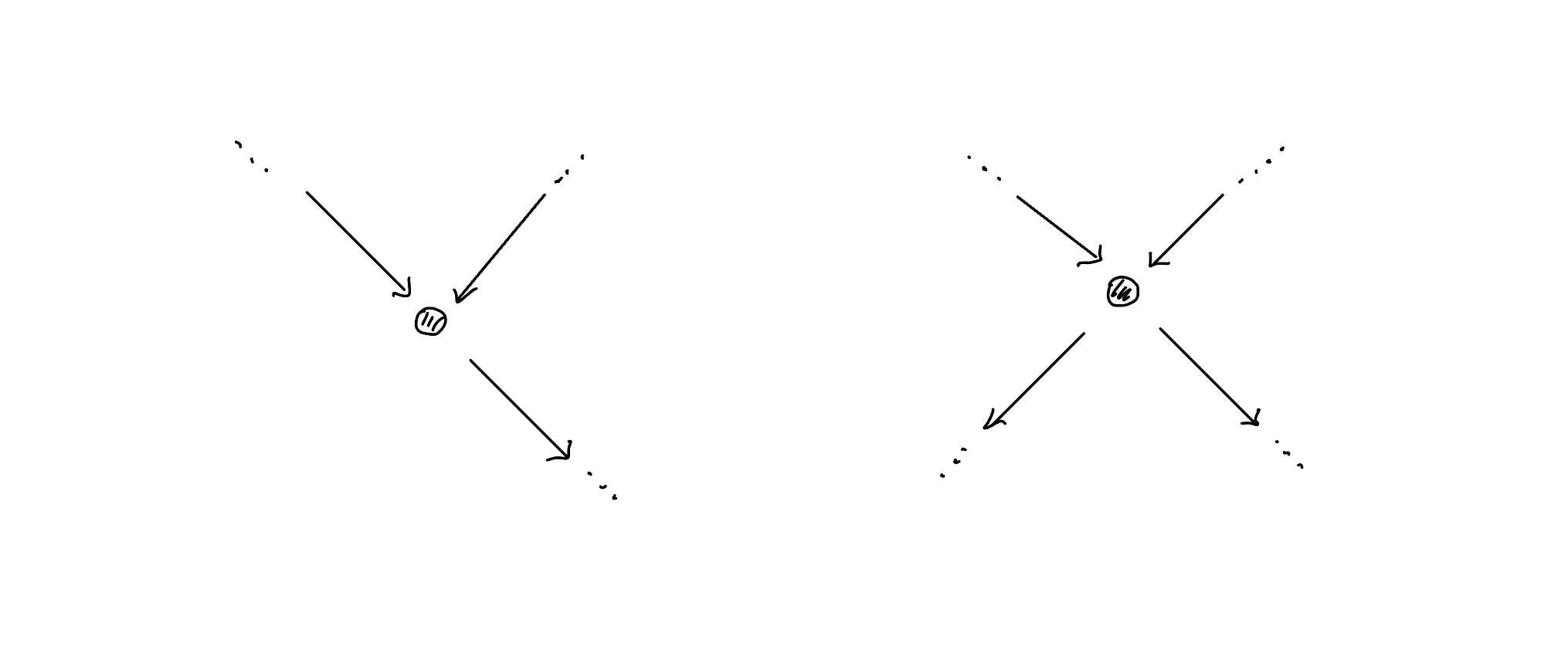 Y,X型の合流点
Y,X型の合流点
