苦手な犬に近づけば遅くなるたかし君が学校に行くまでの最適経路

問題

以下のような，苦手な犬に近づけば近づくほど怯えてしまい，歩く速度が遅くなってしまう少年が家から学校まで行く最適経路を考えましょう．

問題の定式化

$a,b > 0$として，$xy$-平面上に，犬を原点$(0,0)$,家を$(a,0)$，学校を$(-b,0)$に配置して考えましょう．
さらに，たかし君の歩行経路を極座標表示$r = r(\theta)$とします．($r \in C^1 [0,\pi]$を課します．)

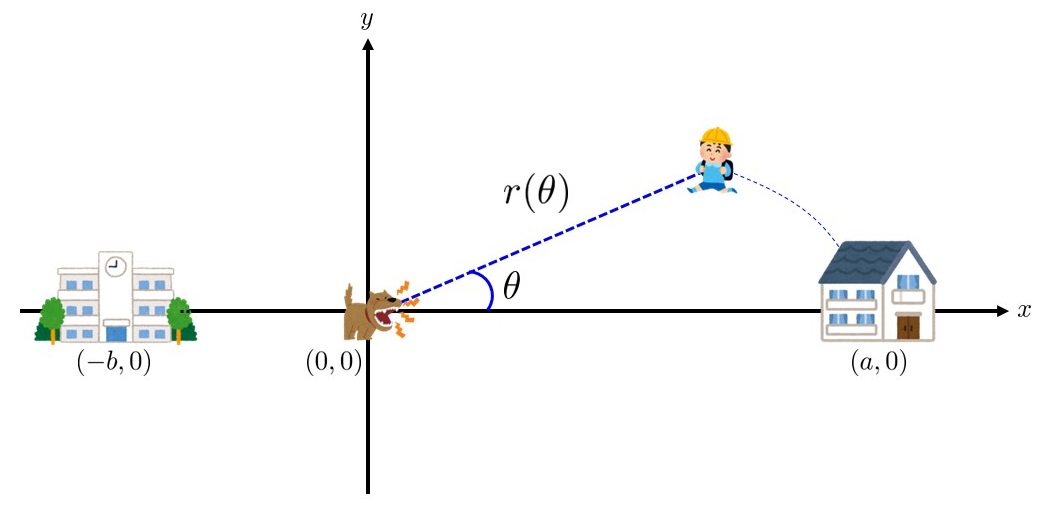
たかし君の速度$v(\theta)$は，犬との距離に比例するため，比例定数$k$として，$v = k r$と書けます．
また，$x = r(\theta) \cos \theta$, $y = r(\theta) \sin \theta$として，たかし君が歩いた微小距離を$d s$とすると，
$\displaystyle ds = \sqrt{\left( \frac{dx}{d \theta} \right)^2 + \left( \frac{dy}{d \theta} \right)^2}~d\theta = \sqrt{r(\theta)^2 + r'(\theta)^2}~d\theta $となります．したがって，たかし君が家から学校まで歩くのにかかる時間は，
\begin{align*} T &= \int_0^{\pi} \frac{ds}{v(\theta)} =\frac{1}{k}\int_0^{\pi} \frac{\sqrt{r(\theta)^2 + r'(\theta)^2}}{r(\theta)} ~ d\theta, \end{align*}
となります．よって，この問題は次のように定式化できます．

解法1 (変分法)

この問題は、関数$r = r(\theta)$が未知で，時間を与える積分を最小化する問題になっています．
このように，インプットが「関数」で，アウトプットが「値」であるような写像を汎関数といい，その最小化問題は変分法を用いて解析することが出来ます．ただし，最小解の存在を個別に示す必要があります．
(後日この変分法および最小解の存在証明(直接法)についての記事を投稿したいと思います．)
ひとまず最小解の存在については認めるものとして議論を進めましょう．
$\displaystyle E(r) := \int_0^{\pi} \frac{\sqrt{r(\theta)^2 + r'(\theta)^2}}{r(\theta)} ~ d\theta$とおくと，
$E$は，ラグランジアン$\displaystyle \mathcal{L}(r',r) = \frac{\sqrt{r^2 + r'^2}}{r}$を持つ汎関数より，
オイラー・ラグランジュ方程式は，定数$C$を用いて，
\begin{align*} &\mathcal{L} - r' \frac{\partial}{\partial r'} \mathcal{L} = C \\ &\Leftrightarrow \frac{\sqrt{r^2 + r'^2}}{r} - \frac{r'^2}{r \sqrt{r^2 + r'^2}} = C \\ &\Leftrightarrow r = C \sqrt{r^2 + r'^2} \\ &\Leftrightarrow C^2 r'^2 = (1 - C^2) r^2, \end{align*}になります．よって，ある定数$A, B$を用いて，$r = A e^{B \theta}$となり，$r(0) = a$, $r(\pi) = b$より，求める経路は
$\displaystyle r = a e^{\frac{1}{\pi} \log (b/a) \theta} = a (b/a)^{\theta/\pi},$
となります．これはいわゆる 対数螺旋と呼ばれる曲線になります．
例えば，$a=1$, $b=2$のとき，以下のような曲線になります．

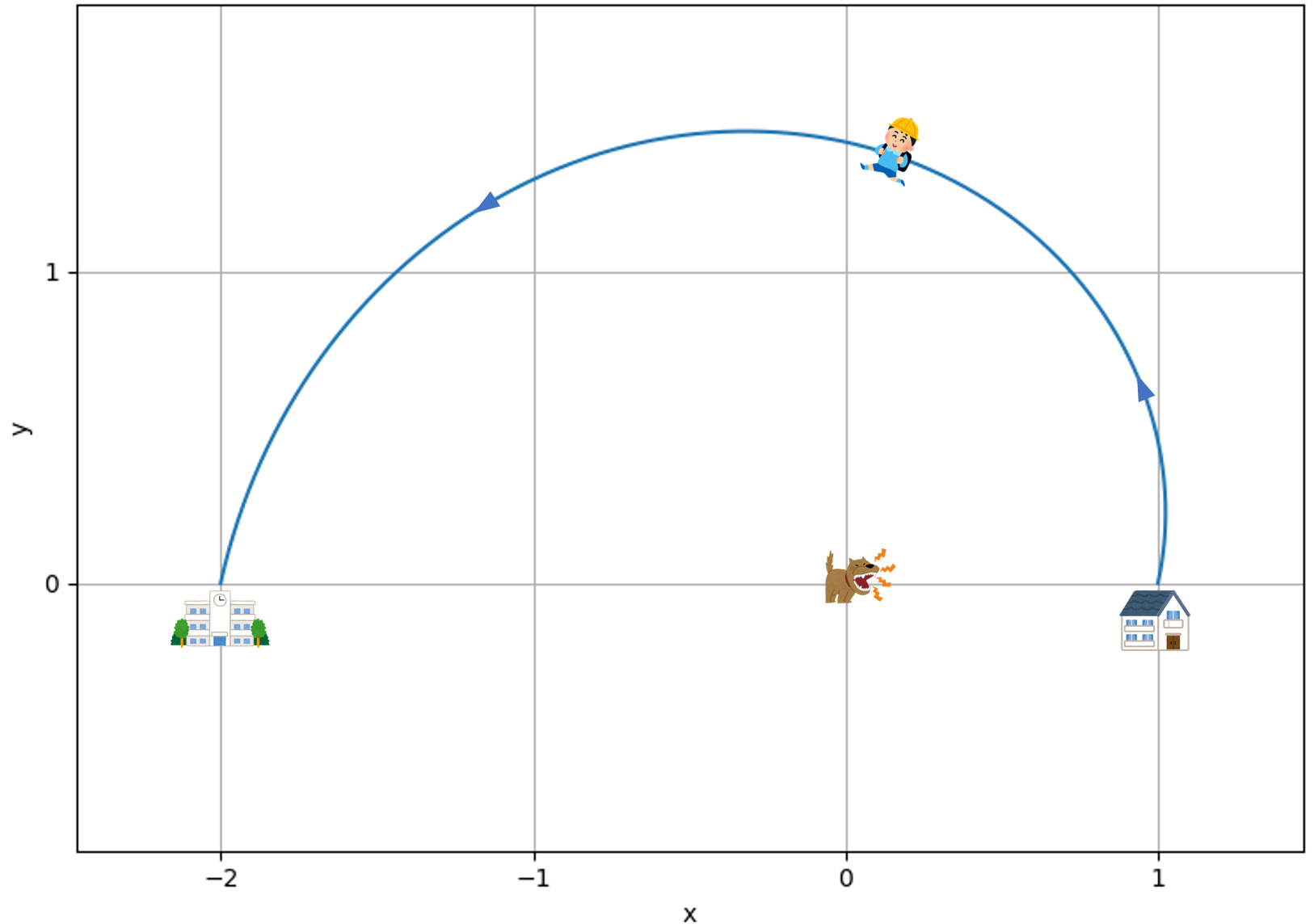
この場合，スタートから少しの間，学校から遠ざかるのは面白いですね．
また，$a = b$，すなわち犬が家と学校の中点にいる場合は経路は半円になります．

対数螺旋は，別名等角螺旋とも呼び，中心から伸ばした半直線と曲線がなす角は一定という性質があります．よって，たかし君は，進行方向と犬がいる方向のなす角度を一定に保って進めば良いことになります．

解法2 (座標変換)

解法1の変分法はより一般的な幅広い問題に対してアプローチ出来る方法ですが，最小解の存在証明はソボレフ空間の議論を用いるなどして少し煩雑というネックがあります．そこでここでは変分法に頼らず解く方法を考えましょう．
汎関数$E$を変形すると，
\begin{align*} \int_0^{\pi} \frac{\sqrt{r(\theta)^2 + r'(\theta)^2}}{r(\theta)} ~ d\theta &= \int_0^{\pi} {\sqrt{1 + \left(\frac{r'(\theta)}{r(\theta)} \right)^2}} ~ d\theta \\ &= \int_0^{\pi} \sqrt{1 + \left(\frac{d}{d\theta}\log r(\theta) \right)^2} ~ d\theta, \end{align*}
となります．したがって，$\infty$を無限遠点，$r = 0$のとき，$(\theta,\log r) := \infty$として，
$xy$-平面からの変換$\psi: \mathbb{R}^2 \to [0,2\pi) \times \mathbb{R} \cup \{\infty \}$を,
$\psi(r \cos \theta , r \sin \theta) := (\theta , \log r)$とすると，
$xy$-平面でのたかし君の点を$\psi$により変換した点$\psi(\mbox{たかし})$は等速に動きます．

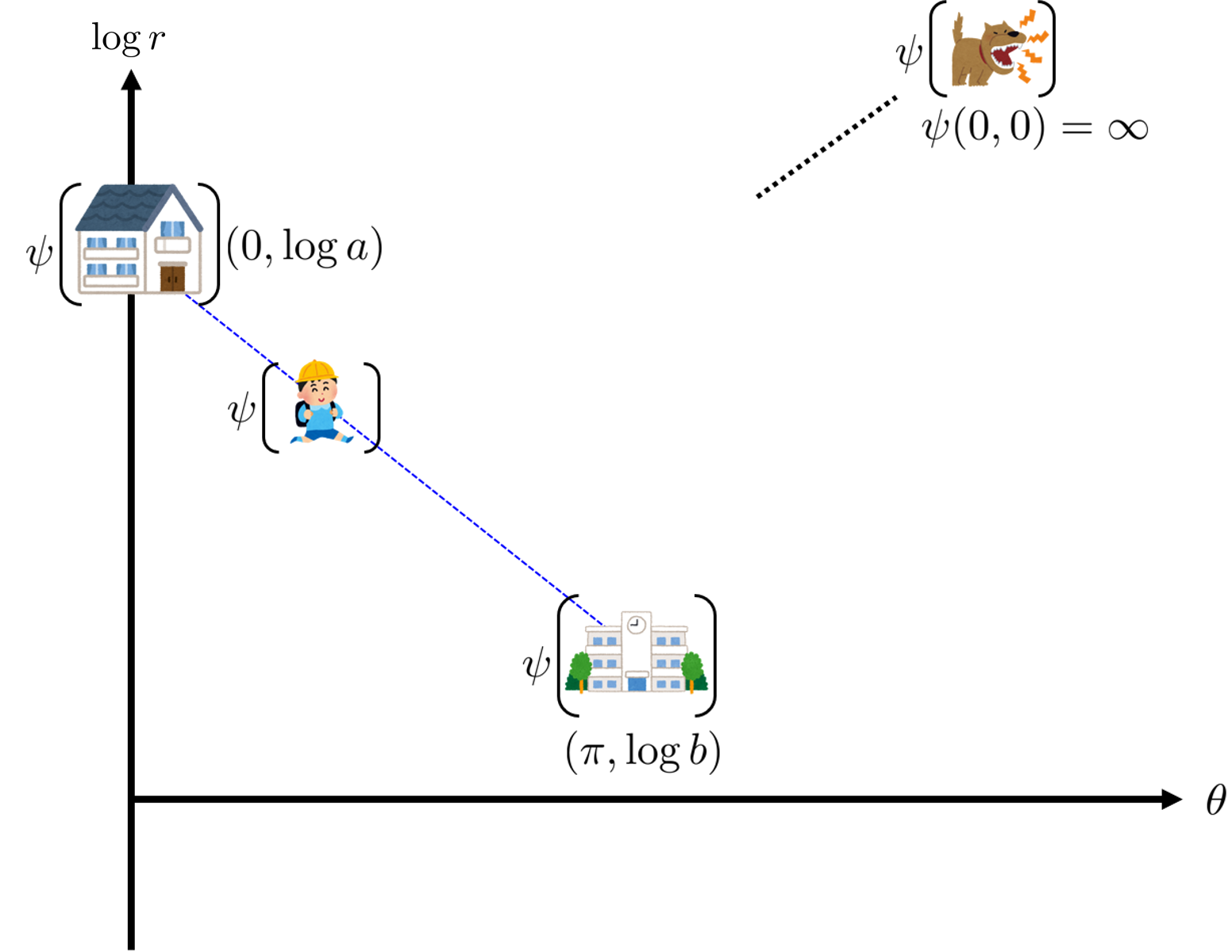
したがってこの問題は，変換後の空間上の点$\psi(\mbox{家})=(0,\log a)$から点$\psi(\mbox{学校}) = (\pi, \log b)$へ等速で動くときの最速経路を求める問題に変換されます．（$\psi(\mbox{犬})$は無限遠点になります．)
もちろんながら，この問題の場合，最速経路は線分になります．
したがって，最速の経路は，$\displaystyle \log r = \frac{1}{\pi} \log(b/a) ~\theta + \log a$となり，解法1で得られた経路と同じになります．