ホモロジー群の計算　精選 100 問

問題

• とくに断りがない場合，$d,m,n$は正整数を表す．
• $S^n,\Delta^n$は$\mathbb{R}^{n+1}$の部分空間
  \begin{align*} S^n&=\{(x_0,x_1,\ldots,x_n)\in\mathbb{R}^{n+1}\mid x_0^2+x_1^2+\cdots+x_n^2=1\},\\ \Delta^n&=\{(x_0,x_1,\ldots,x_n)\in[0,1]^{n+1}\mid x_0+x_1+\cdots+x_n=1\} \end{align*}
  を表す．
• 位相同型，ホモトピー（同倫），線維化 (fibration) などの空間の変形はなるべく具体的に構成すること．
• 空間の単体分割をとる場合，それを具体的に構成する必要はないが，なるべく図示などによって明らかにすること．
• ホモロジー群（同調類群）の生成元をとる場合も，上と同様である．
• 解答を上げる予定はありません．答えを書きたい方はご自由に解説記事を投稿していただければと思います．

$\ $
$\ $
$\ $

$\mathrm{Q. 1}$

内部を含む三角形$X=abc$の整係数ホモロジー群$H_p(X)$ $ (p=0,1,2,\ldots)$の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 2}$

内部を含む三角形$abc$と内部を含まない三角形$ab\cup bd\cup da$があり，点$d$は$abc$の外部にあるとする．和集合$X = abc\cup bd\cup da$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 3}$

点$a\;(=a')$を頂点とし，内部を含まず，自己交差のない一角形$X=aa'$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 4}$

点$a,b\;(=b')$を頂点とし，内部を含まず，自己交差のない二角形$X=ab\cup ab'$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 5}$

$m\geqslant3$とする．内部を含まず，自己交差のない$m$角形
\begin{equation*} X=a_1a_2\cup\cdots\cup a_{m-1}a_m\cup a_ma_1 \end{equation*}
の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 6}$

円環$X=S^1\times[0,1]$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 7}$

内部を含む三角形$abc$において頂点$a, b, c$を同一視した商空間$X = abc / \{a,b,c\}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 8}$

球面$S^2$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 9}$

トーラス$T^2=S^1\times S^1$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 10}$

トーラス$T^2=S^1\times S^1$を
\begin{equation*} (x,(1,0))\sim((1,0),x)\ (x\in S^1) \end{equation*}
で生成される同値関係$\sim$で割った商空間$X=T^2/\mathord{\sim}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 11}$

内部を含む正方形$abcd$において，辺$ab$と辺$cd$をこの向きで貼りあわせた商空間$X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 12}$

内部を含む正方形$abcd$において，辺$ab$と辺$cd$，辺$ad$と辺$bc$をこの向きで貼りあわせた商空間$X$の整係数ホモロジー群の構造を答えよ．また，$X$の$\mathbb{Z}/2\mathbb{Z}$係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 13}$

内部を含む正方形$abcd$において，辺$ab$と辺$cd$，辺$ad$と辺$cb$をこの向きで貼りあわせた商空間$X$の整係数ホモロジー群の構造を答えよ．また，$X$の$\mathbb{Z}/2\mathbb{Z}$係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 14}$

$C\subseteq\mathbb{R}^2\times\{0\}$を$(2,0,0)$を中心とする半径$1$の円周とする．$\mathbb{R}^3$の部分空間$X=C\cup S^2$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 15}$

直線$\mathbb{R}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 16}$

$a,b,p,q$を円周$S^1$上の相異なる$4$点とする．差集合$X=S^1\setminus\{p,q\}$において点$a$と点$b$を同一視した商空間$Y=X/\{a,b\}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 17}$

円周$S^1$において相異なる$m$個の点$a_1,\ldots,a_m$を同一視した商空間$X=S^1/\{a_1,\ldots,a_m\}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 18}$

$\mathbb{R}^3$内の内部を含まない正五角形$ab\cup bc\cup cd\cup de\cup ea$において，対角線$ac,bd,ce,da,eb$を引き，これらをなめらかに変形して互いに交わらないようにした$\mathbb{R}^3$の部分空間$X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 19}$

標準単体$\Delta^n$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 20}$

球面$S^n$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 21}$

$X_1=\cdots=X_m=S^1\times S^1$とする．直和空間$X_1\coprod\cdots\coprod X_m$において，すべての$i\in\{1,\ldots,m-1\}$とすべての$x\in S^1$にたいし，$X_i$の点$(x,(1,0))$と$X_{i+1}$の点$((1,0),x)$を同一視した商空間$X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 22}$

$m\geqslant3$とする．内部を含まない正$m$角形
\begin{equation*} X=a_1a_2\cup\cdots\cup a_{m-1}a_m\cup a_ma_1 \end{equation*}
において，重心$g$と各頂点を結んだ線分の和集合を$Y=a_1g\cup\cdots a_mg$とおく．和集合$X\cup Y$において$X$を$1$点につぶした商空間$Z=(X\cup Y)/X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 23}$

$m\geqslant3$とする．内部を含む正$m$角形$a_1\cdots a_m$において辺$a_1a_2,$ $\ldots,$ $a_{m-1}a_m,$ $a_ma_1$をこの向きで同一視した商空間$X$の整係数ホモロジー群の構造を答えよ．また，すべての素数$p$にたいし，$X$の$\mathbb{Z}/p\mathbb{Z}$係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 24}$

$S^2$において，大円を$m$等分する$m$個の点$a_1,\ldots,a_m$を同一視した商空間$X=S^2/\{a_1,\ldots,a_m\}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 25}$

三角柱$abc\;\text{-}\;def$の側面$X$において$X$の辺$ab,bc,ca$と辺$ef,fd,de$をこの向きでそれぞれ同一視した商空間$Y$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 26}$

内部を含む立方体$abcd\;\text{-}\;efgh$において，面$abcd,$ $abfe,$ $bcgf$と面$hefg,$ $eghd,$ $dhea$をこの順序で頂点が対応するようにそれぞれ貼り合わせた商空間$X$の整係数ホモロジー群の構造を答えよ．また，すべての$p$素数にたいし，$X$の$\mathbb{Z}/p\mathbb{Z}$係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 27}$

閉長方形$X=abcd$において$ab,cd$の中点を$m,n$とし，閉長方形$amnd,bmnc$の内部にそれぞれ開長方形$X_1 = efgh,$ $X_2 = ijkl$が置かれているとする．$X$から$X_1, X_2$の和集合を引いた差集合$Y = X\setminus(X_1 \cup X_2)$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 28}$

$\mathrm{Q. 27}$の$Y$に関して，直積$Y\times[0,1]$の境界
\begin{align*} Z &= (Y\times\{0,1\}) \cup ((ab \cup bc \cup cd \cup da\\ &\qquad {} \cup ef \cup fg \cup gh \cup he\cup ij \cup jk \cup kl \cup li) \times [0,1]) \end{align*}
の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 29}$

$S^1 \times [0,1] \times [0,1]$の境界を
\begin{equation*} X = S^1 \times (([0,1] \times \{0,1\}) \cup (\{0,1\} \times [0,1])) \end{equation*}
とする．直和空間$X\coprod X$において，すべての$x\in S^1 \times [0,1]$にたいし，一方の$X$の点$(x,0)$ともう一方の$X$の点$(x,1)$を同一視した商空間$Y$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 30}$

閉長方形$X = abcd$の内部に開長方形$efgh$が置かれている．辺$ef,gh$の中点を$m,n$とし，開長方形$emnh,fmng$を$X_1,X_2$とおく．また，$X_3 = X \setminus X_1,$ $X_4 = X \setminus X_2$とおき，直積$X_3 \times [0,1],$ $X_4 \times [-1,0]$の境界を
\begin{align*} Y_1&= (X_3 × \{0,1\}) \cup ((ab \cup bc \cup cd \cup da\\ &\qquad\qquad {} \cup em \cup mn \cup nh \cup he) \times [0,1]),\\ Y_2&= (X_4 \times \{-1,0\}) \cup ((ab \cup bc \cup cd \cup da\\ &\qquad\qquad {} \cup fm \cup mn \cup ng \cup gf) \times [-1,0]) \end{align*}
とし，
\begin{equation*} Y_3 = Y_1 \setminus (X_2 \times \{0\}),\quad Y_4 = Y_2 \setminus (X_1 \times \{0\}) \end{equation*}
と定める．和集合$Z=Y_3\cup Y_4$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 31}$

内部を含まない正五芒星とその外接円の和集合$X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 32}$

$\mathbb{R}^n$の部分集合$X$が$\mathbb{R}^n$の星状集合であるとは，ある$a\in X$が存在して，任意の$x\in X$にたいし，$(1-t)a+tx\in X$ $(t\in[0,1])$となることである．$X$を$\mathbb{R}^n$の任意の星状集合とするとき，$X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 33}$

$\mathbb{R}^n$の部分空間$X=\mathbb{R}^n\setminus\{0\}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 34}$

$S^n$から相異なる$m$個の点$a_1,\ldots,a_m$を除いた差集合$X = S^n \setminus \{a_1, \ldots, a_m\}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 35}$

上半空間$X = \mathbb{R}^n \times (0,\infty)$から線分$A = \{0\}^n \times (0,1]$を除いた差集合$Y = X \setminus A$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 36}$

$\mathbb{R}^3$の部分空間$X = \mathbb{R}^3 \setminus (\{0\} \times S^1)$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 37}$

$\mathbb{R}^n$において$a = (1,0,\ldots,0)$と$b = (-1,0,\ldots,0)$を同一視した商空間$X = \mathbb{R}^n / \{a,b\}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 38}$

球面$S^n$を$x\sim-x\ (x\in S^n)$で生成される同値関係$\sim$で割った商空間$\mathbb{R}P^n = S^n/\mathord{\sim}$の整係数ホモロジー群の構造を答えよ．また，すべての素数$p$にたいし，$X$の$\mathbb{Z}/p\mathbb{Z}$係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 39}$

$\mathbb{R}^{n+1}$を
\begin{equation*} (x_0+2,x_1,..,x_n)\sim (-x_0-2,x_1,...,x_n) \end{equation*}
$((x_0,x_1,\ldots,x_n) \in S^n)$で生成される同値関係$\sim$で割った商空間$X = \mathbb{R}^{n+1}/\mathord{\sim}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 40}$

$\mathbb{R}^3=\{(x,y,z)\mid x,y,z\in\mathbb{R}\}$の部分空間$X,Y_1,Y_2,Y_3$を
\begin{align*} X&=\{(x,y,z)\mid \left|x\right|+\left|y\right|+\left|z\right|\leqslant3\},\\ X_1&=\{(x,y,z)\mid \left|x\right|+\left|y\right|<1\},\\ X_2&=\{(x,y,z)\mid \left|y\right|+\left|z\right|<1\},\\ X_3&=\{(x,y,z)\mid \left|z\right|+\left|x\right|<1\} \end{align*}
によって定める．$X$から$X_1,X_2,X_3$の和集合を引いた差集合$Y=X\setminus(X_1\cup X_2\cup X_3)$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 41}$

$(x,y,z)$空間において，$D$を$(3,0,0)$を中心とする半径$1$の開円板で$(x,y)$平面に含まれるものとし，$D$を$y$軸の周りに$1$回転した回転体を$X$とおく．$\mathbb{ R}^3$から$X$を引いた差集合$Y = \mathbb{R}^3 \setminus X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 42}$

$\mathrm{Q. 41}$の$X$を$\mathbb{R}^2 \times [0,\infty)$から引いた差集合$Z = (\mathbb{R}^2 \times [0,\infty)) \setminus X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 43}$

$\mathrm{Q. 41}$の$Y$に関して，$(3,0,0)$を中心とする半径$2$の円周で$(x,y)$平面に含まれるものを$C$とするとき，$Y$を
\begin{equation*} (x,y,z)\sim(-x,-y,-z)\ ((x,y,z) \in C) \end{equation*}
で生成される同値関係$\sim$で割った商空間$W_1 = Y/\mathord{\sim}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 44}$

$\mathrm{Q. 41}$の$Y$に関して，$(0,0,1)$を中心とする半径$1$の円周で平面$z=1$に含まれるものを$C'$とするとき，$Y$を
\begin{equation*} (x,y,z) \approx (-x,-y,-z)\ ((x,y,z) \in C') \end{equation*}
で生成される同値関係$\approx$で割った商空間$W_2 = Y/\mathord{\approx}$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 45}$

内部を含む正十二面体$X$の$1$骨格（すべての辺の和集合）$Y$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 46}$

$n$次元超立方体$X = [0,1]^n$の$(n - 1)$骨格$Y,$　$(n - 2)$骨格$Z,$　$(n - 3)$骨格$W$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 47}$

内部を含まない正四面体$abcd$の$1$骨格において，$ab$と$cd$をこの向きで貼りあわせた商空間$X$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 48}$

$r>0$とする．$\mathbb{R}^3$内の正四面体$abcd$の各頂点を中心とする半径$r$の開球体$B_a,B_b,B_c,B_d$の和集合$X=B_a\cup B_b\cup B_c\cup B_d$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 49}$

すべての$n\in\mathbb{Z}$にたいして，$\mathbb{R}^2$内の点$(n,1/3)$を中心とする半径$1/3$の円周を$C_n$とし，$X = \displaystyle\bigcup_{n\in\mathbb{Z}}^{\vphantom{1}}C_n$とおく．$X$と直線$l=\mathbb{R}\times\{0\}$の和集合$Y=X\cup l$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 50}$

$\mathrm{Q. 49}$の$X$に関して，線分$[-1,1]$との直積を$Z=X\times[-1,1]$とし，同じ線分の境界$\{-1,1\}$との直積を$A=X\times\{-1,1\}$とおく．$Z$において$A$を$1$点につぶした商空間$W=Z/A$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 51}$

トーラス$T^n = (S^1)^n$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 52}$

$\mathbb{R}^2$内の$(1,0)$を中心とする半径$1$の円周を$X_1,$ $\mathbb{R}^4$内の$(0,-1,0,0)$を中心とする半径$1$の$3$次元球面を$X_2$とし，$\mathbb{R}^3$内の$(-1.0,0), (1,0,0)$を中心とする半径$1$の$2$次元球面をそれぞれ$X_3,X_4$とする．$\mathbb{R}^6$の部分空間$X = (X_1 \times X_2) \cup (X_3 \times X_4)$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 53}$

球面$S^n$を$x\sim-x\ (x\in S^n)$で生成される同値関係$\sim$で割った商空間$\mathbb{R}P^n = S^n/\mathord{\sim}$の直積$X=\mathbb{R}P^n\times\mathbb{R}P^n$の整係数ホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 54}$

$\mathbb{R}^2$内の直線$l_1, \ldots, l_m$はどの$3$つも共通部分をもたず，どの$2$つも$1$点で交わるとする．和集合$X = l_1 \cup\cdots\cup l_m$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 55}$

$\mathbb{R}^2$から$\mathrm{Q. 54}$の$X$を引いた差集合$Y=\mathbb{R}^2\setminus X$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 56}$

$\mathbb{R}^3$から直線$l$を引いた差集合$X=\mathbb{R}^3\setminus l$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 57}$

$\mathbb{R}^3$内の直線$l,m$は$1$点で交わるとする．$\mathbb{R}^3$から$l,m$の和集合を引いた差集合$X=\mathbb{R}^3\setminus(l\cup m)$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 58}$

$\mathbb{R}^3$内の内の直線$l, m, n$は共通部分をもたず，どの$2$本も$1$点で交わるとする．このとき，$\mathbb{R}^3$から$l,m,n$の和集合を引いた差集合$X=\mathbb{R}^3\setminus(l\cup m\cup n)$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 59}$

$\mathbb{R}^3$内の平面$H_1, H_2, H_3, H_4$は共通部分をもたず，どの$3$つも$1$点で交わり，どの$2$つも直線で交わるとする．差集合$X=\mathbb{R}^3\setminus(H_1\cup H_2\cup H_3\cup H_4)$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 60}$

平面上に内部を含まない正方形$X_1=ab \cup bc \cup cd \cup da$と，点$a$を中心としてこれを時計回りに$30^\circ$回転させた内部を含まない正方形$X_2=ae \cup ef \cup fg \cup ga$が置かれている．$X_1,X_2$の和集合$X = X_1\cup X_2$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 61}$

$\mathbb{R}^{n+1}$内の点$(0,0,...,0),$ $(1,0,...,0)$を中心とする半径$1$の$n$次元球面$S_1, S_2$の和集合$X=S_1\cup S_2$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 62}$

$\mathbb{R}^{n+1}$内の点$(0,0,...,0),$ $(1,0,...,0),$ $(-1,0,\ldots,0)$を中心とする半径$1$の$n$次元球面$S_1, S_2,S_3$の和集合$X=S_1\cup S_2\cup S_3$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 63}$

$\mathbb{R}^3$内の平面$H$は$S^2$と交わり，その共通部分は円周であるとする．和集合$X=H\cup S^2$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 64}$

$\mathbb{R}^3$において，円柱面$S^1\times\mathbb{R}$と$(0,0,0)$を中心とする半径$2$の$2$次元球面$S$の和集合を$X=(S^1\times\mathbb{R})\cup S$とおく．$X$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 65}$

トーラス$T^2=S^1\times S^1$と球面$S^2$の直和空間を$X=T^2\coprod S^2$とし，
\begin{align*} (x,(1,0)) &\sim \biggl(\frac{\,x\,}{\,2\,}, \frac{\sqrt{3}}{2}\biggr),\\ (x, (-1,0)) &\sim \biggl(\frac{\,x\,}{\,2\,}, -\frac{\sqrt{3}}{2}\biggr)\ (x\in S^1) \end{align*}
で生成される$X$上の同値関係$\sim$を考える．ここで，上式の左辺は$T^2$の元を表し，右辺は$S^2$の元を表す．$X$を$\sim$で割った商空間$Y=X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 66}$

$\mathbb{R}^3$の部分空間$X=(S^1\times\mathbb{R})\cup(\mathbb{R}\times S^1)$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 67}$

$C = S^1$とし，$\mathbb{R}^2$内の$(1,0)$を中心とする半径$1$の円周を$C'$とする．$\mathbb{R}^3$の部分空間$X = (C \times \mathbb{R}) \cup (\mathbb{R} \times C')$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 68}$

$S^2$から$[0,1]$と同相な部分集合$A$を引いた差集合$X = S^2 \setminus A$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 69}$

$S^2$から$S^1$と同相な部分集合$A$を引いた差集合$X = S^2 \setminus A$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 70}$

$m\leqslant n$とする．$S^n$から$[0,1]^m$と同相な部分集合$A$を引いた差集合$X = S^n \setminus A$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 71}$

$m\leqslant n$とする．$S^n$から$S^m$と同相な部分集合$A$を引いた差集合$X = S^n \setminus A$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 72}$

$S^n$を$x\sim-x\ (x \in S^n)$で生成される同値関係$\sim$で割った商空間を$\mathbb{R}P^n = S^n/\mathord{\sim}$とし，$a\in\mathbb{R}P^n$とする．$\mathbb{R}P^n$から$a$を除いた差集合$X = \mathbb{R}P^n \setminus \{a\}$の整係数のホモロジー群の構造を答えよ．

$\ $
$\ $
$\ $

$\mathrm{Q. 73}$

トーラス$T^2=S^1\times S^1$から$1$点$a$を除いた差集合$X = T^2 \setminus \{a\}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 74}$

トーラス$T^2=S^1\times S^1$から$[0,1]$と同相な部分集合$A$を引いた差集合$X = T^2 \setminus A$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 75}$

トーラス$T^2=S^1\times S^1$から$[0,1]^2$と同相な部分集合$A$を引いた差集合$X = T^2 \setminus A$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 76}$

トーラス$T^2=S^1\times S^1$の部分空間
\begin{equation*} X=\{(x,y)\in T^2\mid x\neq y\} \end{equation*}
の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 77}$

トーラス$T^3=S^1\times S^1\times S^1$の部分空間
\begin{equation*} X=\{(x,y,z)\in T^3\mid x\neq y,\ y\neq z,\ z\neq x\} \end{equation*}
の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 78}$

$S^n\times S^n$の部分空間
\begin{equation*} X=\{(x,y)\in S^n\times S^n\mid x\neq y\} \end{equation*}
の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 79}$

正三角形$abc$の重心を$g$とし，$g$と頂点$a,b,c$を結ぶ線分の和集合を$X=ag\cup bg\cup cg$とする．$X\times X$の部分空間
\begin{equation*} X=\{(x,y)\in X\times X\mid x\neq y\} \end{equation*}
の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 80}$

$\mathbb{R}^n\times \mathbb{R}^n$の部分空間
\begin{equation*} X=\{(x,y)\in \mathbb{R}^n\times \mathbb{R}^n\mid x\neq y\} \end{equation*}
の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 81}$

$X = [0,1]^3$を
\begin{equation*} (x,0,0) \sim (x,1,0),\quad(0,x,0) \sim (1,x,0)\ (x \in [0,1]) \end{equation*}
で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 82}$

$X = S^n\times[0,1]$を
\begin{equation*} (x,0) \sim (-x,0)\ (x \in S^n) \end{equation*}
で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 83}$

$X = S^1\times S^1\times[0,1]$を
\begin{equation*} (x,(1,0),0) \sim ((1,0),x,0)\ (x \in S^1) \end{equation*}
で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 84}$

$X = [-1,1]^n\times[0,1]$を
\begin{equation*} (x,0) \sim (-x,1)\ (x \in [-1,1]^n) \end{equation*}
で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 85}$

$X = S^n\times[0,1]$を
\begin{equation*} (x,0) \sim (-x,1)\ (x \in S^n) \end{equation*}
で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 86}$

$X = (S^1)^n\times[0,1]$を
\begin{equation*} (x,0) \sim (-x,1)\ (x \in (S^1)^n) \end{equation*}
で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 87}$

$X = S^1\times[0,1]$を
\begin{equation*} (\cos{mt},\sin{mt}, 0) \sim (\cos{nt},\sin{nt},1)\ (t \in [0,2\pi)) \end{equation*}
で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 88}$

$X = (S^2)^n$を$x\sim-x\ (x\in X)$で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 89}$

$X = S^m\times S^n$を
\begin{equation*} (x,y) \sim (-x,-y)\ (x \in S^m,y\in S^n) \end{equation*}
で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 90}$

$\mathbb{R}^{n+1}$内の$2$点$(1,0,...,0),$ $(-1,0,...,0)$を中心とする半径$2$の$n$次元球面を$S_1, S_2$とし，$X = S_1 \cup S_2$とおく．$X$を$x\sim-x\ (x\in X)$で生成される同値関係$\sim$で割った商空間$Y = X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 91}$

$X=\mathbb{C}^n\setminus\{0\}$とし，$x,y\in X$にたいし，$x=\lambda y$をみたす$\lambda\in\mathbb{C}\setminus\{0\}$が存在するとき，かつそのときに限り，$x\sim y$と定める．商空間$\mathbb{C}P^n=X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 92}$

$\mathbb{R}^3$から正十二面体の$1$骨格$X$を引いた差集合$Y=\mathbb{R}^3\setminus X$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 93}$

$\displaystyle\omega=\frac{-1+\sqrt{-3}}{2}$とおく．$\mathbb{C}^2$の部分空間
\begin{equation*} S=\{(z,w)\in\mathbb{C}^2\mid\left|z\right|^2+\left|w\right|^2=1\} \end{equation*}
を
\begin{equation*} (z,w)\sim(\omega z,\omega^2 w)\ ((z,w)\in S) \end{equation*}
で生成される同値関係$\sim$で割った商空間$X=S/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 94}$

$\mathbb{R}^3$内の曲線
\begin{equation*} c(t) = (t + \sin{\pi t},\ 1 - \cos{\pi t},\ 0)\ (t \in [0,n]) \end{equation*}
の像を$\mathbb{R}^3$から除いた差集合$X = \mathbb{R}^3 \setminus c([0,n])$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 95}$

曲線$c_1, c_2, c_3\;\colon\;\mathbb{R} \rightarrow \mathbb{R}^3$を
\begin{align*} c_1(t) &= (2\cos{t},\ 2\sin{t},\ 0),\\ c_2(t) &= (2 + 2\cos{t},\ 0,\ 2\sin{t}),\\ c_3(t) &= ((2 + \cos{mt})\cos{t},\ (2 + \cos{mt})\sin{t},\ \sin{mt}) \end{align*}
$(t\in\mathbb{R})$によって定める．差集合$X_1 = \mathbb{R}^3 \setminus c_1(\mathbb{R})$を$c_2(t)\sim c_3(t)\ (t \in \mathbb{R})$で生成される同値関係$\sim$で割った商空間$Y_1 = X_1/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．

$\ $
$\ $
$\ $

$\mathrm{Q. 96}$

$\mathrm{Q. 95}$の状況で，曲線$c_4\;\colon\;\mathbb{R} \rightarrow \mathbb{R}^3$を
\begin{align*} c_4(t) &= ((2 + \cos{3t})\cos{2t},\ (2 + \cos{3t})\sin{2t},\ \sin{3t}) \end{align*}
$(t\in\mathbb{R})$によって定める．差集合$X_2 = \mathbb{R}^3 \setminus c_2(\mathbb{R})$を$c_1(t)\approx c_4(t)\ (t \in \mathbb{R})$で生成される同値関係$\approx$で割った商空間$Y_2 = X_2/\mathord{\approx}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 97}$

実$3$次正方行列の全体$M_3(\mathbb{R})$を標準的な方法によって位相空間$\mathbb{R}^9$と同一視する．$M_3(\mathbb{R})$の部分空間
\begin{equation*} X=\{A\in M_3(\mathbb{R})\mid {}^tAA=A{}^tA=E,\ \det{A}=1\} \end{equation*}
の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 98}$

複素$2$次正方行列の全体$M_2(\mathbb{C})$を標準的な方法によって位相空間$\mathbb{C}^4$と同一視する．$M_2(\mathbb{C})$の部分空間
\begin{equation*} X=\{A\in M_2(\mathbb{C})\mid A^{\ast}A=AA^{\ast}=E,\ \det{A}=1\} \end{equation*}
の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 99}$

$(\mathbb{R}^4)^2$の部分空間$X$を
\begin{equation*} X = \{(v,w) \in (\mathbb{R}^4)^2 \mid \{v,w\}\;\text{は線型独立}\} \end{equation*}
によって定め，$X$上の同値関係$\sim$を
\begin{equation*} (v,w) \sim (v',w') \Longleftrightarrow\mathbb{R}v + \mathbb{R}w = \mathbb{R}v' + \mathbb{R}w' \end{equation*}
$((v,w),(v',w') \in X)$によって定める．$X$を$\sim$で割った商空間$Y=X/\mathord{\sim}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $

$\mathrm{Q. 100}$

$(\mathbb{R}^n)^d$の部分空間$X = \{(x_1,...,x_d) \in (\mathbb{R}^n)^d \mid x_i \neq x_j\ (i \neq j)\}$の整係数のホモロジー群の構造を答えよ．
$\ $
$\ $
$\ $
$\ $
$\ $
$\ $

品書き

$\ $

$\text{Q.1 - Q.31}$　単体分割が使えるもの

$\text{Q.32 - Q.40}$　諸公式が使えるもの

$\text{Q.41 - Q.44}$　円形同士が絡んでいるもの

$\text{Q.45 - Q.53}$　骨格，懸垂，直積を求めるもの

$\text{Q.54 - Q.59}$　組みあわせ論様のもの

$\text{Q.60 - Q.67}$　図形が複雑に交わるもの

$\text{Q.68 - Q.75}$　点や線分をくり抜くもの

$\text{Q.76 - Q.80}$　配位空間様のもの

$\text{Q.81 - Q.87}$　上端，下端を貼りあわせるもの

$\text{Q.88 - Q.90}$　対蹠点を貼りあわせるもの

$\text{Q.91 - Q.100}$　寄せ集め
$\ $
$\ $
$\ $
$\ $
$\ $
$\ $

前提知識

ホモロジー群に関する基礎的な事項をまとめる．ここに述べる命題は解答において証明なしに使用してよい．
$\ $
$\ $
$\ $

単体ホモロジー群

$\ $

• 標準単体$\Delta^p.$
  $\ $
• 特異単体$\sigma\;\colon\;\Delta^p\rightarrow X.$
  $\ $
• $\Delta$複体：Hatcher の本 "Algebraic Topology" にある定義で，最後の条件を Hausdorff 性に弱めたもの．
  $\ $
• 単体複体はすべて$\Delta$複体である．
  $\ $
• $\Delta$複体において，頂点を$a_0,a_1,\ldots,a_n$とし，
  \begin{align*} a_i=a_i'=a_i''=\cdots \end{align*}
  とおくことによって，すべての単体を規則的に表記できる．
  $\ $
• 向きづけられた単体の境界：
  \begin{align*} \partial(a_0a_1\cdots a_p)=\sum_{0}^p(-1)^ia_0a_1\cdots\widehat{a_i}\cdots a_p. \end{align*}
  $\ $
• $\Delta$複体$K$のホモロジー群$H_p(K).$
  $\ $
• $K\cong L$（順序同型）ならば，$K,L$は同一の表記法をもち，したがって$H_\bullet(K)\cong H_\bullet(L)$がなりたつ．
  $\ $
• Mayer-Vietoris 完全系列：$K_1,K_2\subseteq K$ならば，
  \begin{align*} 0\longrightarrow C_\bullet(K_1\cap K_2)\longrightarrow C_\bullet(K_1)\oplus C_\bullet(K_2)\longrightarrow C_\bullet(K_1\cup K_2)\longrightarrow 0. \end{align*}
  $2$番目と$3$番目の写像は$x\mapsto(x,x)$および$(y,z)\mapsto z-y$で表される．
  $\ $
• 相対ホモロジー群$H_p(K,L)$と簡約ホモロジー群$\widetilde{H}_p(K).$
  $\ $
• 相対ホモロジー群の完全系列：$L\subseteq K$ならば，
  \begin{align*} 0\longrightarrow C_\bullet(L)\longrightarrow C_\bullet(K)\longrightarrow \frac{C_\bullet(K)}{C_\bullet(L)}\longrightarrow 0. \end{align*}
  $2$番目と$3$番目の写像は包含写像，商写像である．
  $\ $
• 骨格の相対ホモロジー群：
  \begin{align*} H_p\bigl(K^{\leqslant q},K^{\leqslant q-1}\bigr)\cong\begin{cases} C_q(K)&(p=q)\\ 0&(p\neq q). \end{cases} \end{align*}
  $\ $
• 切除定理：$K_1,K_2\subseteq K$ならば，$H_\bullet(K_1\cup K_2,K_2)\cong H_\bullet(K_1,K_1\cap K_2).$
  $\ $
• 相対ホモロジー群の Mayer-Vietoris 完全系列：$K_1,K_2,L_1,L_2\subseteq K$かつ$L_1\subseteq K_1,$ $L_2\subseteq K_2$ならば，Mayer-Vietoris 完全系列から誘導される完全系列
  \begin{align*} 0\longrightarrow \frac{C_\bullet(K_1\cap K_2)}{C_\bullet(L_1\cap L_2)}\longrightarrow \frac{C_\bullet(K_1)\oplus C_\bullet(K_2)}{C_\bullet(L_1)\oplus C_\bullet(L_2)}\longrightarrow \frac{C_\bullet(K_1\cup K_2)}{C_\bullet(L_1\cup L_2)}\longrightarrow 0 \end{align*}
  が存在する．
  $\ $
• すべての可微分多様体は$\Delta$複体の構造をもつ．
  $\ $
  $\ $
  $\ $

特異ホモロジー群

$\ $

• 位相空間$X$の特異ホモロジー群$H_p(X).$
  $\ $
• Mayer-Vietoris 完全系列：$A,B\subseteq X$であり，$X=A^\circ\cup B^\circ$ならば，
  \begin{align*} 0\longrightarrow C_\bullet(A\cap B)\longrightarrow C_\bullet(A)\oplus C_\bullet(B)\longrightarrow C_\bullet(X)\longrightarrow 0. \end{align*}
  $2$番目と$3$番目の写像は$x\mapsto(x,x)$および$(y,z)\mapsto z-y$で表される．
  $\ $
• 相対ホモロジー群$H_p(X,A)$と簡約ホモロジー群$\widetilde{H}_p(X).$
  $\ $
• 相対ホモロジー群の完全系列：$A\subseteq X$ならば，
  \begin{align*} 0\longrightarrow C_\bullet(A)\longrightarrow C_\bullet(X)\longrightarrow \frac{C_\bullet(X)}{C_\bullet(A)}\longrightarrow 0. \end{align*}
  $2$番目と$3$番目の写像は包含写像，商写像である．
  $\ $
• 切除定理：$\overline{B}\subseteq A\subseteq X$ならば，$H_\bullet(X,A)\cong H_\bullet(X\setminus B,A\setminus B).$
  また，この同型は包含写像$(X\setminus B,A\setminus B)\rightarrow(X,A)$によって誘導される．
  $\ $
• 相対ホモロジー群と商空間：$A\subseteq X$の開近傍で，$A$に変位縮退する (deformation retracts) ものが存在するならば，$H_\bullet(X,A)\cong \widetilde{H}_\bullet(X/A).$
  また，この同型は商写像$X\rightarrow X/A$によって誘導される．
  $\ $
• 相対ホモロジー群の Mayer-Vietoris 完全系列：$A,B,C,D,Y\subseteq X$かつ$C\subseteq A,$ $D\subseteq B$であり，$X=A^\circ\cup B^\circ$かつ$Y=C\cup D=C^\circ\cup D^\circ$ならば，Mayer-Vietoris 完全系列から誘導される完全系列
  \begin{align*} 0\longrightarrow \frac{C_\bullet(A\cap B)}{C_\bullet(C\cap D)}\longrightarrow \frac{C_\bullet(A)\oplus C_\bullet(B)}{C_\bullet(C)\oplus C_\bullet(D)}\longrightarrow \frac{C_\bullet(X)}{C_\bullet(Y)}\longrightarrow 0 \end{align*}
  が存在する．
  $\ $
• $\Delta$複体$K$の単体ホモロジー群$H_\bullet(K)$と，$K$の定める多面体の特異ホモロジー群$H_\bullet(\left|K\right|)$は同型である．
  $\ $
  $\ $
  $\ $

ホモロジー群の性質

$\ $

• $X\simeq Y$（ホモトピー同値）ならば，$H_\bullet(X)\cong H_\bullet(Y).$
  $\ $
• 懸垂同型：$\widetilde{H}_{p+1}(\Sigma X)\cong\widetilde{H}_p(X).$
  $\ $
• 普遍係数定理：係数環を$\mathbb{Z}$から$M$に変えるとき，
  \begin{align*} H_p(X;M)\cong H_p(X)\otimes M\mathrel{\oplus}\mathrm{Tor}^1(H_{p-1}(X),M). \end{align*}
  $\ $
• Künneth の公式：
  \begin{align*} H_p(X\times Y)\cong\bigoplus_{p=q+r}H_q(X;H_r(Y)). \end{align*}
  $\ $
• Serre 線維化 (fibration) $F\rightarrow E\rightarrow B.$
  $\ $
• Leray-Serre スペクトル系列：
  \begin{align*} E^2_{q,r}=H_q(B;H_r(F))\Longrightarrow H_{q+r}(E). \end{align*}
  $\ $
  $\ $
  $\ $

図式と系列

$\ $

• 可換図式
  $\ $
• 短完全系列の解法：短完全系列$0\rightarrow L\rightarrow M\rightarrow N\rightarrow 0$において$N$が有限生成かつ自由ならば，$M\cong L\oplus N.$
  $\ $
• 長完全系列の解法：長完全系列$(C_\bullet,\partial_\bullet)$と$p\in\mathbb{Z}$にたいし，$C_\bullet$の一部分
  \begin{align*} C_{p+2}\xrightarrow{\partial_{p+2}}C_{p+1}\longrightarrow C_p\longrightarrow C_{p-1}\xrightarrow{\partial_{p-1}}C_{p-2} \end{align*}
  から誘導される短完全系列
  \begin{align*} 0\longrightarrow\mathop{\mathrm{Coker}}{\partial_{p+2}}\longrightarrow C_p\longrightarrow \mathop{\mathrm{Ker}}{\partial_{p-1}}\longrightarrow0 \end{align*}
  が存在する．
  $\ $
• 五項補題
  $\ $
• 鎖複体の簡約：相対ホモロジー群の完全系列を用いると，ホモロジー群の構造を保ちながら，鎖複体をより簡単な鎖複体に変形できる．これにより，$\Delta$複体のホモロジー群の計算における単体の数を減らすことができ，$\mathrm{CW}$複体による分割と同程度の分量の計算に帰着できる場合がある．
  $\ $
• ホモロジー長完全系列：鎖複体$(C_\bullet,\partial_\bullet),$ $(C'_\bullet,\partial'_\bullet),$ $(C''_\bullet,\partial''_\bullet)$からなる任意の完全系列
  \begin{align*} 0\longrightarrow C_\bullet\xrightarrow{\ \ f_\bullet\ \ } C'_\bullet\xrightarrow{\ \ g_\bullet\ \ } C''_\bullet\longrightarrow0 \end{align*}
  にたいし，鎖複体からなるつぎの完全対が存在する．ここで，$H_\bullet(f_\bullet),H_\bullet(g_\bullet)$は次数$0$であり，$\overline{\partial}_\bullet$は次数$-1$である．
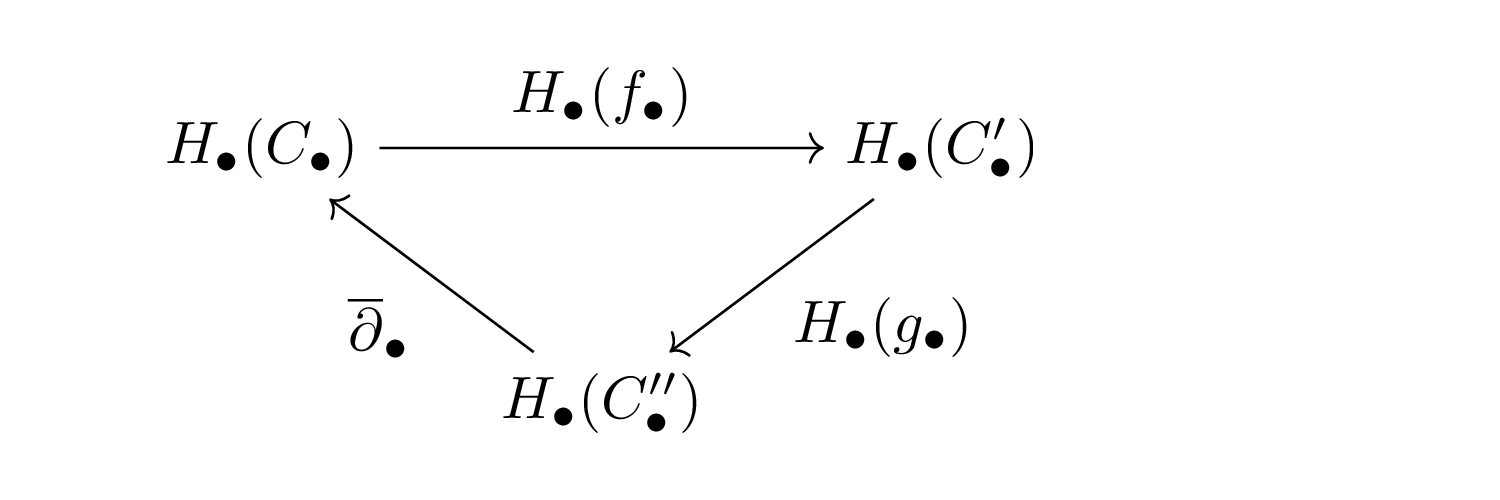  完全対
  さらに，つぎの可換図式をみたす次数$-1$の鎖準同型$\overline{\partial}_\bullet\;\colon\;C''_\bullet\rightarrow C_\bullet$が存在し，これが上記の完全対の次数つき鎖準同型$\overline{\partial}_\bullet$を誘導する．
  次数つき鎖準同型$\overline{\partial}_\bullet$
  $\ $
• 整数成分からなる行列の行簡約および列簡約
  $\ $
• 有限生成アーベル群の構造定理
  $\ $
• テンソル積：係数環を$R$として，
  \begin{align*} M\otimes R&\cong R\otimes M\cong M,\\ L\otimes(M\oplus N)&\cong L\otimes M\oplus L\otimes N,\\ M\otimes N&\cong N\otimes M. \end{align*}
  また，係数環が$\mathbb{Z}$のとき，非負整数$m,n$と整数$a,b$にたいして，
  \begin{align*} \mathbb{Z}^m\otimes\mathbb{Z}^n\cong\mathbb{Z}^{mn},\quad\frac{\mathbb{Z}}{a\mathbb{Z}}\otimes\frac{\mathbb{Z}}{b\mathbb{Z}}\cong\frac{\mathbb{Z}}{\gcd(a,b)\mathbb{Z}}. \end{align*}
  $\ $
• ねじれ函手：
  \begin{align*} \mathrm{Tor}^1(M_1\oplus M_2,N)&\cong\mathrm{Tor}^1(M_1,N)\oplus\mathrm{Tor}^1(M_2,N),\\ \mathrm{Tor}^1(M,N_1\oplus N_2)&\cong\mathrm{Tor}^1(M,N_1)\oplus\mathrm{Tor}^1(M,N_2). \end{align*}

また，$M$または$N$が自由ならば，$\mathrm{Tor}^1(M,N)=0.$

さらに，係数環が$\mathbb{Z}$のとき，正整数$a,b$にたいして，
\begin{align*} \mathrm{Tor}^1(\mathbb{Z},\mathbb{Z})&=0,\\ \mathrm{Tor}^1\Bigl(\frac{\mathbb{Z}}{a\mathbb{Z}},\mathbb{Z}\Bigr)&=0,\\ \mathrm{Tor}^1\Bigl(\mathbb{Z},\frac{\mathbb{Z}}{b\mathbb{Z}}\Bigr)&=0,\\ \mathrm{Tor}^1\Bigl(\frac{\mathbb{Z}}{a\mathbb{Z}},\frac{\mathbb{Z}}{b\mathbb{Z}}\Bigr)&\cong\frac{\mathbb{Z}}{\gcd(a,b)\mathbb{Z}}.\\ \end{align*}
$\ $
$\ $
$\ $
$\ $
$\ $
$\ $