テンソルネットワークで紡ぐ宇宙 ~1.イジング模型からはじめよう~
 君のお気に入りはいたかな?
君のお気に入りはいたかな?
この記事はPhysics Labアドベントカレンダー9日目の記事です。
ダイアグラムに魅せられて
みなさんはじめまして。Hiroと言います。
突然ですが皆さん、ダイアグラムは好きですか?
ダイアグラムというのは言葉や文章だけでは分かりにくい情報や関係性を、図形や線、記号などを用いて視覚的に表現・整理・抽象化した図のことです。例えば電車の路線図だったり、会社や部活の組織図だったり、人間の社会にはダイアグラムで書かれたものがたくさんあります。そのおかげで僕たちは一目見ただけでパッと中身を理解して、自分の欲しい情報をゲットすることができますね!
 東京都の地下鉄の路線図。もし全部文章だったら乗り換え地獄...
東京都の地下鉄の路線図。もし全部文章だったら乗り換え地獄...
 スポーツの作戦ボードなんかもある種のダイアグラムかも?
スポーツの作戦ボードなんかもある種のダイアグラムかも?
僕は物理を専攻している学生なわけですが、物理学では様々な条件や仮定、計算を行った結果として一見すると訳のわからない数式が現れることがたくさんあります。例えば下の式は熱力学ポテンシャルを導く式の一部なのですが、一見すると何がどうなっているのか訳がわかりません。
$\begin{equation}
\frac{1}{8}\sum_{\alpha_1\cdots\alpha_8} \int_0^\beta d\tau_1 \int_0^\beta d\tau_2 V_{\alpha_1\alpha_2\alpha_3\alpha_4} V_{\alpha_5\alpha_6\alpha_7\alpha_8} G^0_{\alpha_1}(\tau_2-\tau_1)\delta_{\alpha_1,\alpha_7}G^0_{\alpha_2}(-\eta)\delta_{\alpha_2,\alpha_4}G^0_{\alpha_6}(-\eta)\delta_{\alpha_6,\alpha_8}G^0_{\alpha_3}(\tau_2-\tau_1)\delta_{\alpha_3,\alpha_5}
\end{equation}$僕は計算が大嫌いなのでこのような計算を直接やるのはできるだけやりたくありません。そもそも数式上では計算ができても実際に何が起こってるのか分からなければ物理としては意味がないでしょう。ですが、じつば物理学には便利な方法があって、さっきの式を下のようなお絵かきで表してあげることができます。
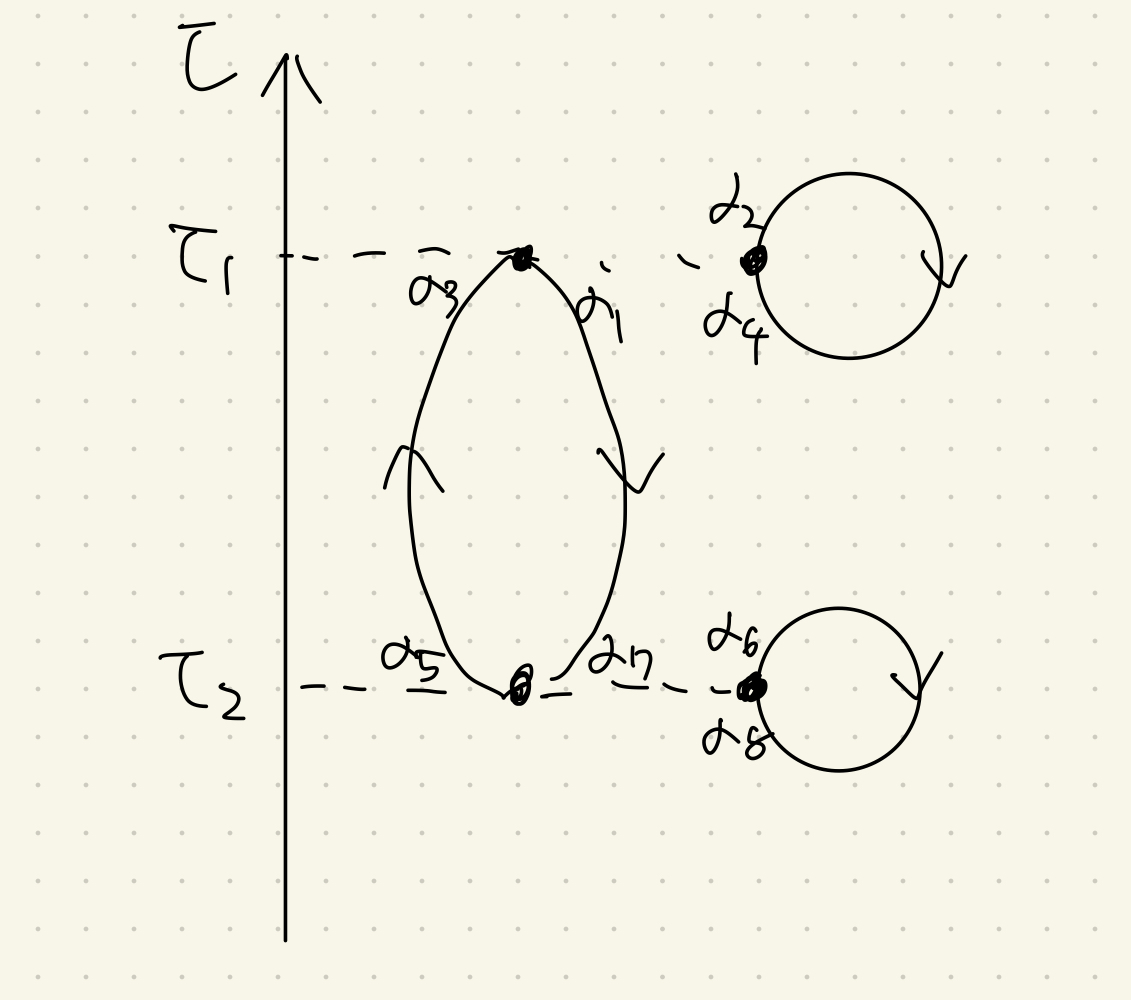 凝縮系における場の量子論(田島裕之)より引用
凝縮系における場の量子論(田島裕之)より引用
これが有名なファインマンダイアグラムと呼ばれるものです。さっきのよくわからない積分計算が一変、このような綺麗な描像に纏まりました。結局最後は適当な条件の上で計算をしないといけなかったりするのですが、本質的な情報だけを抜き取り、一目で構造が理解できるものにするという営みには、物理学の理念に通じる、とてつもなく大きな価値があると感じています。
今回から3回のシリーズで扱っていくテンソルネットワークもこのようなダイアグラムの一種です。物理学における数多くの概念は線形代数の枠組みで書くことができ(もしくは近似的に線形だとみなせ)ます。たくさんの値を持った高次元の行列を、その自由度の数に注目することで、たくさんのブロックの合体でお絵かきするのがテンソルネットワークです。これだけでは単なる便利な計算手法だと思われるかもしれませんが、3回のシリーズを通じてその構造そのものから、奥深い理論物理の問いに迫っていこうと思います。
諸分野の初等的な内容については前提としてあまり解説しない予定です。どうぞよろしくお願いします。
 よろしくね!
よろしくね!
まずはイジング模型から
イジング模型
まずは今回の話の土台となる1次元の古典イジング模型について考えていきましょう。今回はスタンダードな$N$サイトのイジング模型として以下のようなハミルトニアンを考えます。
$\begin{equation} H = -h \sum_{i} s_i - J \sum_{\langle i,j \rangle} s_i s_j \end{equation}$
ここで$\langle i,j \rangle$は最近接サイトのペアを表します。このハミルトニアンにはそれぞれのスピンの向きだけで決まる項と、隣同士のスピンの相互作用で決まる項がありますね。
例えば2つのサイト$i$と$j$のスピンが同じ方向を向いていれば第一項$-J$、反対方向を向いていれば$+J$という値を取ります。また、今回は周期境界条件$s_{N+1}=s_1$
ハミルトニアンが与えられた物理系で、様々な物理量の計算をしたいとなったら、まずは分配関数$Z$を計算することが筋でしょう。今回の場合分配関数$Z$は各スピンの取りうる値について和を取った
$\begin{equation}
Z = \sum_{s_1,s_2,\dots,s_N} e^{-\beta H}
\end{equation}$
となります。もう一度さっきの式をみてみると、変数が$s_1\cdots s_N$の$N$個でこれらがそれぞれ$\pm 1$をとるので全部でパターンは$2^N$個あることがわかります。
これを愚直に計算するのはあまりに大変なので、代わりに転送行列と呼ばれる手法を使って計算していきます。この転送行列が、今後の話のキーポイントになっていきます。
転送行列
今回全てのサイトで重みづけは等しくなっています。ここで磁場に対する応答の項$h \sum_{i} s_i$を、隣接するサイト$(i,i+1)$に分配できるように変形してみましょう。
\begin{equation}
h \sum_{i} s_i = \frac{h}{2} \sum_{i} (s_i + s_{i+1})
\end{equation}
となります。このようにすると、両方の項が隣接するサイト$(i,i+1)$におけるスピンの値で書けるようになります。そこでこの局所的なハミルトニアンに注目すると、
\begin{equation}\label{eq:local_hamiltonian}
H_i = -\frac{h}{2} (s_i + s_{i+1}) - J s_i s_{i+1}
\end{equation}
となります。ここのスピン$s_i,s_{i+1}$の値がそれぞれ$\pm 1$をとるので、このハミルトニアンは4通りの値を取り、それらを$2\times 2$行列の形で表すことができます。ここでは分配関数を計算することを考えて、$e^{-\beta H_i}$を行列の形で表すと、
\begin{equation}
A_i = \begin{pmatrix}
A_i^{1,1}& A_i^{1,-1} \\
A_i^{-1,1}& A_i^{-1,-1} \\
\end{pmatrix}
=\begin{pmatrix}
e^{\beta (h + J)} & e^{-\beta J} \\
e^{-\beta J} & e^{\beta (-h + J)}
\end{pmatrix}
\end{equation}
となります。ここで$A_i$の肩についている添字は$s_i,s_{i+1}$の値を表してます。このような行列の表示を転送行列と呼びます。この転送行列を使うと、分配関数は
\begin{equation}
Z = Tr [A_1 A_2 \cdots A_N]
\end{equation}
となるのです。
これがなぜうまくいくのかは少し考えると簡単にわかります。$A_i$と$A_{i+1}$はスピン$s_{i+1}$を共有しているので、その値については
同じになる必要があります。そこで$A_i$と$A_{i+1}$の積を考えると、
\begin{equation}
A_i A_{i+1} = \begin{pmatrix}
A_i^{1,1} A_{i+1}^{1,1} + A_i^{1,-1} A_{i+1}^{-1,1} & A_i^{1,1} A_{i+1}^{1,-1} + A_i^{1,-1} A_{i+1}^{-1,-1} \\
A_i^{-1,1} A_{i+1}^{1,1} + A_i^{-1,-1} A_{i+1}^{-1,1} & A_i^{-1,1} A_{i+1}^{1,-1} + A_i^{-1,-1} A_{i+1}^{-1,-1} \\
\end{pmatrix}
\end{equation}
となります。これをみると行列の積は、各部分で共通するスピン自由度に関して縮約をとった形になっていることがわかりますね。
これらを$s_i,s_{i+2}$の値で再度インデックス付けすれば同じような転送行列になるので、繰り返し計算していっても同じような計算が現れることがわかります。最後に、今周期境界条件を課しているので、全て掛け合わせた後では一番最初と一番最後のスピンの値が同じになる必要がありますね。これは上の行列をみればトレースを取る操作に対応しているというわけです。これで分配関数を全てのスピン自由度を見る代わりにたった2つの値のみを見れば良くなりました!
具体的に計算するときには、対角化が役に立ちます。転送行列$A_i$を対角化すると、
\begin{equation}
A_i = U_i \Lambda_i U_i^{-1}
\end{equation}
と対角化することを考えると、固有値行列$\Lambda_i$は、
\begin{equation}
\begin{split}
\Lambda_i &= \begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2 \\
\end{pmatrix}\\
&=\begin{pmatrix}
e^{\beta J}\cosh(\beta h)+\sqrt{e^{2\beta J}\sinh^2(\beta h)+e^{-2\beta J}} & 0 \\
0 & e^{\beta J}\cosh(\beta h)-\sqrt{e^{2\beta J}\sinh^2(\beta h)+e^{-2\beta J}} \\
\end{pmatrix}
\end{split}
\end{equation}
となります。トレースは対角化しても変わらないことを思い出せば
\begin{equation}
Z = Tr [A_1 A_2 \cdots A_N] = Tr [\Lambda_1 \Lambda_2 \cdots \Lambda_N]=\sum_{i=1,2} \lambda_i^N
\end{equation}
となります。これを計算すると
\begin{equation}
Z = \left(e^{\beta J}\cosh(\beta h)+\sqrt{e^{2\beta J}\sinh^2(\beta h)+e^{-2\beta J}}\right)^N + \left(e^{\beta J}\cosh(\beta h)-\sqrt{e^{2\beta J}\sinh^2(\beta h)+e^{-2\beta J}}\right)^N
\end{equation}
とできました。このように転送行列を使うことで、分配関数を簡単に計算することができましたね。
転送行列のビジュアライズ
この転送行列は一体何をしていたのでしょうか?それを知るために転送行列をダイアグラムで書き下してみましょう。
行列やテンソルををオブジェクトとして扱い、その添え字をオブジェクトから出た足として表現する。
また足同士がつながった2つのオブジェクトについては、対応する添え字について縮約をとったものと考える。つまり
$\sum_{s_2}A_{s_1,s_2}B_{s_2,s_3}$
のような計算を行う。
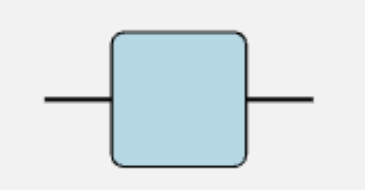 自由度が2つの行列のダイアグラム
自由度が2つの行列のダイアグラム
このような記法を使うと先程の分配関数は、足が2本の転送行列の積になるので、ダイアグラムでは
 イジング模型のダイアグラム表記
イジング模型のダイアグラム表記
となります。
これによって先程の式$Z=Tr[A_1 A_2 \cdots A_N]$の図形的表現を得ることができました。今回の嬉しかったポイントをまとめると
- 最初$2^N$個もあったパターンを4パターンの行列の積に分解できた。
- これによって分配関数を単なる累乗の計算で行うことができた。
- さらに大きなテンソルを小さなテンソルの繋ぎ合わせで書くことができた。
このような巨大自由度のテンソルを小さなテンソルに分解することこそが、テンソルネットワークの理念です。あまりに身近なイジング模型の転送行列が今回の話のプロローグを飾ってくれました。次節ではさらに大きなテンソルを扱うべく、その次元は空間、時間方向に伸びていきます。
量子・古典対応
2次元イジング模型
テンソルネットワークの一般論を考えるにあたっては、より高次のテンソルを考えたくなります。そのためのトイモデルとして先程の1次元イジング模型を2次元に拡張したものを考えてみましょう。ただ、磁場の項は不必要に計算が複雑になるので、今後は使わずにいきましょう。
2次元正方格子上のイジング模型は
\begin{equation}
H = -J \sum_{\langle i_1,j_1 \rangle,\langle i_2,j_2 \rangle} \sigma_{i_1,i_2} \sigma_{j_2,j_2}
\end{equation}
となります。ここで$\sigma_{i_1,i_2}$はサイト$(i_1,i_2)$のスピンを表し、$\langle i_1,j_1 \rangle,\langle i_2,j_2 \rangle$は隣接するサイトを表します。
このようなハミルトニアンを先程同様局所的なハミルトニアンに分解することを考えるのですが、ここでは小さな正方形を作るような4サイトに注目しようと思います。
これら4サイトのスピンを下図に従って$s_{i_1,i_2},s_{i_1-1,i_2},\sigma_{i_1,i_2},\sigma_{i_1,i_2-1}$と名付けます。
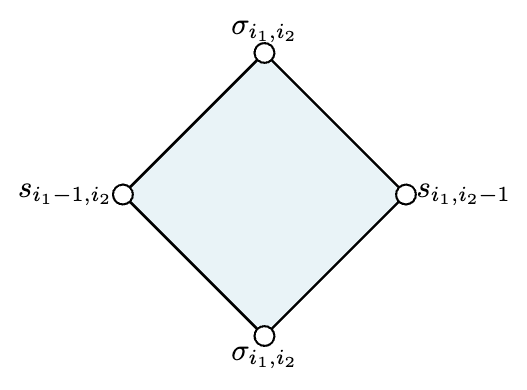 4頂点に注目!
4頂点に注目!
このように名付けたスピンを使って、ハミルトニアンを書き下すと
\begin{equation}
H = -J \left(\sigma_{i_1,i_2} s_{i_1-1,i_2} + \sigma_{i_1,i_2} s_{i_1,i_2} + s_{i_1-1,i_2} \sigma_{i_1,i_2-1} + s_{i_1-1,i_2} \sigma_{i_1,i_2} \right)
\end{equation}
となります。
さっきは$s_i,s_{i+1}$のみを考えていたので、添え字2つのテンソルでした。
しかし今回は$s_{i_1,i_2},s_{i_1-1,i_2},\sigma_{i_1,i_2},\sigma_{i_1,i_2-1}$の4つを考えているので、4つ足のテンソルになります。
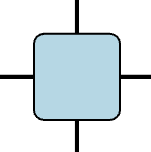 また会ったね!
また会ったね!
これを使って分配関数を計算すると次のような複雑な図形になります。
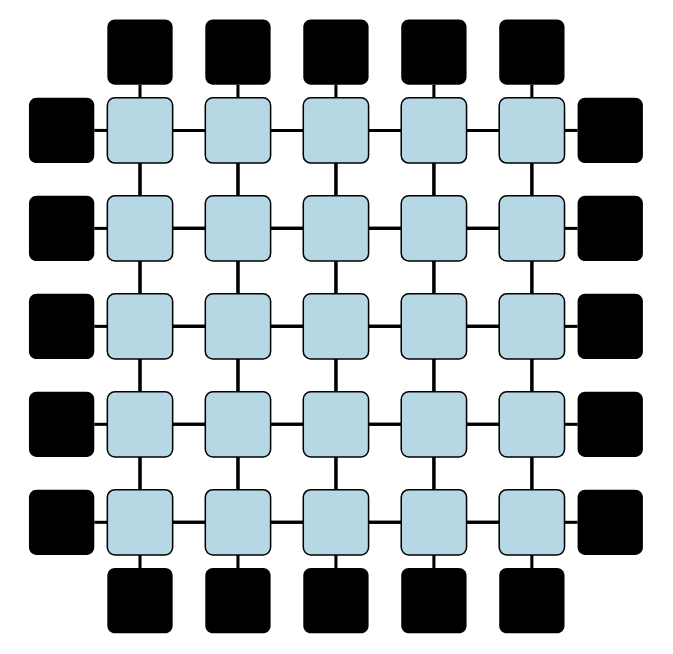 びっくりさせてごめんなさい...
びっくりさせてごめんなさい...
ここで黒い正方形は境界条件を考えており、端っこのサイトのスピンの自由度を持っています。先ほどは周期境界条件があったので、反対側と繋がって閉じていましたね。このような系の分配関数を、下側から計算していくことを考えましょう。
まず各転送行列を4つの足を持つ$W_{i,j}=W\begin{pmatrix} &\sigma_{i,j} & \\ s_{i-1,j} & &s_{i,j}\\&\sigma_{i,j-1}& \end{pmatrix}$と書くことにしましょう。このようにすると、隣同士のテンソルの行列としての積、つまり1変数で縮約を取ると、
\begin{equation}
\begin{split}
\sum_{s_{i,j}}W_{i,j} W_{i+1,j} &= \sum_{s_{i,j}}W\begin{pmatrix} &\sigma_{i,j} & \\ s_{i-1,j} & &s_{i,j}\\&\sigma_{i,j-1}& \end{pmatrix}W\begin{pmatrix} &\sigma_{i+1,j} & \\ s_{i,j} & &s_{i+1,j}\\&\sigma_{i+1,j-1}& \end{pmatrix} \\
&= X\begin{pmatrix} &\sigma_{i,j} &&\sigma_{i+1,j}& \\ s_{i-1,j} & &&&s_{i+1,j}& \\&\sigma_{i,j-1}& &\sigma_{i+1,j-1}& \end{pmatrix}
\end{split}
\end{equation}
と、足が6つにのテンソルになります。
これを元にして、各列のテンソルについて先に全て積を取ってしまうと、
\begin{equation}
T_{j}=T\begin{pmatrix} &\sigma_{1,j} &\sigma_{2,j}& \cdots & \sigma_{N,j}& \\ & & & \cdots & \\&\sigma_{1,j-1}& \sigma_{2,j-1}& \cdots & \sigma_{N,j-1}& \end{pmatrix}
\end{equation}
となります。これを一つのテンソルだと思ってしまえば、あとは1次元系の時と同じような状態であることがわかりますね
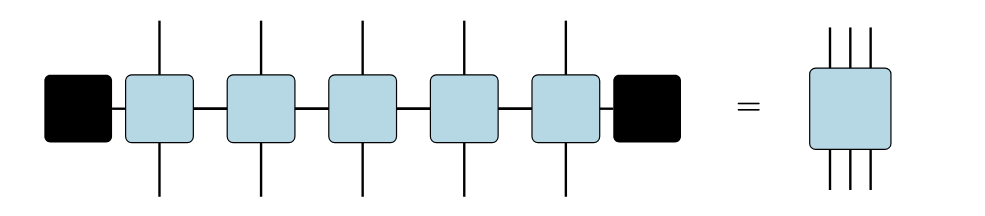 転送行列
転送行列
これが2次元イジング模型における転送行列になります。これによって2次元系でも自由度を局所的に消しながら分配関数の計算にこぎつけることができました。
今この転送行列による分配関数は、一番下の境界条件を$|\Phi_0\rangle$、一番上の境界条件を$|\Phi_N\rangle$とすれば、ブラケットの記法を用いて
\begin{equation}
Z = \langle \Phi_0 | T_1 T_2 \cdots T_N | \Phi_N \rangle
\end{equation}
と書くことができます。この式は内部で結合しているスピンに関して自然に縮約を取った形になっています。
このようにしておけば、たとえば$\sigma_{i,j}$のスピンの期待値は
\begin{equation}
\langle \sigma_{i,j} \rangle = \frac{1}{Z} \langle \Phi_0 | T_1 T_2 \cdots T_j (\sigma_z)_{i,j} T_{j+1} T_{j+2} \cdots T_N | \Phi_N \rangle
\end{equation}
となります。あとは1次元の時と同様に、固有値分解を行って期待値を計算することができます。今回の場合は磁場の項がないので、有限系では自明に0ですが...
MPSとMPO
今回の転送行列の計算では、横方向でのテンソルの計算に注目し、それを縦に重ねていくという考え方を使いました。ここで一段目までのテンソル$T_1|\Phi_0\rangle$を考えてみましょう。
すると、この図形は3つのパーツに分解することができます。
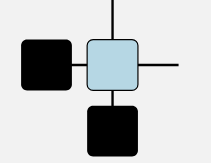 左側
左側
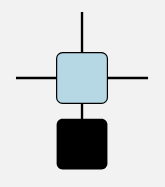 真ん中
真ん中
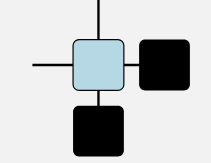 右側
右側
これらの要素はそれぞれ隣同士の要素とスピン$s_{i-1,1},s_{i,1}$の値を共有しています。そのため、上向きに出ている$\sigma_{i,1}$を外向きの自由度と考えれば、このダイアグラムは
内部自由度$s_{i,1}$で縮約をとった、$N$階のテンソルとみなすことができます。これをMPS(Matrix Product State)と呼びます。
同様に転送行列$T_2$に注目すると、これはMPSを引数として受け取り、MPSを返す演算子とみなすことが出来ます。これをMPO(Matrix Product Operator)と呼びます。
古典から量子への接続
さて、だんだんとダイアグラムの見方に慣れてきましたでしょうか?今までの話では古典系を扱って、テンソルネットワークを導入してきました。では量子系でも同じようなダイアグラムによる表記は可能なのでしょうか?
ここでは1次元の量子系として横磁場イジング模型を考え、これがどのように古典系と結びつくかを考えていきましょう。
横磁場イジング模型のハミルトニアンは次のようになります。
\begin{equation}
H = -h \sum_{i} \sigma_i^x - J \sum_{\langle i,j \rangle} \sigma_i^z \sigma_j^z
\end{equation}
ここで$\sigma_i^x,\sigma_i^z$は$i$番目のサイトにおける$x$成分と$z$成分のパウリ行列を表します。
まずはこの模型の基底状態での物理的描像を見てみましょう。たとえば$h\gg J$の極限では、各サイトのスピンは$\sigma_x=+1$の方向を向いていることがわかります。
一方で$h\ll J$の極限では、各サイトのスピンは$\sigma_z=\pm 1$の方向を全員が向いていることがわかります。
このような性質を鑑みると、$h\ll J$では自発的にスピンが揃う強磁性的な性質、$h\gg J$ではスピンが磁場なしでは揃わない常磁性的な性質を持つことがわかります。でも今回はスピンは連続値、さっきのように単純な足しあわせで分配関数を求めることはできません。
ここではまったく別のアプローチとしてこの状態の基底状態を求めることを考えてみましょう。量子ハミルトニアンが与えられた時に、その基底状態を求める有用な手法として、虚時間発展法があります。
適当に用意した初期状態$|\Psi(0)\rangle$に対して、通常の時間発展演算子$e^{-iHt}$(特に明記していませんが、自然単位系で考えています。)の代わりに、虚時間発展演算子$e^{-H\tau}$を用いて、
\begin{equation}
|\Psi(\tau)\rangle = e^{-H\tau} |\Psi(0)\rangle
\end{equation}
という形で時間発展を行うことを考えます。このようにすると、虚時間$\tau$が大きくなるにつれて、基底状態に近づくことが期待されます。
しかしながら、$N$サイトに及ぶハミルトニアンを全てパウリ行列で展開して、一発で$e^{-H\tau}$を求めるというのはあまりにも現実的ではありません。
そこで虚時間発展演算子を小さなステップに分割した上で、鈴木・トロッター分解と呼ばれる手法を用いて展開してみよう。
まずはハミルトニアンを古典系の時のように局所ハミルトニアンの形にしましょう。
\begin{equation}
h_i = -\frac{h}{2} (\sigma_i^x + \sigma_{i+1}^x) - J \sigma_i^z \sigma_{i+1}^z
\end{equation}
これを、作用する基底を$z$方向で場合分けした$|\uparrow_i,\uparrow_{i+1}\rangle,|\uparrow_i,\downarrow_{i+1}\rangle,|\downarrow_i,\uparrow_{i+1}\rangle,|\downarrow_i,\downarrow_{i+1}\rangle$で展開すると、
\begin{equation}
\begin{pmatrix}
-J & -h/2 & -h/2 & 0 \\
-h/2 & J & 0& -h/2 \\
-h/2 & 0 & J & -h/2 \\
0 & -h/2 & -h/2 & -J \\
\end{pmatrix}
\end{equation}
ここで$\sigma_x$が$z$基底表示でスピンを上下入れ替えることを用いました。これはある種2変数をとる転送行列のようになっていることがわかると思います。
次にこれを$e$の肩に乗せることを考えるのですが、その際に$\tau=M\Delta\tau$として、微小虚時間$\Delta\tau$での時間発展の繰り返しと考えることにしましょう。
すると、ここで鈴木・トロッター分解(今回紹介するものは厳密にはトロッター分解と呼ばれることが多く、鈴木トロッター分解と言った時には$e^{-H\tau} \simeq (e^{-H_e\tau/2} e^{-H_o\tau} e^{-H_e\tau/2})^M$の形のものを指すことが多い。こちらの方が漸近的には精度が高い。)を用いることが出来ます。
局所ハミルトニアン$\{h_i\}_{i=1}^N$の和として書けるハミルトニアン$H$に対して、
偶数番目の局所ハミルトニアンのみの和を$H_e$、奇数番目の局所ハミルトニアンのみの和を$H_o$とした時、
\begin{equation}
e^{-H\tau} \simeq (e^{-H_e\Delta\tau} e^{-H_o\Delta\tau})^M+\mathcal{O}(\Delta\tau)
\end{equation}
となる。
これを用いることで$e^{-h_i\Delta\tau}\simeq 1-h_i\Delta\tau$を計算することができます。
\begin{equation}
e^{-h_i\Delta\tau} \simeq \begin{pmatrix}
1+J\Delta\tau & h/2\Delta\tau & h/2\Delta\tau & 0 \\
h/2\Delta\tau & 1-J\Delta\tau & 0 & h/2\Delta\tau \\
h/2\Delta\tau & 0 & 1-J\Delta\tau & h/2\Delta\tau \\
0 & h/2\Delta\tau & h/2\Delta\tau & 1+J\Delta\tau \\
\end{pmatrix}
\end{equation}
これが$i$が偶数のものと奇数のものを繰り返し繰り返し計算することで、$e^{-H\tau}$を計算することができます。
この$4\times 4$行列にみなさん見覚えはありませんか?2次元の古典イジング模型のテンソルネットワークを考えた時に同じような4本足のテンソルが出てきました。今回の場合とのアナロジーを見るために、今計算した行列をダイアグラムで表すと、
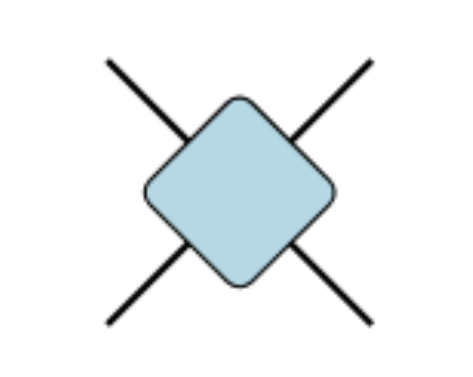 局所ハミルトニアンの図
局所ハミルトニアンの図
これが偶数サイトと奇数サイトで交互に繰り返していくので、全体像は次のようになります。
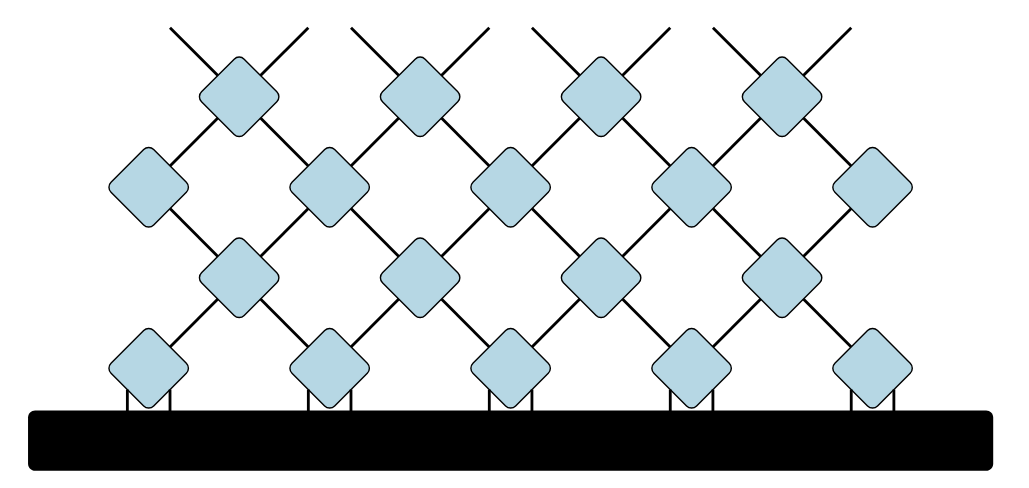 虚時間発展の様子
虚時間発展の様子
境界条件の掛け方こそ違いますが、45度回転すれば二次元イジング模型のダイアグラムと一致しています!そうなると、数式上も何かしら対応がありそうです。実際にみてみましょう。
先ほど2次元古典イジング模型を考えた時は上下と左右で相互作用が同じ大きさだとしましたが、今度は横方向は$J_x$、縦方向は$J_y$としてみましょう。1次元系の時のようにそれぞれのスピンが上下どちらかを考えて$2^4=16$個の要素で書き下してあげると、以下のようになります。
\begin{equation}
\begin{pmatrix}
e^{2\beta(J_x+J_y)} & 1 & 1 & e^{2\beta(-J_x+J_y)} \\
1 & e^{2\beta(J_x-J_y)} & e^{2\beta(-J_x-J_y)} & 1 \\
1 & e^{2\beta(-J_x-J_y)} & e^{2\beta(J_x-J_y)} & 1 \\
e^{2\beta(-J_x+J_y)} & 1 & 1 & e^{2\beta(J_x+J_y)} \\
\end{pmatrix}
\end{equation}
$J_x\gg J_y$の場合を考えます。上の系から$e^{2\beta J_x}$を括り出して、$e^{-2\beta J_x}$の項まで残すと
\begin{equation}
e^{2\beta J_x}\begin{pmatrix}
e^{2\beta J_y} & e^{-2\beta J_x} & e^{-2\beta J_x} & 0 \\
e^{-2\beta J_x} & e^{-2\beta J_y} & 0 & e^{-2\beta J_x} \\
e^{-2\beta J_x} & 0 & e^{-2\beta J_y} & e^{-2\beta J_x} \\
0 & e^{-2\beta J_x} & e^{-2\beta J_x} & e^{2\beta J_y} \\
\end{pmatrix}
\end{equation}
となります。また、異方的な古典イジング模型の相転移点は
\begin{equation}
\sinh(2\beta J_x)\sinh(2\beta J_y) = 1
\end{equation}
で与えられるので、極限
\begin{equation}
\begin{split}
\sinh(2\beta J_x)&\to e^{2\beta J_x}/2\\
\sinh(2\beta J_y)&\to 2\beta J_y
\end{split}
\end{equation}
を用いれば
\begin{equation}
\beta J_y=e^{-2\beta J_x}
\end{equation}
となります。これにより$e^{2\beta J_y}$の一次までは考慮に入れて
\begin{equation}
\begin{pmatrix}
1+2\beta J_y & e^{-2\beta J_x} & e^{-2\beta J_x} & 0 \\
e^{-2\beta J_x} & 1-2\beta J_y & 0 & e^{-2\beta J_x} \\
e^{-2\beta J_x} & 0 & 1-2\beta J_y & e^{-2\beta J_x} \\
0 & e^{-2\beta J_x} & e^{-2\beta J_x} & 1+2\beta J_y \\
\end{pmatrix}
\end{equation}
となります。これを2次元古典イジング模型の時の式と見比べれば
\begin{equation}
\begin{split}
2\beta J_y = J\Delta\tau\\
e^{-2\beta J_x} = \frac{h\Delta\tau}{2}
\end{split}
\end{equation}
となります。以上のプロセスから、虚時間発展演算子を用いることで、2次元古典系と1次元量子系を結びつけることができました!
まだまだ物語は続く...
いかがでしたでしょうか?簡単なイジング模型から初めて、テンソルネットワークのコンセプトと量子古典対応の描像を紹介していきました。一般に$n$次元の量子系と$n+1$次元の古典系を結びつけるこのような対応を量子古典対応と呼びます。この量子古典対応の考え方は単に量子系と古典系の対応関係というだけでなく、時空の対応関係にもなっているのが今までの議論から見えてきたのではないかなと思います。この考え方は後々重要になってきます。
次回はテンソルネットワークとくりこみをテーマに、実用的な計算手法を理解することを目指しながら、繰り込みとは何か、なぜテンソルネットワークが優れているのか、どのような仮定と精度の元で近似を入れていくのかなど、詳しくみていこうと思います。お楽しみに!
 またみてにゃ〜
またみてにゃ〜
