GL(n,C)の中心を表現論的に求める
$GL(n,\C)$の中心
問題
群の中心は次のように定義されます.
$G$を群とする.$G$の任意の元と可換な元全体
$$Z(G):=\{g\in G:\forall h\in G,gh=hg\}$$
を$G$の中心という.
群$G$の中心は$G$の部分Abel群になることが示されます.
$n\ge 1$とする.$n$次複素一般線型群
$$GL(n,\C):=\{A\in\operatorname{Mat}(n,\C):\det{A}\ne 0\}$$
の中心を求めよ.
$A\in Z(GL(n,\C))$であるとは,任意の正則行列$B$と可換,つまり$AB=BA$となることです.例えば$A=\lambda E_n$($E_n$:$n$次単位行列,$\lambda\in\C^{\times}=\C\setminus\{0\}$)であればこれを充たします.実はこの形で$Z(GL(n,\C))$の元は全て尽くされます.
$$Z(GL(n,\C))=\{\lambda E_n:\lambda\in\C^{\times}\}$$
計算によって示すこともできると思うのですが,今回はこれを表現論の強力な補題を用いて示します.
Schurの補題
係数体を$k$とします.
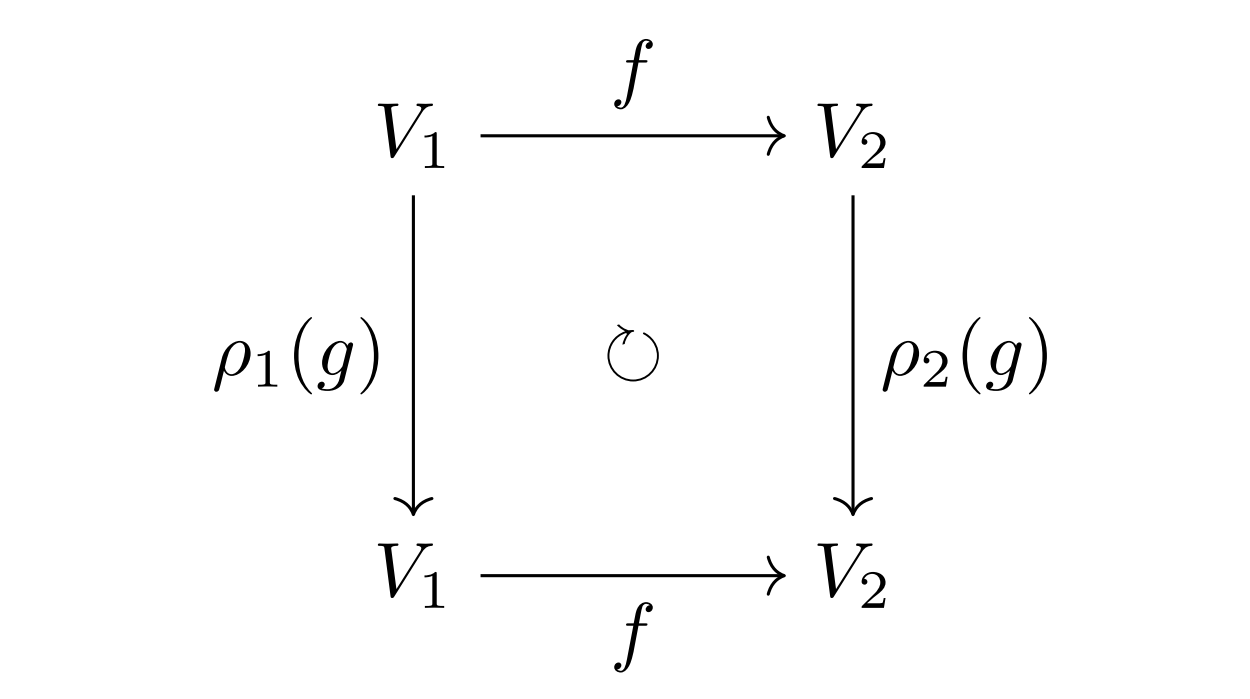
$(\rho_1,V_1),(\rho_2,V_2)$を群$G$の既約表現とする.$k$線型写像$f:V_1\to V_2$は,
\begin{align}
\forall g\in G,\ f\circ\rho_1(g)=\rho_2(g)\circ f \tag{a}
\end{align}
を充たすとする.(つまり$f$を$G$準同型とする.)このとき,$f=0$または$f$は線型同型である.
特に$k$が代数閉体,$(\rho_1,V_1),(\rho_2,V_2)$が有限次元既約表現であるとき,
\begin{align}
\exists \lambda\in k,\ f=\lambda\id \tag{b}
\end{align}
(a)は任意の$g\in G$に対して次の図式が可換になるという条件です.
命題1の証明
$G=GL(n,\C))$とおく.
$$\rho\colon G\to GL(\C^n),A\mapsto f_A$$
(但し$f_A\colon \C^n\to\C^n,x\mapsto Ax$)
とおくと,$(\rho,\C^n)$は既約表現になる.実際,任意の部分空間$W$と任意の$w\in W$に対して,適当な可逆変換によって$w$を$W$の外に出せるので不変部分空間は存在しないことが示される.
$A\in Z(G)$のとき,
$$\forall B\in G,AB=BA$$
つまり
$$\forall B\in G,\ f_A\circ\rho(B)=\rho(B)\circ f_A$$
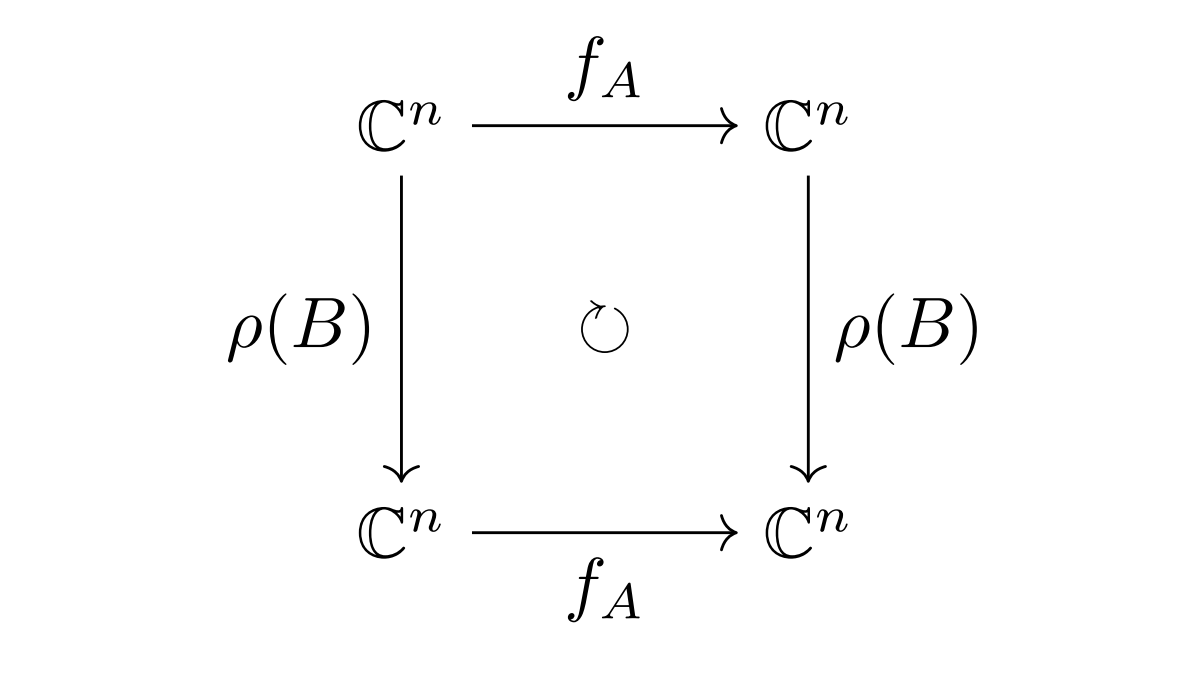
である.これと$\C$が代数閉であること及び$(\rho,\C^n)$が有限次元既約表現であることから,Schurの補題(b)により,
$$\exists\lambda\in\C,f_A=\lambda\id $$
つまり$A=\lambda E_n$とかける.$A$は正則なので$\lambda\ne 0$であるから,
$$Z(G)\subset\{\lambda E_n:\lambda\in\C^{\times}\}$$
がいえる.逆の包含は明らかなので結論
$$Z(GL(n,\C))=\{\lambda E_n:\lambda\in\C^{\times}\}$$
を得る.
Schurの補題がこのように利用されることが興味深いと思ったので記しました.執筆者はまだ表現論への理解が浅いため,もし誤りや補足などありましたらコメントにてご教授いただけますと助かります.
