Cartan–Dieudonné の定理(直交群は鏡映で生成される)
はじめに
Mathlog ユーザーのみなさん，はじめまして．初投稿なので緊張しています(テンプレ)．
今回は，直交群が鏡映で生成されること，そしてその応用として正規直交群が弧状連結であることを示します．
まずは用語確認から．
定義
直交群の定義についておさらいします．詳しいことは Google 先生に聞いてください．
$n$を正の整数とします．$\mathbb{R}$線形空間$\mathbb{R}^n$には標準的な内積
\begin{equation}
(x,y)=x_1y_1+\cdots+x_ny_n,\quad \text{for $x={}^t(x_1,\ldots,x_n),y={}^t(y_1,\ldots,y_n)$}
\end{equation}
が入っています．この内積を保つ自己同型$\mathbb{R}^n\to \mathbb{R}^n$全体のことを直交群というのでした．つまり、
\begin{equation}
\mathrm{O}(n)=\{A\in \mathrm{GL}_n(\mathbb{R})\mid (Ax,Ay)=(x,y)\quad \forall x,y\in\mathbb{R}^n\}
\end{equation}
です．
$\mathrm{O}(n)$は，行列の積に関して群をなすことがわかります．
直交群には，鏡映と呼ばれる特別な元が存在します．
$v\neq0\in\mathbb{R}^n$に関する鏡映とは，以下で定義される写像$r_v:\mathbb{R}^n\to\mathbb{R}^n$のことである．
\begin{equation}
r_v(x):=x-\frac{2(v,x)}{(v,v)}v,\quad x\in \mathbb{R}^n
\end{equation}
式の形から「$v$に関する折返し」という感じがするかと思います．
訂正(6/11)：$r_v$が「$v$に関する折返し」と口走りましたが，指摘があったように「$v$に直交する$n-1$次元超平面$(=v^\bot)$に関する折返し」が正しいです．「$v$に関する折返し」は鏡映$r_v$を用いて$-r_v$と表すことができます．一般には直交群の元は$-r_v$たちの積で書くことはできません(たとえば$n$が奇数のときは$-r_v$の行列式は$1$になってしまう)．ご指摘くださった方，ありがとうございます．
$r_v$が$\mathrm{O}(n)$の元であることを確認しておきましょう．
鏡映に関して次が成り立つ．
- $r_v$は線形写像である．
- $r_v\cdot r_v=\mathrm{id}_{\mathbb{R}^n}$である．とくに$r_v\in\mathrm{GL}_n(\mathbb{R})$である．
- $r_v$は内積$(\bullet,\bullet)$を保つ．よって$r_v\in\mathrm{O}(n)$である．
- $r_v$は$v$の生成する部分空間$\mathbb{R}v$上$-1$倍，$v$の直交補空間$v^\bot=\{w\in V\mid (v,w)=0\}$上恒等写像である．
この命題の4.は鏡映の折返しとしての性質をよく表していると思います．
どれも計算するだけ．
Cartan–Dieudonné の定理
先ほど，直交群の特別な元として鏡映を導入しました．実は，直交群の任意の元は鏡映の有限個の積で書けることが従います．
$n=2$の場合，このことは図形的かつ直感的に理解できます．すなわち，角度$\theta$の回転をしたかったら，まず$x$軸に関して折り返して，次に直線$y=(\tan(\theta/2))x$に関して折り返せばよいわけです(下図参照)．
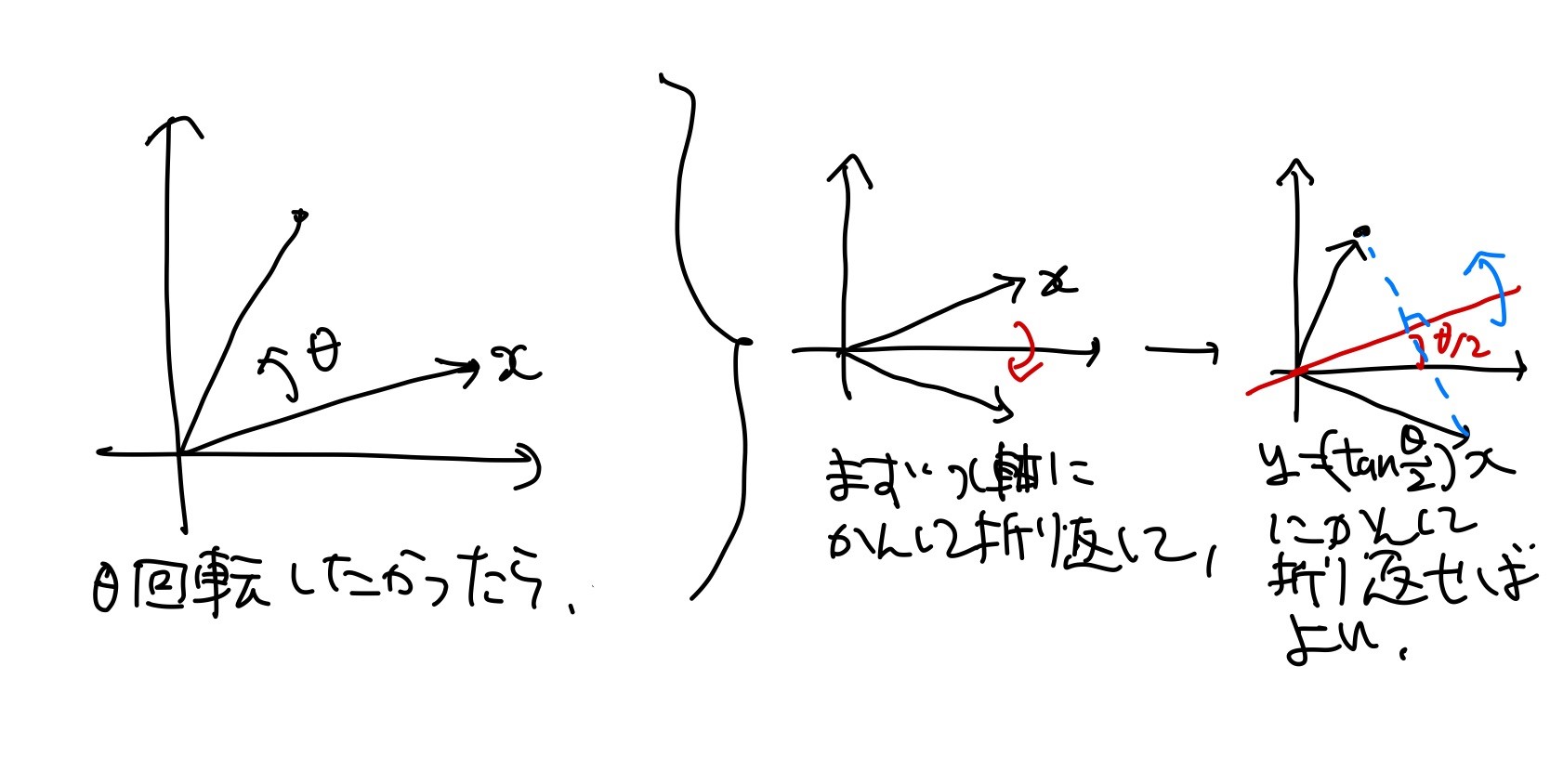2次元回転は鏡映の合成
$n$次直交群の元は，たかだか$n$個の鏡映の積で表される．
次元$n$に関する帰納法によります．方針としては，$A\in\mathrm{O}(n)$が与えられたとき，「$\text{(いくつかの鏡映の積)}\cdot A$」の形の元で，$e_n={}^t(0,\ldots,0,1)\in\mathbb{R}^n$を固定するものを探します．これを$B$とおくと，$B$は$e_n$の直交補空間，すなわち$\mathbb{R}^{n-1}$の直交群の元を引き起こすことがわかり，帰納法が使えます．では証明に移ります．
$n=1$の場合，$\mathrm{O}(n)=\{\pm1\}$の元はたかだか1個の鏡映の合成である．
以下$n>1,\ A\in\mathrm{O}(n)$とする．このとき，$B\in\mathrm{O}(n)$を以下で定める．
(i) $Ae_n=e_n$の場合，$B=A$とおく．
(ii) $Ae_n\neq e_n$の場合，$B=r_{Ae_n-e_n}\cdot A$とおく．
すると，いずれの場合も$Be_n=e_n$であることがわかる．実際，(i)の場合は明らかなので(ii)について考えればよいが，定義1によって計算すると
\begin{align}
Be_n&=r_{Ae_n-e_n}\cdot Ae_n\\
&=Ae_n-\frac{2(Ae_n-e_n,Ae_n)}{(Ae_n-e_n,Ae_n-e_n)}(Ae_n-e_n)\\
&=Ae_n-\frac{2\{(e_n,e_n)-(e_n,Ae_n)\}}{2\{(e_n,e_n)-(e_n,Ae_n)\}}(Ae_n-e_n)=e_n
\end{align}
となる($A\in\mathrm{O}(n)$が内積を保つことを用いて計算する)．
さて，$B$の$V:=e_n^\bot=\mathbb{R}^{n-1}\subset \mathbb{R}^n$への制限$B':=B|_{V}$が$\mathrm{O}(n-1)$の元を引き起こすことを見る．$\mathbb{R}^n$の内積$(\bullet,\bullet)$を$V$に制限したものは自然に$V$の内積とみなせることに注意する．いま，$Be_n=e_n$なので，任意の$x\in V=e_n^\bot$に対して
\begin{equation}
(e_n,Bx)=(Be_n,Bx)=(e_n,x)=0,
\end{equation}
よって$Bx\in V$である．つまり$BV\subset V$なので，$B$は$V$上の自己同型を引き起こす．すなわち$B'\in \mathrm{GL}_{n-1}(\mathbb{R})$．$B'$は$B\in\mathrm{O}(n)$の元の制限として与えられているのだから，明らかに内積を保つ．よって$B'\in\mathrm{O}(n-1)$である．
$n$に関する帰納法から，たかだか$n-1$個の元$v_1,\ldots,v_{m}\in V$があり，
\begin{equation}
B'=r_{v_1}\cdot\cdots\cdot r_{v_{m}}
\end{equation}
となる．$\mathbb{R}e_n$上では$B$と$r_{v_1}\cdot\cdots\cdot r_{v_{m}}$は共に恒等写像(命題1.4を参照)なので，結局$\mathbb{R}^n$上
\begin{equation}
B=r_{v_1}\cdot\cdots\cdot r_{v_{m}}
\end{equation}
となる($\mathbb{R}^n=\mathbb{R}e_n\oplus V$と分解されている)．(i)，(ii)のそれぞれの場合に応じて，
(i) $A=r_{v_1}\cdot\cdots\cdot r_{v_{m}}$
(ii) $A=r_{Ae_n-e_n}\cdot r_{v_1}\cdot\cdots\cdot r_{v_{m}}$
となる．以上で定理が示された．
お疲れ様でした．結構骨が折れますね．
応用：特殊直交群は連結である
以下$n\times n$行列全体の空間$\mathrm{M}_{n}(\mathbb{R})$を Euclid 空間$\mathbb{R}^{n^2}$と同一視することで位相を与え，$\mathrm{GL}_n(\mathbb{R})$や$\mathrm{O}(n)$にはその相対位相を考えるものとします．このとき$\mathrm{O}(n)$の連結性が気になります．
まず簡単にわかるように，$\mathrm{O}(n)$は連結ではありません．実際，$\det:\mathrm{M}_n(\mathbb{R})\to \mathbb{R}$を行列式として
\begin{equation}
\mathrm{O}(n)=(\mathrm{O}(n)\cap \det{}^{-1}(\mathbb{R}_{>0}))\cup(\mathrm{O}(n)\cap \det{}^{-1}(\mathbb{R}_{<0}))
\end{equation}
は空でない開集合による分割を与えます．ここで気になるのは，右辺に現れる
\begin{equation}
\mathrm{SO}(n):=\mathrm{O}(n)\cap \det{}^{-1}(\mathbb{R}_{>0})
\end{equation}
が連結かということです($\mathrm{SO}(n)$を特殊直交群と呼びます)．実は次が成り立ちます．
特殊直交群$\mathrm{SO}(n)$は(弧状)連結である．
任意の$A\in\mathrm{SO}(n)$と単位行列$1$が弧状連結であることを示せばよい．Cartan–Dieudonné の定理より$A\in\mathrm{SO}(n)$は有限個の鏡映の合成で書けるのだった．とくに$A$は偶数個の鏡映の積になる．それを示すには，鏡映の行列式が負であることを示せばよいが，これは命題1.4より従う．そこで
\begin{equation}
A=r_{v_1}\cdot\cdots\cdot r_{v_{2k}},\quad v_1,\ldots,v_{2k}\in\mathbb{{R}}^n\setminus\{0\}
\end{equation}
と書いてみる．$v_1,\ldots,v_{2k}$のいずれとも向きが異なる$w\in\mathbb{R}^n$を取り，$t\in[0,1]$に対して
\begin{equation}
A_t:=r_{(1-t)v_1+tw}\cdot\cdots\cdot r_{(1-t)v_{2k}+tw}\in \mathrm{SO}(n)
\end{equation}
とおく．$w$の取り方から任意の$i$と$t$で$(1-t)v_i+tw\neq0$なので well-defined である．これが$\mathrm{SO}(n)$内で$A$と$1$を結ぶ path を与える($A_1$は$w$に関する鏡映の偶数個の積なので恒等写像)．なお，$A_t$の連続性については，写像$\mathbb{R}^n\setminus\{0\}\ni v\mapsto r_v\in \mathrm{O}(n)$が連続であることを示せばよいが，これは$r_v$の第$i$列が標準基底$e_1,\ldots,e_n$を用いて
\begin{equation}
r_v(e_i)=e_i-\frac{2(e_i,v)}{(v,v)}v
\end{equation}
で与えられ，これは明らかに$v$に関して連続であることから従う．
おわりに
最後まで読んでいただいてありがとうございます．はじめての投稿であり，数学の文章を書くことにも慣れていないので読みづらいところも多いと思います(中の人は執筆当時 B3 のしがない数学系学生です)．
ちなみに定理2,3は去年の代数学の演習授業で出題されたものであり，ぼくは定理2(をより一般的な設定にしたもの)を証明する問題を解き，発表しました．同じ方法で証明している文献を見たことがないので，もし知っている人がいれば教えてください．
これからも面白いと思ったことについてつれづれなるままに書いていきたいと思いますので，どうぞよろしくお願いします．いまは力学系理論に興味があっていろいろ勉強しているので，次はそれについて書きたいですね．