星状領域は弧状連結

どうも

　こんにちは　ごてという者です　一発ネタ記事を書きたくなったので、書きます　証明のトレーニングにどうぞ（？）

星状領域の定義

　星状領域$S\subset {\mathbb{R}}^n$とは 何か点$x\in S$が存在して, $S$内の任意の点$y$とを結んだ線分が$S$に含まれる集合のことです.

　例は次のような感じです. わかりやすく${\mathbb{R}}^2$で考えます.

点を$x$で置いたのに$xy$平面で書いちゃった......ミスです

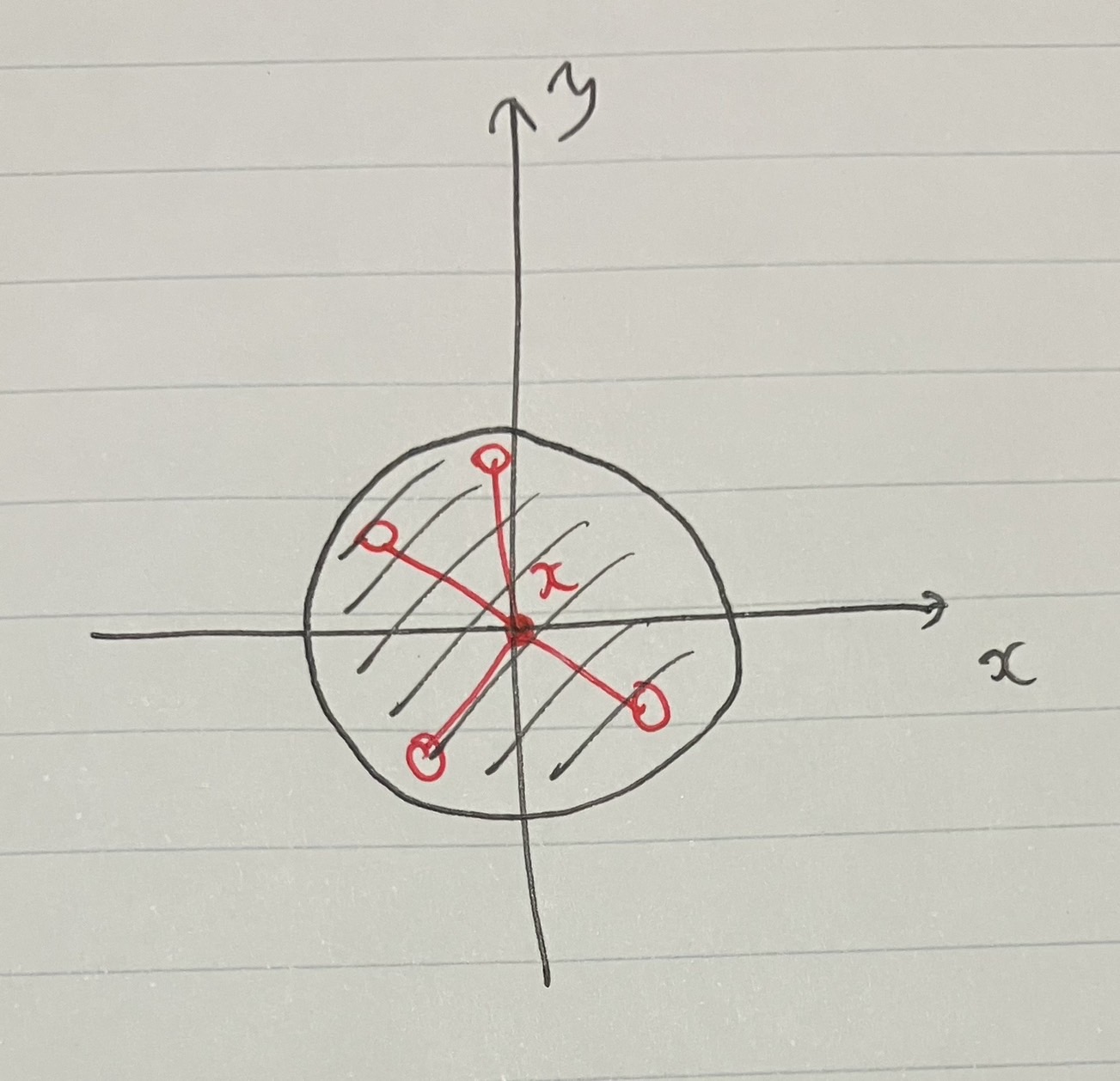円盤、定義上は星状

　こういうのは成り立たない例を見るといいと聞くので, 成り立たなそうな例も貼ります.

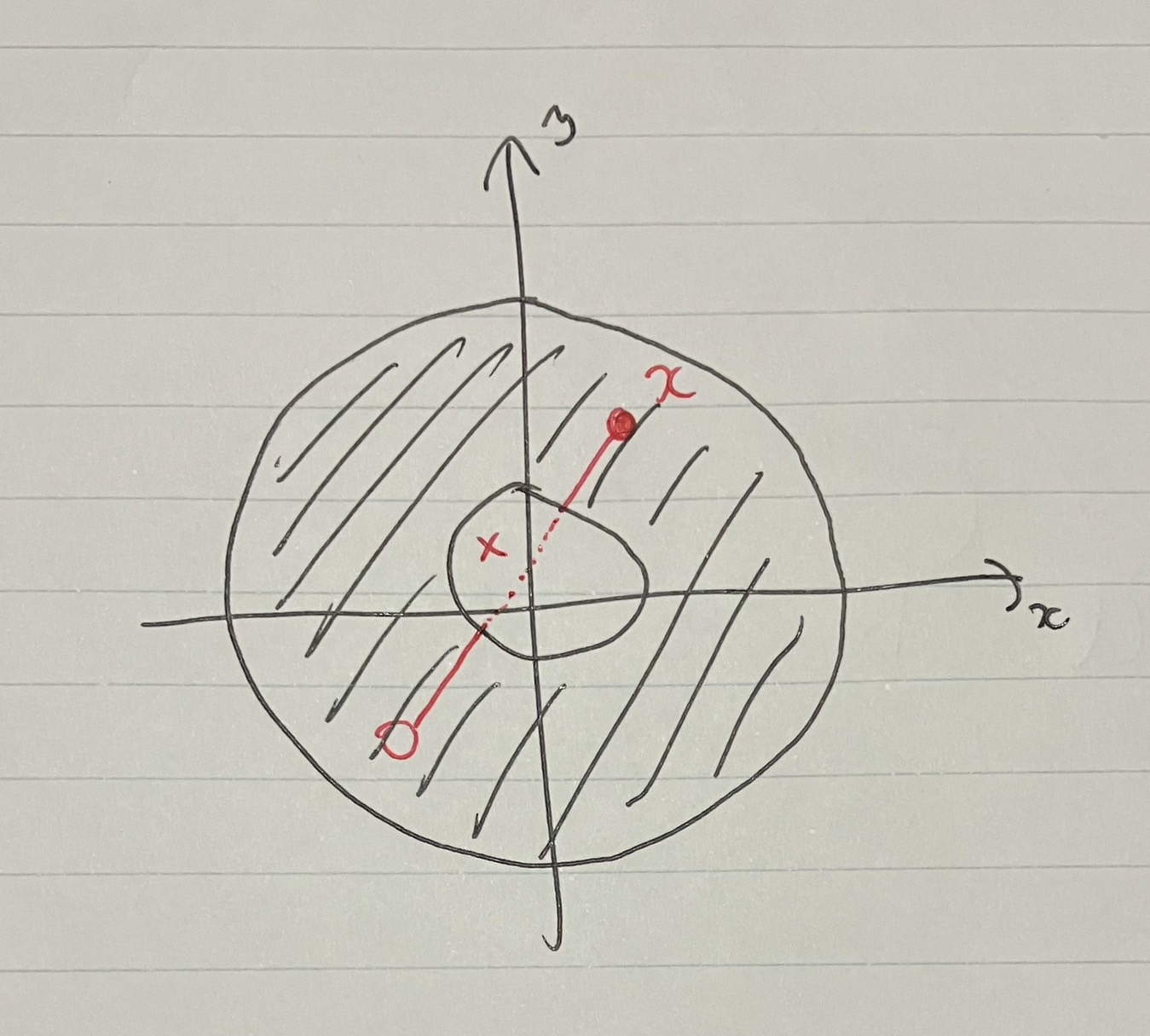これは星状じゃない

さて問題

　問題です. 考えてみてください！ 弧状連結の定義は調べてください（投）

　↓

　↓

　↓　答えは下

　↓

　↓

　↓

　↓

　↓

　↓

　↓

　↓

　↓

　↓

　↓

　↓

　↓

　↓

　↓

おわり

　ここまで読んでいただきありがとうございました　連結最高！